几何寻道 图形模型最相宜
——由一道向量竞赛试题引出的思考
● (开化中学,浙江 开化 324300)
2017-07-09
李承法(1969-),男,浙江开化人,中学高级教师.研究方向数学教育.
几何寻道图形模型最相宜
——由一道向量竞赛试题引出的思考
●李承法
(开化中学,浙江 开化 324300)
近年来,含有条件c=λa+μb(其中λ,μ∈R,λ+μ=1)的这类平面向量问题在高考卷、竞赛卷以及高考模拟卷中屡屡出现.这类试题常考常新,造成很多学生对此类试题无法应对.文章提出解决此类试题的关键在于运用向量“数”和“形”的属性,构造三点共线图形模型,运用数形结合思想可以有效求解.
平面向量;三点共线;数形结合
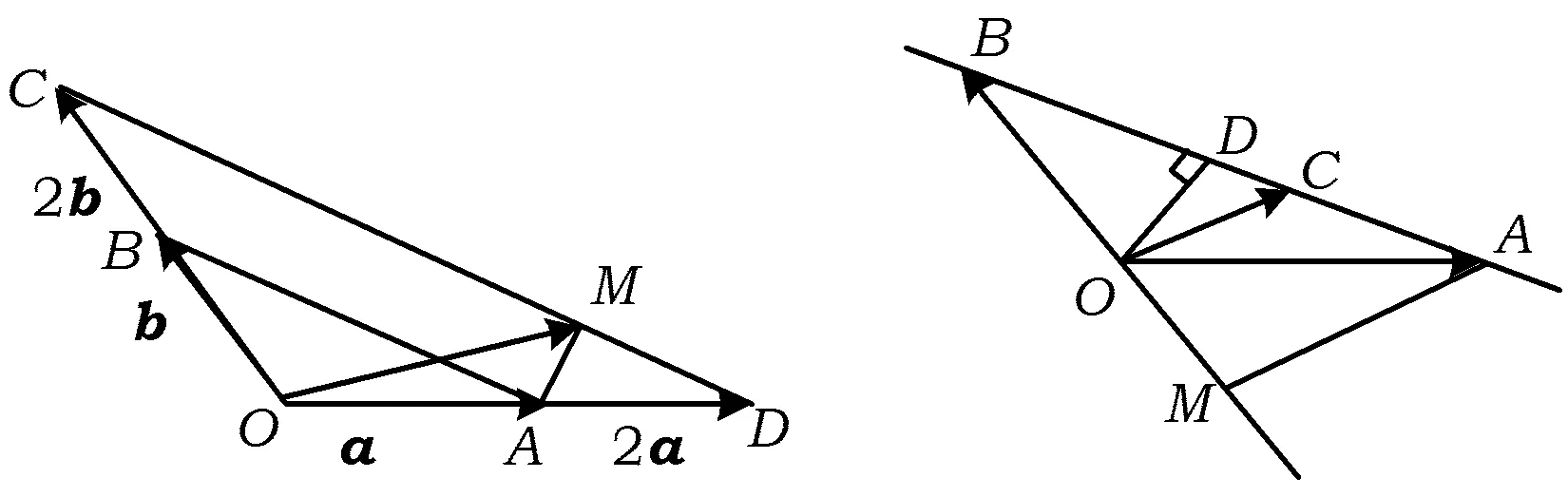
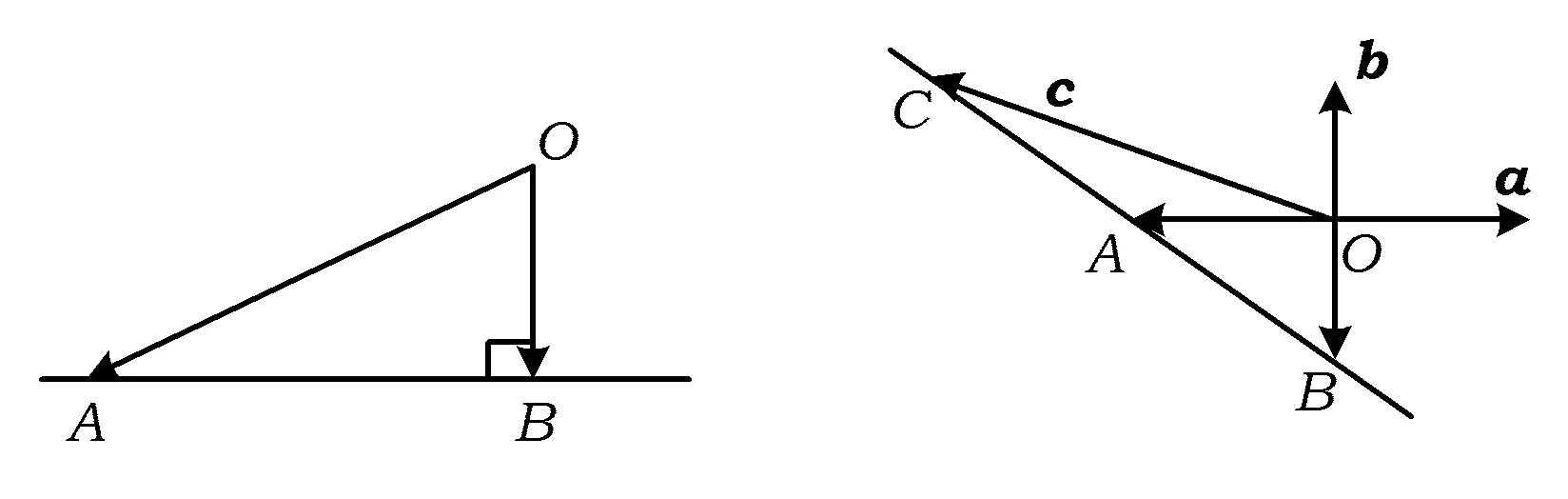
1 一个常用结论和图形模型
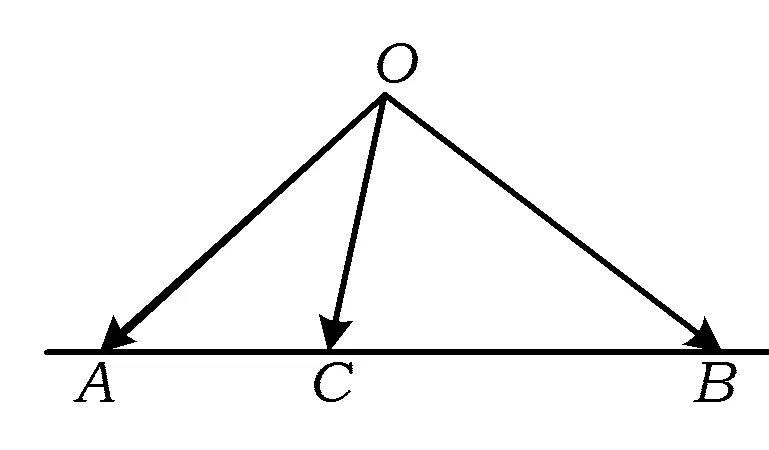
图1

2 问题的引出和解析
例1已知平面向量a,b,c,满足|a|=1,|b|=2,|c|=3(其中0<λ<1),若b·c=0,则|a-λb-(1-λ)c|所有取不到的值的集合为______.
(2017年浙江省高中数学竞赛试题第9题)
解法1将向量b,c的起点平移至原点O,再分别以b,c为x,y轴正向建立平面直角坐标系,则向量b=(2,0),c=(0,3),向量λb+(1-λ)c对应的点坐标为P(2λ,3(1-λ)),从而
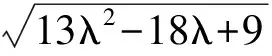
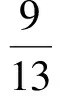
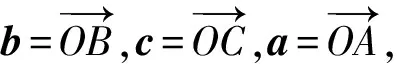
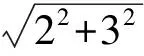

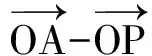
点A在单位圆(即⊙O)上运动,从而当AP⊥BC时(如图2),|a-λb-(1-λ)c|取到最小值
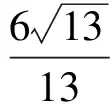
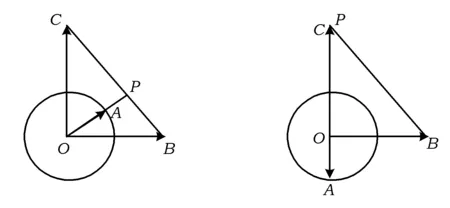
图2 图3
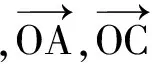
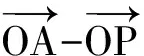
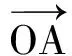
而0<λ<1,点P与点C不重合,于是
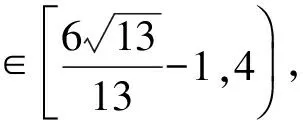


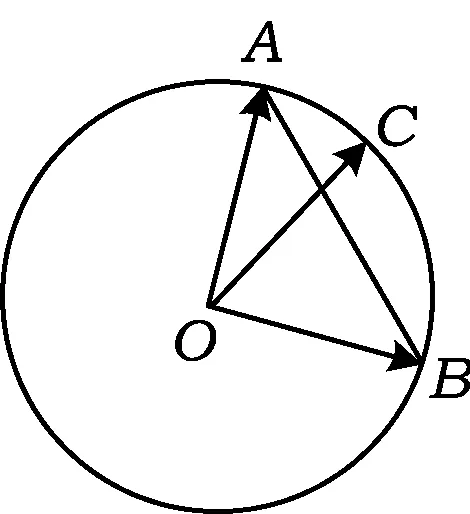
图4
2.1 同类试题的解决

( )
A.0
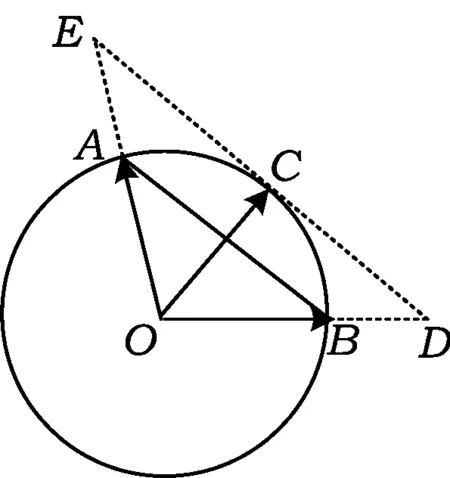
C.m+n<-1 D.-1 (2014年浙江省高一数学竞赛预赛第一试第8题) 分析因为线段OC与线段AB交于圆内一点,不妨设为点P,则由向量基本定理中的三点共线结论可知 且 λ1+λ2=1. m=λλ1,n=λλ2, 因此 m+n=λ(λ1+λ2)=λ>1. 故选B. ( ) (2017年4月湖州、衢州、丽水三地市高三数学教学质量检测卷第9题) 图5 2.2 试题变式的归纳总结与延伸 笔者发现,例1是以平面向量基本定理为背景的题目,应用前面的结论和图形模型可以解决,而且这道题还能一般化,即当∠AOB=α(其中α为定角且α≠kπ,k∈Z)时,还能确定m+n的取值范围. 图6 sinθ=msinα, 且 cosθ=mcosα+n, 即 图7 且λ1+λ2=1.因为△OAB∽△ODE,由相似比得 进而 m=cλ1,n=cλ2, 因此 m+n=c, |OP|<1, 则 m+n>1, 限于篇幅,证明从略. (2011年重庆市第一中学高三数学模拟试题第10题改编) 图8 图9 (2013年浙江省杭州市高三一模数学试题第16题) 评注本题主要运用了三点共线、定理1和图形模型. ( ) (2017年浙江省余杭、长兴、缙云三校4月高考模拟试题第8题) 分析如图10,易知 同理可得 故选C. 图10 图11 图12 图13 变式3若a,b为平面内两个互相垂直的单位向量,若向量c满足c+a=λ(c+b)(其中λ∈R),则|c|的最小值为______. 分析c+a=λ(c+b)(其中λ∈R),即 向量复习中要加强数学语言、向量相关概念的理解,特别是试题中的向量等式表达形式如c=λa+μb(其中λ,μ∈R,λ+μ=1)表示三点共线、不等式形式意义的理解,运用图式(几何法)则要求我们在复习备考时要掌握基本图形模型,理解题目的几何属性、数图结合,追求理解几何实质,施行向量的相关线性运算转化求解策略,这在应试中尤为重要.教师复习教学时要指导学生重视整理:1)基本概念、定理、向量运算特别是数量积及其几何意义;2)主要的思想方法技巧;3)重要的图形背景(如平行四边形法则、图式模型)[3]. 另外,高三数学教师要关注每年的数学竞赛题,特别是向量试题,它的变式或同类题往往成为当年或今后高考题的前生.每年浙江省数学高考卷中的向量试题是全卷的亮点之一,它通常都是前几年数学竞赛向量题的演变,因此它就成了既新颖又蕴含思想立意的靓题了. [1] 章建跃.让学生在几何学习中学会认识和解决问题的方法[J].中学数学教学参考:中旬,2013(1/2):3-6. [2] 李承法.向量问题的几种图形模型[J].中学数学月刊,2015(10):46-47. [3] 周荣阳.“变”中找“定”——浅析平面向量几何法[J].中学教研(数学),2014(10):32-34. O123.1 A 1003-6407(2017)10-47-04


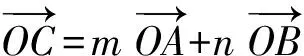
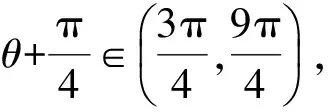

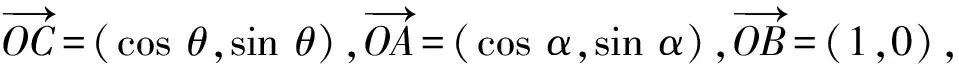
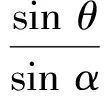
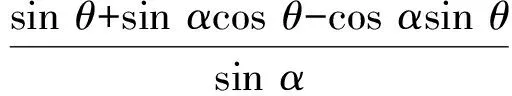
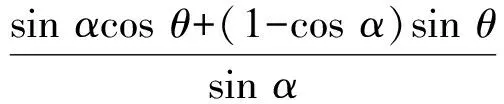
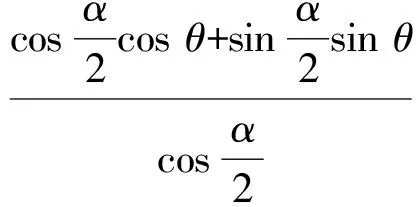
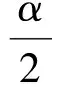
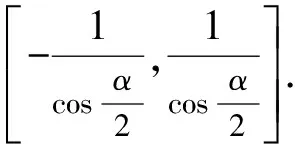
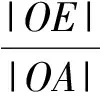


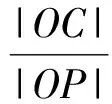


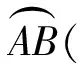
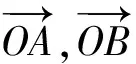
3 例题与变式研究
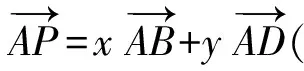
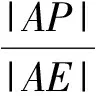

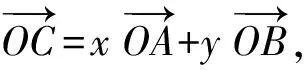
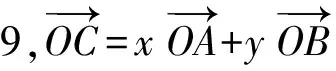
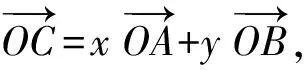
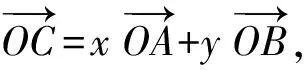
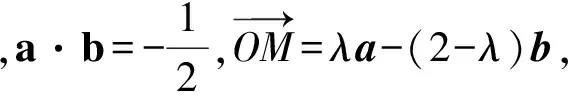

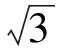
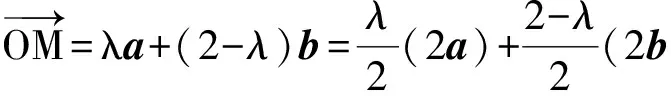


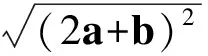
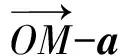


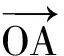
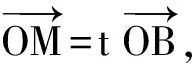
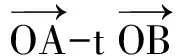
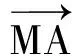
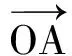
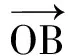
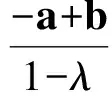
4 向量问题应试策略

