清风和雨 绵绵悠长——2017年高考数学文化试题感悟

● (英雄山中学,山东 泰安 271000)

2017-08-01

尹承利(1963-)，男，山东泰安人，中学高级教师.研究方向数学教育.

清风和雨绵绵悠长
——2017年高考数学文化试题感悟

●尹承利
(英雄山中学,山东 泰安 271000)

教育部考试中心下发的《关于2017年普通高考考试大纲修订内容的通知》(教试中心函(2016)179号)，公布了2017年各学科高考大纲的主要修订内容，在数学考纲的修改部分，特别强调了要对数学文化进行考查.“数学文化怎样考”成为中学数学界热议和期待的话题，2017年高考对“数学文化”的考查是以怎样的面目呈现的？文章就此作一些赏析和感悟.

高考;数学文化;感悟

2017年高考对“数学文化”的考查，虽然没有呈现出人们预期的“骤风大作”的气势，倒也“清风和雨”润人心田.在高考试题中渗透数学文化成为2017年数学高考“可圈可点”的一大亮点，全国卷Ⅰ、卷Ⅱ和高考改革地区的浙江卷都作了有益的尝试与探索，体现了高考“增加数学文化”的要求.

1 试题赏析

例1我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增；共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯

( )

A.1盏 B.3盏 C.5盏 D.9盏

(2017年全国数学高考卷Ⅱ理科试题第3题)

分析可设最顶层灯塔所挂灯数为a，则第2层为2a，第3层为4a，…,第7层为64a.本题实质是考查等比数列求和公式，从而127a=381，可得a=3.故选B.

评注我国古代数学有着极其辉煌的成就，出现过刘徽、祖冲之、秦九韶、杨辉等伟大的数学家，以及《九章算术》、《数书九章》、《算数书》、祖暅原理等数学名著和名题.以这些名著、名题为试题背景，可以引导我们理解数学，感受数学家的崇高品质及探究、解决数学问题的过程，进而体会中国古代数学的伟大贡献，增强爱国主义情怀.程大位是我国明代伟大的数学家，被誉为“珠算之父”，他的应用数学巨著《算法统宗》的问世，标志着我国的算法由筹算到珠算转变的完成.程大位在《算法统宗》中常以诗歌的形式呈现数学问题，体现了数学的“文化美”.

例2我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”，将π的值精确到小数点后7位，其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内接正六边形的面积S6，S6=________.

(2017年浙江省数学高考试题第11题)

分析将正六边形分割为6个等边三角形，则

评注割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周长和面积越来越接近于圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”．刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率π的近似值.说到圆周率π，自然想到我们引以为豪的“徽率”和“祖率”，它的历史饶有趣味,我国古代数学家对圆周率方面的研究工作，成绩十分地突出.本题所介绍的祖冲之研究圆周率π的成果，让我们感到无比自豪和骄傲，古代科学家在艰难的环境中研究科学的无私精神和崇高品质，值得我们尊敬和学习.

例3如图1，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是

( )

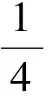
(2017年全国数学高考卷Ⅰ文科试题第2题)

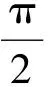
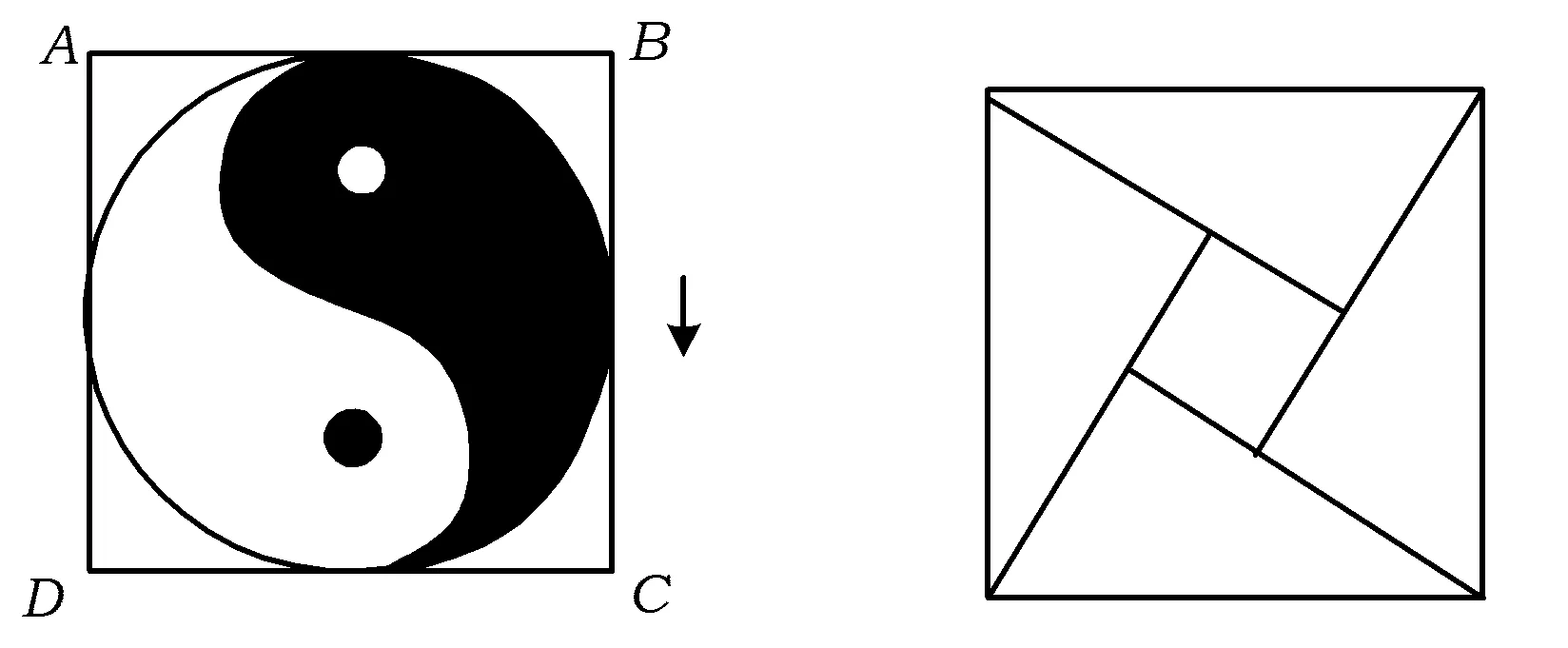
图1 图2

评注在我国传统文化中有很多体现“数学美”的图形.如本题所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分体现了相互转化、对称统一的形式美、和谐美.还有像庄重大气的2002年北京国际数学家大会的会标，它是以“赵爽弦图”为基础设计的.勾股定理是刻画直角三角形特征的一条重要定理，它的发现、验证、应用蕴含着丰富的文化价值，最早对勾股定理进行证明的是1700多年前的汉代数学家赵爽，他绘制了极富创意的弦图，后人称之为“赵爽弦图”(图2)，采用“出入相补”原理使得勾股定理不证自明.以“弦图”为基本图形，定理的证明体现了“形数统一”的思想方法，具有科学创新的重大意义.我国数学文化中蕴含着丰富的宝藏，值得我们去深入挖掘.

2 3点感悟

2.1 高考试题体现了“3个渗透”

数学文化的最主要内涵是一种理性思维方式在实践过程中的不断探索，形成的数学史、数学精神及其应用[1].2017年的高考“数学文化”试题基本体现出了“3个渗透”——渗透数学史料、渗透数学精神、渗透数学应用.上述3个高考试题所渗透的数学史料，让我们自然而然地接受了“数学文化”的熏陶；古代数学家刘徽、祖冲之及祖暅在艰难困苦的环境中研究科学的数学精神值得我们学习和敬仰，也更增加了我们的爱国情怀；我国古代数学遵循“经世济用”，涉及的研究大多与实际生活、生产结合紧密，具有浓厚的实际背景，无论是例1还是例2都充分说明了这一点.

2.2 高考试题起到了导向作用

数学文化是数学学科的一个有机组成部分，有着非常丰富的内涵和外延.了解数学文化，有利于激发学生对于数学学习的欲望和兴趣.在高考试题中渗透数学文化，可以适当引导中学数学的教学，使得更多的教师关注数学文化，研究数学文化，将数学的本质教授给学生.学生通过数学文化的熏陶，可以促进对健全人格的养成.一方面，可以学到了数学家们那种不畏艰辛、不怕失败的精神；另一方面，又能学到以退为进、逐步调整的方法和策略，形成了能进能退的开阔胸襟.这正是一种文化的迁移，一种文化的教育[1].2017年的“数学文化”试题对中学的教与学起到了基本导向和引领作用.

2.3 高考考查数学文化的长期性

在数学高考中加强数学文化的考查，旨在发挥高考“指挥棒”的作用，通过考题让学生感受中国的传统文化之美并予以传承.这不是一蹴而就的事情，是一个长期的过程.其实，不仅是2017年的高考，即使在前几年的全国数学高考新课标卷和湖北卷等已有了大胆的尝试，比如：2015年全国数学高考新课标卷Ⅰ文、理科第6题都考查了《九章算术》中的“委米依垣”问题、2015年全国数学高考新课标卷Ⅱ文、理科第8题考查了《九章算术》中的“更相减损术”、2016年全国数学高考新课标卷Ⅱ理科第8题考查了“秦九韶算法”等.

因此，在数学教与学中，要充分重视对“数学文化”的学习渗透，特别是要有的放矢地将现行人教版《普通高中课程标准试验教科书·数学》中“数学文化”的典型案例，如必修1中的阅读材料“中外历史上的方程求解”；必修2中的探究与发现材料“祖暅原理与柱体、锥体、球体的体积”；必修3算法案例中的“秦九韶算法、更相减损术及割圆术”；必修5中的阅读材料“海伦和秦九韶”“九连环”；选修2-3中的探究与发现材料“‘杨辉三角’中的一些秘密”等学习到位并予以拓展，从而促进学生理性思维的发展.

[1] 陈昂，任子朝．突出理性思维 弘扬数学文化[J]．中国考试，2015(3):10-14．

O119

A

1003-6407(2017)10-45-02