素养本天成 向量妙显之——基于2017年浙江省数学高考试题第15题

● (平湖中学,浙江 平湖 314200)

2017-07-22

李学军(1976-)，男，吉林德惠人，中学高级教师.研究方向数学教育.

素养本天成向量妙显之
——基于2017年浙江省数学高考试题第15题

●李学军曲文瑞
(平湖中学,浙江 平湖 314200)

数学教师要研究学生的解题，引导学生用数学的眼光观察问题，用数学的思维进行思考和解决问题，去体会、体验在解题过程中的纠结和成功之后的快乐，实现真正意义的数学学习.文章结合2017年浙江省数学高考试卷中的一道填空题，深入挖掘考点，深刻探寻题源，进而享受2017年浙江省数学高考文理合卷的经典美.

浙江考题;解法探究;教学启迪

2017年的高考已经落下帷幕，2017年是浙江省高考改革数学文理合卷的第一年，根据以往文科生和理科生的思维特点，浙江省考试院完善了往届的考试说明，出台了《2017年浙江省普通高中高考考试说明》.2017年的高考试卷严格按照新的考试说明及学科指导意见进行命制，关注学生数学基础及必备数学问题解决能力的考核，强调数学知识的基础性、能力应用的综合性，真正体现了《数学课程标准》中提到的“使学生掌握数学的基础知识、基本技能、基本思想，使学生表达清晰、思考有条理，使学生具有实事求是的态度、锲而不舍的精神，使学生学会用数学的思考方式解决问题、认识世界.”

1 去年今日此门中——考题重现

题目已知向量a,b满足|a|=1，|b|=2,则|a+b|+|a-b|的最小值是______，最大值是______.

(2017年浙江省数学高考试题第15题)

本题作为填空题的第5题(填空题共7题)，在填空题中处于关键性的位置，起到承上启下的作用，同时根据往届文科考生和理科考生的特点命制这样一道具有分水岭的漂亮的向量考题，能够快速考查出数学思维高、素养深的学生；对于数学水平一般的学生通过对问题的分析理解，从问题的概念入手，运用常规方法依然能够达到自己理想的结论.教材《数学(必修4)》第109页的例1就是探究平行四边形的4条边与两条对角线之间的关系问题.本题紧扣教材，无论是函数值范围的处理还是数形结合的数学思想都源于教材.该题作为填空题的关键性试题语言简洁，解题入口宽、层次多、区分度好，具有非常明显的“浙江风彩”.

2 人面桃花相映红——解法探究

视角1坐标的视角

分析设a=(cosα,sinα)，b=(2,0),则

|a+b|+|a-b|=

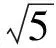
点评利用坐标法解决平面向量问题，实际上就是把抽象的向量问题转化为坐标运算.不同的学生建立的平面直角坐标系可能不同，但是对于解决该题影响并不大，关键是转化为以角为自变量后的函数最值的处理.通过观察可以发现两个根号内部的变量之间是互为相反数的，因此，平方处理是比较理想的处理方式.

视角2基底的视角

分析设=α∈[0,π]，则

|a+b|+ |a-b|=

以下解答同视角1.

点评平面向量基本定理是平面向量知识中非常重要的一个知识点.易知向量a,b是非常恰当的一组基底(当a,b不共线时)，只要确定a,b的夹角,|a+b|+|a-b|就可以用夹角进行表示，通过引入向量的夹角，问题的难点便得到很好地转化.

视角3规划的视角

分析设|a+b|=x,|a-b|=y,其中x,y≥1,则

x2+y2=|a+b|2+|a-b|2=10，

图1

原问题转化为“已知x2+y2=10(其中x≥1,y≥1)，求x+y的最大值及最小值”.

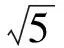
点评该方法的关键是换元，通过换元找出两个变元x,y之间的等量关系，通过分析得出变元x,y的范围，从而得出轨迹是圆的一部分.而要研究的结论恰好和直线的截距有关，利用数形结合比较容易得出结论.

视角4根的分布视角

分析由视角3可知，原问题可转化为“已知x2+y2=10(其中x≥1,y≥1)，求x+y的最大值及最小值”.

图2

2x2-2tx+t2-10=0.

由题意知方程2x2-2tx+t2-10=0在[1,3]内有两个根.

设f(x)=2x2-2tx+t2-10,如图2所示得

解得

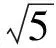
点评该方法的关键是发现等式中的二次关系，还有一个一次关系.两个方程、3个变量，通过消元得到以x为主元的一元二次方程，方程的根的范围可以确定，利用根的分布解决问题应是顺理成章的，但是在考场上要通过两次转换，并且要解4个不等式，对于小题目来说，不应该成为主流.

视角5三角换元的视角

分析由视角3可知，原问题可转化为“已知x2+y2=10(其中x≥1,y≥1)，求x+y的最大值及最小值”.

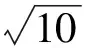
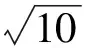
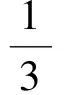
点评该方法来源于三角函数的定义，实质是引进新的变元，把x,y用新的变元表示，把新的变元作为主元，找出主元的取值范围，从而转化为函数问题进行处理.也可以通过平方，转换为齐次式，以tanα为主元进行处理，这也是一种非常漂亮的方法.

视角6构造的视角

分析设a=(1,0)，则

-a=(-1,0),b=(2cosα,2sinα).

图3

如图3，设点A(1,0),A′(-1,0),B(2cosα,2sinα),则

|a+b|+ |a-b|=

|BA′|+|BA|,

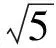
点评该方法的关键是从两个绝对值入手.绝对值的几何意义就是距离问题，通过引进坐标，转化为一个动点到两个定点的距离和的最值问题.转化之后可以发现，这刚好是椭圆的定义，进而求动态椭圆的长轴长的最值问题，通过观察即可得到想要的结果.该方法应该是此问题最本质的考查.

视角7几何的视角

分析如图4，设a=(cosα,sinα)，则

b=(2,0). -b=(-2,0),

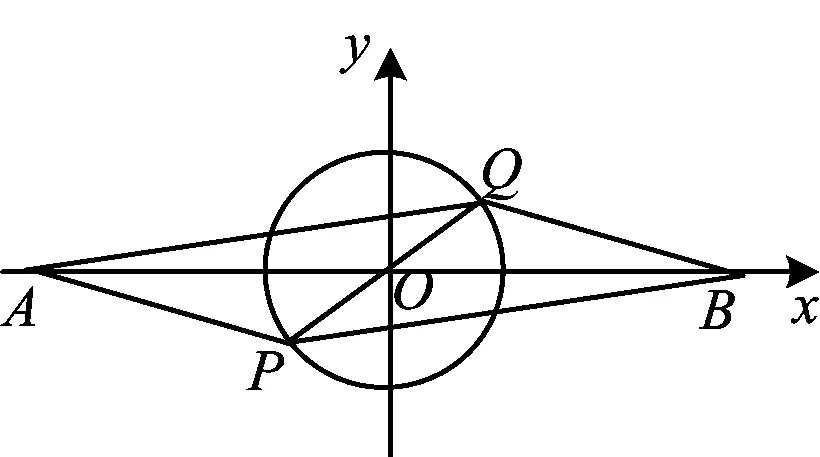
图4

设点B(2,0),A(-2,0),P(cosα,sinα),则点Q在圆x2+y2=1上,从而

|a+b|+ |a-b|=

|QA|+|QB|,

当点A,Q,B共线时，|a+b|+|a-b|取得最小值4.

点评该方法同视角6类似，转化为动点到两个定点的距离和，当3个点共线时，距离和最小.但是通过几何图形寻找最大值有一定难度.

视角8不等式的视角

分析平行四边形的两条对角线及4条边有如下关系：平行四边形的两条对角线的平方和等于4条边的平方和.特殊情况：当四点共线时仍然成立.

设|a+b|=x,|a-b|=y，其中x≥1,y≥1，则

x2+y2=10(其中x≥1,y≥1)，

从而

(x+y)2≤2(x2+y2)=20，

点评这个平行四边形的结论是教材中的例题，同时也是非常重要的结论，在例题的探究过程中还可以得出极化恒等式.已知平方和为定值，求两个正数的和的最大值，恰好可以构造基本不等式的变形公式或者柯西不等式，但用不等式求最小值对学生的能力又提出了新的考验.

3 人面不知何处去——源题追溯

源头1已知实数a,b,c满足a+b+c=0，a2+b2+c2=1，则a的最大值为______.

(2014年浙江省数学高考文科试题第16题)

( )

A.min{|a+b|,|a-b|}≤min{|a|,|b|}

B.min{|a+b|,|a-b|}≥min{|a|,|b|}

C.max{|a+b|2,|a-b|2}≤|a|2+|b|2

D.max{|a+b|2,|a-b|2}≥|a|2+|b|2

(2014年浙江省数学高考理科试题第8题)

源头3若实数x,y满足x2+y2≤1，则|2x+y-2|+|6-x-3y|的最小值是______.

(2015年浙江省数学高考理科试题第14题)

源头4已知平面向量a，b，|a|=1,|b|=2,a·b=1.若e为平面的单位向量，则|a·e|+|b·e|的最大值是______.

(2016年浙江省数学高考文科试题第15题)

4 桃花依旧笑春风——教学启迪

一道精彩的高考试题在一定程度上能够指导教师根据学生驾驭知识的实际情况，调整教学内容以及根据教学内容选择恰当的教学手段和方法，进而直接影响学生的数学学习能力的提升.这道平面向量填空题作为试卷中的关键性题目，虽然有着“入手易，解法多”的特点，但是在操作的过程中，有部分学生仍然有力不从心的感觉[1].因此，在平时的教学中我们应该更多关注以下几个方面：

4.1 关注基础，重视本质

张奠宙教授曾经说过：“数学教学的有效性关键在于对数学本质的把握、揭示和体验.”

在2017年浙江省数学高考试卷中，对知识的概念考查、对问题的本质考查贯穿于整张试卷，应该说是考查的重点.学生学习数学知识是从认识起步到理解、掌握，并在这个过程中逐渐清晰数学知识的本质，同时形成数学思想，培养数学思维[2].正如章建跃先生曾说过：“要让学生养成‘回到概念去’思考和解决问题的习惯.”我们平时所说的中档题目或者难题就是多个知识点进行交叉和互融的考核，因此，无论是新授课还是专题课的教学都应该从基础出发，在平时的教学中要尽量留给学生足够的时间读题、审题，在这个过程中读出若干个思维角度，审出题目的结构，理解问题的本质，这才是数学学习的根基所在.

4.2 强化通法，渗透巧法

高考是选拔性考试，既要保证考生在考场上走好寻常路，同时又要让那些有创造性的考生能够脱颖而出，因此在试题的设置上表现为“通性通法”重点考查.学生在考试的过程中，不同的学生对不同的知识理解是有差异的，数学素养比较高的学生会把多种通法综合到一起，从而创造出含有“技巧性元素”的方法.因此，在平时的教学中，要求教师更加注重对知识的“通性通法”的教学.只要对问题解决的通性通法过关、熟练、高效，某些试题的技巧性方法自然就会应运而生.解决问题的通法就是把握数学的学科思维特征，遵循数学的思维特征看待问题、分析问题和解决问题.

4.3 加强探究，提升素养

解题是一种创造性的活动，是理论到实践的过程.通过学生解题的过程可以发现：有一些题目的类似题或者原题已经教了许多遍，但是学生还是不能很好地掌握.因此，在教学中教师要敢于等待学生，陪伴学生重筑数学知识的形成之路，而不是在某些经典的知识点或者试题上“一滑而过”.正如波利亚曾形象地指出：“好问题同某些蘑菇有些相似，它们大都成堆的生长，找到一个之后，你应当在周围再找一找，很可能就有几个.”在学生的最近发展区设计有探究价值的题目，鼓励学生参与其中，实现做中学、学中悟，从而实现学生数学素养的提升.

总之，2017年的浙江省数学高考试卷，打破了高考中的文科生和理科生的固定思维模式，开启了文理合卷的新篇章，高考试题无论在考查学生的数学基础知识方面，还是在学生驾驭知识的应用能力上都达到了选拔人才的效果，在数学试卷中更多地强调了每位考生必须具备的数学核心素养的考核，更加有利于高中数学教学的可持续性.正所谓素养本天成，向量妙显之！

[1] 李学军,曲文瑞.平凡真功显 秒解素养现——由2017浙江省高中数学模拟卷17题说起[J].中学教研(数学),2017(4):39-41.

[2] 许钦彪.概念化教学是改进现代数学教学的有效途径[J].中学教研(数学),2017(6):1-6.

O123.1

A

1003-6407(2017)10-29-04