素变量混合幂丢番图不等式

张倩倩

(华北水利水电大学 数学与统计学院,河南 郑州 450046)

素变量混合幂丢番图不等式

张倩倩

(华北水利水电大学 数学与统计学院,河南 郑州 450046)

丢番图不等式;Hardy-Littlewood方法；Davenport-Heilbronn方法;素变量；混合幂

0 引言

现在，关于素变量丢番图不等式的逼近有了更多的结果，其中它的表达形式诸如λ1p1k1+λ2p2k2+…+λrprkr+η≤(maxpj)-σ，其中λ1,λ2,λ3,λ4是非零实数，η是任意给定的实数.ALESSANDRO GAMBINI[1]证明了r=4k1=1,k2=k3=2,k4=k的情况，得到结果15,σ=1-2/(11k)-16/(11k2(k+1))+ε.本文将证明以下定理.

定理1设η是任意给定的实数，假设λ1,λ2,λ3,λ4是非零实数, 不全同号, 并且λ1/λ2是无理数, 则不等式

λ1p1+λ2p22+λ3p32+λ4p43+η<(maxpj)-σ

(1)

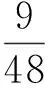
1 预备知识

在证明定理1之前, 首先做如下定义,其中η是任意给定的实数,ε与δ是足够小的给定的正数. 字母p不论是否带下标都表示素数. 因为λ1/λ2是无理数,用q表示λ1/λ2的渐近分数的分母. 设X=q2,通常写e(α)=e2πiα. 对任意j≥1, 有

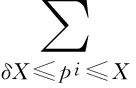
(2)

由素数定理及三角函数积分的一阶导数估计, 熟知有

(3)

傅里叶变换

(4)

则

Kτ(α)≪min(τ2,α-2)，

(5)

(6)

为了方便证明, 令

G(α)=S1(λ1α)S2(λ2α)S2(λ3α)S3(λ4α)Kτ(α)e(αη)，

H(α)=T1(λ1α)T2(λ2α)T2(λ3α)T3(λ4α)Kτ(α)e(αη),

并且对于实数集R的任意Lebesgue的可测子集Ω,记

(7)

根据(6)可以得到

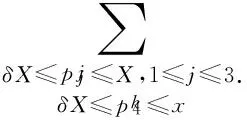
(8)

这里I(x)表示不等式

λ1p11+λ2p22+λ3p32+λ4p43+η<τ

(9)

现将实数集划分为两两不相交的3部分,M={αα≤P/X}，m={αP/X<αR},分别称为主区间、余区间与平凡区间.

2 主区间上的积分

先选取标准的主区间,因此可以得到I(τ,η,M)的一个下界. 显而易见下面的分解

(10)

接下来将逐一证明C1≫τ2X4/3及Ci=ο(τ2X4/3)，2≤i≤5.

2.1C1的下界

由以上可知

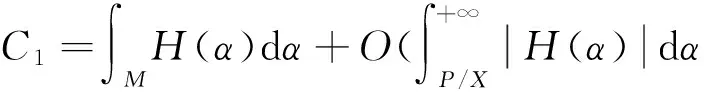
(11)

由(3), (6)和H(α)的定义, 能够得到(11)式右边的误差项符合

(12)

2.2C2的上界

首先，由欧拉求和公式可以得到

Uk(α)-Tk(α)≪1+αX.

(13)

有

(14)

为了估计A2, 引入Selberg积分, 对r≥1, 设

(15)

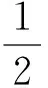
引理2[4]设r是大于或等于1的实数,ε是任意小的正常数, 则存在与r无关的正常数c1=c1(ε), 使得

对于X1-5/(6r)+1≤h≤X一致成立.

引理3[2]设j是大于或等于2的实数, 则对于任意实数A≥6, 有

根据柯西不等式, 引理3及(3)可得

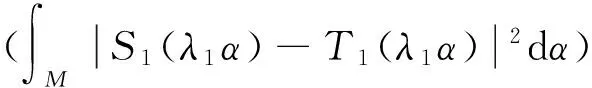
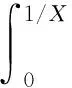
X4/3(logX)-A/2

(16)

由(3)和(13)得

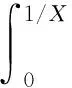
(17)

由(14), (16)和(17)得出C2≫τ2X4/3.

2.3C5的上界

由于C3,C4,C5是相似的, 因此只估计C5. 为了得到C5的一个比较好的上界，需要用到下面的引理.

下面开始估计C5, 由(5)可以得出

(18)

由引理4和推论1可得

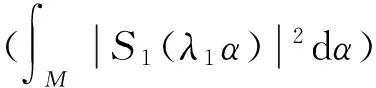
X(XlogX)1/2(X-1/3(logX)-A)1/2≪

X4/3(logX)(1-A)/2.

(19)

且由引理4及(13)得出

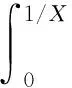
(20)

式(20)必须满足X+XP2=ο(τ2X4/3)，则有P

由(18),(19)及(20)得出C5=ο(τ2X4/3).由前面结论，取P=X1/6.

3 平凡区间上的积分

根据算数―几何平均不等式, 有

(21)

式(21)满足X4/3(logX)2/R=ο(τ2X4/3)，所以有R=τ-2(logX)2.

4 余区间上的积分

m1={α∈m:S2(λ1α)

下面只对m1做积分. 由引理4和Hölder不等式得

(22)

因为式(22)等于ο(τ2X4/3)，因此取τ=X-9/48.

下面讨论在m*上的积分,下面式子同时成立:

S1(λ1α)>X1-1/8+ε,S2(λ2α)>X1/2-1/16+ε,P/X=X-5/6<α≤τ-2log2X.

根据文献[1]中的方法, 将m*分成不相交的集合E(Z1,Z2,y), 对于α∈E(Z1,Z2,y)有

Z1

这里Z1=2k1X1-1/8+ε,Z2=2k2X1/2-1/16+ε,y=2k3X-5/6-ε,k1,k2,k3是非负整数.为了方便计算, 将E(Z1,Z2,y)记作Α, 利用文献[6]Lemma 6可以得到Α的勒贝格测度.

引理6[1]μ(Α)≪yX5/2+εZ1-2Z2-4.

证明见文献[1]Lemma 5.5.

由引理6可得

(23)

所以τ=X-9/48是最好的选择.

综上所述, 在余区间m上有

(24)

5 定理的证明

选τ=X-9/48，根据文中在主区间、余区间及平凡区间上得到的结论可推出I(τ,η,)≫τ2X4/3, 因此, 根据(10)能够得出I(x)≫τX4/3(logX)-4.

这就说明不等式(11)有≫τX4/3(logX)-4组素数解p1,p2,p3,p4, 其中Pj∈[δX,X](2≤j≤3),P1∈[δX,X],P34∈[δX,X].根据τ的选取和maxpj≈X,能够得出λ1p11+λ2p22+λ3p32+λ4p43+η<(maxpj)-σ式右端σ的范围. 由于λ1/λ2是无理数, 它的渐近分数的分母q有无限多个, 因此当q→∞时, 一定有X→∞, 即说明了解数的无限性, 得出了定理的证明.

[1] GAMBINI A. Diophantine approximation with one prime,two squares of primes and one k-th power of a prime[J/OL].[2017-06-30].https://arxiv.org/abs/1703.02381.

[2] MU QUAN WU, LV XIAO DONG. Diophantime approximation with prime variable and mixed powers(II)[J]. Advances in mathematics (China),2017，46(2):190-202.

[3] LANGUASCO A, ZACCAGNINI A . On a ternary Diophantine problem with mixed powers of primes[J]. Acta Arithmetica, 2013, 159(4):345-362.

[4] GAMBINI A, LANGUASCO A, ZACCAGNINI A. A Diophantine problem with two prime and one k-th power of a prime[J/OL].[2017-06-30].https://arxiv.org/abs/1706.00343.

[5] LANGUASCO A, ZACCAGNINI A. A Diophantine problem with a prime and three squares of primes[J]. Journal of Number Theory, 2012, 132(12):3016-3028.

[6] MU Q. Diophantine approximation with four squares and one k-th power of primes[J]. The Ramanujan Journal, 2016, 39(3):481-496.

MixedVariablesDiophantineInequalitywithPrimeVariables

ZHANG Qianqian

(CollegeofMathematicsandStatistics,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450046,China)

Diophantine inequality; Hardy-Littlewood method; Davenport-Heilbronn; prime variable; mixed power

2017-07-25

张倩倩(1994—)，女，河南驻马店人，华北水利水电大学数学与统计学院在读硕士研究生，研究方向：数论.

10.3969/j.issn.1007-0834.2017.03.004

O156.4

A

1007-0834(2017)03-0018-05