混合整数典范DC规划问题的分支定界算法

马艳利, 强 华, 冯娟婷

(银川能源学院 基础部，宁夏 银川 750021)

混合整数典范DC规划问题的分支定界算法

马艳利, 强 华, 冯娟婷

(银川能源学院 基础部，宁夏 银川 750021)

针对一类混合整数典范DC规划问题，提出了一个基于切平面的分支定界缩减方法.该方法用约束条件的切平面将可行域线性化，并使用了二分规则.数值结果表明所提出的算法是可行的,可以求解大规模问题.

混合整数；典范DC规划；分支定界；切平面

0 引言

混合整数非线性规划问题广泛存在于机械、化工、资源管理、生产调度、军事等领域.在混合整数非线性规划问题的研究中，确定型算法是将这个问题分解为相对容易求解的混合整数线性规划问题.随着科学技术的发展和实际中复杂决策问题求解的迫切需要，非线性整数规划问题的算法研究已经成为运筹学与最优化领域的研究热点之一.求解非线性整数规划问题的确定性方法有外逼近法[1-2]、分支定界法[3-7]、割平面法[8]、分解算法[9]等.由于整数规划问题是NP(non-determinstic polymial)问题,现有算法仅可求解某种特殊形式的整数规划问题，且往往存在计算量大、收敛速度慢、效率差等不足，甚至特殊的非线性整数规划问题——整数二次规划问题,至今还没有一个通用而有效的算法.

DC(differences of two convex functions)规划问题是一类重要的优化问题，任何一个DC规划都可以转换成典范DC规划问题，从而求解DC规划问题的最优解就转变成求解典范DC规划问题的最优解.在边际跟踪算法的基础上加入二分规则和取整要求，使得混合整数规划典范规划问题转化成整数典范DC规划问题，并用分支定界算法进行求解.许多工程问题中会遇到类似的求解问题，因而研究混合整数典范DC规划问题的全局解具有十分重要的现实意义.

本文结构：第1节描述了典范DC规划问题及可行域的整超矩形化；第2节主要是利用切平面将约束函数线性化的过程，这是本文的主要内容之一；第3节是基于切平面的分支定界算法，这是本文的主要内容.

1 典范DC规划问题

本文考虑带有一般约束的混合整数典范DC规划问题：

其中x=(x1,x2,…,xn),c∈Rn,gi(x):Rn→R,I=1,2,3…是凸的非线性函数,g(x)=θ(x)-γ(x)，θ(x)和γ(x)是Rn上的凸的非线性函数.D为非空有界集，决策向量x为非负整数向量.

下面介绍典范DC规划问题的最优性满足的必要条件.

定义1[10]定义在凸集X∈Rn上的实值函数f称为X上的DC，是指对于所有x∈X，f能够表示成f(x)=p(x)-q(x)，其中p(x)，q(x)是X上的凸函数.

定理1[10](最优性必要条件)对于典范DC规划，假设D是有界的，F非空，并且反向约束g(x)≥0是实质的，G={x∈Rn:g(x)≤0},∂G表示G的边界，那么它在D和G的边界的交集∂D∩∂G上存在最优解.此外，当D是多胞形时，在D的边界与G的边界的交集上.

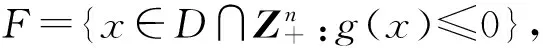
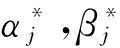
(1)

(2)

R相当于一个大箱子，把可行域F包起来，问题在R上的最优解就是F最优解.

2 典范DC规划约束函数的线性化

典范DC规划的约束函数是非线性的，利用非线性函数的切平面近似地代替非线性函数，使得可行域R线性化，便于可行域的分解.下面介绍具体的方法.

将约束函数g(x)=θ(x)-γ(x)在R-=[a-,b-]⊂R=[a,b]上线性化.函数θ(x)在点x0的切平面为

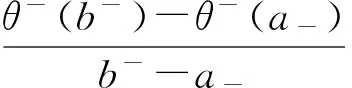
θ-(x)是θ(x)的切平面，θ(x)是凸的，有θ(x)≥θ-(x)，所以有如下不等式

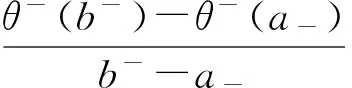
得到约束函数的线性下界.

令

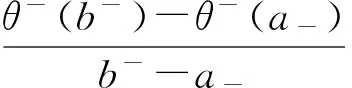
则得到典范DC规划问题的线性松弛问题DC*：

3 基于切平面的分支定界算法

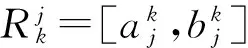
fori=1,2,…,m

do begin

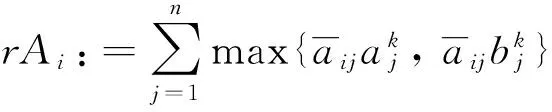
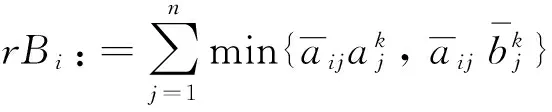
then停止．问题DC*在Rk上没有可行解(Rk被删除)；

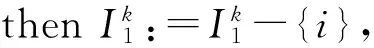
forj=1,2,…,n

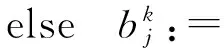
endif；

enddo

endif；

Enddo

该算法加入二分规则，将可行区域按整数点切分.

下面介绍整超矩形分支定界算法.

假设迭代到第k步，F表示问题DC*的可行域，W表示当前所找到的可行点的集合.

1)(初始化)构造包含F的n维超矩形R0=[a0,b0]⊆Rn，让W={a0,b0}∩F；解线性规划问题DC*，得到的最优值和最优解分别记为η,xη，其中xη所在的超矩形记为Rη，η是问题DC*全局最优值的一个下界．

如果xη∈F，让W=W∪{xη}，γ=min{f(x):x∈W}；

如果W=φ,那么γ=+∞；如果W≠φ，那么γ=min{f(x):x∈W}，并找一个当前的最优解xγ∈argminγ；

让T={R0}，k=1．

2) (终止规则)如果η-γ<ε，则停止计算，输出问题DC*的全局最优解xγ，全局最优值f(xγ)；否则转到下一步．

3)(选择规则)在T中选择超矩形Rk，其中Rk是η对应的超矩形，即η=η(Rk).

4) (剖分规则)

deleteRk=[lk,uk]，保留最优解xk；

else 运用上面超矩形的剖分方法，把超矩形Rk剖分为两个子超矩形Rk1，Rk2，且intRk1∩intRk2=φ;

endif;

5)(缩减技术)对剖分后的子超矩形进行以下缩减，为了方便起见，把缩减后产生的新的超矩形仍然记为Rki,i∈Γ，其中Γ是缩减后的超矩形的指标集.

ifak1=bk1

delete，保留最优解xk1；

else 运用上面超Rk1矩形的缩减技术，把Rk1进行缩减，

ifRk1被删除

T=T{Rk}，转到3)；

elseT=T{Rk}∪{Rk1}

解线性规划松弛问题(CDC1(Rk1))，得到最优值记为ηk1，最优解记为xk1；

解线性规划松弛问题(DC*(Rk2))，得到最优值记为ηk2，最优解记为xk2；

6)(定上界)

如果W=φ，那么γ=γ；

如果W≠φ，那么γ=min{f(x):x∈W}，当前最优解xγ∈argminγ．

7)(剪支规则)

让T=T{R:η(R)≥γ，R∈T}．

8) (定下界)

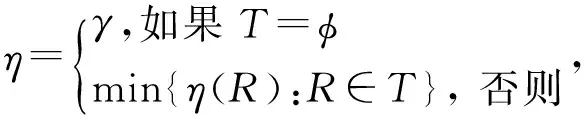
置k←k+1．转到2．

4 算例

考虑问题：

通过MATLAB数值试验，得到问题的最优解为x1=1,x2=0,x3=-1.

[1] FLETCHER R, LEYFFER S. Solving mixed intger nonlinear programs by outer approximation[J].Mathematical Programming, 1994(66):327-349.

[2] BERGAMINI M L, SCENNA N, AGUIRRE P. An improved piecewise outer-approximation algorithm for the global optimization of MINLP models involving concave and bilinear terms[J]. Computers and Chemical Engineering, 2008(32):477-493.

[3] MATHUR K, SALKIN H, MORITO S. A branch and search algorithm for a class of nonlinear knapsack problems[J]. Operations Research Letters,1983 (2):155-160.

[4] JUAN M , GROSSMANN E .A branch and contract algorithm for problems with concave univariate, bilinear and linear fractional terms[J]. Journal of Global Optimization ,1999,14:217-249.

[5] STUBBS R, MEHROTEA S. Abranch-and-cut method for 0-1 mixed convex programming[J]. Mathematical Programming, 1999,86:512-532.

[6] 陈志平，李乃成，郤峰．解复杂二次整数规划问题的新型分支定界算法[J]．工程数学学报，2004,3(21):371-376．

[7] IVO NOWAK, STEFAN VIGERSKE. LaGO: A (heuristic) branch and cut algorithm for nonconvex MINL-Ps[J].CEJOR, 2008(16): 127-138.

[8] WESTERLUND T, PETTERSSONV F. A cutting plane method for solving convex MINLP proplems [J].Comuter and Chemical Engineering, 1995,19(S):131-136.

[9] FLIPPO O, RINNOY K A. A note on benders decomposion in mixed-integer quadratic programming[J].Operations Research Letters,1990 (9):81-83.

[10] 黄红选，梁治安. 全局优化引论[M]. 北京：清华大学出版社，2003:31-32．

MixedIntegerModelforDCProgrammingProblemofBranchandBoundAlgorithm

MA Yanli, QIANG Hua, FENG Juanting

(DepartmentofBasic，CollegeofEnergyResourcesofYinchuan，Ningxia750021，China)

Based on a class of mixed integer model for DC programming problems, puts forward a new branch and bound method. In this method, the constraint function is used to be linear and we also use binary rules. Numerical results show that the proposed algorithm is feasible and large-scale problems can be solved.

mixed integer; model for DC planning; branch and bound; tangent plane

2017-05-25

银川能源学院科研项目资助(2015-KY-Y-29)

马艳利(1987—)，女，陕西榆林人，银川能源学院基础部教师.

10.3969/j.issn.1007-0834.2017.03.003

O24

A

1007-0834(2017)03-0013-05