逻辑回归模型中的混合最大似然估计
左卫兵, 李英莉
(华北水利水电大学 数学与统计学院, 河南 郑州 450046)
逻辑回归模型中的混合最大似然估计
左卫兵, 李英莉
(华北水利水电大学 数学与统计学院, 河南 郑州 450046)
针对逻辑回归模型中解释变量存在复共线性问题, 通过类比线性模型中的混合估计, 提出了逻辑回归模型中的混合最大似然估计; 在均方误差矩阵意义下, 将新估计与最大似然估计、岭估计、Liu估计、约束最大似然估计、随机约束最大似然估计比较, 最后通过蒙特卡罗模拟方法验证其优良性.
逻辑回归; 复共线性; 随机约束岭估计; 均方误差矩阵
0 引言
本文考虑如下模型
yi=πi+εi,i=1,2,…,n,
(1)
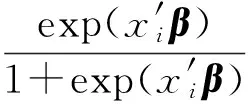
最大似然估计是估计参数β的常用方法,β的最大似然估计表达式为
(2)
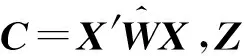
文献[1]提出了逻辑岭估计为
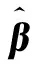
(3)
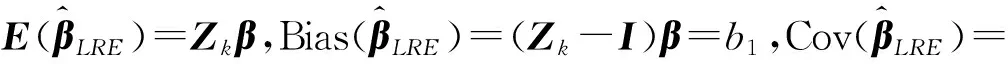
文献[2]提出了逻辑Liu估计为
(4)
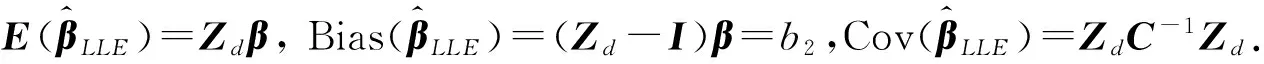
考虑如下约束条件
h=Hβ+v;E(v)=0, Cov(v)=Ψ,
(5)
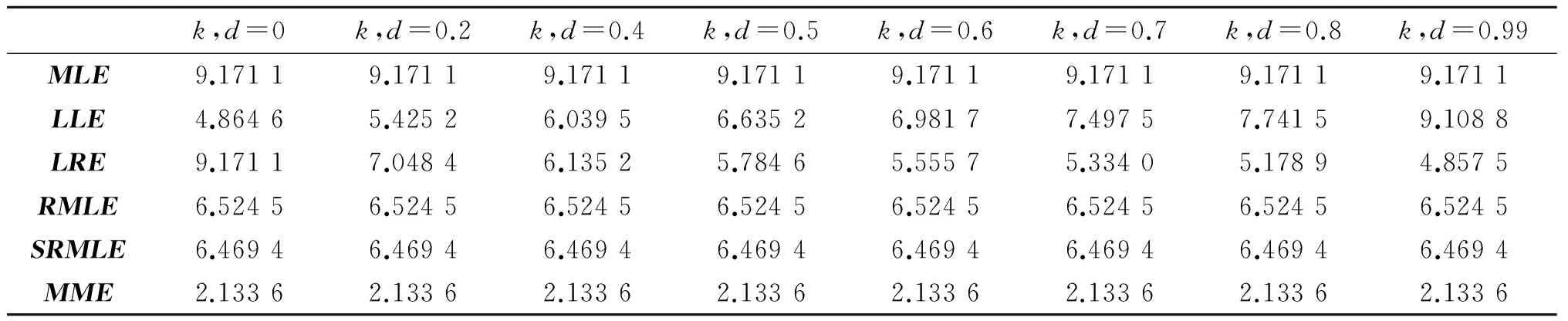
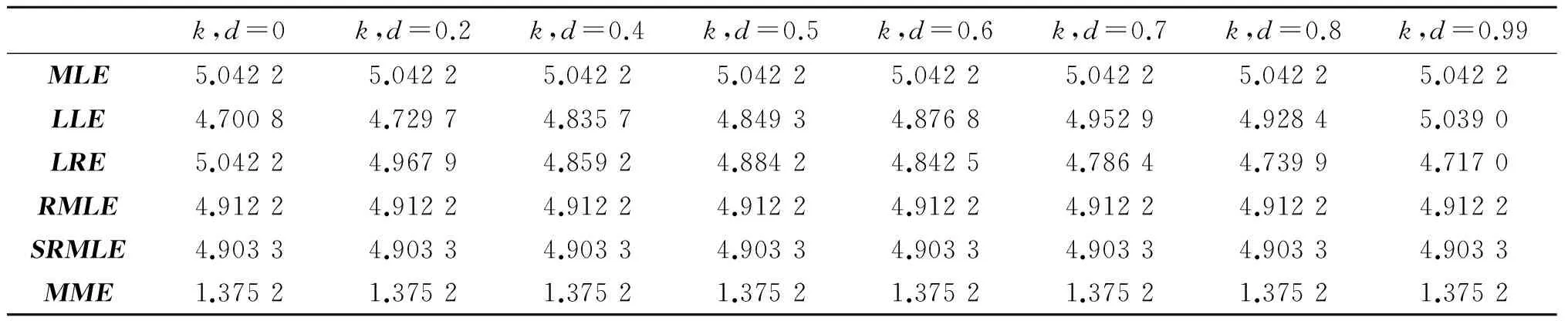
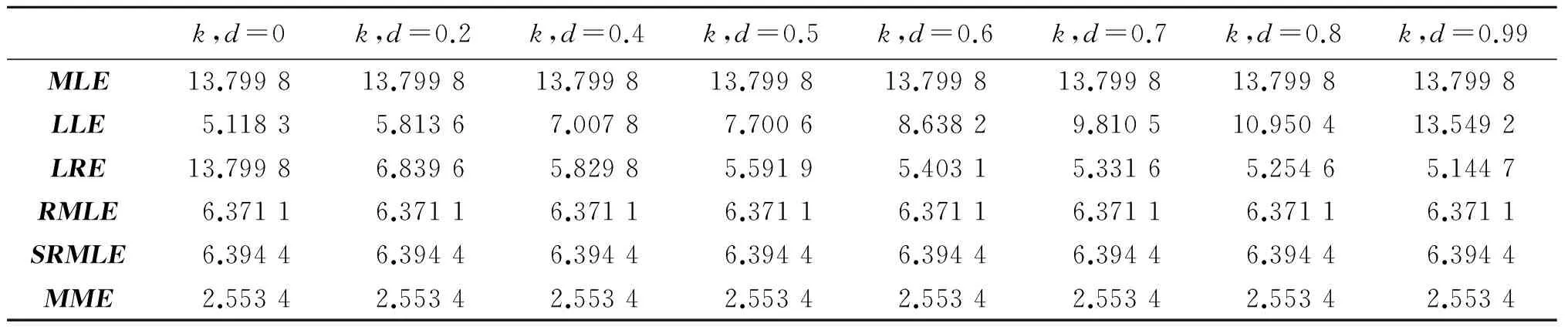
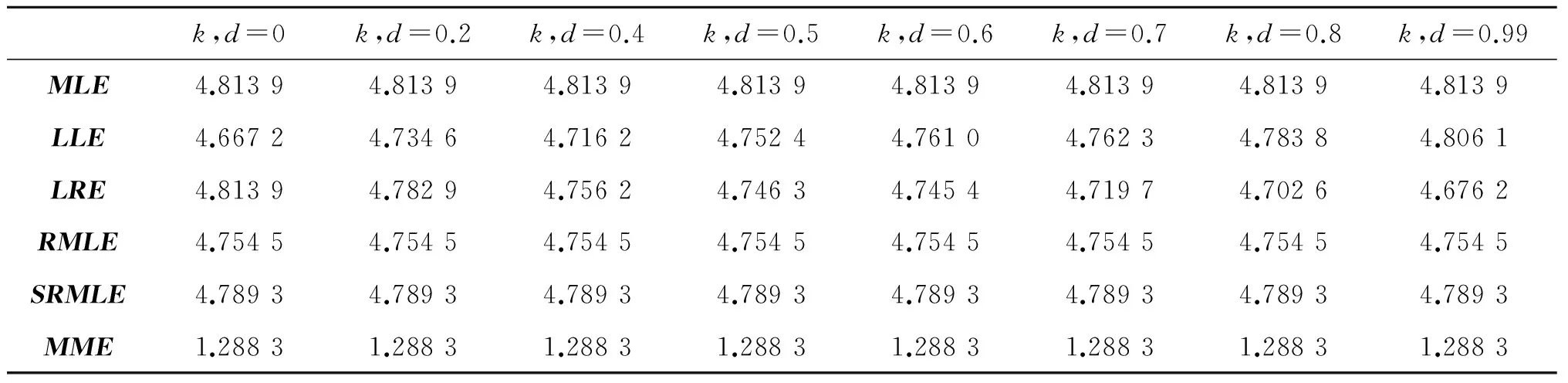
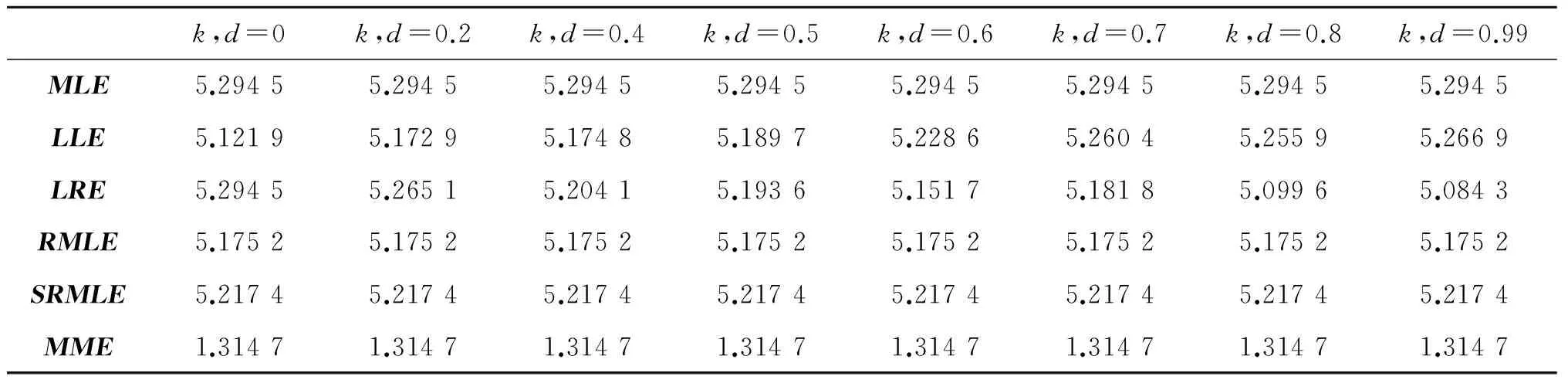
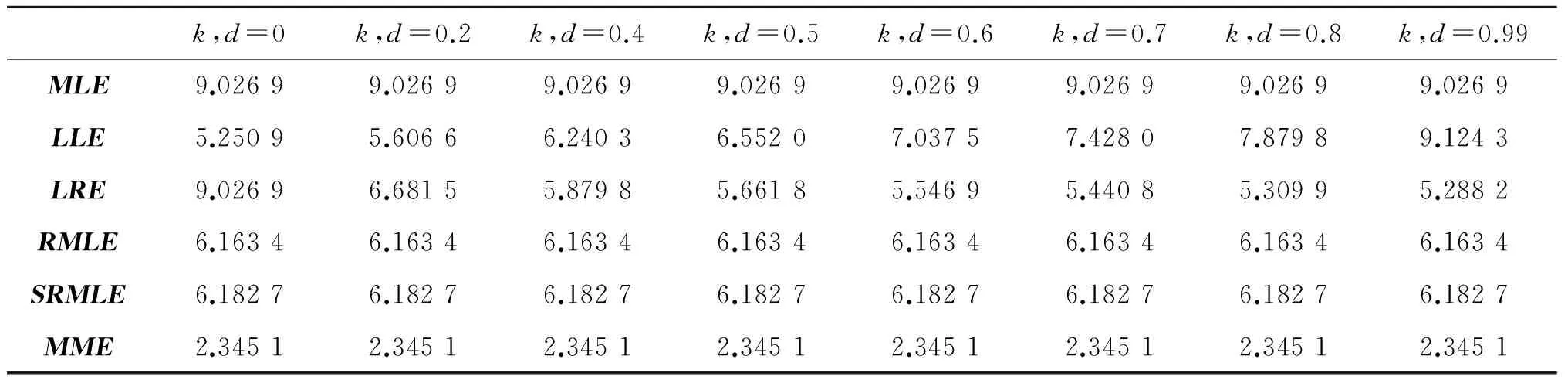
其中h为q×1阶随机已知变量,H为一个已知的q×(p+1)(q 在线性约束条件下, 文献[3]提出了约束最大似然估计为 (6) 在随机线性约束条件下, 文献[4]提出了随机约束最大似然估计为 (7) 本文通过类比文献[5] ,线性模型中的混合估计提出逻辑回归模型中的混合最大似然估计,定义如下 (8) 符号说明:A>0表示A为对称正定方阵,A≥0表示A为对称半正定方阵,A≥B表示A≥0,B≥0且A-B≥0. 引理1[6]A为n×n矩阵,B为n×n矩阵,若A>0,B≥0,则A+B>0. 引理2[7]M为n×n矩阵,N为n×n矩阵,若M>0,N≥0,则M>N当且仅当λmax(NM-1)<1. 证明 C-1-C-1+C-1H′(Ψ-1+HC-1H′)-1HC-1=C-1H′(Ψ-1+HC-1H′)-1HC-1, (9) 显然,C-1H′(Ψ-1+HC-1H′)-1HC-1>0,以上定理得证. 证明 (10) 证明 (11) 证明 (12) 证明 (13) 本文采用文献[8-10]的方法进行蒙特卡罗模拟. 生成解释变量使用下面的方程 xij=(1-ρ2)1/2zij+ρzi,p,i=1,2,…,n,j=1,2,…,p, (14) 此外,我们选择以下约束 (15) 对于参数d、k,选择0≤d<1、0≤k<1. 重复模拟2 000次. 用式(16)模拟MLE、LLE、LRE、RMLE、SRMLE和MME的均方误差,结果见表1~表9. ME()=Mean{tr[MSEM(,β)]}=(-β)′(-β). 表2 n=20, ρ=0.80,对于不同k与d,各个估计的均方误差Tab.2 The estimated MSE values for different k,d when n=20 and ρ=0.80 表4 n=100, ρ=0.70,对于不同k与d,各个估计的均方误差Tab.4 The estimated MSE values for different k,d when n=100 and ρ=0.70 表5 n=100, ρ=0.80,对于不同k与d,各个估计的均方误差Tab.5 The estimated MSE values for different k,d when n=100 and ρ=0.80 表6 n=100, ρ=0.99,对于不同k与d,各个估计的均方误差Tab.6 The estimated MSE values for different k,d when n=100 and ρ=0.99 表7 n=200, ρ=0.70,对于不同k与d,各个估计的均方误差Tab.7 The estimated MSE values for different k,d when n=200 and ρ=0.70 表8 n=200, ρ=0.80,对于不同k与d,各个估计的均方误差Tab.8 The estimated MSE values for different k,d when n=200 and ρ=0.80 表9 n=200, ρ=0.99,对于不同k与d,各个估计的均方误差Tab.9 The estimated MSE values for different k,d when n=200 and ρ=0.99 由表1~表9可知,当ρ变大时,上述6个估计的均方误差会变大; 当n增大时,上述6个估计的均方误差会减小. 但是,对于所有的n、ρ、k,新估计MME均优于MLE、LRE、LLE、RMLE、SRMLE. 本文针对逻辑回归模型中解释变量存在复共线性问题,提出一种混合最大似然估计. 在均方误差矩阵意义下,得到了优于最大似然估计、岭估计、Liu估计、约束最大似然估计、随机约束最大似然估计的充分或充要条件,并且用蒙特卡罗模拟方法验证了其优良性. 在保证均方误差不增大的前提下,如何降低新估计的偏差是下一步研究的重点. [1] SCHAEFER R L, ROI L D, WOLFE R A. A ridge logistic estimator[J].Communication in statistics: Theory and methods, 2007, 13:99-113. [2] DENIZ INAN, BIRSEN E E. Liu-type logistic estimator[J]. Communication in statistics: simulation and computation, 2013, 42:1578-1586. [3] DUFFY D E, SANTNER T J. On the small sample prosperities of norm-restricted maximum likelihood estimators for logistic regression models[J]. Communications in statistics: Theory and methods, 1989, 18(3): 959-980. [4] NAGARAJAH V, WIJEKOON P. Stochastic restricted maximum likelihood estimator in logistic regression model[J]. Open Journal of Statistics, 2015, 5(7):1-6. [5] THEIL H. On the use of incomplete prior information in regression analysis[J]. Journal of the American Statistical Association, 1963, 58(302):401-414. [6] RAO C R, TOUTENBURG H. Linear Models: Least Squares and Alternatives[M]. 2nd Ed. New York: Springer-Verlag Inc,1995. [7] RAO C R, TOUTENBURG H, SHALABH, HEUMANN C. Linear Model and Generali-zations[M]. Berlin: Springer, 2008. [8] TRENKLER G, TOUTENBURG H. Mean squared error matrix comparisons between biased estimators: An overview of recent results[J]. Statistical Papers, 1990, 31(1):165-179. [9] GOLAM KIBRIA B M. Performance of some new ridge regression estimators[J]. Communication in Statistics: Simulation and Computation, 2003, 32(2):419-435. [10] DONALD, GARY C, GALARNEAU, et al. A Monte Carlo evaluation of some ridge-type estimators[J]. Journal of the American Statistical Association, 1975, 70(350):407-416. MixedMaximumLikelihoodEstimatorinLogisticRegressionModel ZUO Weibing, LI Yingli (CollegeofMathematicsandStatistics,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450046,China) Proposes the mixed maximum likelihood estimation in the logistic regression model with stochastic linear restrictions which is through the mixed estimation in the linear model of the explanatory variables in the logistic regression model. In the mean square error matrix sense, the new estimation is compared with the maximum likelihood estimation, ridge estimator, Liu estimator, restricted maximum likelihood estimator and stochastic restricted maximum likelihood estimator. Finally, the Monte Carlo simulation method is used to verify the superiority of the new estimation. logistic regression; multicollinearity; stochastic restricted ridge estimator; mean squared error matrix 2017-04-11 河南省基础与前沿技术研究项目(142300410401) 左卫兵(1976—), 男, 河南内黄人, 华北水利水电大学数学与统计学院教授, 硕士生导师,主要研究方向:数理统计. 通信作者:李英莉(1991—), 女, 河南郑州人, 华北水利水电大学数学与统计学院硕士研究生, 主要研究方向:数理统计. 10.3969/j.issn.1007-0834.2017.03.001 O212.1 A 1007-0834(2017)03-0001-06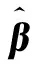
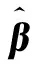
1 混合最大似然估计
2 估计的优良性
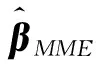


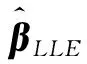
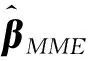
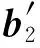
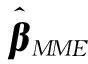
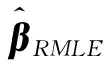
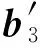
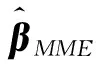
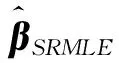
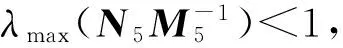
3 蒙特卡罗模拟
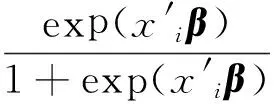
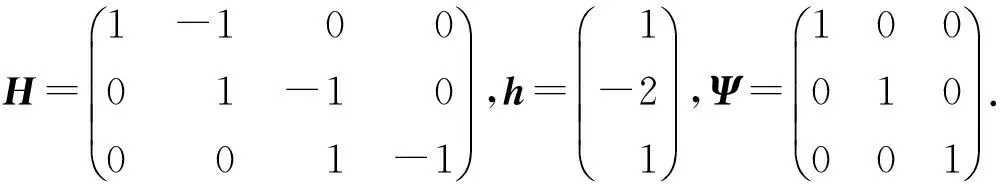


4 结论

