2017年高考全国I卷文理第22题试题分析与备考建议

广东省广州市第四中学(510170) 刘运科

2017年高考全国I卷文理第22题试题分析与备考建议

广东省广州市第四中学(510170) 刘运科

2017 年是广东使用全国I卷的第二年,今年有超过90%的考生在第22题、第23题之间选择了第22题.本文结合考生的答题情况,对第22题进行了分析,给出了备考建议,希望对“坐标系与参数方程”的高考备考教学有所启发.

一、原题及解法

1.原题 (2017年高考全国I卷文理第22题)在直角坐标系xOy中,曲线C的参数方程为

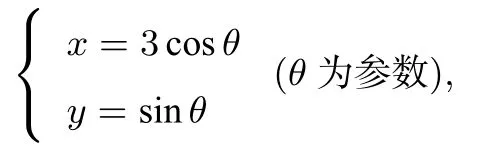
直线l的参数方程为

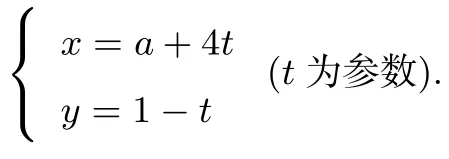
(1)若a=−1,求C与l的交点坐标;

(2)若C上的点到l的距离的最大值为求a.

2.分析 本题主要考察的知识点有:曲线的参数方程与普通方程的互化,直线与曲线的位置关系(相交、相离),解方程(组),点到直线(两平行线)的距离公式,三角函数的辅助角公式(合一变形),三角函数的值域等.本题涉及到的数学思想方法有:转化与化归思想、函数与方程思想、分类讨论思想、数形结合思想等.

3.解答

第一问解法一a=−1时,直线l的方程为x+4y−3=0.曲线C的标准方程是联立方程

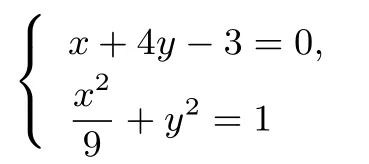
解得C与l交点坐标是(3,0)和

第一问解法二 由a=−1得到

其中t,θ为参数.故消去θ可得25t2−26t+1=0,解得t=1或.t=1时,得交点(3,0);时,得交点.故C与l交点坐标是(3,0)和

第一问解法三 由a=−1得到

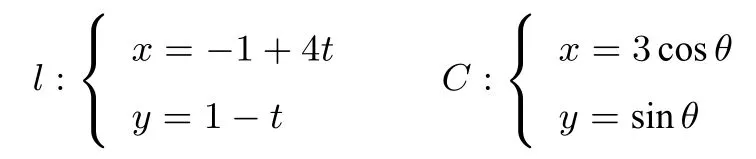
其中t,θ为参数.故

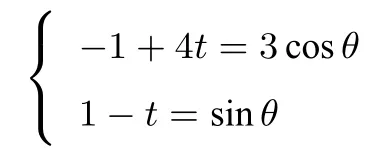
消去t可得4sinθ+3sinθ=3.由

注 只有极个别考生用解法二、解法三的方法求交点.第(1)问的思维上不存在难点,考生主要因为计算能力薄弱而失分.

第二问解法一 直线l一般式方程为:x+4y−4−a=0.设曲线C上任意一点坐标为P(3cosθ,sinθ),则P到l距离

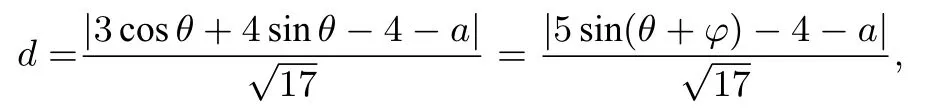
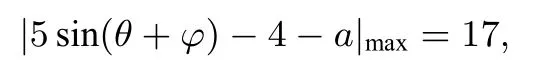
由−1≤sin(θ+φ)≤1,可得

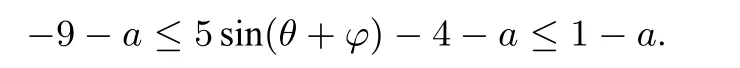
故|5sin(θ+φ)−4−a|max=max{|−9−a|,|1−a|},

令|−9−a|=|1−a|,得a=−4.

①当a≤−4时,|−9−a|≤|1−a|,从而有

0≤|5sin(θ+φ)−4−a|≤|1−a|,

由|1−a|=17,得a=−16或a=18(舍去);2

②当a＞−4时,|−9−a|＞|1−a|,从而有

0≤|5sin(θ+φ)−4−a|≤|−9−a|,

由|−9−a|=17,得a=8或a=−26(舍去).

综上,a=−16或a=8.

令判别式 ∆=64b2−4×25×(b2−9)=0,

得b=±5,故椭圆与直线l平行的切线为x+4y±5=0.①当a＞−4时,直线l∶x+4y−4−a=0与l2∶x+4y+5=0的距离解得a=8或a=−26(舍去);

②当a≤−4时,直线l∶x+4y−4−a=0与l2∶x+4y−5=0的距离解得a=−16 或a=18(舍去).

综上,a=−16或a=8.

注 多数考生采用解法一,少数考生用解法二.第(2)问最大的难点在于分类讨论,或者是求得了四个a的值,不知道如何取舍.

二、考生典型错误分析

第一问考生的典型错误如下

1.基本概念不清

(1)混淆参数方程与极坐标:由

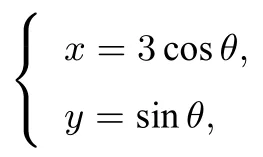
推得

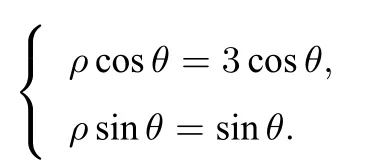
2.计算能力薄弱

第二问考生的典型错误如下

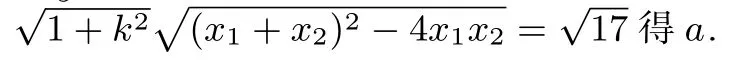
(2)审题失误,且基本方法错误:误以为是直线截椭圆的弦长等于将直线的非标准参数方程代入椭圆方程再得韦达定理,将其代入弦长公式得a.

(3)基本公式记忆错误:点P(x0,y0)到直线l的距离公式出现各种错误,如等.

(4)基本方法错误:对3cosθ+4sinθ进行合一变形时,出现各种错误,如 3cosθ+4sinθ=25sin(θ+37°)、

(5)不会用函数方法、分类讨论来解方程:

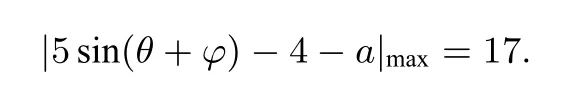
一些考生直接由|1−a|=17或|−9−a|=17,得a=−16或a=18或a=8或a=−26,不知道如何取舍.

(6)用解法二时计算错误:联立计算错误、判别式计算错误、切线错误.

(7)用解法二时求得了四个a的值,不知道如何取舍,或讲不清为什么舍去另外两个.

(8)解题不够严谨:如合一变形时,未指出辅助角φ的含义;最后一步不能正确地分类讨论,求得了四个a的值,不知道如何取舍,或讲不清为什么舍去另外两个.

(9)答题条理混乱,不够规范,缺乏必要的解题步骤.

三、备考建议

针对考生出现的上述错误,对“坐标系与参数方程”的高考备考教学,有如下建议:

1.要重视基本概念、基本方法的教学

(1)重视基本概念的教学,区分易混淆的概念.

在教学中要抓住关键,引导学生理解基本概念.例如,参数方程教学中,要让学生理解几个关键问题:什么叫参数方程?参数方程与普通方程的区别是什么?如何互化?几种常见曲线的参数方程中,参数的几何意义是什么?参数方程有哪些简单的应用?

(2)重视基本方法的教学.

对于常见的知识点,要总结方法,对比方法.例如,求圆的弦长,常见方法有:勾股定理、结合直线的标准参数方程的弦长公式(|AB|=|t1−t2|)、极坐标系中过极点的弦长公式(|AB|=|ρ1−ρ2|)、一般的弦长公式等.重视解题关键步骤,关注细节,形成解题技能.例如,求圆(椭圆)上的点到直线的最短距离问题,要让学生搞懂解题关键步骤:画图—设点的参数方程—代入距离公式—三角函数合一变形—三角函数的值域.

2.要加强计算能力的培养

(1)重视审题指导.

个别考生审题太快,看错题目,或思维固化,受记忆中的题目的干扰,错误地理解题意,导致审题失误,整体解题方向错误.在平时的教学中,要重视审题指导,提醒学生认真读题,认真分析题目,不要先入为主,准确理解题意,选择正确的解题方向.

(2)重视公式和定理的推导过程.

为什么有考生忘记或用错“点到直线的距离公式”?有的考生是考试紧张所致,更多的考生是因为没有理解公式,既不知道公式的由来,也不知道公式中字母的含义.在平时的教学中,要重视公式和定理的推导过程,分析公式定理的意义,帮助学生准确记忆、正确使用公式和定理.

(3)重视推理的严谨性,规范答题,做好解题示范.

考生一些计算错误,简单地看,是粗心大意,实际上是解题习惯不好.在平时的教学中,要重视推理的严谨性,规范答题,做好解题示范,不省略,不跳步,帮助学生养成良好的解题习惯.

(4)重视解题反思,重视方法的总结与对比.

3.要注意渗透数学思想方法

本题第二问较难,得分率低.主要有两种解法:函数法、平移相切法,思路如下:椭圆上的点到直线距离最远⇒点的参数方程代入距离公式,得到θ的函数⇒函数的最大值为椭圆上的点到直线的距离最远⇒直线平移与椭圆相切平行线间的距离为

多数考生用解法一.解法一的难点在于解方程:|5sin(θ+φ)−4−a|max=17.解此方程,本质上是用函数方法:令f(θ)=5sin(θ+φ)−4−a,由三角函数的有界性,易知f(θ)∈[−9−a,1−a];从而fmax(θ)=max{|−9−a|,|1−a|};令|−9−a|=|1−a|得a=−4,从而再按a≤−4,a＞−4进行分类讨论,难点得以突破.

如果用平移相切法,数形结合,有一种更简洁的解法:先求得两条切线x+4y±5=0,画图,再求出在椭圆上方且与直线l1∶x+4y+5=0距离为的直线方程x+4y−12=0,同理可求在椭圆下方且与直线l2∶x+4y−5=0距离为的直线方程x+4y+12=0,从而直线x+4y−4−a=0就是直线x+4y−12=0、x+4y+12=0,得a=−16或a=8.用这种方法,避免了分类讨论,思路直观,过程简洁优美.

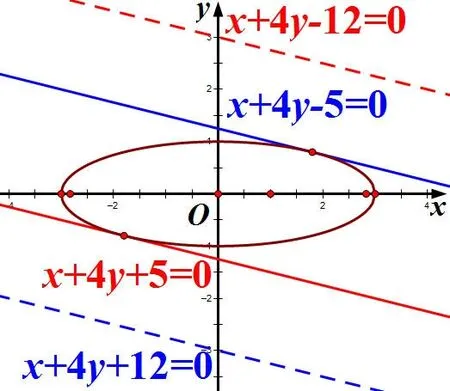
图1

波利亚说过,完善的思想方法犹如北极星,许多人通过它而找到正确的道路.数学思想方法是解题的指导思想和基本策略,在平时的教学中,要注意渗透数学思想方法,这对于学生在数学学习过程中,理解问题的数学本质,激发学习兴趣,促进思维发展,提高认知能力,发展创造能力,大有裨益.

[1]王印凡.2016年高考文、理科数学第23题广东考生答卷分析与思考[J].中学数学研究,2016(10).

[2]简洪权.高中数学运算能力的组成及培养策略[J].中学数学教学参考,2000(12).