（1+1）维经典Boussinesq-Burgers系统的留数对称和多孤子解

曹伟平，费金喜，李冀英

（1.丽水学院工学院，浙江丽水323000；2.丽水学院附属高级中学，浙江丽水323000）

（1+1）维经典Boussinesq-Burgers系统的留数对称和多孤子解

曹伟平1，费金喜1，李冀英2

（1.丽水学院工学院，浙江丽水323000；2.丽水学院附属高级中学，浙江丽水323000）

通过Painlevé截断展开得到（1+1）维经典Boussinesq-Burgers系统的留数对称，引入新的变量，延拓系统把留数对称局域到李点对称，获得该系统的有限变换。利用延拓系统，获得n次Bcklund变换和多孤子解。

Boussinesq-Burgers系统；留数对称；Bcklund变换；多孤子解

0 引言

随着非线性科学的不断发展，许多物理现象，如流体力学、等离子波、非线性光学、固体物理学、软凝聚态物质等[1-4]，都可以用非线性演化方程来描述。为了更好地理解这些物理现象的机制，寻找非线性演化方程的精确解和解的性质就显得十分重要。最近，楼森岳等[5-6]开展了一个极有吸引力的工作，即所谓的留数对称，提出了相关Painlevé截断展开的对称就是相对于奇性流形的留数。对非局域留数对称，可以通过引入适当的延长系统，使之局域到Lie点对称[7-11]，并找到相关的有限变换。

本文通过留数对称方法，得到（1+1）维经典Boussinesq-Burgers（CBB）系统的多孤子解。具体内容安排如下：首先讨论（1+1）维经典CBB系统的留数对称和相应的有限变换。其次利用留数对称的线性叠加和n次Bcklund变换获得多孤子解，并作一定的讨论。

1 非局域对称和局域化

考虑（1+1）维经典 Boussinesq-Burgers（CBB）系统[12-15]：

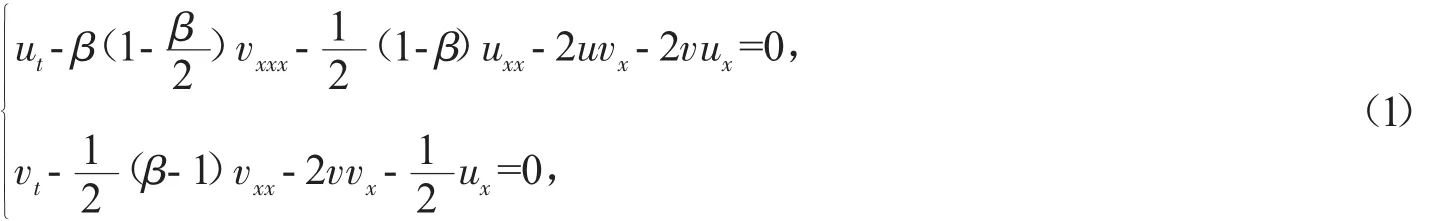
式中 u=u（x，t）是偏离水面平衡位置的距离，v=v（x，t）为水平速度矢量场，β 是色散常数。若 β=0，则式（1）可化简为经典Boussinsq系统。湖泊和海洋中的浅水波的形成和传播常用系统（1）来描述，因此研究它的精确解对港口和海岸设计有十分重要的帮助。

对CBB系统，根据齐次平衡定理，其Painlevé截断展开式为

式中 u0，u1，u2，v0，v1，f都是（x，t）的待定函数。将（2）式代入（1）式，得到

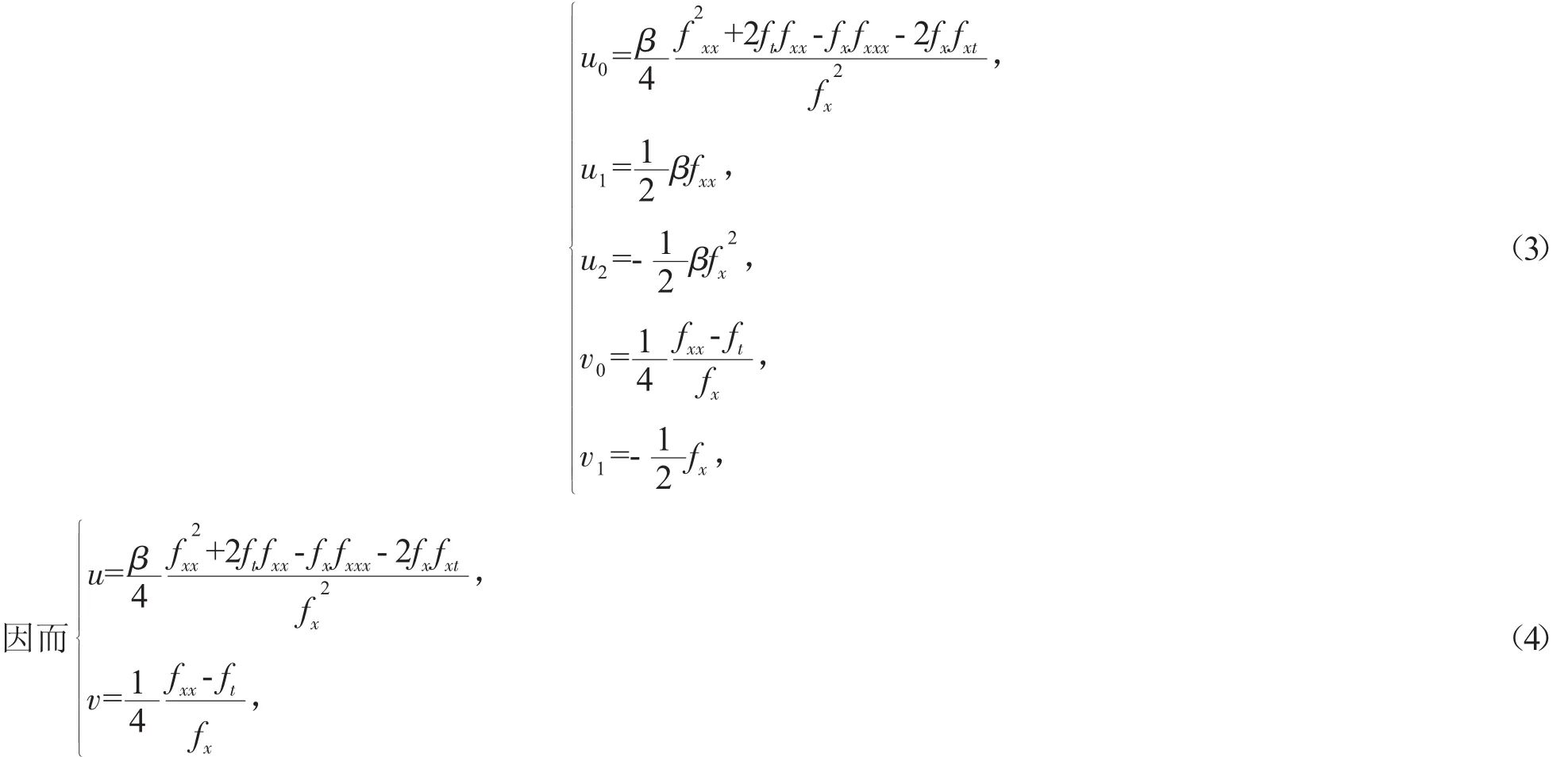
是CBB系统的一个解，且奇性流形f满足Schwarzian形式

（5）式中

Schwarzian（5）式在形式上保持不变。在特殊情形下，如取a=d=1，b=0，c=ε，ε为任意的群参量，则（5）式f的对称为

把f的对称（8）代入（4）式的线性化方程，得到CCB系统的非局域对称

从李对称定理可知，留数对称（9）连接着两个解。为了找出这两个解之间的关系式，则须解其初值问题，即

但是，对非局域对称（9），我们不能直接解初值问题（10）。为了求解初值问题（10），必须把CBB系统（1）进行延拓，使得在延拓系统中，能把非局域对称（9）局域到李点对称。为了使（9）式局域到李点对称，引入两个新的变量，即

因而由（1）、（5）和（11）组成的延拓系统，其李点对称为

相应的李点对称矢量场为

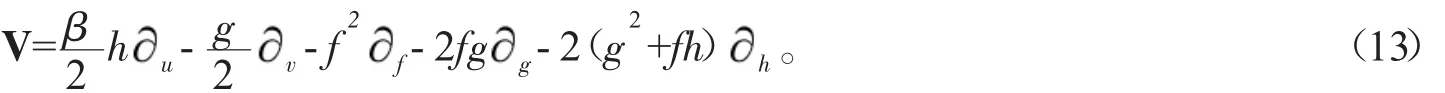
根据李点对称第一定理，解下列初值问题

得到系统（1）的李点对称群的有限变换

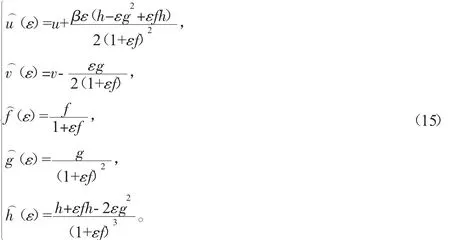
由于系统（1）的Schwarzian形式（5）具有无数个解，因而有无数个留数对称，即

对任意正整数n，（16）式中fi（i=1，2，…，n）是（5）式不同的解。因此有：

定理 1 如果 ｛u，v，fi，gi，hi｝是延拓系统

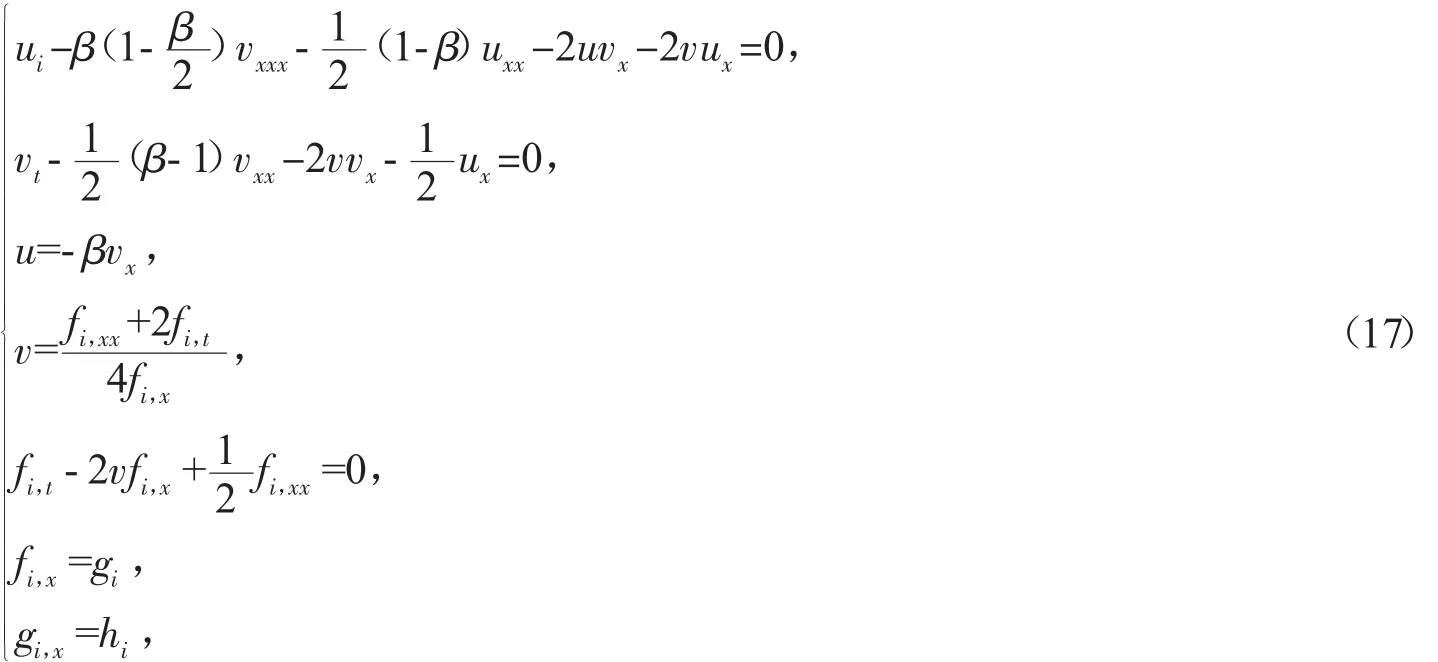
的一个解，则对称（16）可局域到李点对称

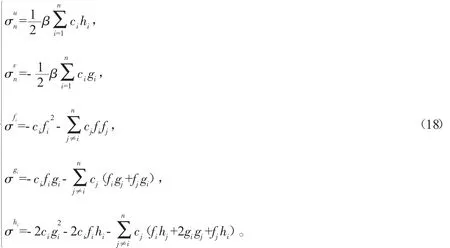
证明 延拓系统（17）的线性化方程为：

首先考虑特殊情形，即（16）式中取 i=k，cj=0（j≠k），由（12）式得到：

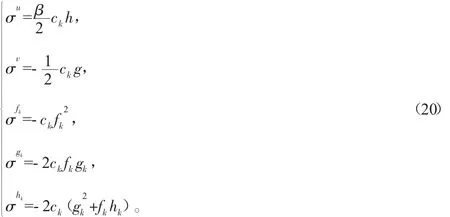
对（j≠k）情形，从（17）式中第 4式，分别令 i=k和 i=j，并消除 v可以得到

将 i=j和（21）式代入（19）式中第 4式有

显然（22）式解为

然后，对（23）分别求对x一阶和二阶导数可得

综合（20）（23）（24）定理 2 得证。

通过解（18）式的初值问题，即

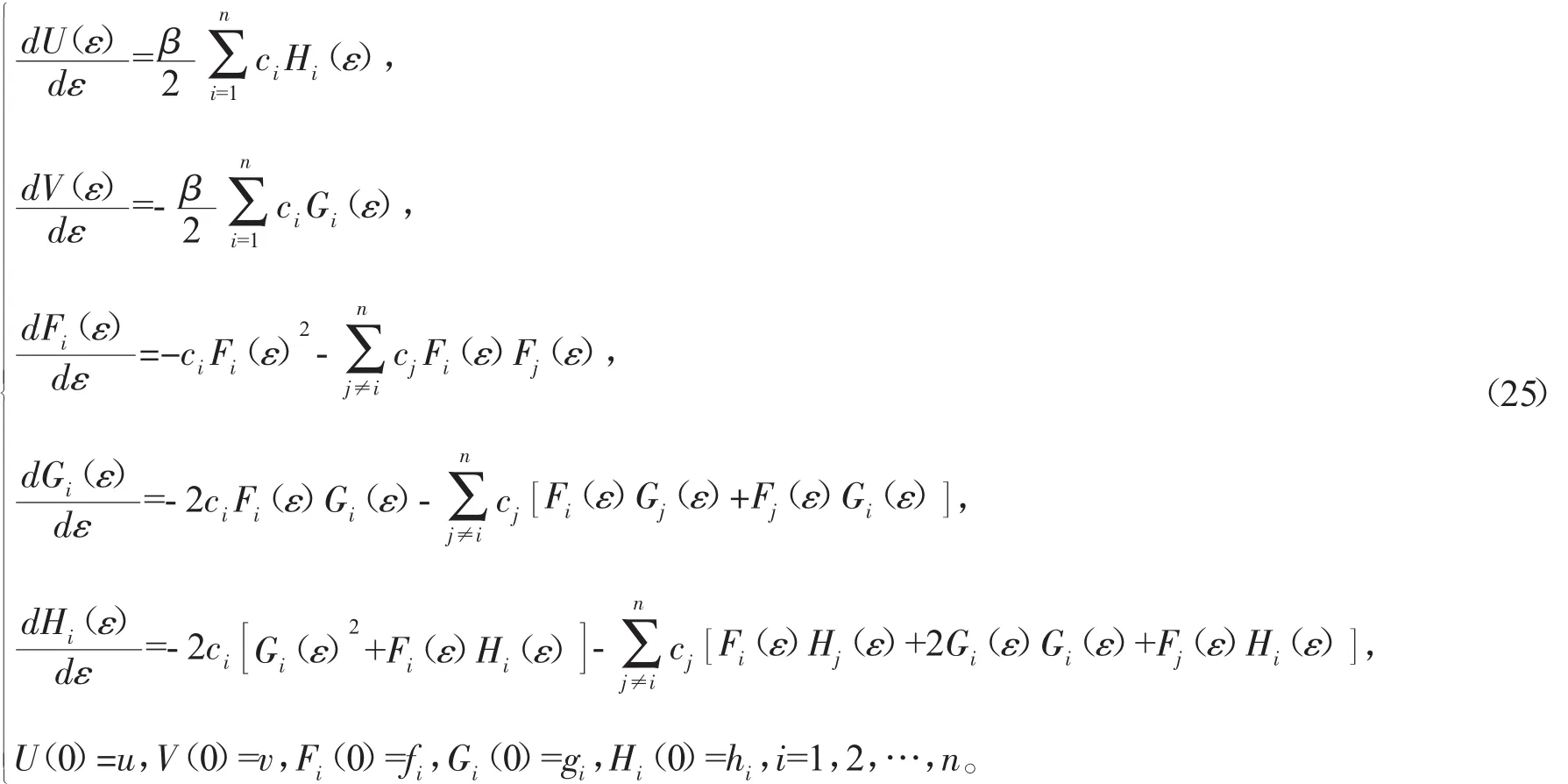
定理 2 如果 ｛u，v，fi，gi，hi｝是延拓系统（17）的解，则系统（1）有限变换为

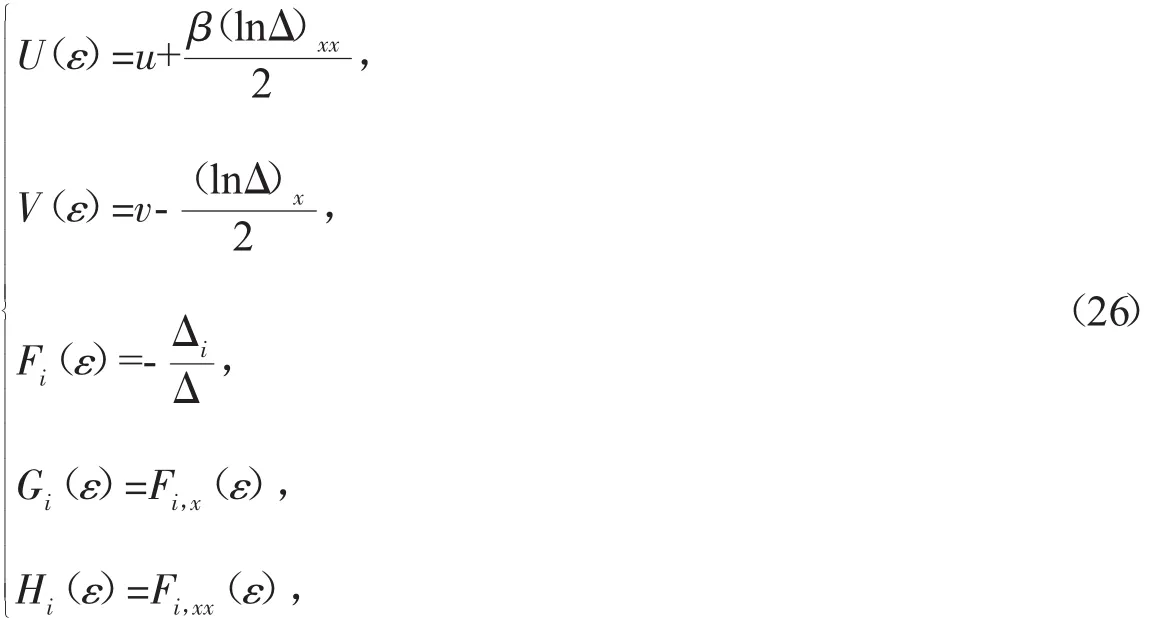
（26）式中

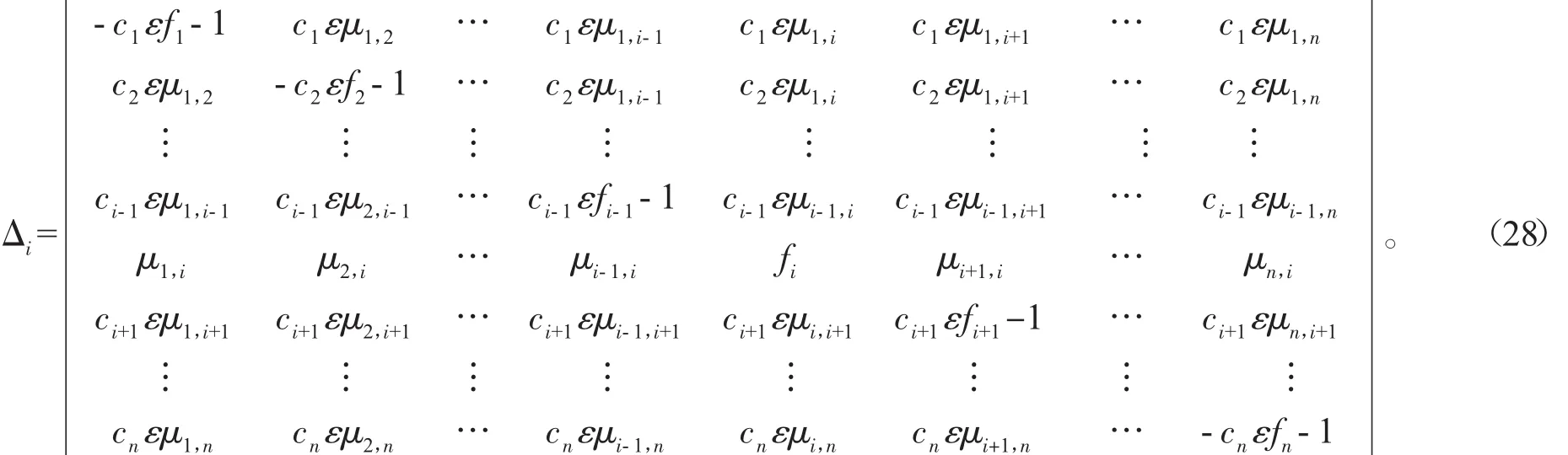
从定理2可以获得系统（1）的无数的精确解。显然，

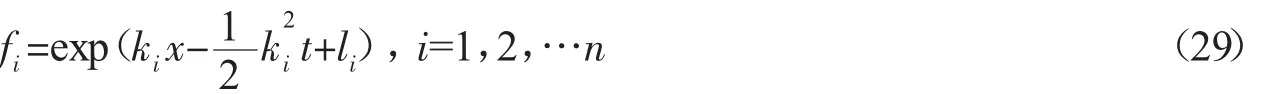
为（5）式的解，其中 ki，li为任意常数。例：若取 i=3，则由（27）可知

因此系统（1）的3孤子解为

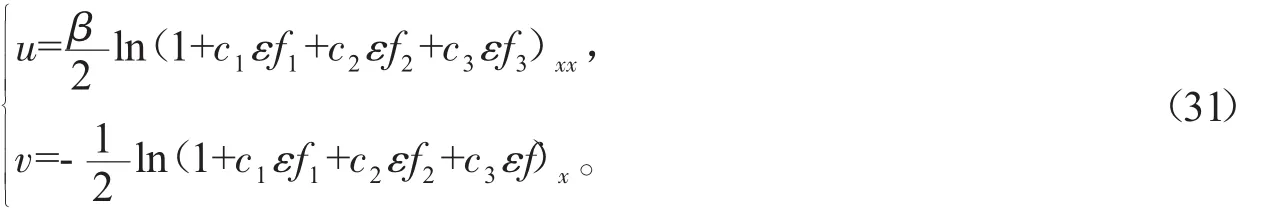
图1为（31）式表示的孤子裂变图，其中参数取为:

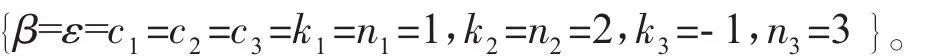
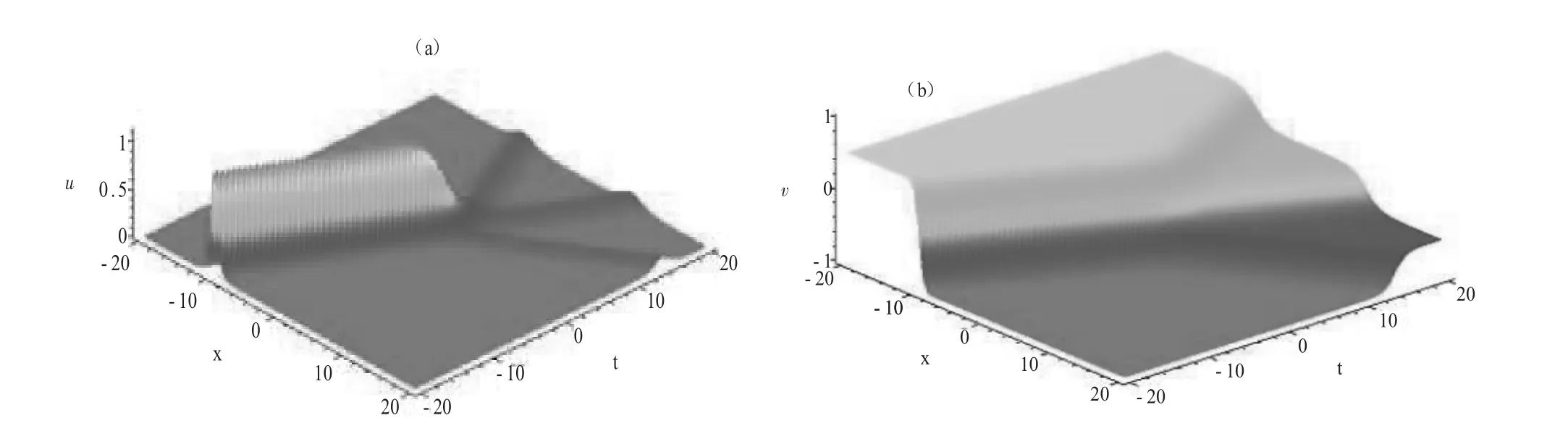
图1 （a）式（31）中u表达式的孤子裂变；（b）式（31）中v表达式扭结子裂变。

3 结语

通过引入合适的新的变量，与Painlevé截断展开相关的留数对称，可以局域到李点对称，获得（1+1）维经典Boussinesq-Burgers系统的n次Bcklund变换和多孤子解。留数对称的局域化过程，是求解非线性演化系统相互作用解的重要方法之一。

4 致谢

作者对陈勇、朱海平、方建平等专家的指导表示感谢。

［1］MESEGUER A，MELLIBOVSKYF.On asolenoidalFourier-Chebyshevspectralmethod forstabilityanalysis ofthe Hagen-Poiseuille flow［J］.Appl NumMath，2007，57（8）：920.

［2］TYAGI M，SUJITH R I.The propagation of finite amplitude gas dynamic disturbance in a stratified atmosphere around a celestial body:An analytical study［J］.Physica D，2005，211（1）：139.

［3］DERVOUT D T，VASSILEVSKI Y.Choice of initial guess in iterative solution of series of systems arising in fluid flowsimulations［J］.Comput Phys，2006，219（1）：210.

［4］TSOY E，AKHMEDIEV N.Dynamics and interaction ofpulses in the modified Manakovmode［lJ］.Opt Commun，2006，266（2）：660.

［5］LOU S Y，HU X R，CHEN Y.Nonlocal symmetries related to Bcklund transformation and their applications［J］.Phys A:Math Theor，2012，45（15）：155209.

［6］LOUSY.Residual symmetries and Bcklund transformations［J］.arXiv，2013，1308:1140v1.

［7］JIN Y，JIA M，LOU S Y.Nonlocalization of Nonlocal Symmetry and Symmetry Reductions of the Burgers Equation［J］.Commun Theor Phys，2012，58（6）：795.

［8］LIU X Z，YU J，REN B.Residual Symmetry Reductions and Interaction Solutions of（2+1）-Dimensional Burgers Equation［J］.Chin Phys B，2013，24（1）：8.

［9］LIU X Z，YU J，Ren B.New symmetry reductions related with the residual symmetry of Boussinesq equation［J］.arXiv，2013，1310：8512.

［10］LIUXZ，YUJ，RENB.Newinteraction solutions ofKadomtsev-Petviashvili equation［J］.Chin Phys B，2013，23（10）：1.

［11］LOUSY，LIANZJ.Searchingfor InfinitelyManySymmetries and Exact Solutions via Repeated SimilarityReductions ［J］.Chin Phys Lett，2005，22（1）：1.

［12］GENGXG，WUYT.Finite-band solutions ofthe classical Boussinesq-Burgers equations［J］.Math Phys，1999，40（6）：2971.

［13］ZHANG Y F，FENG B L.A few Lie algebras and their applications for generating integrable hierarchies of evolution types［J］.Commun Nonlinear Sci Numer Simul，2011，16（8）：3045.

［14］XUR.Darbouxtransformation and soliton solutions for classical Boussinesq-Burgers equation［J］.Commun Theor Phys，2008，50（3）：579.

［15］MEI J Q，MA Z Y.N-fold Darboux transformation and multi-soliton solutions for the classical Bousssinesq-Burgers system［J］.Appl Math Comput，2013，219（11）：6163.

Residual Symmetries and Multiple Soliton Solutions to（1+1）Dimensional Classical Boussinesq-Burgers System CAOWeiping1，FEI Jinxi1，LI Jiying2

（1.FacultyofEngineering，Lishui University，Lishui 323000，Zhejiang；2.The Affiliated Senior High School ofLishui University，Lishui 323000，Zhejiang）

The non-local residual symmetries related to truncated Painlevé expansion of Boussinesq-Burgers system are obtained.In order to localize the residual symmetries，we introduce new variables to prolong the original Boussinesq-Burgers to a new system.We obtain the finite transformation for the localized residual symmetry.Via prolonged system n-th Bcklund transformation and multiple soliton solutions are derived.

Boussinesq-Burgers system；Residual symmetry；Bcklund transformation；multiple soliton solution

10.3969/j.issn.2095-3801.2017.05.002

O411.1

A

2095-3801（2017）05-0008-08

2017-03-21；

2017-04-20

浙江省自然科学基金资助项目“带电粒子对受限高分子链输运性质的影响”（LQ14A040001）

曹伟平，男，浙江湖州人，副教授，博士。