非线性光纤方向耦合器中的行波解及动力学行为

吴晓飞，华国盛

（1.丽水学院工学院，浙江丽水323000；2.丽水学院信息技术中心，浙江丽水323000）

非线性光纤方向耦合器中的行波解及动力学行为

吴晓飞1，华国盛2

（1.丽水学院工学院，浙江丽水323000；2.丽水学院信息技术中心，浙江丽水323000）

借助于著名的齐次平衡原理和F-展开法的基本思想，研究非线性光纤方向耦合器系统中的非线性薛定谔方程组，得到满足传输方程的多种Jacobi椭圆函数周期波解和亮孤子解，并通过图形分析法，讨论其中一些解的动力学行为。

非线性薛定谔方程组；F-展开法；亮孤子解

0 引言

自从1980年Mollenauer、Stolen和Gordon[1]在实验室首次验证了光纤中可传输孤立子以来，光孤子在光纤中的传输理论与实验一直是人们的研究热点之一。由于光孤子在单模光纤中传输时可以保持形状不变，这为超高码速光纤通信提供了可能性。近年来，美、日、英等许多国家都致力于进行光孤子通信传输的实验，大力研发这一技术。例如，美国AT&T公司与日本KDD公司合作建设的越洋海底光缆，即TPC-6工程，就采用了光孤子传输技术，其传输能力达到了100 Gbit/s，距离在10 000 km以上。目前，光孤子传输实验的研究已获得了突破性的进展，其传输的码率和传输的距离分别可达到160 Gbit/s和106km以上，这为其实用化又更进了一步。然而，一个实用的全光孤子通信系统除了作为传输线的单模光纤以外，还包括脉冲变换器件，如光开关、光方向耦合器等。因此，研究光孤子在这些器件中的演化过程及其动力学行力，具有重要的理论意义和实际的应用价值。

非线性双芯光纤方向耦合器中的脉冲传输，在忽略交错相位调制的情况下，通常满足如下非线性薛定谔方程组

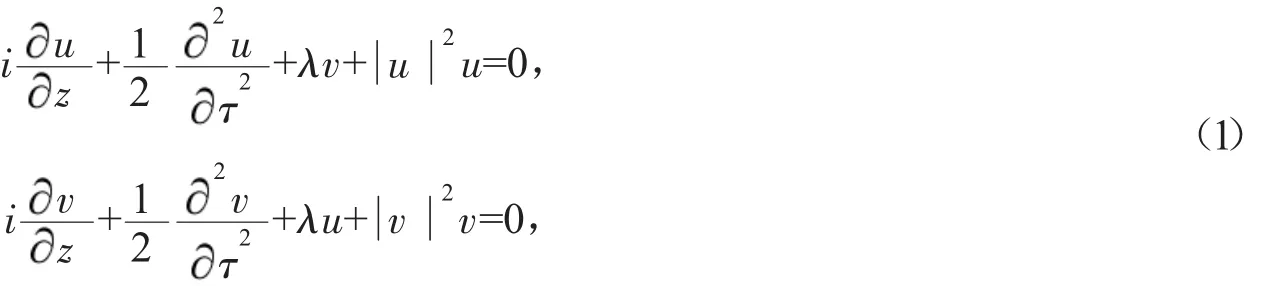
式中u，v分别为归一化后的1芯层和2芯层孤子振幅，z，τ，λ分别为归一化的距离、时间和耦合系数。若λ＝0，则方程组（1）就变为两个独立的非线性薛定谔方程，可以用反散射法精确地求出其N-孤子解。但由于交叉耦合的存在，方程组（1）是不可积的。本文拟利用著名的齐次平衡原理[2]和F-展开法[3]的基本思想来研究非线性光纤方向耦合器系统中的非线性薛定谔方程组，得到了满足传输方程的多种Jacobi椭圆函数周期波解和亮孤子解。

1 非线性薛定谔方程组的求解

首先对方程组（1）作行波约化，设

式中 ξ=z+cgτ，η=kz+ωτ，cg为群速，k 为波数，ω 为角频率。

将式（2）代入方程组（1）得φ，ψ满足的非线性常微分方程组

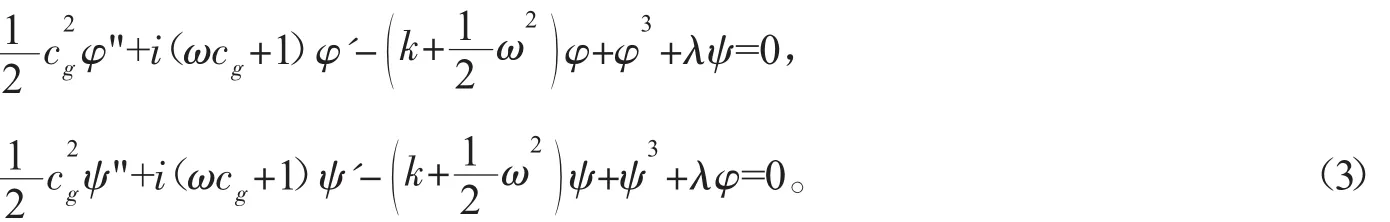
通常我们要求φ，ψ是实函数形式，故要求φ'，ψ'前的复系数为零，取ωcg+1=0，则方程组（3）简化为

依据F-展开法的基本思想，设方程组（4）的解的形式为

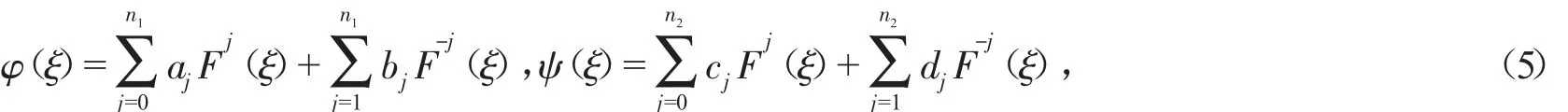
式中 n1，n2为正整数，a0，a1，…，an1，b1，…，bn1，c0，c1，…，cn2，d1，…，dn2为待定常数。F（ξ）满足常微分方程

式中P，Q，R为待定常数。

通过平衡方程组（4）中的最高阶导数项与非线性项，可确定n1=n2=1，于是由式（5）得到

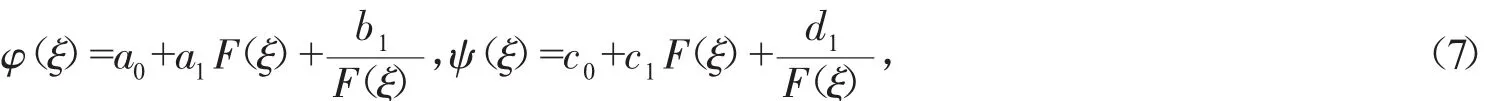
式中，a0，a1，b1，c0，c1，d1为待定常数。

将式（7）代入方程组（4），并利用式（6），合并F的同次幂项的系数，令F的各次幂项的系数为零，得到关于 a0，a1，b1，c0，c1，d1，cg，k，ω，P，Q，R 的代数方程组。然后，利用 maple软件解此代数方程组，可得满足方程组的解为：

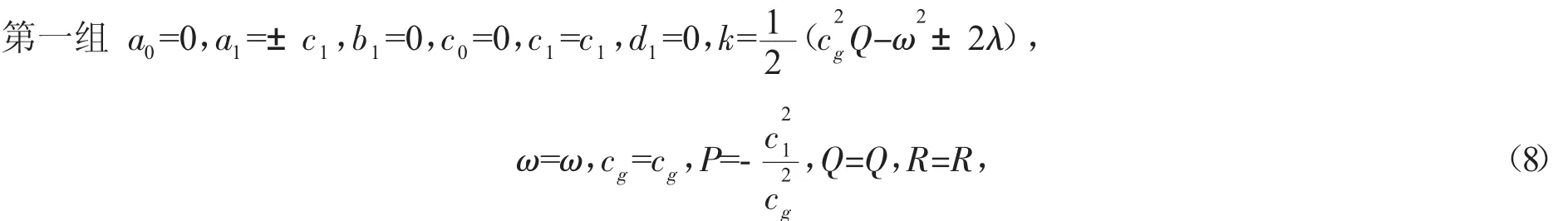
其中 c1，ω，cg，Q，R 为任意实数，且 ωcg+1=0；

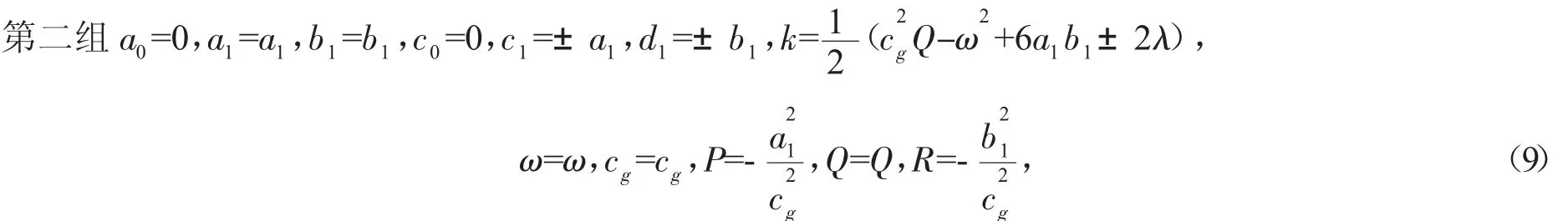
其中 a1，b1，ω，cg，Q 为任意实数，且 ωcg+1=0。

2 非线性薛定谔方程组的解的讨论

根据方程（6）、式（7）～ 式（9）和式（2），选取不同的 P、Q、R 值，可分别确定方程组（1）的不同的 Jacobi椭圆函数周期波解及孤子解。

2.1 Jacobi椭圆函数周期波解

（1）取P=-m2，Q=2m2-1，R=1-m2（m为Jacobi椭圆函数的模）时，F=cn（ξ），则方程组（1）的解为

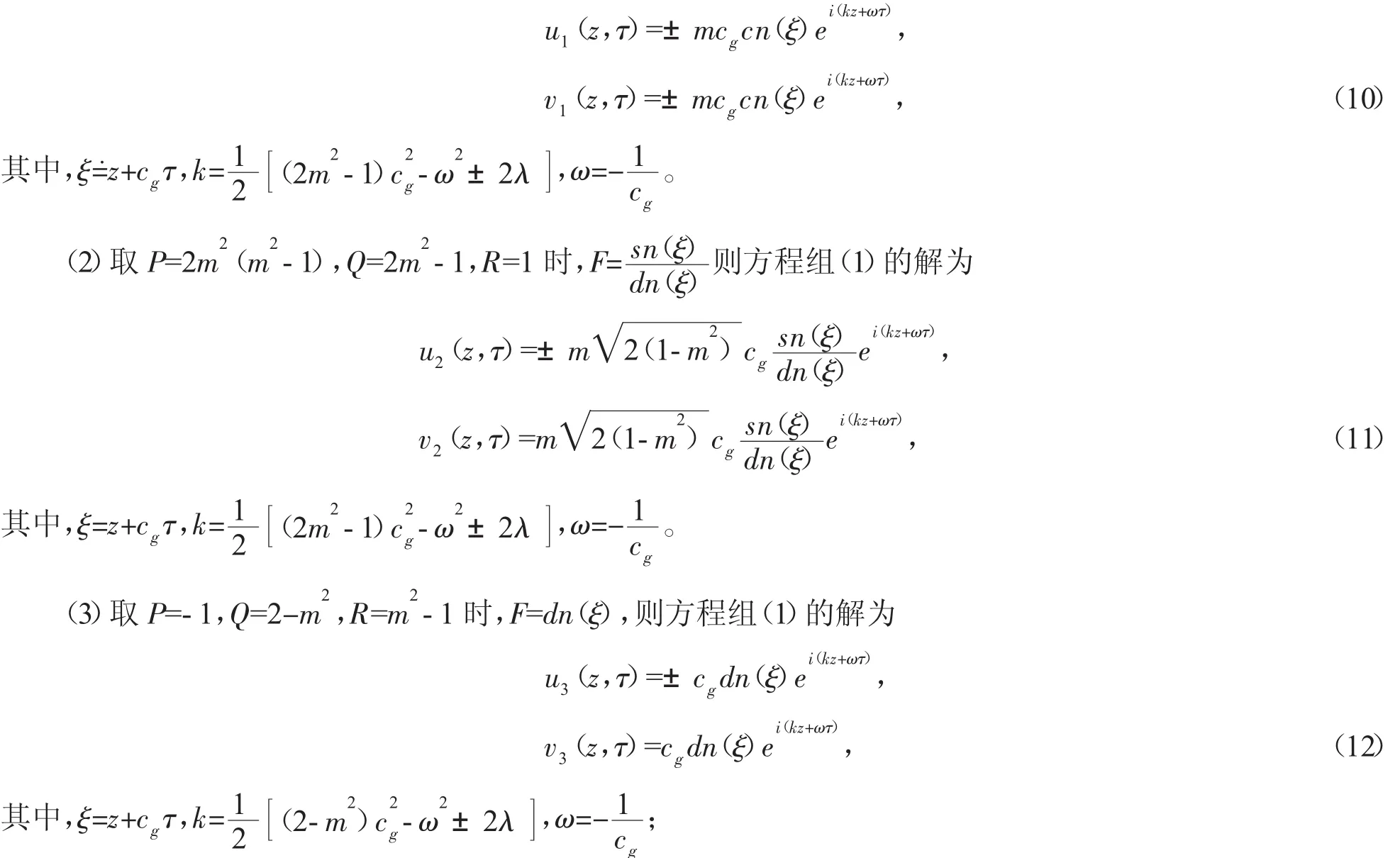
2.2 孤子解

当m→1时，由式（10）表示的Jacobi椭圆函数周期波解就退化为如下亮孤子解

2.3 图形分析

为了更直观地了解Jacobi椭圆函数周期波以及孤波的特性，利用计算机Maple软件对典型解进行模拟作图分析。

与解 u1的模所对应的周期波结构如图（1）所示，（a）取 cg=1，m=0.8时随 t变化的波形图，（b）取 cg=1，m=0.8，t=0时的波形截面图。与解u5的模所对应的m型周期波结构如图（2）所示，（a）取cg=1，m=0.1时随t变化的波形图，（b）取cg=1，m=0.1，t=0时的波形截面图。与解u6的模对应的类w型周期波结构如图（3）所示，（a）取cg=1，m=0.2时随t变化的波形图，（b）取cg=1，m=0.2，t=0时的波形截面图。与解 u7的模所对应的w 型周期波结构如图（4）所示，（a）取 cg=1，m=0.1 时随 t变化的波形图，（b）取 cg=1，m=0.1，t=0 时的波形截面图。与解u8的模对应的w-m组合型周期波结构如图（5）所示，（a）取cg=1，m=0.75时随t变化的波形图，（b）取cg=1，m=0.75，t=0时的波形截面图。与解u9的模所对应的孤波结构及孤波随时间的演化图如图（6）所示，（a）取 cg=1 时随 t的变化波形图，（b）取 cg=1，t=-5（实线），t=5（虚线）时的波形截面图，它是左行波，由实线曲线移动到虚线曲线。

因为u=±v，所以u的模的图形与v的模的图形是一致的。

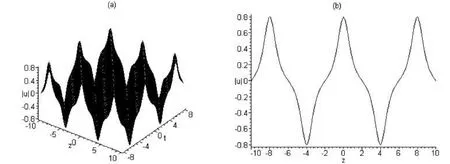
图1 与解u1的模对应的周期波结构图（（a）取cg=1，m=0.8时随t变化的波形图；（b）取cg=1，m=0.8，t=0时的波形截面图）

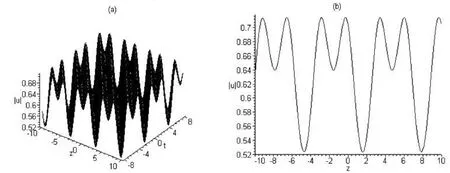
图2 与解u5的模对应的m型周期波结构图（（a）取cg=1,m=0.1时随t变化的波形图；（b）取cg=1，m=0.1，t=0时的波形截面图）

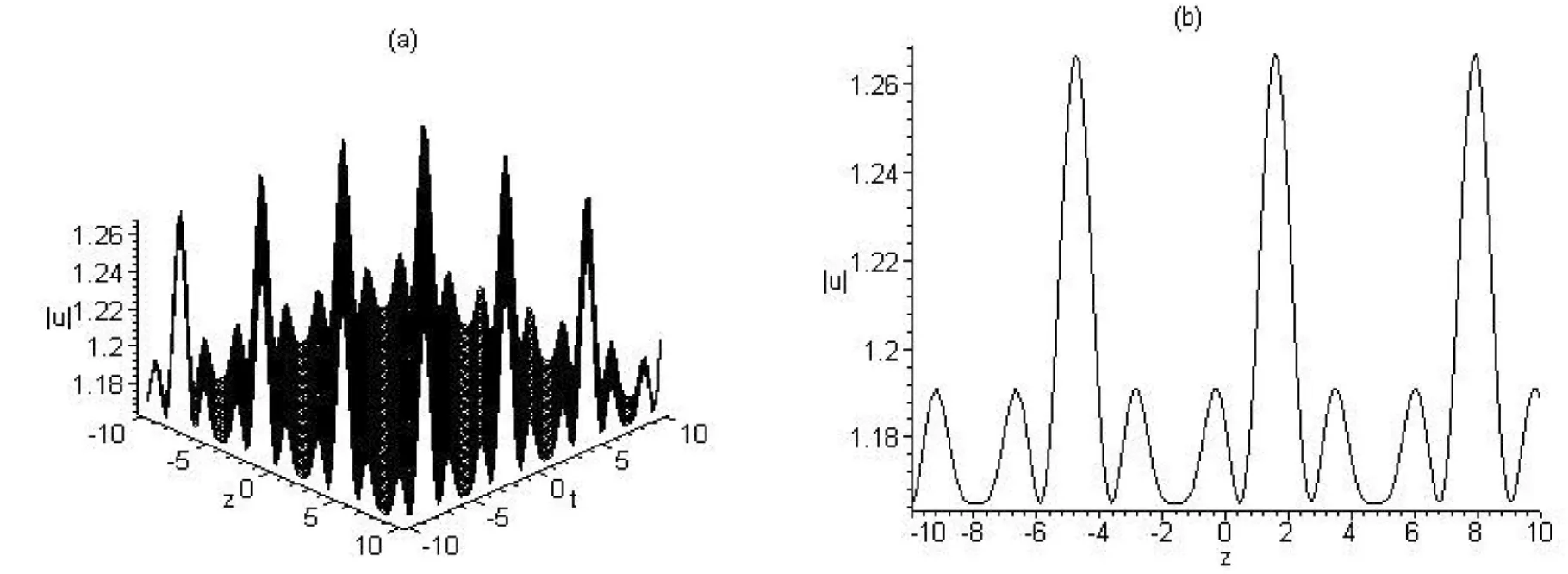
图3 与解u6的模对应的类w型周期波结构图（（a）取cg=1,m=0.2时随t变化的波形图；（b）取cg=1，m=0.2，t=0时的波形截面图）

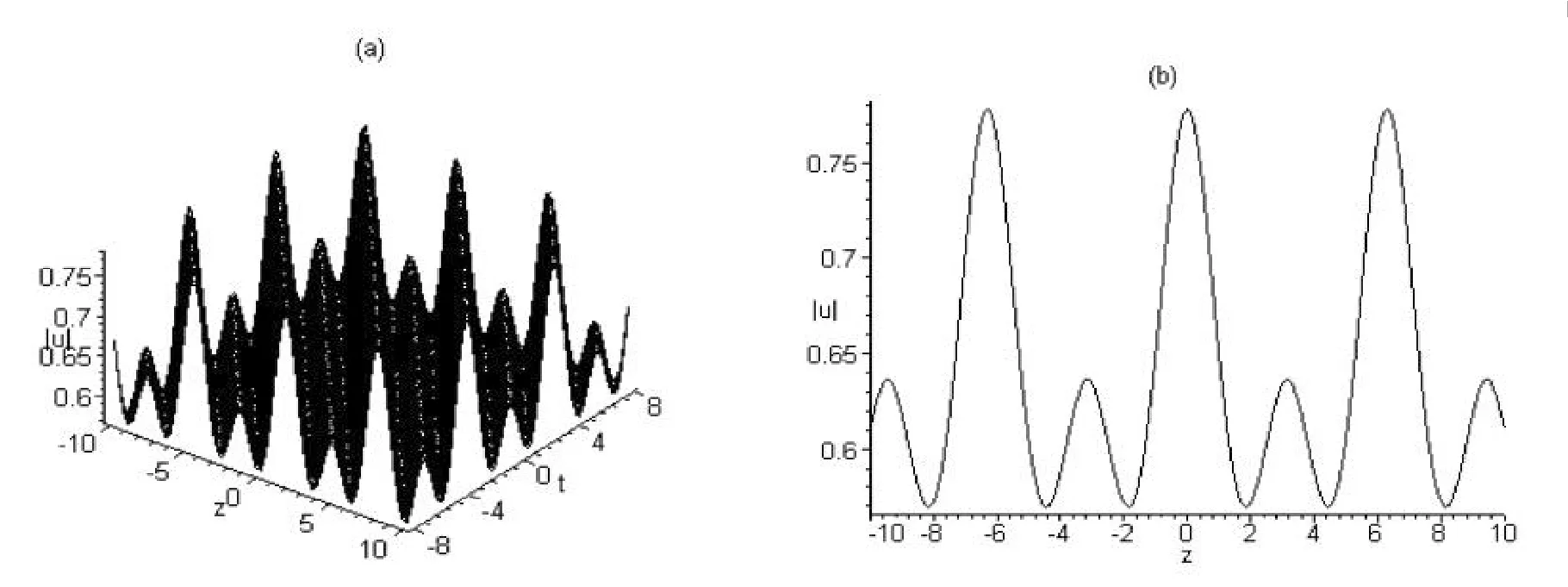
图4 与解u7的模对应的w型周期波结构图（（a）取cg=1,m=0.1时随t变化的波形图；（b）取cg=1，m=0.1，t=0时的波形截面图）

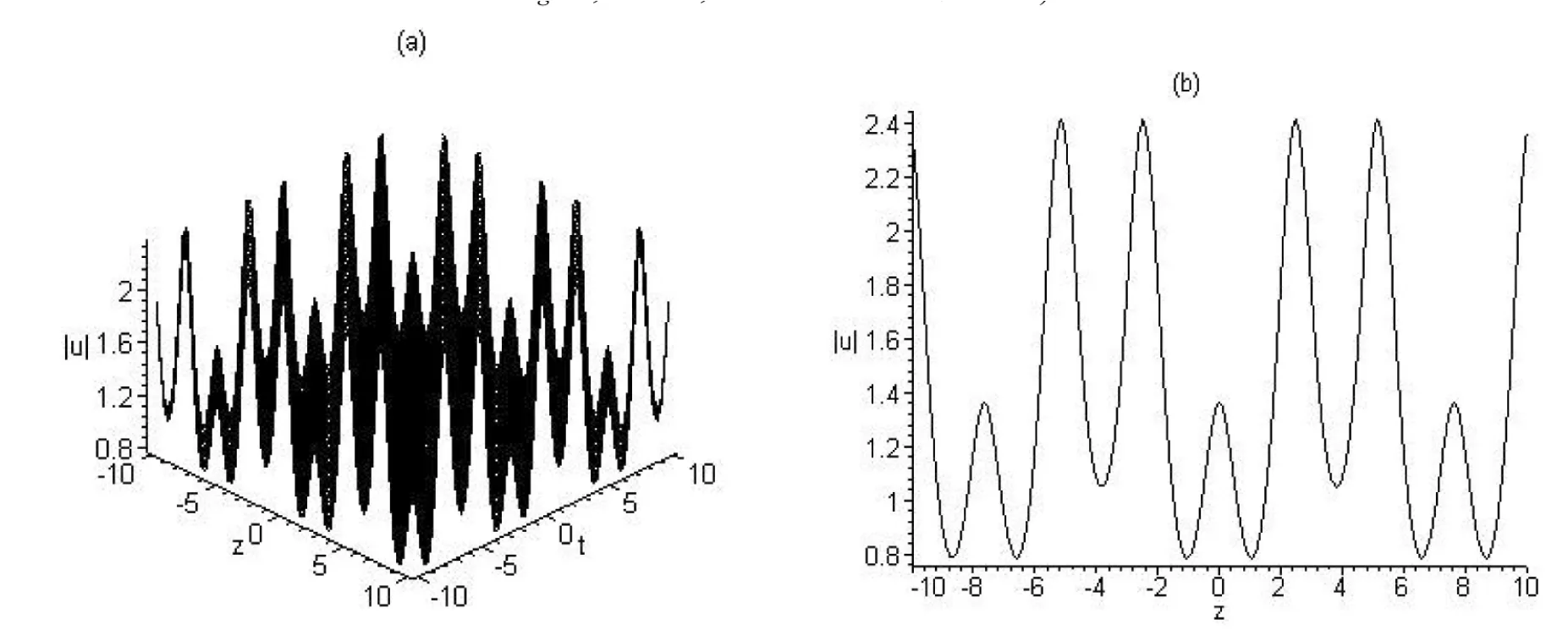
图5 与解u8的模对应的w-m组合型周期波结构图（（a）取cg=1，m=0.75时随t变化的波形图；（b）取cg=1，m=0.75，t=0时的波形截面图）

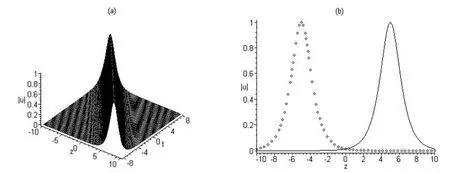
图6 与解u9的模对应的孤波结构及孤波随时间演化图（（a）取cg=1时随t变化的波形图；（b）取cg=1，t=-5（实线），t=5（虚线）时的波形截面图）

3 结论

借助于著名的齐次平衡原理和F-展开法的基本思想，研究了非线性双芯光纤方向耦合器中的脉冲传输所满足的非线性薛定谔方程组，得到了满足传输方程的多种显式精确行波解，其解包括了Jacobi第二类、第三类函数以及由它们组成的其它形式的周期波解和亮孤子解，并通过图形分析法，讨论了几种典型的特殊的周期波结构、孤波结构以及孤波随时间的演化。与以往的研究成果[4-7]相比，图3、图5所示的周期波结构随时间的演化是新的。在今后还将作进一步研究。

［1］MOLLENAUER LF,STOLEN R H，GORDON J P.Experimental observation ofpicosecond pulse narrowing and solitons in optical fibers［J］.Phys RevLett，1980，45（9）：1095.

［2］WANG M L，ZHOU Y B，LI Z B.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics［J］.Physics Letters A，1996，216（1）：67.

［3］LI BA，WANGML.Applications ofF-expansion method tothe coupled KdVsystem［J］.Chin PhysB，2005，14（9）：1698.

［4］MA Z Y，MA S H.Analytical solutions and rogue waves in（3+1）-dimensional nonlinear Schrdinger equation［J］.Chin Phys B，2012，21（3）：030507

［5］ZHU H P.Nonlinear tunneling for controllable rogue waves in two dimensional graded-index waveguides［J］.Nonlinear Dyn，2013，72（4）：873.

［6］DAI C Q，WANG Y Y，CHEN J L.Analytic investigation on the similariton transmission control in the dispersion decreasing fiber［J］.Opt Commun，2011，284：3440.

［7］WU X F，HUA G S，MA Z Y.Novel rogue waves in an inhomogenous nonlinear medium with external potentials［J］.Commun Nonlinear Sci Numer Simulat，2013，18（12）：3325.

Dynamic Behaviors of the Solutions in Nonlinear Optical Fiber Coupler Schrodinger Equations

WUXiaofei1,HUAGuosheng2
（1.FacultyofEngineering，Lishui University，Lishui 323000，Zhejiang；2.Center ofInformation Technology，Lishui University，Lishui 323000，Zhejiang）

In this paper，the F-expansion and homogeneous balance method are used to solve the nonlinear optical fiber coupler Schrdinger equations.With this method，many kinds of explicit and exact traveling wave solutions are acquired，including Jacobi doubly periodic solutions and bright soliton.Besides，the dynamic behaviors of some solutions are discussed by direct computer simulations

coupler Schrdinger Equations；F-expansion；bright soliton

10.3969/j.issn.2095-3801.2017.05.001

O411.1

A

2095-3801（2017）05-0001-07

2017-02-15；

2017-03-20

浙江省自然科学基金资助项目“非线性动力系统的狄拉克结构约化”（LY14A010005）

吴晓飞，女，浙江缙云人，教授，硕士。