RN上一类拟线性椭圆方程解的存在性

李桃桃，沈自飞

（浙江师范大学数理与信息工程学院，浙江金华321004）

RN上一类拟线性椭圆方程解的存在性

李桃桃，沈自飞

（浙江师范大学数理与信息工程学院，浙江金华321004）

研究一类拟线性椭圆方程

拟线性椭圆方程；扰动法；山路引理；正负解

0 引言

近年来，许多学者一直专注研究拟线性椭圆方程各种解的存在性问题，关于这类问题已经建立了一系列理论，如变量替换法、极小化约束法、Nehari流形法、扰动法，详细内容可参见文献［1-6］及其所附的参考文献。

在文［5］中，刘嘉荃等应用扰动法研究了方程

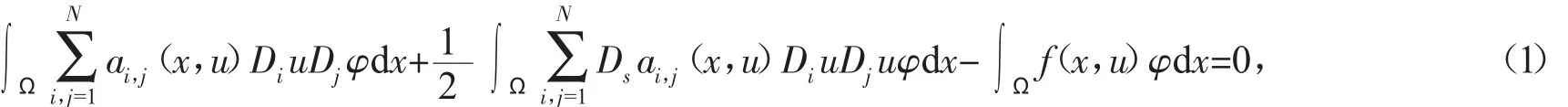
解的存在性问题，并证明了当f及ai，j满足适当的条件时，方程（1）存在正解、负解及一列变号解。其中，任意的φ∈C∞0（Ω），Ω是RN中具有光滑边界的有界区域，f：RN×R→R是超线性的且关于u次临界增长。

本文将考虑下列方程

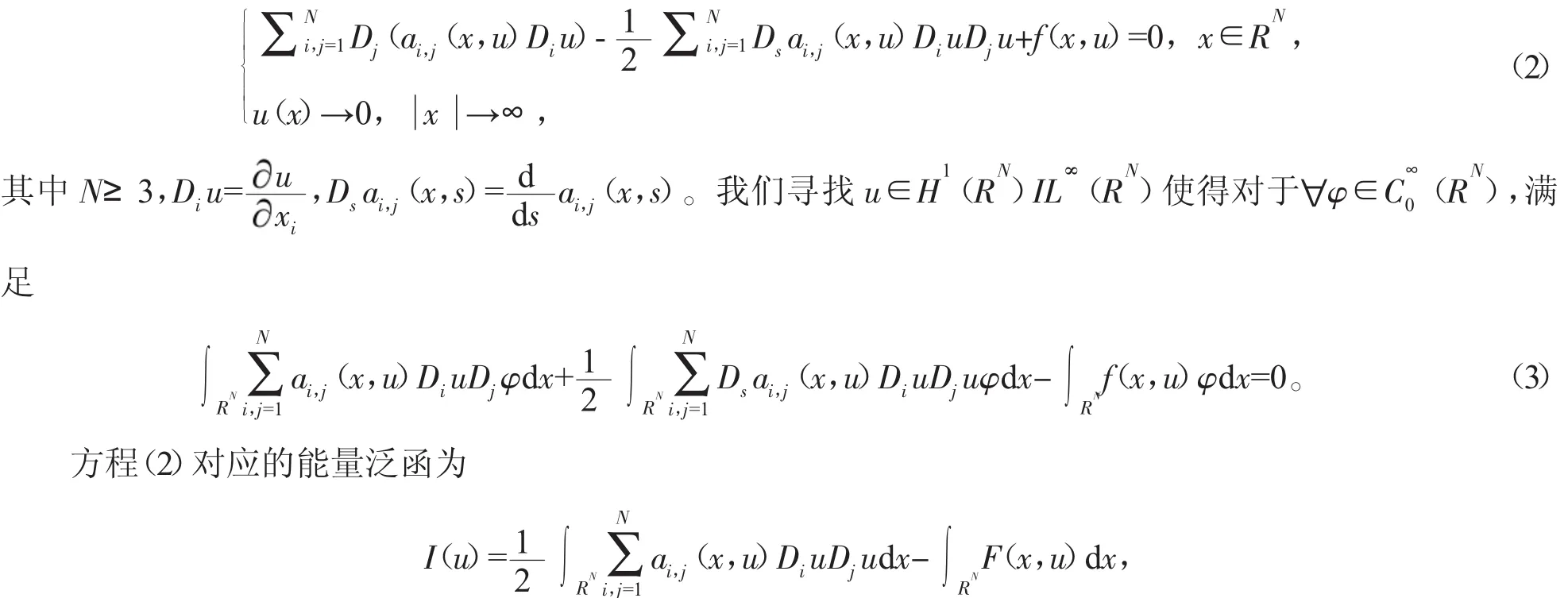
方程（2）中函数 f和 ai，j满足下列条件：

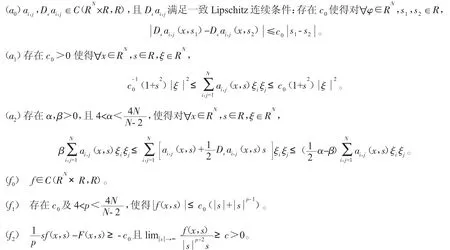
由于没有一个合适的空间使得方程（2）对应的泛函I既有光滑性又满足一定的紧性，为了克服这个困难，我们采用文［6］的方法，解决了泛函在无界区域上紧性的缺失。取 μ∈（0，1]，＜s＜min｛ 4，N ｝，我们考虑扰动问题通过寻找u∈X：=W1，（sRN）IH1V（RN）使得

1 引理

2 定理1的证明

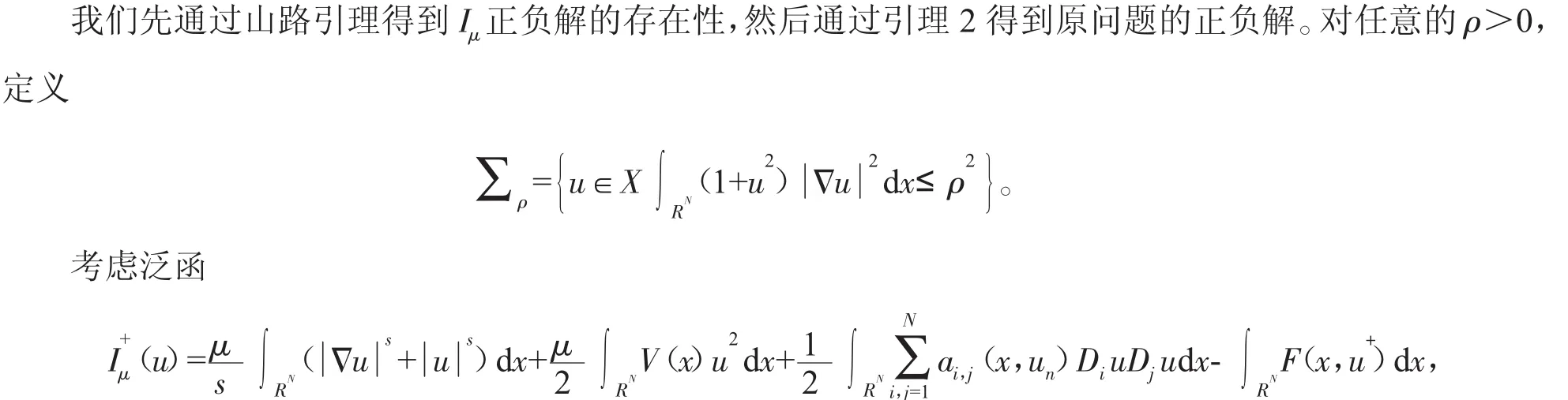
其中 u±=max（±u，0）。类似于引理 3，我们也可以证明 Iμ+也满足（PS）条件。由（f1）有

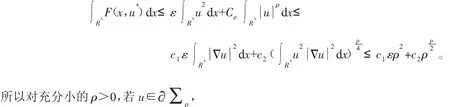
由山路引理可知，存在 0≤uμ∈X 使得 I+μ（uμ）=cμ。再由强极值原理可知 uμ是 Iμ的正临界点。从而有：

引理 4 存在常数 m1和 m2及 Iμ的正临界点 uμ使得 m1≤Iμ（un）≤m2。

定理1的证明 由引理4可知，存在常数m1和m2及Iμ的正临界点uμ使得m1≤Iμ（un）≤m2。由引理2 可知，存在 un→0 及 I的临界点 u∈H1（RN）I L∞（RN）使得 uμn→u 在 H1（RN）中，uμnuμn→uu 在 L2（RN）中，且 Iμ（n（Iu）。因此，u是I的临界点，即u是I的正解。类似地，我们可以证明方程（2）存在一个负解。

［1］COLINM，JEANJEANL.Solutions for a quasilinear Schr dinger Equation：a dual approach［J］.Nonlinear Anal，2004，56（2）：213.

［2］ZOUWM.Variant fountain and their applications［J］.Manuscripta Math，2001，104（3）：343.

［3］LIUJ Q，LIUYQ，WANGZQ.Quasilinear elliptic equations via perturbation method［J］.Proc Amer Math Soc，2013，141（1）：253.

［4］LIUJ Q，LIUYQ，WANGZQ.WANG，Quasilinear elliptic equations with critical growth via perturbation method［J］.J Differ-etial Equations，2013，254（1）：102.

［5］LIU J Q，LIU X Q，WANG Z Q.Multiple sing-changing solutions for quasilinear elliptic equations via perturbation method［J］.CommPartial Differential Equation，2014，39（12）：2216.

［6］LIU J Q，LIU X Q，WANG Z Q.Multiple solutions for quasilinear elliptic equations with a finite potential well［J］.J Differential Equation，2014，257（8）：2874.

The Existence of Solutions to a Quasi-liner Elliptic Equation in RN

LI Taotao，SHENZifei
（College ofMathematics，Physics and Information Engineering，ZhejiangNormal University，Jinhua 321004，Zhejiang）

In this paper，we consider the following quasi-liner elliptic equation whereN≥3has subcritical growth with respect to u.We prove the existence of positive solutions and negative solutions to the equation by using perturbation method and mountain pass theorem.

quasi-liner elliptic equation；perturbation method；mountain pass theorem；positive solution and negative solution

10.3969/j.issn.2095-3801.2017.05.003

O175.25

A

2095-3801（2017）05-0016-07

2017-03-06；

2017-05-02

国家自然科学基金资助项目“几类非典型薛定谔方程的变分方法研究”（11671364）

李桃桃，女，安徽安庆人，硕士生。