围长至少为21的平面图的邻和可区分的顶点列表色数

包一萍

（浙江师范大学数理与信息工程学院，浙江金华321004）

围长至少为21的平面图的邻和可区分的顶点列表色数

包一萍

（浙江师范大学数理与信息工程学院，浙江金华321004）

设f是从图G的顶点集合V到整数集合N的一个映射，令每一个点v的邻和为Sf（v）=Σu∈NG（v）f（u），若f满足任意相邻两点的邻和不相等，则称f是图G的一个邻和可区分的顶点列表标号。设L为图G的一个k-列表配置，对任意点v有f（v）∈L（v）。若存在最小的正整数k使得对任意L，图G都有一个邻和可区分的顶点列表标号f，则称k为图G的邻和可区分的顶点列表色数，ηl（G）。证明当平面图G的围长至少为21时，图G的邻和可区分的顶点列表色数ηl（G）至多为3。

顶点列表色数；权转移方法；组合零点定理

0 引言

对于图的邻和可区分的顶点列表标号，已经有许多的结论被证明[1-5]。在2009年，Czcrwinski，Grytczuk和Zelazny[1]提出了一个重要猜想：对于任意图G，有η（G）≤χ（G）。这个猜想仍未被证明。如果这个猜想是正确的，那么显然对于任意平面图G会有η（G）≤4。好多学者在平面图中研究邻和可区分的顶点列表标号，并且得到了一系列结果。现在已知的最好的上界是468[2]。针对3-可染平面图，文献［2］中有结论：若G是一个3-可染平面图，则有η（G）≤36。针对限定了围长最小值的平面图，文献［2］认为：任意一个围长至少为13的平面图G，有η（G）≤4。

本文主要研究的是限定了围长最小值的平面图的邻和可区分的顶点列表色数。这个问题最开始在2015年被Brandt，Diemunsch和Jahanbekam[4]研究，他们提出了以下结论：

定理 令G为围长是g的平面图。

（1）若g≥5，则ηl（G）≤19；

（2）若g≥6，则ηl（G）≤9；

（3）若g≥7，则ηl（G）≤8；

（4）若g≥26，则ηl（G）≤3。本文主要提出了如下结论：

定理1令G为围长是g的平面图。若g≥21，则ηl（G）≤3。

证明上述定理的方法主要为极小反例和权转移方法[6-8]。首先，我们主要介绍了一些利用组合零点定理[9]可以简化的构形。接着，我们证明了在极小反例中这些构形是不可避免的，最后利用权转移证明极小反例不存在，从而完成我们对定理1的证明。

1 可被k-简化的构形

图G被称作k-严格的。如果ηl（G）＞k且对任意非空顶点子集X，有ηl（G-X）≤k。若H是图G的一个导出子图，则把H和G中与H中的点相关联的边一起叫做图G的一个构形。称一个构形是可被k-简化的，如果在任意k-严格的图G中都不存在该构形。本章节主要介绍一些可被k-简化的构形。

对于V（G）的子集X，令NG（X）=∪v∈XNG（v），用E X][ 表示由X导出的子图G X][ 中的边集。令

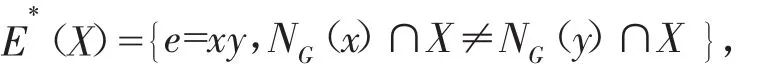
对于Z∈E*（X），用X[ Z ]表示与Z中某条边的某个端点相关联的X中的点构成的集合。

引理1 在图G中，令X为V（G）的一个子集，对于任意一条边e=wv∈E*（X），令若在P'X的展开式中存在一个度为 E*（X） 的满足 η（u）≤k-1的系数非零的单项式则 G 不是 k-严格的。

证明 假设G是k-严格的，L是G的一个k-列表分配，显然有L不是G的一个邻和可区分的顶点列表标号。因为G是k-严格的，所以G-X有一个邻和可区分的L-顶点列表标号f。对于任意的u∈X，令xu是一个表示u的标号的变量。对于E*（X）中的任意一条边e=wv，令其中ce是一个常数。令在G上的延拓是G的一个邻和可区分的L-顶点列表标号当且仅当PX（cu：u∈X）≠0。这里 PX（cu：u∈X）是在多项式 PX中令 xu=cu之后得到的式子。根据组合零点定理，若存在 cu∈L（u）使得 PX（cu：u∈X）≠0，则会有一个度为 E*（X） 的满足 η（u）≤k-1的单项式，其在PX的展开式中的系数非零。因为我们感兴趣的是在PX的展开式中度为 E*（X）的单项式的系数，所以在Qe中的常数ce可以被忽略。也就是说，度为 E*（X）的单项式在展开式P'X中的系数与其在展开式PX中的系数相同。因此根据我们的假设可以推出G有一个邻和可区分的L-顶点列表标号，矛盾。

引理2 假设V（G）的一个子集X导出一个二分子图（U，W），如图1。如果二分子图满足下列条件

2）对于任意边 xy∈E[ NG（ U）] ，有 NG（x）∩U=NG（y）∩U；对于任意边 xy∈E[ NG（ U）] ，有 NG（x）∩W=NG（y）∩W。

3）对于任意集合 Z∈E*（X），有Z ≤（k-1）X[Z]，则G不是k-严格的。

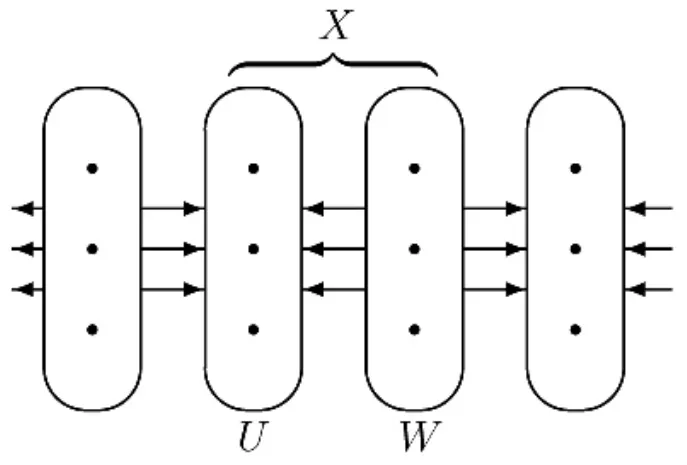
图1 可被k-简化的构形

证明 假设L是G的一个k-列表分配。如果G是k-严格的，则G-X有一个邻和可区分的L-顶点列表标号f。下面我们需要证明f可以被延拓成G上的一个邻和可区分的L-顶点列表标号。令f'为f在X上的延拓。对于满足条件2的任意边xy∈E[ NG（ U）]来说，有Sf（'x）-S（fx）=Sf（'x）-S（fy）。因为边xy对于f来说是好的，所以对于f'来说边xy也是好的。同理，对于满足条件2的任意边xy∈E[ NG（ W）]来说，xy对于f'均是好的。所以为了证明f'是存在的，我们只需要保证E*（X）中的边关于f'来说都是好的。

首先，在由边集E*（X）导出的子图中，给E*（X）的边一个定向，使得NG（U）中的点均为起点，NG（W）中的点均为终点。 若对于任意一条边e=vw∈E*（X），当边e的方向由v指向w时，我们令中每一个xu出现的正负性均相同（也就是说，xu均以-xu的形式在Qe中出现，或者均以+xu的形式出现在Qe中）。

又因为对于E*（X）中的任意子集Z，有Z ≤（k-1）X [ Z]，根据霍尔定理 [10 ]可以发现满足条件的映射π是存在的。

根据引理2，我们可以得到下述推论，推论1在 [ 4 ]中也有提到。

对于整数i＞1以及点v，令dG，（iv）=｛u∈NG（v）：dG（u）=i｝。如果边e=uv是一条割边，在G-e的连通分支中包含u的那一支是一棵树T，则称割边e是v的一条悬挂边，称连通分支T是v的一个悬挂分支。令σ（v）表示 v的悬挂边的数目，且令 β（v）=dG（v）- σ（v）。

推论 2 假设 G 是 3- 严格的，路 P=v1v2v3v4v5，满足 β（vi）=2（i=1，2，3，4，5），则 G 中不包含这样的路P。

证明 如果G中出现上述的路，运用引理2，其中k=3以及X=｛v2，v3，v4｝∪X（'X'是v1，v2，v3，v4和v5的悬挂分支的集合）。

推论3 假设G是3-严格的且C是G中一个长度至少为21的圈。如果C至少有16个β（v）=2的点v，且恰好有4个β（u）=3的点u，则C至少有两个β（w）≥4的点w。

证明 假设C中至多有一个β（w）≥4的点w。如果C中不存在β（w）≥4的点w，则运用引理2，其中k=3，X为C中β（v）=2的点v以及β（v）≤3的点v的悬挂分支的集合。否则，令w为C中β（w）≥4的唯一一个点，同样运用引理2，其中k=3，X为β（v）=2的与w不相邻的点v以及β（v）≤3的点v的悬挂分支的集合。

2 定理1的证明

定理1令G为围长是g的平面图。若g≥21，则ηl（G）≤3。

证明 假设上述定理不正确并令图G是点最少的极小反例。因此图G是连通的且非树（由于树的邻和可区分的顶点列表色数是2）。一条割边e叫做是必要的，如果G-e的每一个连通分支都包含一个圈。对于图G的任意一个点v，令E（v）E'（v）和E（v）分别表示与v相关联的边的集合，与v相关联的必要的割边的集合以及与v相邻的面的集合。令

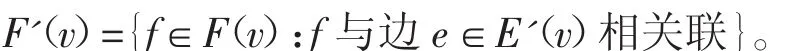
给每一个点v个初始权d（v）-4并且给每一个面f一个初始权（lf）-4，同时运用下述权转移规则。

R1 每一个1度点从它的邻点处接收1权并且从与它相关联的面处接收2权。

R3 每一个3度点v

R4 每一个有一个1度邻点的4度点v和每一个有两个1度邻点的5度点v。

根据欧拉公式[10]，在平面图中有如下等式

接下去我们只需证明根据上述权规则重新分配权后每一个点和每一个面的最终权至少为0，就可以得到矛盾。

根据权规则，每一个1度点从它的邻点和与它相关联的面处总共接收3权，每一个2度点从与它相关联的面处总共接收2权，每一个3度点v从与它相关联的面处接收1+dG，1（v） 权，但同时v又给它的1 度邻点 dG，1（v） 权，每一个4度点v从与它相关联的面处接收 dG，1（v）权，但v又给它的1度邻点dG，1（v） 权，每一个5度点v从与它相关联的面处接收max｛ 0，dG，1（v） -1 ｝权，但v又给它的1度邻点dG，1（v）权。因此5--点的最终权至少为0。

当d≥6时，一个d度点v给它的每一个1度邻点1权，因此v的最终权至少为

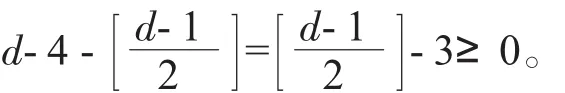
接下去仍需证明每一个面的最终权至少为0。为此，我们先证明引理3。对于面f，令V（f）和E（f）分别表示与f相关联的点的集合和与f相邻的面的集合。令

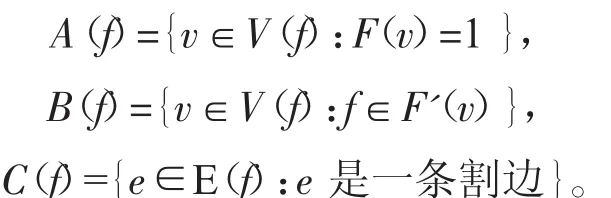
引理3 对于任意面f，有2 A（f） +B（f） ≤2 C（f） 。

证明 我们对 C（f） 进行归纳来证明结论。如果 C（f） =0，有 A（f） =B（f） =0，不等式成立。假设C（f）＞0和e=uv∈C（f）。用G'=G/e表示把边e收缩成一个点w之后得到的图。令f'=f/e。因为C（f'）=C（f）- ｛e ｝，所以有 C（f'）=C（f） -1。根据归纳假设，则有2 A（f'） +B（f'） ≤2 C（f'） =2 C（f）-2。

如果 ｛u，v ｝∩A（f）=｛u ｝，则有 A（f'）=A（f）- ｛u ｝和 B（f）=B（f'）；因此 2 A（f） +B（f） ≤2 C（f） 。

因为面f有一个长度至少为21的圈，并且每一条割边都在（lf）中计算2次，所以面f的长度（lf）≥21+2 A（f） +B（f） 。令R（f）=｛v∈V（f）：β（u）=2 ｝，则f的最终权是

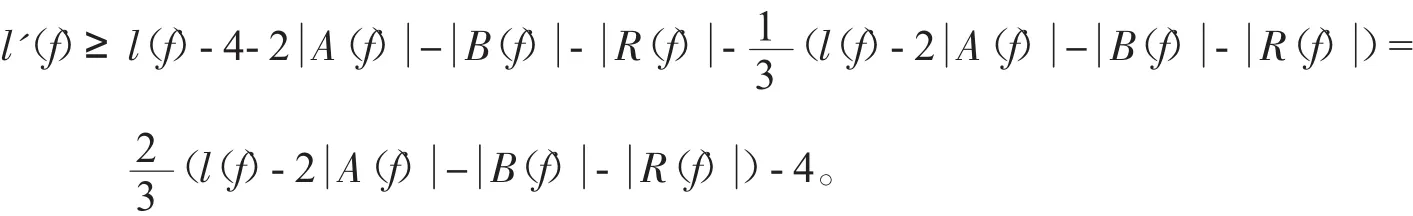
根据推论2，在一个圈中最多连续出现R（f）中的4个点，因此我们有 R（f） ≤4「（（lf）-2 A（f）-B（f））「。因为图G的围长g≥21，所以 （lf）-2 A（f） -B（f） ≥21。令d（f）=（lf）-2 A（f） -B（f） ，则

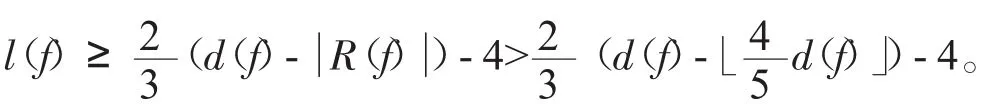
如果d（f）≥26，则l（'f）≥0。

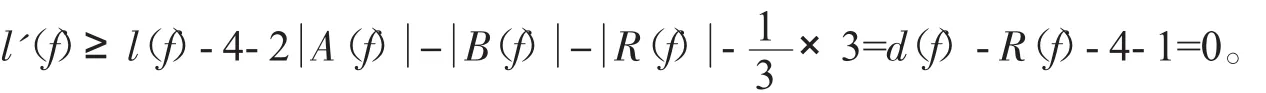
综上，定理1成立。

［1］CZERWINSKI S，GRYTCZUKJ，ZELAZNYW.Luckylabelings ofgraphs［J］.Informa Process Lett，2009，109：1078.

［2］BARTNICKI T，BOSEKB，CZERWINSKI S，et al.Additive colorings ofplanar graphs［J］.Graphs Combin，2012，30（5）：1087.

［3］AKBARI S，GHANBARI M，MANAVIYATR，et al.On the luckvchoice number ofgraphs［J］.Graphs Combin，2013，29：157.

［4］BRANDTA，DIEMUNSCH J，JAHANBEKAMS.Luckychoice number ofplanar graphs with given girth［EB/OL］.（2015-06-01）［2016-12-21］.http://math.ucdenver.edu/sjahanbekam/Lucky.pdf，2015.

［5］STEINBERGR，TOVEYC.Planar ramseynumbers［J］.J Combin TheorySer B.1993，59（2）:288.

［6］PRZYBYLOJ，WONGT.Neighbor DistinguishingEdge Colorings Via the Combinatorial NullstellensatzRevisited［J］.J Graph Theory，2015，80（4）：299.

［7］NORINE S，WONGT，ZHUX.Circular choosabilityvia combinatorial Nullstellensatz［J］.J Graph Theory，2008，59（3）:190.

［8］HUANGP，WONGT，ZHUX.Application of polynomial method toon-line list colouringofgraphs［J］.European J Combin，2012，33（5）：872.

［9］ALONN.Combinatorial Nullestellensatz［J］.Combin Prob Comput，1999（8）：7.

［10］WESTD.Introduction tograph theory［M］.USANJ:Prentice Hall Inc，1996：318-320.

The Lucky Choice Number for Planar Graph with Girth at Least 21

BAOYiping
（College ofMathematics，Physics and Information Engineering，ZhejiangNormal University，Jinhua 321004，Zhejiang）

A lucky labeling f of a graph G is a mapping which assigns to each vertex v a positive integer f（v），so that any two adjacent vertices have distinct neighbor-sums,where the neighbor-sum of a vertex v is Sf（v）=Σu∈NG（v）f（u）.The lucky choice number of G,ηl（G），is the smallest positive integer k such that for any k-list assignment L of G，G has a lucky labeling f with f（v）∈L（v）for each vertex v.In this paper，we prove that ηl（G）is at most 3 for every planar graph G with girth at least 21.

lucky choice number；discharging method；Combinatorial Nullstellensatz

10.3969/j.issn.2095-3801.2017.05.005

O157.5

A

2095-3801（2017）05-0030-06

2017-01-05；

2017-02-13

国家自然科学基金资助项目“图的圆环染色和分数染色”（11171310）

包一萍，女，浙江杭州人，硕士生。