一类具临界指数项非线性Choquard方程驻波解的稳定性

程志鹏

（浙江师范大学数理与信息工程学院，浙江金华321004）

一类具临界指数项非线性Choquard方程驻波解的稳定性

程志鹏

（浙江师范大学数理与信息工程学院，浙江金华321004）

研究一类带有临界指数项的非线性Choquard方程

驻波解的轨道稳定性。0＜μ＜3且p=2+（2-μ）/3。位势函数V（x）在合适的假设下且ω充分大时，能够得到驻波解u=eiωtφ的稳定性。

Choquard方程；驻波解；基态解；轨道稳定性

0 引言

近年来，很多学者对局部薛定谔方程进行了广泛的研究。在文献［1］中，对于局部薛定谔方程驻波解的轨道稳定性的相关结论有着详细的介绍。在文献［2］中，作者得到了方程在临界指数情形下方程驻波解的稳定性，其中ω＞0。而对于非局部问题，近年来许多学者研究了方程

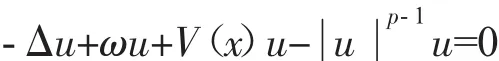
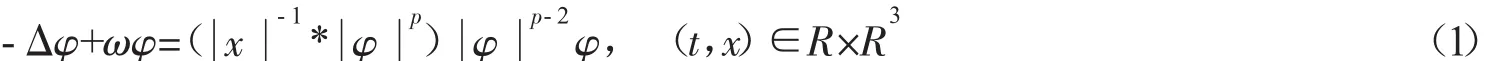
解的存在性问题。在文献［3］中，作者研究了当p=2时方程（1）基态解的存在性，以及在H1（R3）中存在唯一的正径向解。在文献［4］中，利用径向解的唯一性，作者研究了p=2时方程（1）驻波解的稳定性。对于非局部问题在临界情形下的一些结果以及其他非局部问题驻波解的稳定性，读者可以参见文献［5-6］。

本文考虑方程

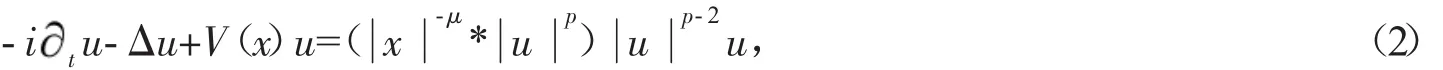
当 0＜μ＜3，p=2+（2-μ）/3 时，如下形式驻波解的稳定性：

其中ω＞0，φ∈H1（R3）｝｛。由式（3），φ满足非局部椭圆方程：

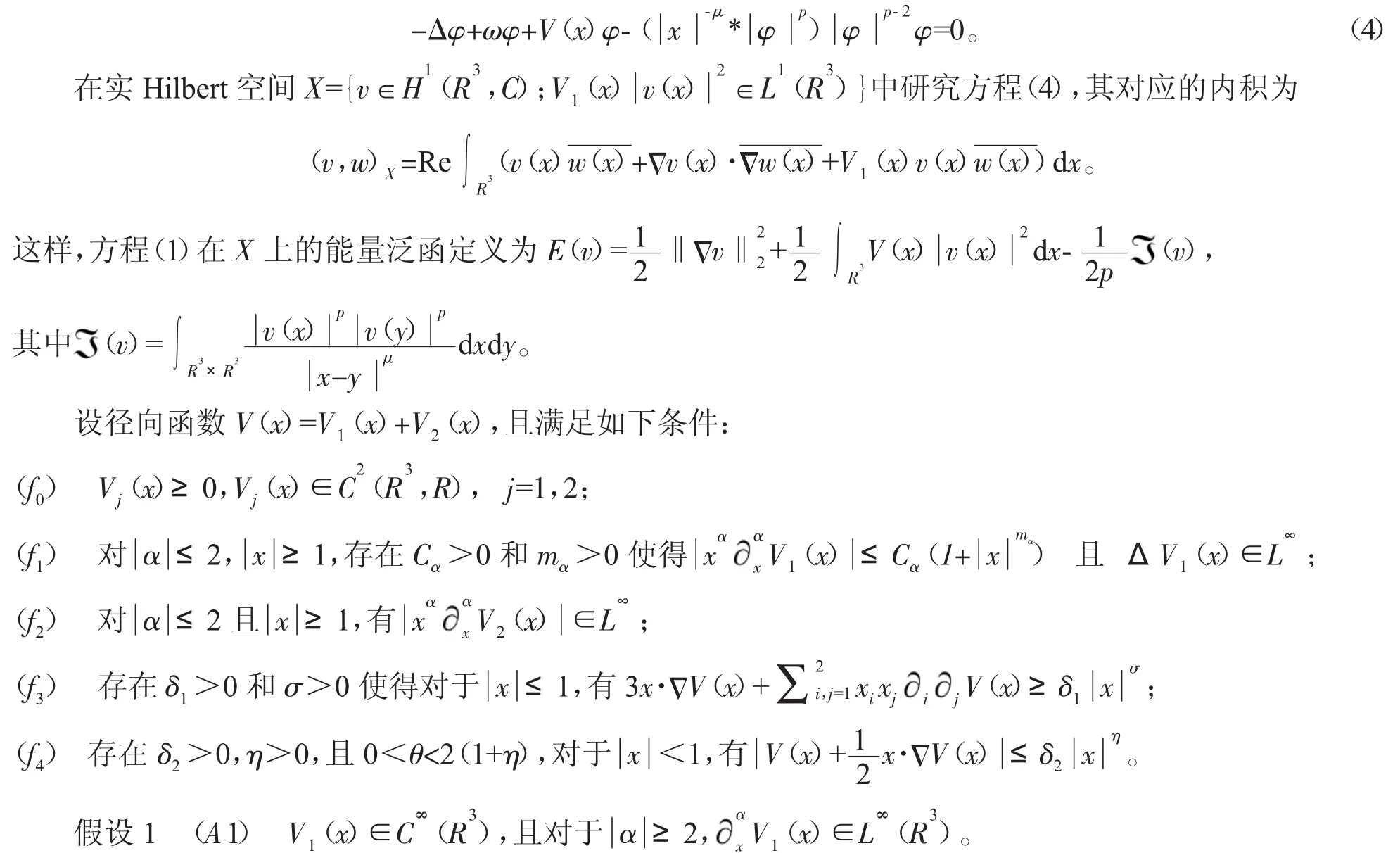
由文献［7］所述，如果有条件（f0）成立，且 V1（x）还满足上面的假设条件（A1），则可以得到方程（2）Cauchy问题的局部适定性：

命题 1 （P1） 对任意的 u0∈X，存在 T=T（‖u0‖X）＞0，且方程（2）有唯一的解 u（t）∈C（［0，T］，X），这里 u（0）=u0满足

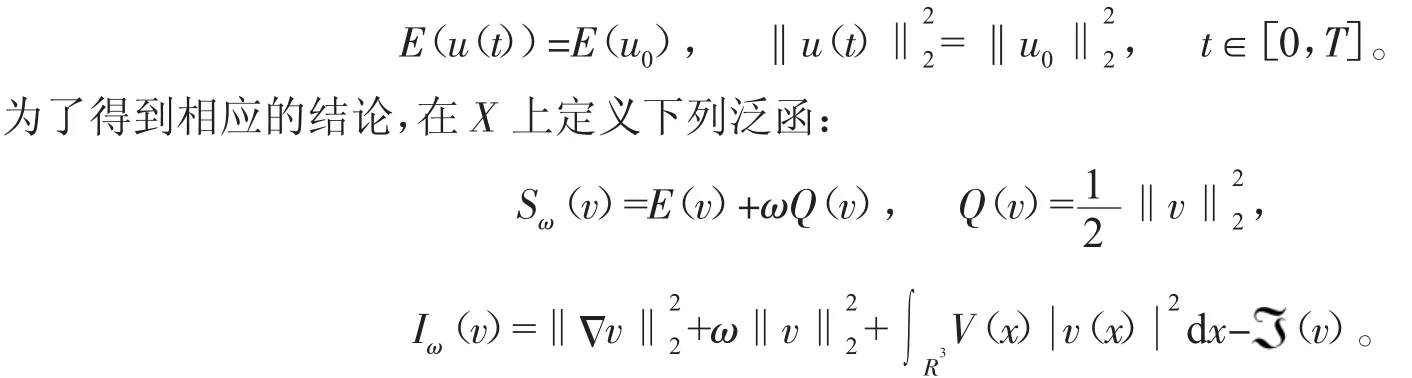
考虑接下来的极小化问题

其中

记基态解的集合为

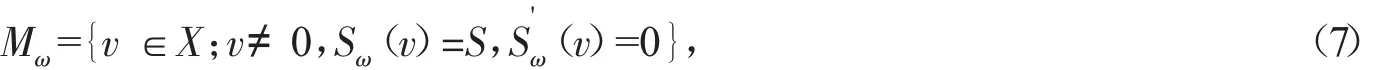
且Mω是非空的。若φω∈Mω是方程（2）的基态解，则有下列命题：

命题 2 （P2）（见文献［2］）φω（x）∈W2，（rR3）且 φω（x）∈C2（R3）。

定义 对于 φω∈Mω，如果对任意的 ε＞0，存在 δ＞0 使得 infθ∈R‖u（0）-eiθφω‖X＜δ，那么对任意的 t≥0且 u（0）=u0，方程（2）的解 u（t）满足‖u（t）-eiθφω‖X＜ε，则方程（2）的驻波解 eiωtφω在 X 中是稳定的；否则，eiωtφω在 X 中不稳定。

定理 1 对于 φω∈Mω且 0＜μ＜3，p=2+（2-μ）/3。若条件（P1），（P2），（f0）～（f4）均成立，则存在 ω0∈（0，∞）使得 S"ω（φω）＞0，对任意的 ω∈（ω0，∞），方程（2）的驻波解 eiωtφω是稳定的。

1 引理

由φω∈Mω且Iω（φω）=0，经计算可得

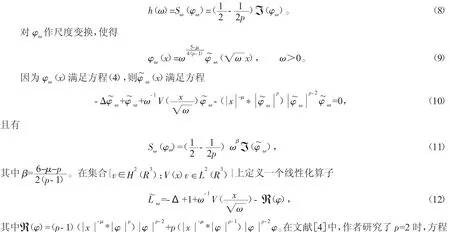
（1）驻波解的轨道稳定性。在此工作的基础上，对于一般的p，在R3中利用Hardy-Little-Sobolev不等式，许多学者得到5/3＜p＜7/3时，方程（1）基态解的存在性，并且已经得到了在p=2的一个很小的邻域内方程（1）径向解的唯一性。对更一般的情形，假定有如下命题：

命题3 当V（x）=0且ω=1时，方程（4）变为

当 μ=1，p=7/3；μ=2，p=2 时，方程（13）也存在唯一正的径向解。

引理1对φω∈Mω，若p=2+（2-μ）/3。由命题3，ψ1（x）是方程（13）唯一的正径向解。～φω（x）由（9）式定义，则有

证明 详细的证明参见文献［4］引理3.1和3.2。

引理 2 （［5］命题 2）对 φω∈Mω，若 5/3＜p＜7/3 且条件（P2），（f0）～（f2）均成立。ψ1（x）是方程（13）唯一正的径向解。则

1）当r→∞，φ～（r）→0；

ω

2）存在C0＞0，r0（p）＞0且 ω1（p）＞0，使得对任意的r≥r0，ω≥ω1，有 φ～ω（r） ≤C0r-1e-r/2；

3）对充分大的 ω，ωα，φ～ω是（0，∞）到X的C1映射

4）对于充分大的 ω，Lω可逆，且Lω是有界的。即存在 ω1＞0，C1＞0，使得对任意的 ω≥ω1，有‖Lωv‖2≥C1‖v‖2，其中 v∈H2（R3）且 V（x）v∈L2（R3）。

注 与文献［2］命题2有所不同的是，这里要将文献中的局部项改为非局部项来证明引理2，其余的证明同文献［2］。

引理 3 （Fubini）假设 F∈L1（R3×R3），那么对几乎处处 x（或 y）∈R3，F（x，y）∈L1y（x）（R3）且 ∫3F（x，y）

R

dy（x）∈L1y（x）（R3），并且有 ∫3dx∫3F（x，y）dy=∫3dy∫3F（x，y）dx。

RRRR

2 稳定性

证明定理1 用反证法，假设eiω1tφω1在X中不稳定。由稳定性的定义可知，存在 ε0＞0，初值uk（0）∈U1/k（φω1）使得其中 uk（t）是方程（1）的解。而在某一时刻 tk，uk（tk）满足

因为E和Q是关于t不变的，令uk（tk）=vk，当k→∞时，有

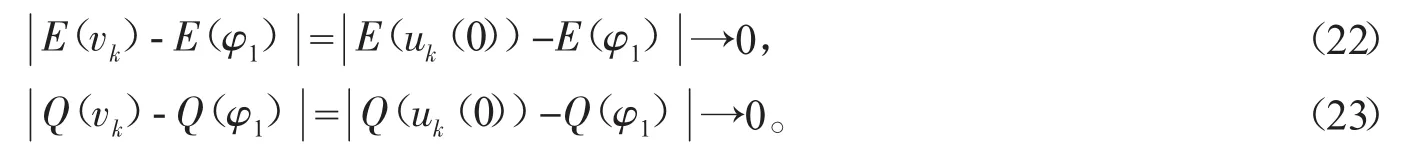
由（21）可知‖vk‖X有界。因为ω（u）是连续的，所以ωk=ω（vk）关于k有界。选择δ充分小使得引理7成立，则有

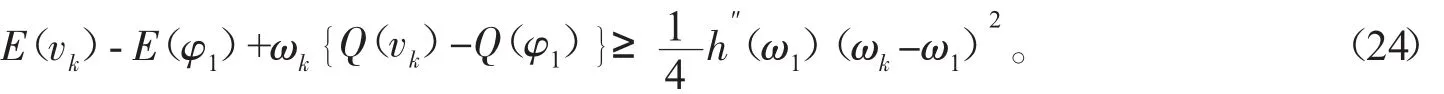
因为h（"ω1）＞0，则limωk=ω1。因为 h（·）是连续的，由式（8），得到

k→∞

当 k→∞，由（22）和（23）可得

因此，由（25）和（26），当 k→∞ 时，Sω（1wk）→h（ω1）。其中 wk=（（φ1）/（vk））vk，这样，当 k→∞，（wk）=（φ1）且‖wk-vk‖→0时，存在序列 ｛θk｝使得‖wk-eiθkφ1‖X=0。即lim‖vk-eiθkφ1‖X=0，这与（21）是矛k→∞盾的。

［1］STUARTC A.Lectures on the Orbital StabilityofStandingWaves and Application tothe Nonlinear Schrdinger Equation［J］.Milan Journal ofMathematics，2008，76（1）：329.

［2］FUKUIZUMI R.Stability of standing waves for nonlinear Schrdinger equations with critical power nonlinearity and potentials［J］.Advances in Differential Equations，2004，10（3）：259.

［3］LIEBEH.Existenceanduniquenceoftheminimizingsolutionofchoquard’snonlinearequation［J］.StudiesinAppliedMathematicals，2002，57（57）：93.

［4］CAOP，WANGJ，ZOUW.On thestandingwavesfornonlinearHartreeequation with confiningpotentia［lJ］.JournalofMathematical Physics，2012，53（3）：033702.

［5］CAZENAVE T，LIONS P L.Orbital stability of standing waves for some nonlinear Schrdinger equations［J］.Communications in Mathematical Physics，1982，85（4）:549.

［6］CHENJ，GUOB,HANY.Sharp contrast in nonlocal inequalityand its applications tononlocal Schrdinger equation with harmonic potentia［lJ］.Communications in Mathematical Sciences，2009（7）：549.

［7］CAZENAVE T.Semilinear Schrdinger Equations［M］.NewYork：Courant Lecture Notes in Mathematics，2003：635.

The Stability of Standing Wave for Nonlinear Choquard Equation with Critical Power Nonlinearity and Potential

CHENGZhipeng
（College ofMathematics，Physics and Information Engineering，ZhejiangNormal University，Jinhua 321004，Zhejiang）

We studied the stability of standing wave solution for nonlinear Choquard equation where 0＜μ＜3 and p=2+（2-μ）/3.The stability of the standing wave u=eiωtφ is well derived under the suitable assumptions on the potential V（x）and appropriate frequency ω.

Choquard equation；standing wave solution；ground states；orbital stability

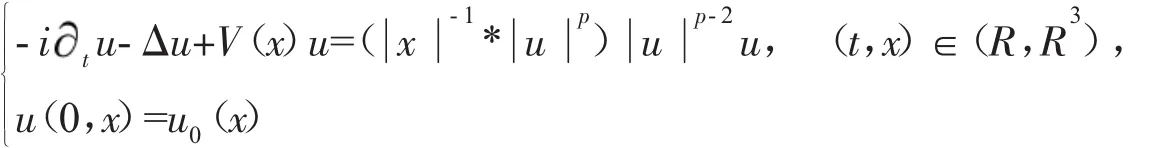
10.3969/j.issn.2095-3801.2017.05.004

O175.25

A

2095-3801（2017）05-0023-07

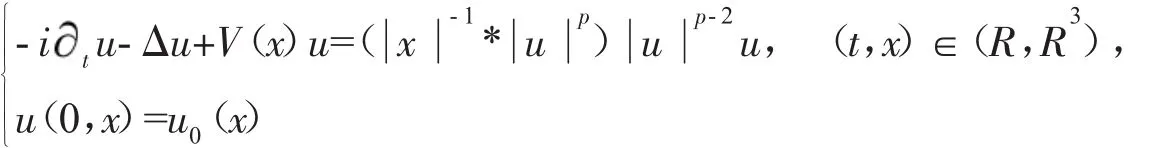
2016-11-07；

2017-01-05

浙江省自然科学基金资助项目“非线性Choquard方程与Dirac方程的奇异扰动问题”（LY15A010010）

程志鹏，男，安徽安庆人，硕士生。