对一道北京卷高考题的疑惑、解惑及另解发散

新疆乌鲁木齐市实验中学 强少华

对一道北京卷高考题的疑惑、解惑及另解发散

新疆乌鲁木齐市实验中学 强少华

2009年高考北京卷中有这样一道题：点P在直线l：y=x-1上，若存在过P的直线交抛物线y=x2于A,B两点，且|PA|=|AB|，则称点P为“β点”，那么下列结论中正确的是（）A.直线l上的所有点都是“β点”；B.直线l上仅有有限个点是“β点”；C.直线l上的所有点都不是“β点”；D.直线l上有无穷多个点（不是所有的点）是“β点”。

本题主要考查阅读与理解、信息迁移以及学生的学习潜力，考查学生分析问题和解决问题的能力，属于创新题型。

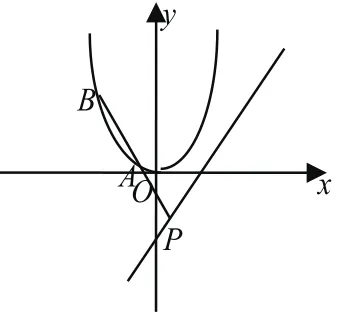
参考答案：如图，设A（m，n），P（x，x-1），则点B（2m-x，2n-x+1）。∵A、B在抛物线y=x2上，

1.疑惑：学生在做这道题时，笔者发现除了这种解法，学生还有一种典型解法：

∵点A在抛物线上，整理得

从而导致学生选B或D。(简单分析，第二种解题思路与参考答案没有任何区别，x1确实也没有其他限制，但为什么会出现这样两种截然不同的结果呢？)

2.解惑：用数形结合思想仔细分析，在参考答案中，若固定点A,动态来看，在直线l上一定存在点P,使得,故可用此方法。但第二种解法是根据PB中点A一定在抛物线上后,把点A的坐标代入抛物线方程得到。题中若存在点P满足是否就一定说明对任意的点B,PB的中点就一定在抛物线上呢？答案是否定的。如图，比如在直线上任取一点P,过P作抛物线的切线，切点假设是B,则PB的中点B一定不在抛物线上,故代入进去，肯定Δ＞0不恒成立。这也正好解释了为什么第二种解法会出现这样的结果。

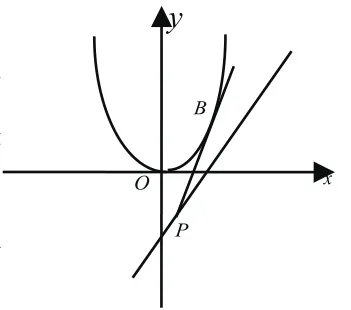
3.另解：疑惑解决了，笔者想到，作为一道选择题，按照参考答案的解法花的时间太长，而这道题出题人的意思是不是考查学生的数形结合能力呢？如果在直线l上任取一点P，过P作抛物线的切线，切点是A,然后将该直线绕点P旋转一定角度，产生的弦的长由零逐渐增大，则一定可以在抛物线上找到一点B,使得故答案选A。

4.发散：其实，在高中的数学学习中经常会遇到这类问题。例如：若椭圆与抛物线有公共点，求实数a的取值范围。很多学生看到这道题，就会想到联立方程由Δ≥0得到范围为但事实上这是等价的吗？画出这两个曲线的图象，易知Δ=0是抛物线与椭圆相切的情形，当抛物线沿轴向下平移至与抛物线相切时，再继续向下平移时就没有公共点了，数形结合就可以看出答案应是

另外，在解决某些三角问题时，如果我们多考虑一下它的几何意义，有些问题会有很多奇思妙解。例如：方程有解，求a的取值范围。不管是学生还是老师，都喜欢用辅助角公式化简，然后利用三角函数的有界性来处理。