关注课堂提问,彰显学科魅力
江苏省淮安市金湖县第二中学 严永平
关注课堂提问,彰显学科魅力
江苏省淮安市金湖县第二中学 严永平
提问作为教学不可或缺的部分,在课堂上占据重要地位。有效的提问不仅能激发学生兴趣,活跃课堂,拓展思维,还能突出学生主体,增强互动,改善关系。康托尔说过:“在数学领域中,提出问题的艺术比解答问题的艺术更为重要。”因此,要加强重视,精心设计,借助问题驱动教学,让学生在兴趣的牵引下主动参与,积极思考,促进问题的解决。
高中数学;课堂提问;设计
在传统教学中,大部分教师受到应试制度的影响,普遍存在“重成绩”的问题,过分关注学生分数,忽视了自身在教学中的引导作用,导致学生思维、能力发展受阻,学习兴趣下降,甚至产生抵触心理。对此,教师要深刻反思,积极转变,树立“以生为本”的教学理念,围绕学生设计教学,重视课堂提问,加强课堂引导,为其营造良好的学习氛围,以此促进其素养的提升。
一、启发性提问,激发探究兴趣
随着新课改的深入,素质教育观念普及,创新教育得到了普遍认可。为了提高数学教学的有效性,在设计时可将授课内容与创新教育理念结合,引入启发性提问,借助问题驱动学生,充分调动其积极性,让其在兴趣的牵引下主动参与,积极思考,促进自身能力的挖掘,在解决问题、自我提升的同时,给数学课堂增添活力。
如在教学“柱、锥、台和球等结构特征”的内容时,课标要求学生能借助实物概括出其几何特征,在语言描述特点的基础上进行分类。为了落实这一目标,我就结合学情设计问题,采取多种方式引导学生,确保其认知、理解到位,达到预期的目标。首先,我借助多媒体向学生展示空间物体图片,在唤醒其认识后,我就提出问题:“在日常生活中,哪些物体与其结构相似?”以此启发学生,让其运用生活经验思考问题。学生从身边事物着手,如教室里的梁柱、桌上的杯子以及生活中的各种物体等,由此便激发了其认知兴趣。独立思考过后,我让同桌交流,将自己的发现与他人分享,在此过程中促进思维碰撞,培养学生独创思维。交流过后,我让同学开展班级讨论,鼓励学生发表看法,说说自己的发现,或者提出疑问,共同探讨,解决问题,最大化地调动学生兴趣,让其主动融入,积极探索。
通过启发性问题的导入,给学生创设了生动的问题情境,不仅有利于其兴趣的激发,主动参与到课堂活动中,还激活了其思维,鼓励其创新思考,深入思考,为难点突破奠定基础,以此提升学习效果,达到预期目标。需要注意的是,在这一过程中,要密切关注学生动态,根据其认知发展灵活引导,推动教学的顺利展开。
二、层次性提问,提高参与意识
在传统教学中,教师惯用“一刀切”的模式,以统一的标准衡量学生,问题设计毫无区分度,无论是能力好的学生还是能力稍欠的学生,都“一视同仁”,让其解决相同的问题。时间一长,就出现了“优等生吃不饱,差等生吃不了”的问题,不仅影响教学效果,而且弱化了学生的参与意识。对此,就要注重问题层次,紧扣难点分层设计,满足不同程度学生的发展需求。
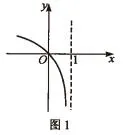
如一般在讲函数问题时,要数形结合,图像问题是最为普遍的,如这一题:若函数y=f(x)的图像如图1所示,那么函数y=f(1-x)的大致图像是( )。
这一题是让学生求函数图像,如果直接让其画出,难度较大,所以为了有效解决,我就设计层次性问题,由浅到深、由易到难地引导,循序渐进,促进学生理解,以此帮助其理解函数图像:
(1)函数y=f(x)的图像经过怎样的变化能得到函数y=f(-x)的图像?
(2)函数y=f(-x)的图像经过怎样的变化能得到函数y=f(1-x)的图像?
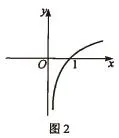
借助这两个问题的铺垫,学生层层剖析,步步深入,得到了图2,顺利解决了问题。可见,层次性问题的运用能将复杂的问题简化,帮助学生思考,让其不断深入,突破难点,有效解决问题,与此同时,在参与学习的过程中了解自身不足,查漏补缺,促进知识体系的完善。
三、探索性提问,培养思维能力
问题是思维的起点,探索是数学的生命,借助探索性问题引导,不仅能激发学生的探知欲望,让其化被动为主动,积极思考,还能明确探究方向,有目标、有计划地分析,不断提升思维。具体实施时,为了提高有效性,投放问题前我们要做好准备工作,反复钻研,将问题研究透彻,尝试预设学情,以便灵活应对,达到预期的培养目标。
如空间几何是高中数学教学的难点,也是很多学生的短板,由于空间想象能力的缺乏,在面对这类问题时,学生难以灵活应对。针对这一问题,我就会结合具体内容设置探索性提问,引导学生想象、探索,在深入挖掘的过程中掌握技巧,促进思维能力的培养。以这一题为例:设四面体ABCD的各棱长均相等,E、F分别是AC、AD的中点,则△BEF在该四面体的面ABC上的射影是( )。
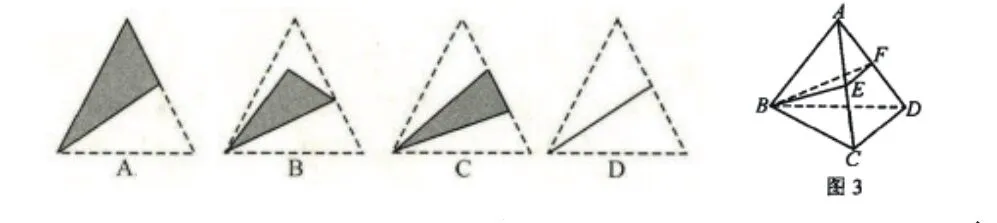
这一题难度较大,在讲解时我会引导其执因索果,由空间到平面,直观了解。首先,我让学生借助想象画出符合的正四面体,如图3所示。然后以此为对象,根据题目要求层层破解,因为几何体是正四面体,所以D在面ABC上的射影是其中心,由此得出AD在面ABC上的射影,因而选择答案B。由此,学生便在探索性问题的引导下自主探究,深入分析,逐步掌握空间几何题的解题技巧,促进自身想象思维的发展。
总之,课堂提问的优化是促进高中数学教学的有效途径,作为一门教学艺术,其对于课堂的重要性不言而喻。具体设计时,要结合实际,充分发挥学生的主体作用,采取多元化的引导方式,在满足学生需求,促进其思维发展的同时提高教学效率,给课堂增添魅力。

