在概率论与数理统计教学中融入数学建模思想的实践

贵州省贵阳学院 尚兴慧

在概率论与数理统计教学中融入数学建模思想的实践

贵州省贵阳学院 尚兴慧

众所周知，数学建模对于学生创新能力和创造性思维的培养有着十分重要的影响，同时还能极大地提高学生的学习兴趣，而且会给学生带来一种全新的思考思路。因此，在概率论的学习中融入数学建模的思想是十分必要的，这篇文章里就主要讲述了在概率论与数理统计中融入数学建模思想的重要意义和实践。

高等教育；概率论与数理统计；数学建模；实践

一、概率论与数理统计和数学建模思想的概念

1．概率论与数理统计的概念

简单地说，概率论与数理统计是对生活中发生的事情进行统计并计算其概率，最后归纳出系统的计算方法的学科。在本科院校里，这门学科已经成为学生学习的重要学科，并且在高等数学中占据非常重要的地位。这门学科的最重要特点就是全方面应用，在社会生产实践、社会科学、自然科学、教学实验、化学统计、物理探究、军工行业、工农业生产劳作中，概率论与数理统计的统计方法都发挥着重要的作用。

2．数学建模思想的概念

数学建模思想是通过运用数学学科工具和熟练地运用计算机相关技术，将我们要解决的实际问题转化成合理的数学模型，在运用数学原理的方法将其进行解决，这种解决问题的途径是十分方便的。在最近几年里，数学建模大赛都是比较热点的话题，竞赛题目包含了生活中的各个方面，这样能够方便我们解决日常生活中出现的问题。在进行数学建模之前，要对实际的问题进行多方面的考察，并进行统计分析，最后将实际问题具体化，再经过数学方法的计算得出实际结果。因此，这样有利于学习的学习方法应该被重视，而且还应该应用到概率论与数理统计的学习中去。

二、数学建模思想融入概率论与数理统计学习中的意义

1．提高学生学习兴趣和课堂效率，活跃课堂气氛，解决实际问题

由于概率论与数理统计是对事件的随机发生概率进行统计，因此这门学科所涵盖的内容也是十分抽象的，这就造成了课堂的学习是十分枯燥的，再加上在以前的学习中，学生对于这门课程的接触是比较少的，要想在短时间内学习并掌握好这门学科是十分困难的，所以老师在教学的过程中也是对学生进行填鸭式的灌输，这样就会在很大程度上降低学生学习的效率、学习兴趣和老师教学的热情。但是我们将数学建模思想融入概率论与数理统计中以后，老师在讲课的时候可以用计算机技术给学生展示模型图片以及模型的生成过程，这样同学们就会被这些生活的模型图片吸引，就可以在很大程度上提高学生的学习兴趣，还能不断活跃课堂的气氛，这就十分有利于知识的传授。

2．增加老师的知识储备，有利于教师能力的提升

在数学建模思想成功融入概率论的学习之前，老师需要学习很多知识，例如实际模型的寻找和计算机技术绘图的完成。同时，数学建模需要长时间进行不断的探索和实践，在这些过程中，一旦遇到不会的、不熟悉的知识，就都需要老师先学会，这对老师教学能力的提升和知识的储备都有十分重要的影响。

三、数学建模思想成功融入概率论与数理统计的实例

一般来说，数学建模分为以下几个步骤：

（1）表述。根据建模目的和信息，将实际问题转化为数学问题；

（2）求解。根据题目所传达的信息，选择适合题目的数学模型和方法；

（3）解释。将数学语言表述的解答转化为实际对象；

（4）验证。验证解题过程是否正确。

1．利用教材中的例题进行数学建模

在课本里，我们经常遇见许多的例题。例如我们经常遇见的生日问题：

问题背景描述：在100个人的团体中，如果不考虑年龄的差异，研究是否有两个以上的人生日相同。假设每人的生日在一年365天中的任意一天是等可能的，那么随机找n个人（不超过365人），求这n个人生日各不相同的概率是多少？从而求这n个人中至少有两个人生日相同这一随机事件发生的概率是多少？

实验目的：用计算机求解概率计算问题；当幂方次数较大时，用多项式拟合方法确定求概率的近似计算公式；了解随机现象的计算机模拟技术。

实验原理与数学模型： 这是一个古典概率问题，n个人中每一人的生日都可能在365天中的任何一天，样本空间中样本点总数为365n，考虑n个人的生日两两不同，第一个人的生日可能在365天中任一天，第二个人的生日不能与第一个人生日相同，第二个人的生日可能在364天中任何一天，类推可得，n个人生日两两不同的这一事件总有365×364×……×（365-n+1）个。

故这n个人的生日各不相同的概率（可能性）可由下面公式计算：

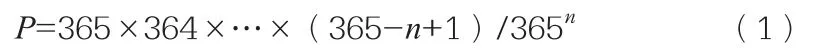
因而，n个人中至少有两人生日相同这一随机事件发生的概率为：

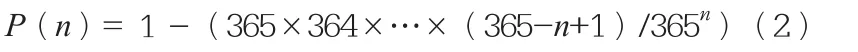
但是在利用公式进行计算时,所用的乘法次数和除法次数较多,可以考虑用多项式做近似计算。其实这个推广的过程就是一个建模的过程，在这个过程中，学生通过自己的实践得到了答案。

2．利用学生感兴趣的问题进行建模

各类标准化考试都有一些选择题，一般是每道题有 4 个可供选择的答案，其中只有一个是正确的。例如目前的高考和四六级考试都是人们关注的热点，而在这些考卷中都会有较多的选择，因此我们要想知道靠运气是否能够通过四六级，只需要计算概率就可以了，通过计算我们发现此概率为小概率事件，其概率之小，小到 1000 亿碰运气的人中，只有 0.874 人通过考试。

数学建模思想在概率论与数理统计中的成功应用，对于学生创新能力的提高和创新思维的发展都有十分重要的意义，这样做不仅能够很好地增加课堂的趣味性，还能有效提高学生学习的效率，有利于学生对于知识的掌握。在课程改革的背景下，不断地对课程进行创新是十分有必要的。不过最重要的还是要学生自己能够掌握好教师教授的知识，同时还应该不断地提高自身的各项能力。

[1]张二艳，董文乙．在概率论与数理统计教学中融入数学建模的探讨[J]．国家林业局管理干部学院学报，2012（2） ：40-43．

[2]亢婷．在概率论与数理统计教学中融入数学建模思想的研究——以应用型本科院校为例[J]．现代职业教育，2016（16）：88-89．

[3]李静．在概率论与数理统计教学中融入数学建模思想的探索[J]．数字化用户，2017（13）．

尚兴慧，女，1963年11月生，云南文山人，大学本科，副教授，研究方向：概率统计，邮编：550002。）