一类到圆锥曲线顶点距离有关的最值问题

浙江省三门第二高级中学 叶 挺

一类到圆锥曲线顶点距离有关的最值问题

浙江省三门第二高级中学 叶 挺

一、椭圆上和其短轴的一个端点距离最大的点位置问题

解：设动点B(x，y)，

消去x得：

这是一个关于y的二次函数，

其中y∈[-b，b]，对称轴方程：

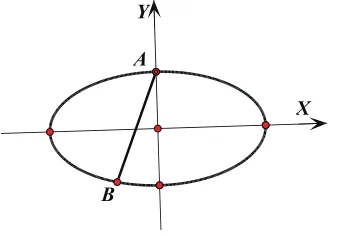
图1

结论1：当b≥c，即离心率为时，椭圆上和其短轴的一个端点距离最大的点在短轴的另一个端点处；当b＜c，即离心率为时，椭圆上和其短轴的一个端点距离最大的点在短轴的两侧。

（1）求直线y=kx+1被椭圆截得到的弦长（用a，k表示）；

（2）若任意以点A（0，1）为圆心的圆与椭圆至多有三个公共点，求椭圆离心率的取值范围。

分析（2）：点A（0，1）为椭圆短轴的一个端点。由对称性知，如图2，若圆与椭圆在y轴的左侧有两个公共点，则它们会有4个公共点，不满足条件；故圆与椭圆在y轴的左侧最多有一个交点，记B为圆与椭圆的一个公共点，如图3，则半径AB长随着B点从A点移动到（0，-1）过程中是单调递增的，即椭圆上和其短轴的一个端点距离最大的点在短轴的另一个端点处，由结论1知：离心率的取值范围是

二、抛物线上和其对称轴上的一个定点距离最小的点位置问题

O为坐标原点，记A(a，0) ，B为抛物线上的动点，求AB距离最小值。

解：设动点B(x，y)，则，

消去y得：|AB|2=x2+（2p-2a）x+a2。

这是一个关于x的二次函数，其中x∈[0，+∞]，对称轴方程：x=a-p。

（1）当a-p≤0，即a≤p时，B点在位置（0,0）处，AB距离最小；

（2）当a-p＞0，即a＞p时，B点在位置（a-p，±处，AB距离最小。

图2

图3

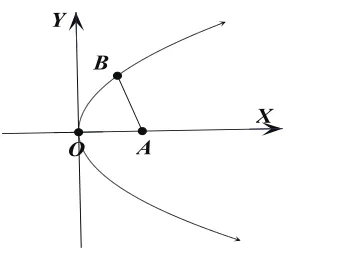
图4

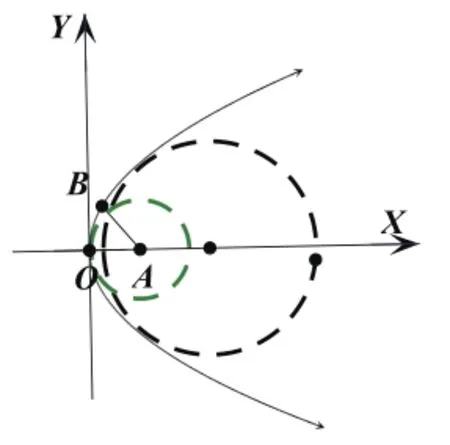
图5

结论2：当a≤p时，抛物线上到定点A(a，0)距离最小的点在顶点；

当a＞p时，抛物线上到定点A(a，0)距离最小的点在对称轴的两侧。

结论应用：如图6所示，酒杯的杯体轴截面是抛物线x2=2py（p＞0）的一部分，若将半径为r(r＞0)的玻璃球放入杯中，可以触及酒杯底部（即抛物线的顶点），则r的最大值为_________ 。

分析：由图给出的数据得抛物线的标准方程为：x2=2y，p=1。

玻璃球可以触及酒杯底部，等价于球心到抛物线顶点的距离是球心到抛物线上所有点的距离中的最小值。由结论2知：a≤p，即r≤1，则r的最大值为1。

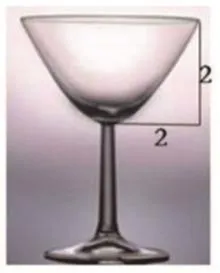
图6