制动盘开裂的热固耦合仿真计算研究
许晓娇,刘晓帆,杨 肖
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
制动盘开裂的热固耦合仿真计算研究
许晓娇,刘晓帆,杨 肖
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
径向热机疲劳开裂是车辆制动盘失效的主要原因之一,通过研究制动盘的温度场和应力场可以有效揭示制动盘热机疲劳裂纹开裂机理.借助有限元分析软件ANSYS,研究车辆在初始制动速度分别为60 km/h,120 km/h和180 km/h工况下制动盘的温度场和等效应力场.仿真结果表明,在3种工况下,制动盘表面最大温度分别为129 ℃,241 ℃和357 ℃,最大等效应力分别为122.00 MPa,245.00 MPa和326.00 MPa.同时对比制动盘周向热应力和径向热应力,发现在3种工况下的周向热应力均大于径向热压应力.当初始制动速度在180 km/h以上时,周向残余拉应力开始大于径向残余拉应力,导致制动盘表面产生径向断裂裂纹,造成制动盘失效.该模拟研究为今后抗疲劳制动盘优化设计和试验研究提供了重要参考依据.
有限元计算;制动盘;周向残余拉应力;径向裂纹
0 引 言
盘式制动器因其构造简单、重量轻、散热快和调整方便等诸多优点被普遍用于各类车型中,制动盘是盘式制动器的核心零部件之一,是保证车辆安全运行的关键组成[1-2].随着车辆设计运行速度不断提高,热机疲劳开裂已成为制动盘失效的主要原因,给车辆安全运行带来隐患.研究制动盘温度场和应力场,对揭示制动盘热机疲劳开裂机理以及设计新型高效抗疲劳制动盘具有重要研究价值.目前,针对制动盘的研究方法主要有试验法和有限元分析法.试验法包含1:1台架试验和等比例缩减试验的各类检测试验[3-5].与有限元计算法相比,试验法获得的结果相对准确可靠,但需要周期较长、试验载荷条件难以施加.因此,大量学者采用有限元计算方法研究制动方式、制动工况等对制动盘瞬态温度场的影响[6,7].也有许多学者运用有限元软件MSC.Patran和MSC.MARC建立了二维轴对称模型,计算制动盘在不同制动压力下的温度场与应力场[8-10].钱立军等[11]建立了三维循环对称制动盘模型,运用ANSYS计算制动盘及相关部件在初始制动速度为200 km/h工况下的三维瞬态温度场,发现制动盘摩擦表面的最大温度可达到220 ℃.然而上述学者未针对制动盘热机疲劳开裂的形式及原因给出解释.
本文通过有限元计算法,综合考虑了有限元网格敏感性及制动盘材料属性的变化规律,对初始速度为60 km/h,120 km/h和180 km/h工况下的制动盘进行模拟,研究其温度场和应力场,分析导致制动盘产生周向和径向裂纹规律及原因.
1 有限元建模与边界载荷计算
1.1 制动盘实体模型
本文以典型商用车辆制动盘为研究对象,制动盘外径R1=128.00 mm,制动盘内径R2=32.50 mm,制动盘摩擦面厚度H1=12.50 mm,摩擦片覆盖角θ=64.5°,摩擦片外径R3=125.00 mm,摩擦片内径R4=77.00 mm,摩擦片厚度H2=14.50 mm.由于制动盘具有中心轴对称结构特征,制动盘造型图如图1(a)所示.因此在建立常规制动盘热机耦合有限元模型时将其简化为二维剖面模型,制动盘轴对称截面图如图1(b)所示.
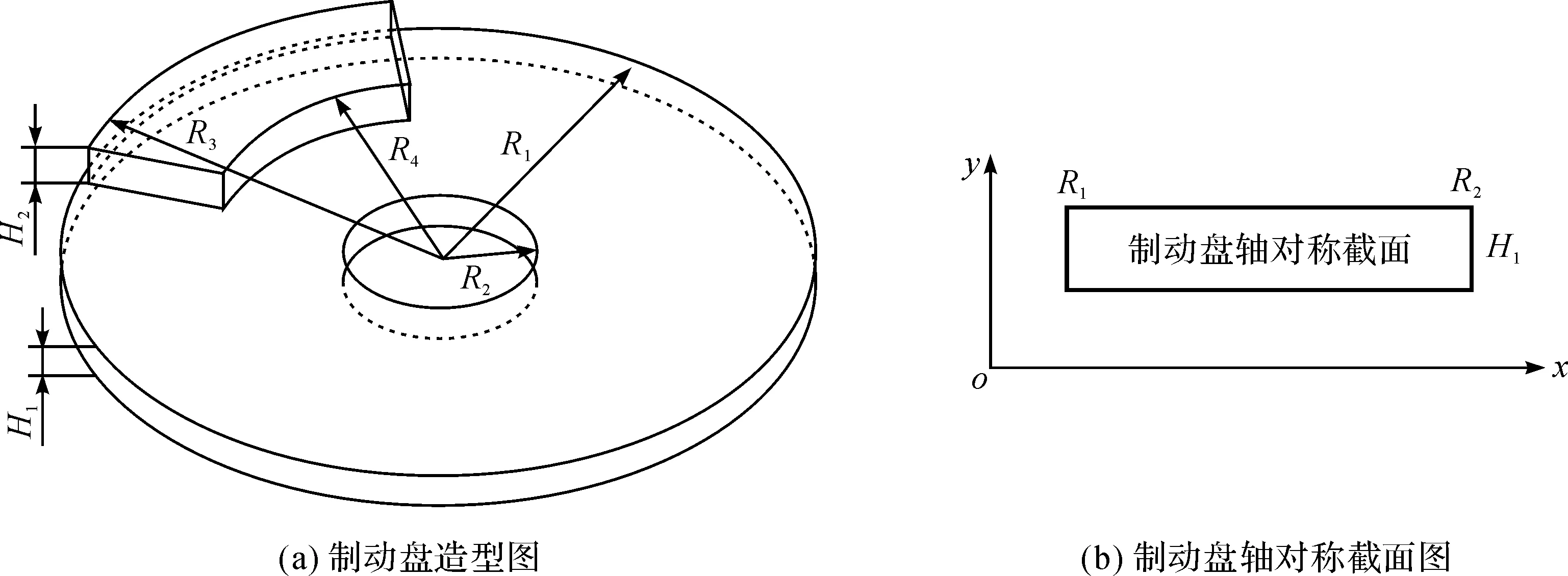
图1 制动盘实体模型示意图
1.2 制动盘材料属性及力学性能
制动盘材料为灰铸铁HT 200,其化学成分质量百分比为:w(C)=3.250%,w(Si)=1.570%,w(Mn)=0.920%,w(P)=0.060%,w(S)=0.059%,其余为Fe,物理属性随温度变化的参数如表1所示,弹性模量为101.027 GPa,泊松比为0.27.灰铸铁微观组织由珠光体和石墨组成,属于脆性材料,同时由于石墨的存在导致灰铸铁材料力学性能各向异性,因此,在仿真模拟计算中,准确选择材料力学模型和定义灰铸铁材料的拉/压应力—应变曲线可精确模拟灰铸铁热机耦合状态下应变应力场.

表1 制动盘基体材料随温度变化的相关物理参数
1.3 热力耦合模型边界载荷
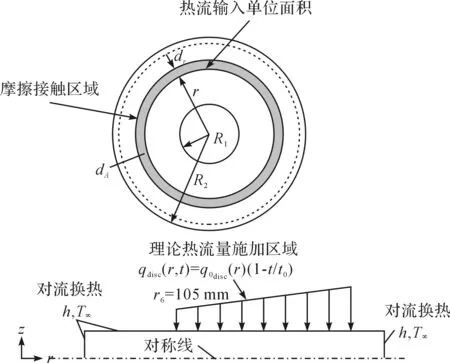
图2 热流密度边界载荷
在制动过程中95%的动能转换成热能被摩擦副吸收,而摩擦片多为非金属复合材料,热导率远低于制动盘热导率仅约为其2.5%,大部分热能被制动盘吸收,因此本文假设摩擦产生的热量全部被制动盘吸收,即热量分配系数σ=1.在理想状态下,摩擦片与制动盘间为面面接触,摩擦副产生的热流均匀流入制动盘环形摩擦接触区域,如图2所示.根据能量守恒原理,对初始动能求导后可获得热流量,热流量大小是与制动压力p=3.17 MPa、摩擦系数μ=0.45、制动时间t=3.41 s、制动盘摩擦接触半径r=48.00 mm以及初始制动速度v=60 km/h,120 km/h,180 km/h相关的函数,计算公式如下:
(1)
dSdisc=2πrdr
(2)

(3)
式中:Ff为摩擦力;r为制动盘半径;t为时间;E为吸收的总能量;p1为接触面压强;σ为摩擦片与制动盘间能量分配比,σ=1;μ为摩擦系数;ω为制动盘选择角速度;φ0为摩擦片与制动盘接触覆盖角.
3种工况下的热流密度分别为:车辆制动初始速度为60 km/h时,热流密度q60=2.555 812×105×(53.07-15.56×t)×r;车辆制动初始速度为120 km/h时,热流密度q120=2.555 812×105×(106.152-31.12×t)×r;车辆制动初始速度为180 km/h时,热流密度q180=2.555 812×105×(159.288-46.96×t)×r,单位为w/m2.
1.4 制动盘有限元网格模型
为验证有限元网格的稳定性,保证计算结果的准确性,本文给出3种尺寸下的网格状态,并提取相同位置的节点温度作为衡量指标进行验证.不同网格密度下的部分制动盘二维网格如图3所示,分别给出了3种制动盘的网格.不同网格密度下的温度结果如图4所示,可以看出不同网格状态下的温度结果几乎一致,可见有限元计算结果对网格的敏感性较弱,能够满足计算需求.因此,在以下模拟满足热机耦合计算需求前提下,本文选用第2种有限元网格.
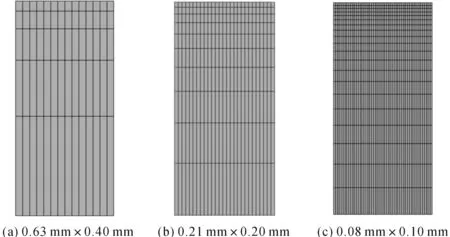
图3 制动盘二维网格
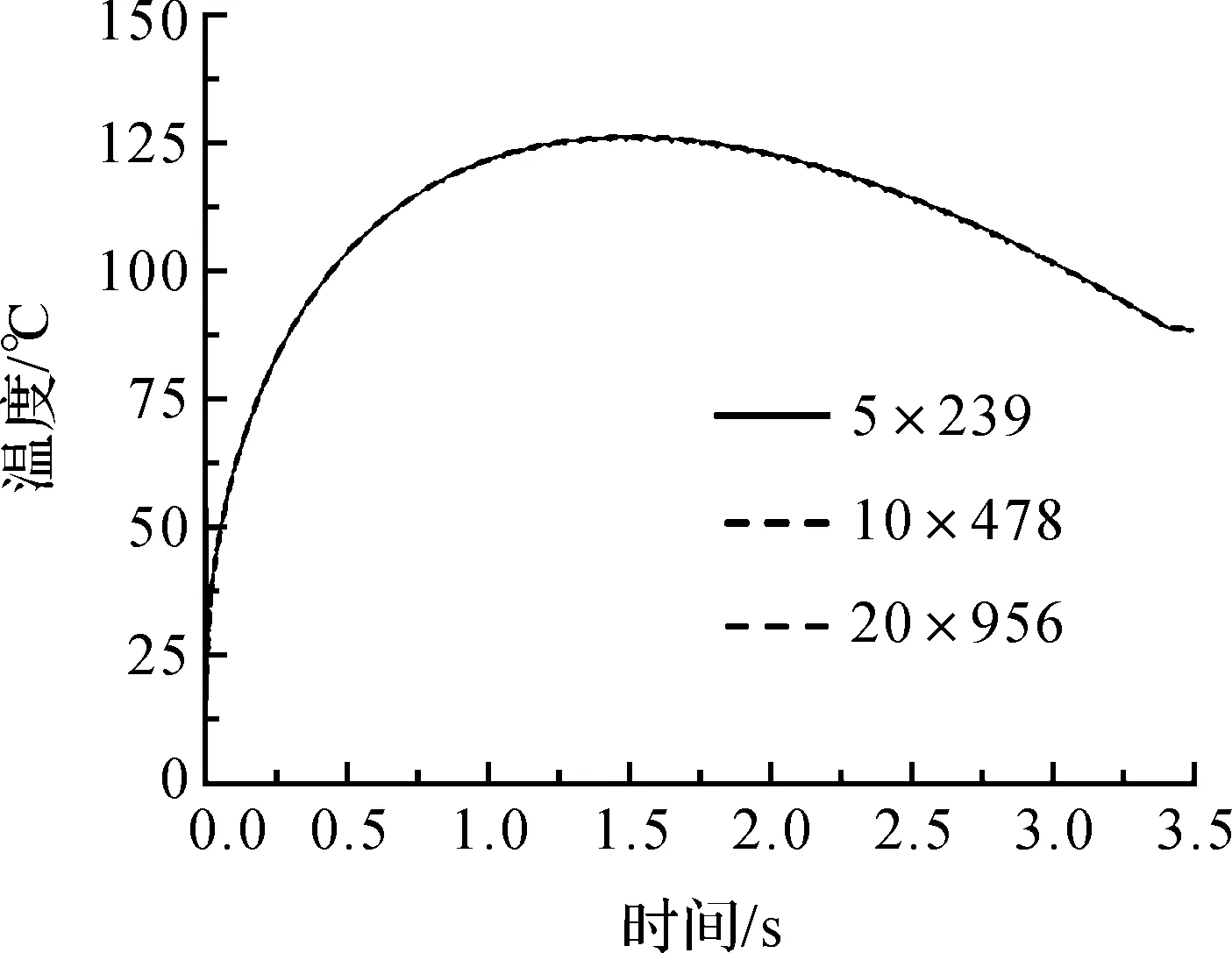
图4 不同网格密度下的温度结果
2 结果与讨论
2.1 制动盘温度场计算结果与分析
通过模拟获得了制动盘在不同工况的温度场、径向应力场、周向应力场及出现最大温度部位的应力随时间变化曲线,如图5所示.图5(a)为制动盘表面出现最大温度位置处的温度随时间变化曲线,当时间为t=1.70 s左右时,制动温度达到最大值,约为129 ℃,241 ℃和357 ℃.随后,由于制动盘的热传导和对流换热作用,流入制动盘表面的热量逐渐减小,温度开始下降.当时间为3.41 s时,制动停止,流入制动盘的热流停止,制动盘开始冷却.图5(b)展示了3种工况下整个模拟过程中的温度变化趋势,当时间t=1 200.00 s时,3种工况下,制动盘最终的冷却温度分别为30 ℃,45 ℃和60 ℃.
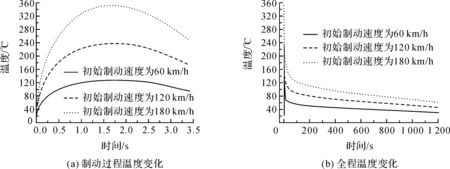
图5 制动盘最大温度随时间变化曲线
车辆初速制动度为60 km/h时,不同时刻的温度场分布如图6所示.由制动盘在t=1.70 s时的温度场可知,出现最大温度位置接近摩擦片外径边缘,并且高温区域的深度较小且集中在表面附近.在厚度方向上存在较大温度梯度,最大温差约为110 ℃;在径向上,存在的温度梯度与厚度方向基本一致.当制动结束时(t=3.41 s),在厚度方向上,由于热量向制动盘内部的传导作用,温度梯度逐渐减小,表面最高温下降至95 ℃,最大温差约为50 ℃.径向方向温度梯度约为75 ℃.经过20 min冷却后,制动盘在厚度和径向上几乎无温度梯度存在,整个盘体温度约为30 ℃.

图6 初速度为60 km/h时,不同时刻的温度场分布
初速制动度为120 km/h和180 km/h时,不同时刻的温度场分布如图7和图8所示.与初始制动速度为60 km/h的分布规律相似.在t=1.70 s时,制动盘径向和厚度方向的温度梯相近,分别约为222 ℃和338 ℃.当制动结束时(t=3.41 s),在度方向上由于热量传导作用,表面最高温分别下降至172 ℃和249 ℃,温度梯度分别约为102 ℃ 和153 ℃,径向的温度梯度分别约为152 ℃和229 ℃.经冷却,制动盘摩擦接触区域以下的区域,几乎无温度梯度存在.

图8 初速度为180 km/h时,不同时刻的温度场分布
2.2 制动盘应力场计算结果与分析
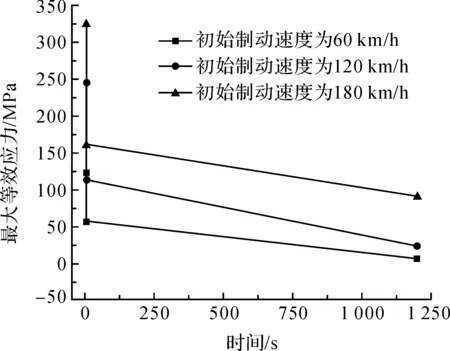
图9 3种工况下最大等效应力变化规律
在3种工况下,最大等效应力不同时刻的变化趋势如图9所示.初始制动速度为60 km/h时,最大等效应力分别为122.00 MPa,55.90 MPa和6.83 MPa;初始制动速度为120 km/h时,最大等效应力分别为245.00 MPa,113.00 MPa和22.40 MPa;初始制动速度为180 km/h时,最大等效应力分别为326.00 MPa,160.00 MPa和89.80 MPa.出现最大等效应力的位置位于摩擦片外径边缘处,在不同初始制动速度下,制动盘von mises应力分布如图10-12所示.该位置与制动盘表面出现最大温度的位置相同.究其原因,由于受到轴对称结构的约束,在制动盘内径处会产生结构约束反力,而在制动盘的外径处,由于没有结构的约束作用,外径处的等效应力要小于内径处应力.

图11 初始制动速度为120 km/h时,制动盘von mises应力分布云图

图12 初始制动速度为180 km/h时,制动盘von mises应力分布云图
图13-14分别给出了制动盘在3种工况下径向与周向最大应力的变化规律.由图14可知,在整个制动过程中,周向与径向应力在制动初期均为压缩应力.在制动结束后,压缩应力变为拉伸应力.图14中,制动前10.00 s,周向与径向应力在0.10 s之前大小几乎相同,随着时间增加,两者增长速率明显不同,周向应力开始大于径向应力.当t=1.00 s时,径向压缩应力达到最大值,而周向应力则在t=1.50 s时达到最大值.即制动盘在周向更容易发生塑性变形,产生热开裂.对比图14中的残余拉应力大小可知,初始制动速度提高,周向和径向残余拉伸应力增大,残余周向拉应力大于径向残余拉应力.
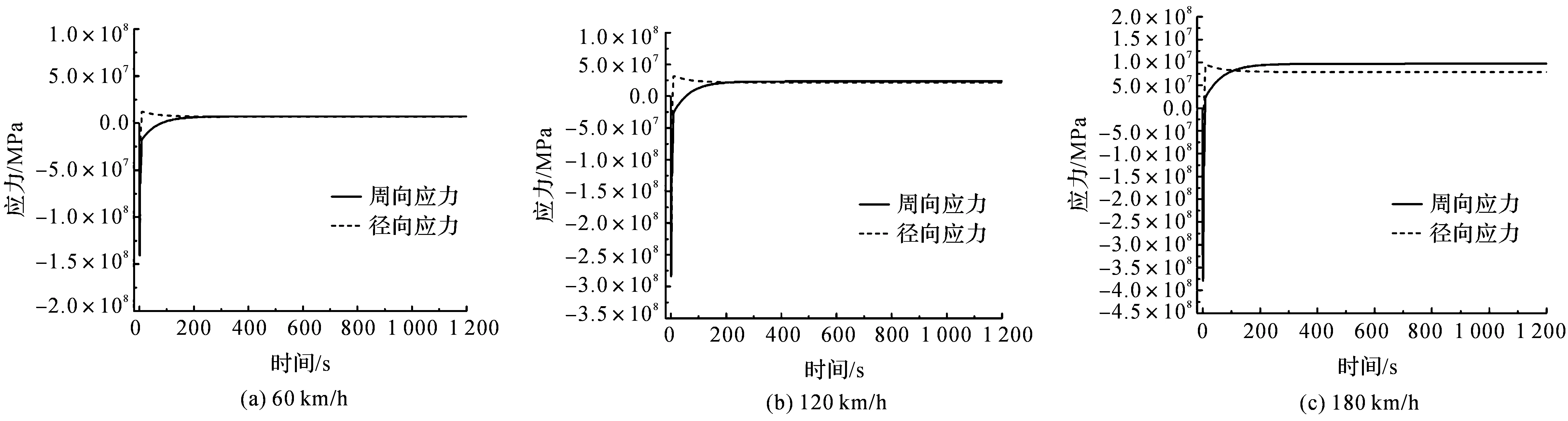
图13 不同初始制动速度下,径向和周向最大应力随时间变化趋势
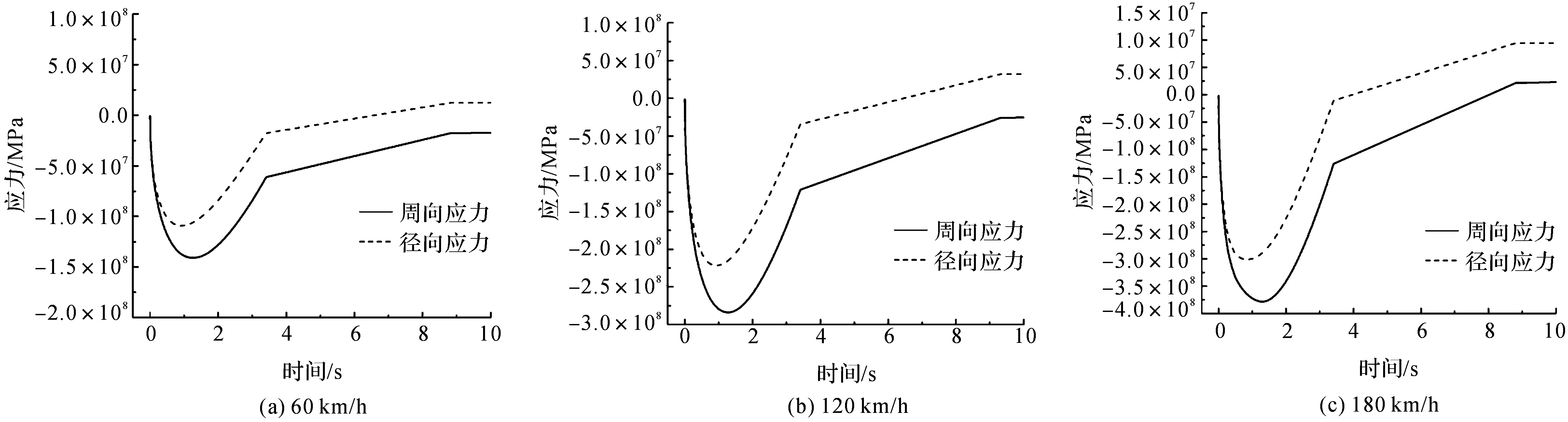
图14 不同初始制动速度下,径向和周向最大应力在制动初期随时间变化趋势
上述受力分析表明,制动盘表面更容易产生径向裂纹,并且裂纹的数量要多于周向裂纹,因此,在制动盘热疲劳性能提升设计中,首先应从加强制动盘的周向强度出发,提高制动盘抗周向变形以及抵抗周向残余拉伸应力,从而提高制动盘的抗变形和抗开裂性能.
3 结束语
本文针对现有车辆制动盘存在径向热机疲劳开裂的问题,通过研究制动盘的温度场和应力场有效揭示了制动盘热机疲劳裂纹开裂机理.仿真及分析结果表明,在3种工况下制动盘周向热应力均大于径向热压应力,当初始制动速度在180 km/h以上时,周向残余拉应力开始大于径向残余拉应力,导致制动盘表面产生径向断裂裂纹,造成制动盘失效.本文的研究为今后抗疲劳制动盘优化设计和试验研究打下了基础.
[1] 杨肖,张志辉,王金田,等.仿生制动盘表面温度场与应力场的计算机模拟[J].机械工程学报,2012,48(17):121-127.
[2] 杨肖.制动盘仿生耦合表面抗疲劳性能研究[D].吉林:吉林大学,2015.
[3] VALLET F. Etude de la fissuration d’un disque de frein a partir de l’analyse de son comportement thermomécanique[D]. Lille:Lille Ecole de Central de Lille, 1999.
[4] GOO B C, LIM C H. Thermal fatigue evaluation of cast iron discs for railway vehicles[J]. Procedia Engineering, 2010,2(1):679-685.
[5] SUKEDA A, MORI T, SUZUKI S, et al. Development of disc brake rotors for trucks with high thermal fatigue strength[J]. Jsae Review, 2002,23(1):105-112.
[6] 张乐乐,杨强,谭南林,等.基于摩擦功率法的列车制动盘瞬态温度场分析[J].中国铁道科学,2010,31(1):99-104.
[7] 应之丁,李小宁,林建平,等.列车车轮踏面制动温度循环试验与温度场仿真分析[J].中国铁道科学,2010,1(3):70-75.
[8] 赵海燕,张海泉,汤晓华,等.快速列车盘型制动热过程有限元分析[J].清华大学学报(自然科学版),2005,45(5):589-592.
[9] 林谢昭,高诚辉.紧急制动过程制动盘表面非轴对称温度场的数值模拟[J].摩擦学学报,2002,22(s2):366-369.
[10] 黄健萌,高诚辉,唐旭晟,等.盘式制动器热—结构耦合的数值建模与分析[J].机械工程学报,2008,44(2):145-151.
[11] 钱立军,余武弦,杨年炯.盘式制动器摩擦片瞬态温度场分析[J].客车技术,2008(6):22-25.
TheSimulationStudyofBrakeDisconCrackedThermo-solidCoupling
XU Xiaojiao, LIU Xiaofan, YANG Xiao
(SchoolofMechanicalEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
The radial fatigue crack is the primary reason of the brake disc failed of vehicles. The study on thermal and stress field of brake disc can reveal the mechanism of radial fatigue crack of heat engine. Based on finite element ANSYS software, study on thermal and stress field of brake disc done at the situation when the initial velocity of vehicle is 60 km/h, 120 km/h, 180 km/h, and result of simulation indicate that the maximum temperature of surface reach up to 129 ℃, 241 ℃, 357 ℃ respectively, and the maximum residual tensile stress is 122.00 MPa, 245.00 MPa, 326.00 MPa, respectively. Compared tangential thermal stress with radial thermal stress, and the former is higher at any time. When the initial velocity of vehicle is 180 km/h, the tangential residual tensile stress is higher than radial one, lead to radial crack on surface of brake disc, which makes the brake disc come to fail. This simulation research provides primary reference on optimization design and experimental study of anti-fatigue brake disc.
finite element calculation; brake disc; tangential residual stress; radial crack
TB24
A
1001-9146(2017)05-0072-06
2016-12-26
浙江省公益技术应用研究资助项目(2016C31046)
许晓娇(1992-),女,浙江台州人,硕士研究生,制动盘摩擦性能研究.通信作者:杨肖讲师,E-mail:yangxiao@hdu.edu.cn.
10.13954/j.cnki.hdu.2017.05.014

