二部图中的完美匹配子集权的极小化问题
李伟娟,陈光亭,陈 永,张 安
(杭州电子科技大学理学院,浙江 杭州 310018)
二部图中的完美匹配子集权的极小化问题
李伟娟,陈光亭,陈 永,张 安
(杭州电子科技大学理学院,浙江 杭州 310018)
主要研究了二部图中的完美匹配子集权的极小化问题,针对完美匹配两个子集权的极小化问题,证明了最小权重优先算法SWF的最坏情况界为3/2,并应用一一互换思想,设计了最坏情况界至多为4/3的改进算法.
二部图;完美匹配;近似算法;最坏情况界
0 引 言
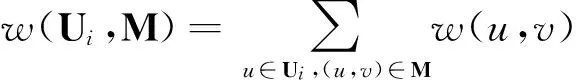
1 问题陈述及符号说明
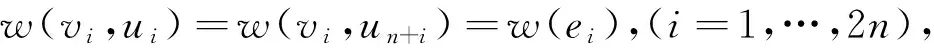
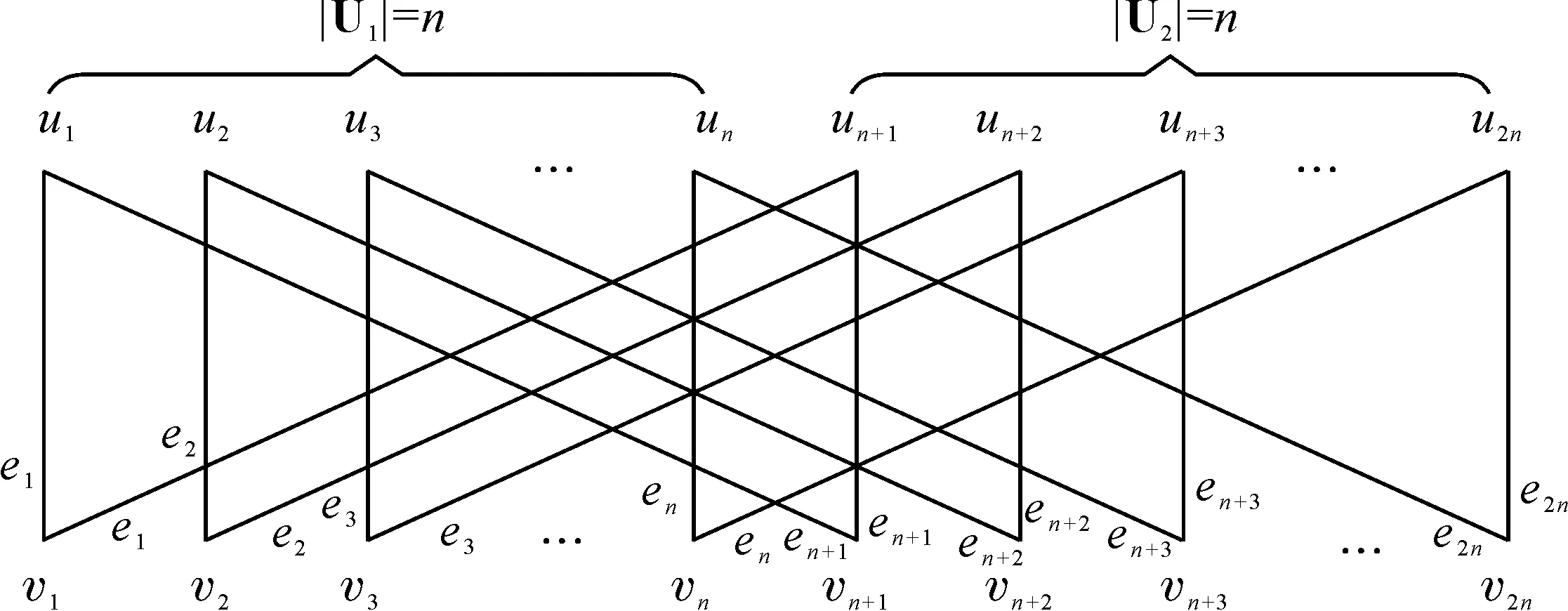
图1 问题示意图
2 近似算法及最坏情况分析
最小权重优先(Smallest Weight First, SWF)算法的基本步骤如下:
1)将权重按照从小到大的顺序排序w(e1)≤w(e2)≤…≤w(e2n);
2)从权重最小的边开始,依次放入当前边权和最小的子集U1或者U2里.
引理按照SWF算法,最终得到2个集合U1和U2里边的条数一定相等.
证明反证法.若集合U1和U2里边的个数不相等,一定存在一条边em,不妨设em在U2,在em放入U2之前,记w(U2)=sm,w(U1)=r分别表示子集U2,U1的权重,则有
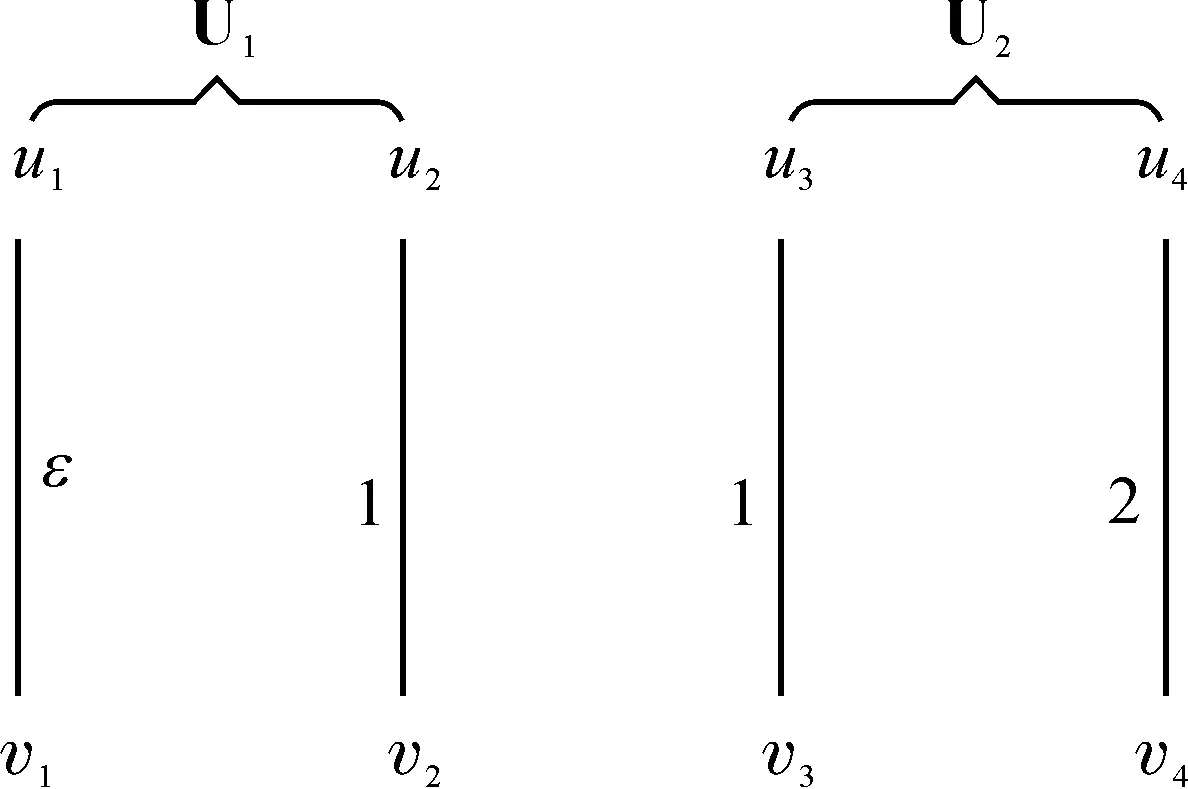
sm+w(em) (1) 定理1SWF算法的最坏情况界不超过3/2且是紧的. 证明记M1为SWF算法得到的完美匹配,设边权w(e2n)放入子集U2时,U2中的边权和记为s2n,则有 实例说明3/2的界是紧的.Ui=2(i=1,2),U1有2个点u1,u2.U2有2个点u3,u4.V=4,V中有4个点v1,v2,v3,v4.各边的权重分别为: w(e1)=w(v1,u1)=w(v1,u3)=ε,w(e2)=w(v2,u2)=w(v2,u4)=1,w(e3)=w(v3,u3)=w(v3,u1)=1,w(e4)=w(v4,u4)=w(v4,u2)=2. 图2 最优解 图3 算法解 下面给出改进的一一互换算法.令U1,U2是e1,e2,…,e2n的一个划分且Ui=n(i=1,2),不妨假设w(Uq) 互换算法的步骤如下: 1)将U任意划分成边数相等的两个子集Ui(i=1,2); 2)不断进行上述的一一互换过程,直至不能进行互换为止. 定理2互换算法的最坏情况界至多是4/3. 证明记M2为互换算法得到的完美匹配,假定w(M*)=1(w(ei)除以w(M*)).因此对于划分U1,U2有 (2) 假设w(U1)=1+α且w(U1)是子集中权和最大者,w(U2)是子集中权和较小者.记Δ12=w(U1)-w(U2),δ12=minw(er)-w(es)|w(er)-w(es)>0,er∈U1,es∈U2若U1,U2已不能进行一一互换了,那么Δ12≤δ12,根据式(2)可得 Δ12=w(U1)-w(U2)=2w(U1)-(w(U1)+w(U2))≥2(1+α)-2=2α. 本文主要研究了二部图中的完美匹配子集权的极小化问题,首先设计了最小权重优先算法并证明了算法的最坏情况界为3/2且是紧的.其次,根据一一互换思想,设计的改进算法的最坏情况界至多为4/3.下一步将对集合U的个数m>2的情况做进一步研究. [1] BARKETAU M, PESCH E, SHAFRANSKY Y. Minimizing maximum weight of subsets of a maximum matching in a bipartite graph[J]. Discrete Applied Mathematics, 2015,196:4-19. [2] BOYSEN N, FLIEDNER M. Determining crane areas in intermodal transshipment yards: The yard partition problem[J]. European Journal of Operational Research, 2010,204(2):336-342. [3] BOYSEN N, FLIEDNER M, JAEHN F, et al. A survey on container processing in railway yards[J]. Transportation Science, 2013,47(3):312-329. [4] BURKARD R E, DELL’AMICO M, MARTELLO S. Assignment Problems, Revised Reprint[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2009:383-386. [5] PAPADIMITRIOU C H, STEIGLITZ K. Combinatorial optimization: algorithms and complexity[M]. Englewood:Prentice-Hall, 1982:495-496. [6] CARPANETO G, TOTH P. Algorithm for the solution of the bottleneck assignment problem[J]. Computing, 1981,27(2):179-187. [7] FUJITO T, NAGAMOCHI H. A 2-approximation algorithm for the minimum weight edge dominating set problem[J]. Discrete Applied Mathematics, 2002,118(3):199-207. MinimizingMaximumWeightofSubsetsofaPerfectMatchinginaBipartiteGraph LI Weijuan, CHEN Guangting, CHEN Yong, ZHANG An (SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China) This paper studies the minimization problem of perfect matching subset weights in bipartite graphs. It first proves that the worst case ratio of the SWF algorithm is 3/2, and then an improved algorithm using the one to one exchange idea is presented, which is shown to be 4/3-approximation. bipartite graph; perfect matching; approximation algorithm; worst-case ratio O221.7 A 1001-9146(2017)05-0097-03 2016-12-05 国家自然科学基金资助项目(11571252,11401149);浙江省自然科学基金资助项目(LY16A010015) 李伟娟(1989-),女,河南荥阳市人,硕士研究生,组合优化.通信作者:陈光亭教授,E-mail:gtchen@hdu.edu.cn. 10.13954/j.cnki.hdu.2017.05.018
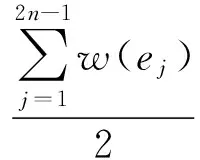
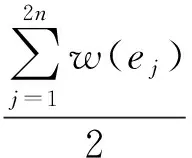
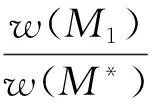

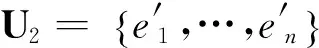
3 结束语

