基于改进型Henon映射的图像加密算法
蒋诗意,王光义,靳培培
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
基于改进型Henon映射的图像加密算法
蒋诗意,王光义,靳培培
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
在传统的Henon二维映射基础上,提出了一种改进型的Henon映射,增加了其序列复杂性和密钥空间.NIST测试表明,改进后的混沌序列具有良好的随机性.为了提高图像加密的安全性,利用此混沌序列设计了一种新的图像加密算法,将产生的两个混沌序列融合在一起组成了一个新的随机序列作为密钥序列.通过仿真验证了算法良好的加解密效果,降低了图像相邻像素间的相关性.解密时,改变其初始密钥后,无法正确解密,表明该算法具有良好的密钥敏感性,而计算所得的密钥空间非常大,表明该算法能有效地抵抗唯密文攻击,因此具有较高的安全性.
Henon映射;改进;图像加密;混沌
0 引 言
随着网络技术的不断发展,信息数字化的趋势越来越明显,人们对信息安全也越来越重视,但是常见的传统加密算法安全性低,效率低,易破解,已无法满足信息安全日益增长的需求.加密算法应满足安全性高、抗破解能力强等要求,混沌系统具有良好的伪随机性以及对初始条件的敏感性等特点,能很好地解决传统加密算法中的缺点[1-5].目前,将混沌序列作为加密密钥对图像信息进行加密,已成为国内外的研究热点.
近年来,在Chen G.R.等[6]提出的典型“置乱—替代”结构的混沌加密算法的基础上,越来越多的人致力于研究更安全、更高效率的图像加密算法.简单的“置乱—替代”加密算法效率非常高,但是不能有效的抵抗明文的攻击,针对这一问题,大量的文献提出了改进的图像加密算法[7-9].文献[8]提出了一种基于选择明文和选择密文的图像加密算法,通过选择特殊的密文策略,使新增的密文反馈机制失效,从而增加了算法的安全性,但该算法的效率不高.文献[10]根据Henon映射设计了一种改进的图像加密算法,对图像像素点的灰度值计算从原来的单点循环迭代改进为双点迭代循环,提高了算法的加密效率.然而传统的Henon映射混沌参数区间小,导致加密算法的密钥空间小,为此,本文提出了一种改进型的Henon映射,并根据此映射设计了一种的新的图像加密算法,增大了密钥参数的空间和序列的伪随机性,提高了图像的安全性.
1 改进型Henon映射
1.1 Henon映射的改进
传统Henon映射的系统方程为:
(1)
当b=0.3,a∈[1.1,1.4]时,系统处于混沌状态,传统Henon映射系统结构简单,但是产生混沌的参数区间小.本文经过多次对其分岔图的理论分析实验以及NIST测试发现,在原有方程的基础上增加余弦项,能够很好地扩大其参数范围,并且结构也比较简单,改进后的系统方程为:
(2)
当b=0.3,a=3.3时,系统处于混沌状态.图1(a)为传统的Henon映射状态变量x随着参数a变化的分岔图,图1(b)为吸引子图.图2(a)、(b)分别为改进后的分岔图和吸引子图.对比图1和图2可以看出,改进后的Henon映射出现混沌的参数范围明显增大,当b=0.3,a∈[1.8,2.0]∪[2.4,2.7]∪[3.0,3.6]时,系统处于混沌状态;且x与y的迭代范围也有所增加,因此,密钥空间增大.根据Jacobi方法计算可得,传统的Henon映射Lyapunov指数为L1=0.634 8,L2=-1.838 8,改进后的为L1=1.172 0,L2=-3.061 6,改进系统的Lyapunov指数明显提高.
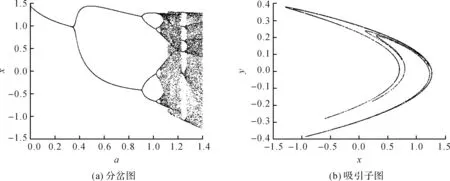
图1 传统Henon映射的分岔图和吸引子图

图2 改进型Henon映射的分岔图和吸引子图
1.2 混沌序列的NIST测试
为了进一步了解改进型Henon映射所产生的混沌序列的随机特性,利用美国国家技术标准局NIST推出的软件包STS对映射的序列进行了随机性测试,测试结果如表1所示.
NIST提供了两种评判序列性能的依据,一是序列的通过率必须大于0.980 560 7;二是P-value值需均匀性分布,即当P-value的值大于等于0.000 1时,测试序列的分布式均匀的.从表1中可以看出,改进型Henon映射所产生的混沌序列具有良好的随机性,15项性能测试指标全部通过,并且是均匀分布的,部分测试指标优于传统Henon映射.因此,改进后的Henon映射具有良好的随机性,适合作为密钥序列应用于信息加密中.
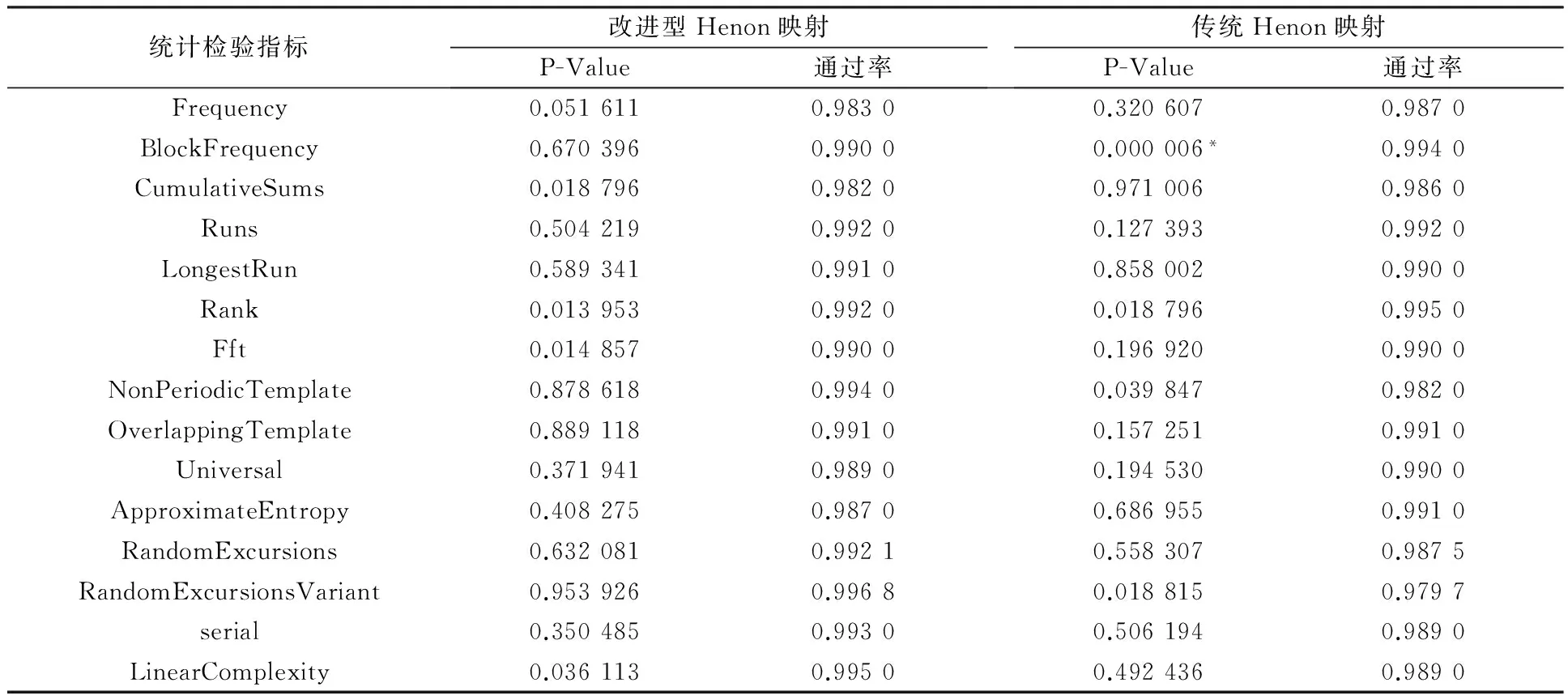
表1 改进型Henon映射与传统Henon映射的NIST测试结果
2 图像加密算法设计
数字图像可以看成是由一个个像素点M×N组成的二维矩阵,本文采用改进后的Henon映射产生的混沌序列作为密钥序列对图像进行加解密.加解密流程如图3所示.
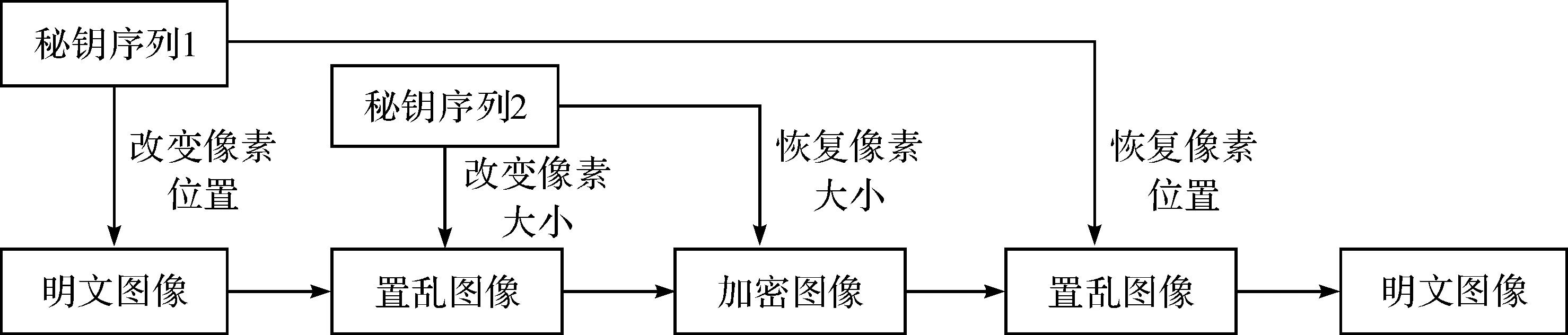
图3 加解密流程图
本文设计的图像加密算法步骤如下:
1)产生密钥序列.
将x,y的初始值代入式(2),循环迭代M×N次后,产生混沌序列{x(i)}和{y(i)},为了增加密钥的随机性,将{x(i)}和{y(i)}融合在一起作为密钥序列:分别取{x(i)},{y(i)}的第i个到第(i+k)个数据,把这2k个数据组合在一起成为一个新的序列{z(j)},取{x(i)},{y(i)}的第(i+k+1)个到第(i+2k)个数据,将这2k个数据按顺序添加序列{z(j)}中,重复上述方法,直到序列{z(j)}的长度为M×N,如图4所示.
图4 密钥序列的产生过程
2)置乱图像.
将步骤1中生成的密钥序列进行从小到大的排序,得到一个表示排序后的元素在密钥序列中的位置信息的序列,将其转化为M×N的二维矩阵并作为置乱矩阵E(M×N),明文图像G(M×N)像素位置按照置乱矩阵变化,即可得到置乱后的图像G′(M×N).
3)改变图像像素值大小.
交换x,y的初始值,重新迭代产生混沌序列后,重复步骤1中的融合方法,生成用于改变图像像素值大小的密钥序列{w(j)},并将其转换成二维矩阵W(M×N),由于图像像素值大小G′(i,j)∈[0,255],所以需要将W(M×N)的值转换成[0,255]之间,公式转换如下:
W′(i,j)=floor(1 000|W(i,j)|)mod 256
(3)
最后,将W′(M×N)与置乱图像G′(M×N)对应元素进行异或运算:
G″(i,j)=W′(i,j)⊕G′(i,j)
(4)
即可得到二次加密后的最终密文图像.
3 实验结果
按照上述算法流程,利用Matlab对经典的Lena图像进行加密,选择参数a=3.3,b=0.3,x,y的初始值分别取0.1,0.2,k=10,实验结果如图5和图6所示.

图5 加密结果
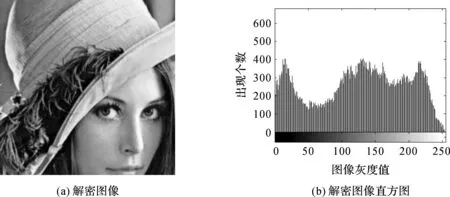
图6 解密结果
从实验结果可知,一次置乱后的图像已无法看清原始图像信息,但是直方图并没有改变,而经过二次异或加密后的图像已经无法辨识,且直方图分布均匀,没有明显的统计特征.解密时保持所有参数不变,对图5(c)进行解密,解密后的图像与直方图如图6所示,基本与明文图像一致,由此可知,改进算法具有良好的加解密效果.
明文图像相邻像素间具有较强的相关性,为了验证本加密算法能够很好地消弱图像相邻像素间的相关性,分别从明文图像、置乱后的图像以及加密图像中选取1 000对相邻像素,并且分别从它们的水平、垂直、对角线方向对其相关性进行分析,各图像相邻像素间的相关系数如表2所示.

表2 各图像相邻像素间的相关系数
从表2可以看出,加密后的图像明显削弱了相邻像素间的相关性,很好地掩盖了明文图像的信息.
水平方向明文图像和加密图像的相关性散点如图7所示.从图7可以更加直观地看到明文图像相关性比较高,而加密后的图像其相邻像素间的相关性很低.

图7 图像相邻像素间的相关性散点图
4 安全性分析
为了检验算法的安全性,改变x,y的初始值,将x=0.1改为x=0.100 001,其余参数与初始值不变,解密得到的图像与直方图如图8所示.从图8可以看出,当密钥参数和初始值发生微小改变时,采用相同的解密方法,仍旧无法正确解密.为了进一步说明本文提出的加密算法的密钥敏感性,将传统Henon映射的初始值x进行同样微小的改变后,对加密图像进行解密,其效果如图8(c)所示,从图8(c)上可以明显看到,即使使用错误密钥也能正确解密,得到与明文图像信息一致的解密错误图像.对比图8(a)和图8(c)可以发现,本文提出的加密算法具有很好的密钥敏感性,只有正确的密钥参数才能正确解密.
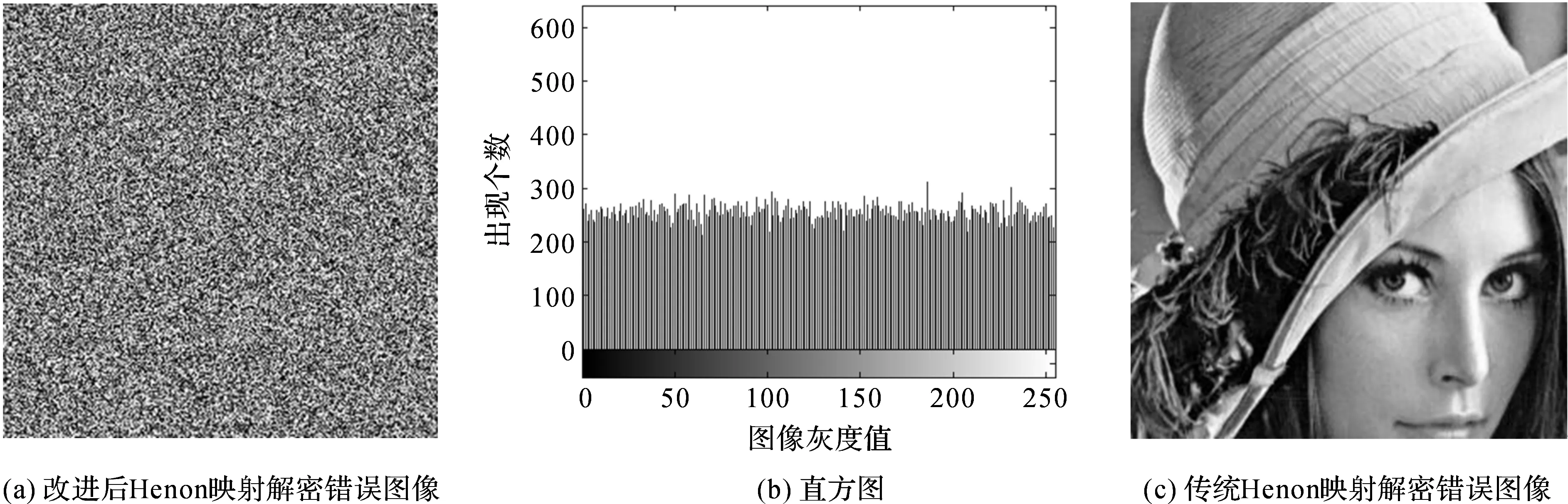
图8 密钥敏感性分析
改进后的Henon映射本身就增大了密钥空间,而本文所设计的图像加密算法中又引入了变量k,一般常用的计算机精度为10-16,因此本文所提出的算法的密钥空间至少为1080,能够很好地抵抗唯密文攻击.
5 结束语
本文首先对传统的Henon映射进行了改进,通过分析对比发现,改进后映射的参数区间以及x,y的迭代区间都有所增加,大大增加了其密钥空间.且经过分析表明,本文提出的改进型Henon映射能够产生随机性能良好的混沌序列.最后将改进的Henon映射应用于图像加密,提出了一个新的加密算法,在密钥空间和密钥敏感度方面都具有良好的效果,提高了图像的安全性.综合上述分析表明,基于改进型Henon映射的混沌图像加密算法具有广泛的应用前景,未来将探索更高效、更安全的图像加密算法.
[1] DENG S, ZHAN Y, XIAO D, et al. Analysis and improvement of a hash-based image encryption algorithm[J]. Communications in Nonlinear Science & Numerical Simulation, 2011,16(8):3269-3278.
[2] ZHANG Y Q, WANG X Y. A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice[J]. Information Sciences, 2014,273(8):329-351.
[3] 翟依依,王光义.基于Tent混沌序列的数字图像加密方法[J].现代电子技术,2014,37(12):73-77.
[4] 彭再平,王春华,林愿,等.一种新型的四维多翼超混沌吸引子及其在图像加密中的研究[J].物理学报,2014(24):97-106.
[5] ASKAR S S, KARAWIA A A, ALSHAMRANI A. Image Encryption Algorithm Based on Chaotic Economic Model[J]. Mathematical Problems in Engineering, 2014,2015:1-10.
[6] CHEN G R, MAO Y, CHUI C K, et al. A symmetric image encryption scheme based on 3D chaotic cat maps[J]. Chaos Solitons & Fractals, 2004,21(3):749-761.
[7] ZHANG Y Q, WANG X Y. Analysis and improvement of a chaos-based symmetric image encryption scheme using a bit-level permutation[J]. Nonlinear Dynamics, 2014,77(3):687-698.
[8] ZHU C, LIAO C, DENG X. Breaking and improving an image encryption scheme based on total shuffling scheme[J]. Nonlinear Dynamics, 2013,71(1/2):25-34.
[9] 廖雪峰.一种混沌双变换图像加密算法的分析与改进[J].温州大学学报:自然科学版,2014,35(1):8-16.
[10] 平萍,王志坚,许峰,等.一种基于Henon映射的图像加密算法的分析及改进[J].南京理工大学学报(自然科学版),2012,36(4):587-592.
ANewImageEncryptionAlgorithmBasedonImprovedHenonMapping
JIANG Shiyi, WANG Guangyi, JIN Peipei
(SchoolofElectronicInformation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Based on the traditional Henon two-dimensional mapping, an improved Henon mapping is proposed, which increases the complexity and the key space of the sequence. The NIST tests show that the improved chaotic sequences have good randomness. Then in order to improve the security of image encryption, a new image encryption algorithm is designed by using this chaotic sequence. And the algorithm fuses the two chaotic sequences to form a new random sequence as the key sequence. The simulation results show that the encryption and decryption effect of the algorithm is good and the correlation between adjacent pixels is reduced. It can’t be decrypted correctly after changing the initial encryption key which shows that the algorithm has a good key sensitivity. Then the large key space also shows that the algorithm can effectively resist cipher-text-only attack. So it has high security.
Henon map; improved; image encryption; chaotic
TN919.3
A
1001-9146(2017)05-0001-06
2016-11-09
国家自然科学基金资助项目(60971046,61281230357);浙江省自然科学基金重点资助项目(LZ12F01001)
蒋诗意(1991-),女,浙江海宁人,硕士研究生,非线性电路与智能信息处理.通信作者:王光义教授,E-mail:wanggyi@163.com.
10.13954/j.cnki.hdu.2017.05.001

