稀疏OFDM信道估计的同伦算法

钱 方，包建荣，许晓荣，姜 斌

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

稀疏OFDM信道估计的同伦算法

钱 方，包建荣，许晓荣，姜 斌

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

针对现有稀疏信道估计面临的复杂度过高、性能不佳、未充分利用稀疏性等缺陷，提出了联合压缩感知和同伦法的稀疏信道估计.主要通过跟踪正则因子，不断更新解方向和迭代步进，从而获得解的更新方程，具有复杂度低，性能好等优势.通过仿真及分析得到：在低信噪比条件下，与传统最小二乘法等算法比较，所提基于压缩感知同伦法的稀疏信道估计算法有20 dB性能增益，获得了较好估计性能.

稀疏信道估计；压缩感知；凸优化；同伦法

0 引 言

在无线通信系统中，信道估计是极为重要的研究方向.信号估计质量好坏将影响相干解调性能.与传统的奈奎斯特采样相比，压缩感知理论摒弃复杂的编码算法，同时进行数据的采集与压缩，其采样速率更低，重构信号更加精确[1].因无线多径信道多数都具有稀疏特性，且信道估计在很大程度上也属于信号重构问题，故应用压缩感知(Compressive Sensing,CS)理论.常用的信号重构算法主要有三种，一种是凸优化方法，凸优化是在凸函数限制的情况下，通过求解最小l1范数的凸优化问题恢复原始信号.凸优化方法主要包括基追踪(Basis Pursuit,BP)算法[2]、迭代收缩阈值(Iterative Shrinkage Thresholding,IST)算法[3]、梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction,GPSR)算法[4]以及同伦(Homotopy)法[5]等.文献[4]提出了一种常见的凸优化算法Barzilai-Borwein稀疏梯度投影法(GPSR-BB)以梯度下降法为基础，把一个隐变量代入目标函数中，将信号恢复问题转化为带有边界约束的二次方程优化问题，接着把算出的新目标方程的梯度值作为寻找最优值的方向.一种是贪婪追踪算法，它在搜索支撑集的过程中，利用了非零元素幅值的高低并求出它的具体值，之后再通过压缩测量值与估计出的稀疏解之间的残差来不断地更新支撑集.其中研究最多的两种方法是匹配追踪(Matching Pursuits,MP)算法以及正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[6].OMP算法是匹配追踪算法的一种改进.在每一次进行稀疏分解的同时，对选出的原子进行正则化处理，再更新原子集.另一种是贝叶斯法，利用贝叶斯理论中参数的先验分布和后验分布去研究信号恢复问题.贪婪追踪算法重建信号虽然速度很快，但是恢复精度却很低[7].而凸优化算法虽然重建信号的计算负担重，易受收敛停止准则影响，但是观测点数少，在局部求得的最优解就是整个区域上的最优值，同时当目标函数是严格的凸函数时，全局上只有一个最优值点[8].因此，本文将压缩感知中的Homotopy算法应用于OFDM信道估计中，将信道估计问题转化为压缩感知Homotopy算法中的信号重构问题.

1 CS理论及Homotopy算法

压缩感知CS指出，可以用一个与变换基不相关的观测矩阵来观测信号，将信号映射到一个低维空间上，这样重构问题就会转化为一个最优化问题，最后通过求解此优化方程就可将信号较为精确地重构出来.当然，如果想要进行以上的过程，信号需要满足一个前提条件，即信号在此变换域内可稀疏表示或者具有压缩性.压缩感知主要包括3个步骤：信号稀疏变换，观测矩阵设计及信号重构，其中信号重构步骤最为关键.

设信号为x：x∈RN，长度为N.在一般情况下，信号并非稀疏，但又具备可压缩性质.故为使信号可以被稀疏表示，可搜索一稀疏基Ψ，即有：

(1)

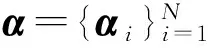
y=Φx=ΦΨα=Θα

(2)

其中，Θ=ΦΨ，Ф是观测矩阵.文献[9]指出：若要准确重构原信号，感知矩阵Θ需满足约束等距性质(Restricted Isometry Property, RIP)，即：

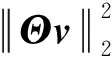
(3)

其中，δk是有限定距常数，且0<δk<1；v是任意矢量，具有k稀疏特性.

之后，重构信号.具体可将信号重构问题转化为最小化l1范数的最优化问题，如下：

(4)

因压缩感知理论具有精确恢复信号的特点.故其非常适合稀疏信道估计，不仅可极大减少导频数量，还可避免增加底噪.

同伦法以同伦思想为基础，根据前一次估值来估计信号的路径变化方向和步进，进而估计本次估计值.它主要针对小规模平稳信号，即幅值变化较小的目标信号.将同伦机制引入恢复算法中，可得动态更新最小化l1范数的恢复算法(DynamicX)[6].该算法利用前一次所估计出的数值来估计本次解的方向，同时也要制定相应的准则来不断的改变激活基的个数，符合停止准则的条件时即可结束.

设信号x缓慢变成了x′，则有：

y′=Φx′+n′

(5)

x′可通过下式得到：

(6)

引入同伦因子，则可得：

(7)

当正则因子ε逐渐由0增加到1，则可以得到最优解的条件为：

(8)

(9)

其中，Г是x*的支持集，z是支持集Г上x*的符号组成的|Г|维向量.

设第k次迭代时，可得解的移动方向为：

(10)

由式(10)可得最优解的变化趋势.为了能紧接临界同伦因子，还需引入一个迭代步进θ，且满足式(8)和式(9)，则有：

(11)

pk=ΦΤ[Φxk-y+εk(y-y′)]

(12)

dk=ΦΤ(Φ∂k+y-y′)

(13)

若要使得pk(j)+dkjΔε=±τ，需找到最小Δε，且有j∈Γc，则可得：

(14)

故其步进θ可计算为：

θ=min(θ+,θ-)

(15)

当求得路径方向∂x和步进θ后，就可以得到同伦因子和解更新方程，分别如下：

εk+1=εk+θ

(16)

xk+1=xk+∂x·θ

(17)

此外，支持集Г也需更新.而Dynamic X算法所选的同伦路径是正则因子的变化方向，正则因子的选取需要符合最优解的条件，即观测矩阵与残差相关度需不大于正则因子.由此可得：该算法不断变化同伦因子，跟踪正则因子，进而得到解的方向和迭代步进.

2 仿真结果

仿真参数如下：采用QPSK调制；信号长度N=32；非零抽头数K=6；信噪比的变化范围为0～30 dB；导频数目为62.

分别采用传统LS信道估计和CS信道估计进行仿真，仿真结果如图1所示.在同一信噪比SNR情况下，以OMP为代表的CS信道估计均方误差MSE低于传统最小二乘法LS信道估计均方误差，如当信噪比为5 dB时，LS的重构MSE为1.017 7，CS的MSE为0.012 8；同时，两种算法的MSE随着SNR的不断变大而减少，具有反比关系.在相同均方误差情况下，LS算法的SNR比CS算法多近20 dB.这正是因为采用压缩感知方法能更充分利用信道稀疏特性，利用较少的导频能有效恢复稀疏信道脉冲响应，极大提高信道估计性能.

分别对基于CS的Homotopy、OMP、BCS和GPSR-BB算法的重构MSE性能进行仿真.在信噪比为20 dB时，根据上述稀疏OFDM信道估计同伦算法原理仿真得到的结果如图2所示.由图2可知，当OMP算法收敛时，MSE在0 dB处波动；BCS的波动趋向比同伦法的波动趋向要衰减的更快，但其稳定度极差；GPSR-BB算法收敛MSE大于0 dB.基于GPSR-BB重构算法的重构均方误差能够快速收敛，但是重构均方误差的值却较高.因在同伦法中，拉格朗日因子τ用于残差和稀疏能力间的折衷，可以控制信号重建误差和稀疏能力间的平衡.因此可得以下结论：BCS算法优于同伦法，但却不稳定.GPSR-BB算法虽能快速收敛，但MSE较大.同伦法虽重构复杂度高于OMP算法，但重构性能优于OMP.

图1 传统LS信道估计方法与CS信道估计比较

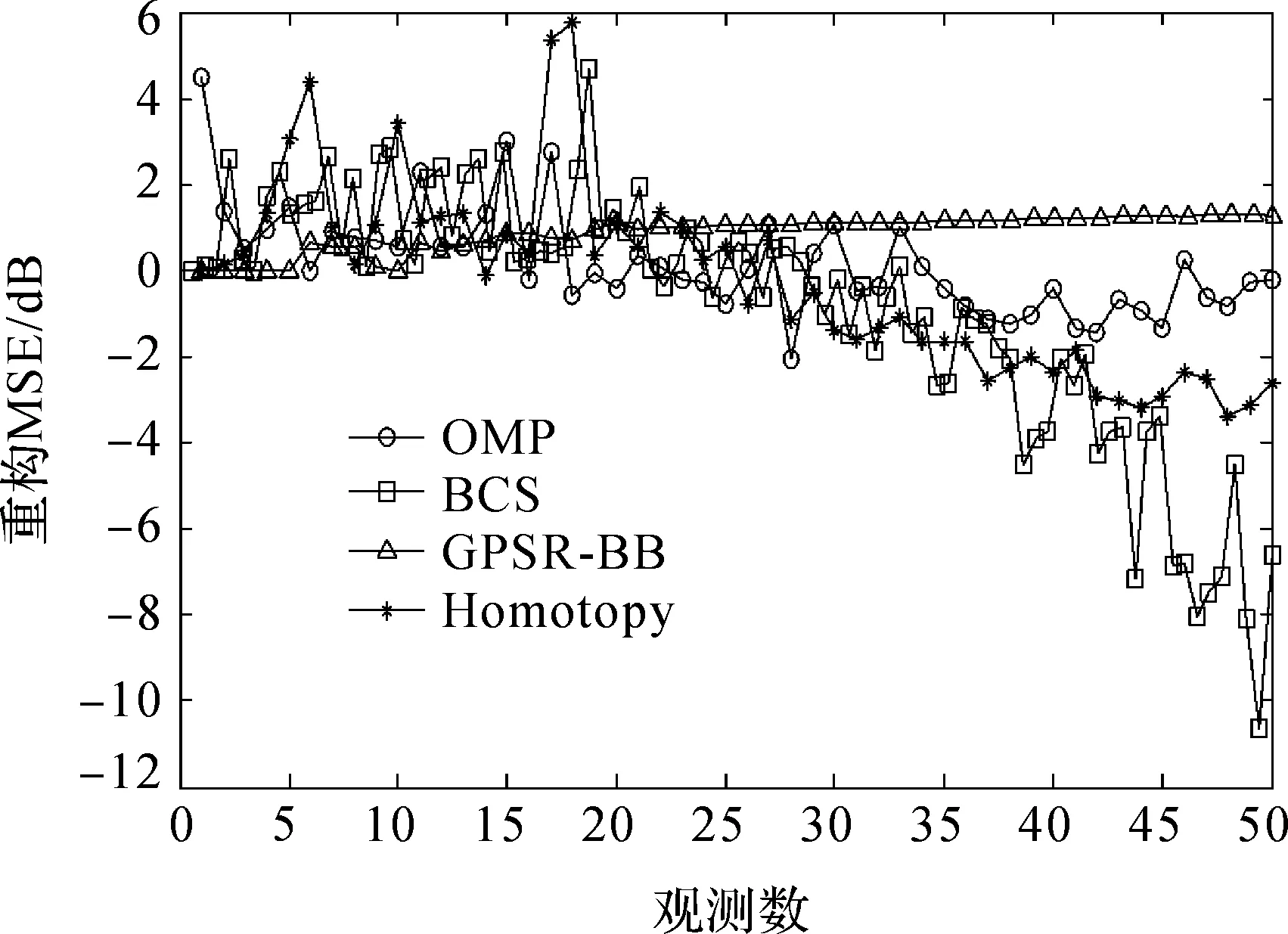
图2 4种算法的重构均方误差性能

对长度为256的OFDM信号采用不同迭代次数对信号重构性能的影响如图3所示.当迭代为1次时，τ=2.557 5，重构MSE为0.109 9；当迭代20为次时，τ=1.161 6，重构MSE为0.049 9；迭代为60次时，τ=0.431 5，重构MSE为0.019 6；当迭代次数为72次时，ε大于或等于1且此次估计值与前一次估计值差值要小于10-3，满足停止准则.所以当迭代次数为72时，重构MSE收敛，正则因子变为τ=5.420 9×10-13.因此，随着迭代次数不断增加，正则因子将不断减小并逐渐收敛，信号重构MSE下降，最终趋于收敛.在收敛时，正则因子为τ=5.420 9×10-13.

图3 BPDN-Homotopy正则因子与迭代次数关系图

3 结束语

本文提出了基于压缩感知同伦法的稀疏信道估计算法.与传统最小二乘法信道估计相比，精确度更高，估计性能得到了改善.同伦法采用迭代追踪同伦路径方法，不断更新了解方向，具有较高的重构精确度及较快的收敛速度；同时，增加迭代次数可减小信号重构均方误差.但复杂度较高，如何降低复杂度需进一步研究.

[1] QAISAR S, BILAL R M, IQBAL W, et al. Compressive sensing: From theory to applications, a survey[J].Journal of Communications & Networks, 2013,15(5):443-456.

[2] 焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1662.

[3] WRIGHT S J, NOWAK R D, FIGUEIREDO M A T. Sparse reconstruction by separable approximation[J]. Signal Processing, IEEE Transactions on, 2009,57(7):3373-3376.

[4] FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007,1(4):586-597.

[5] ASIF M S, ROMBERG J. Dynamic Updating for L1 Minimization[J]. IEEE Journal of Selected Topics in Signal Processing, 2010,4(2):421-434.

[6] TROPP J, GILBERT A C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit[J]. Information Theory, IEEE Transactions on, 2007,53(12):4655-4666.

[7] FOUCART S, RAUHUT H. A Mathematical Introduction to Compressive Sensing//[M]. Boston: Birkhöuser, 2013:44.

[8] 邓军.基于凸优化的压缩感知信号恢复算法研究[D].哈尔滨：哈尔滨工业大学,2011.

[9] SONG C B, XIA S T. Sparse Signal Recovery by Minimization Under Restricted Isometry Property[J]. IEEE Signal Processing Letters, 2014,21(9):1154-1158.

HomotopyAlgorithmforSparseOFDMChannelEstimation

QIAN Fang, BAO Jianrong, XU Xiaorong, JIANG Bin

(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Current sparse channel estimation is mainly confronted with the deficiencies, such as high complexity, poor performance, not adequately exploiting the sparse property, and so on. In order to solve these problems, a joint compressive sensing and the homotopy method is proposed to estimate the sparse channel. By tracking the change of regular factors, it constantly updates the direction of the solution and the iterative step. So it can obtain the solution of the update equation. It also has the advantage of low complexity, good performance and so on. The simulation channel estimation is better than the traditional least squares(LS) algorithm. At low signal-to-noise ratio(SNR), the proposed algorithm can obtain about 20 dB performance gain than that of the traditional algorithms. And the computational complexity is also reduced to 1/2 of that of the traditional algorithms. Therefore, it obtains a rather better estimation performance.

sparse channel estimation; compressive sensing; convex optimization; homotopy

TN911

A

1001-9146(2017)05-0017-04

2016-09-14

国家自然科学基金资助项目(61471152)；浙江省自然科学基金资助项目(LY15F010008,LZ14F010003)

钱方(1993-)，女，辽宁人，硕士研究生，现代稀疏信号处理.通信作者:包建荣副教授，E-mail:baojr@hdu.edu.cn.

10.13954/j.cnki.hdu.2017.05.004