中国老年人口死亡率的建模分析
黄佩佩,郑 静
(杭州电子科技大学理学院,浙江 杭州 310018)
中国老年人口死亡率的建模分析
黄佩佩,郑 静
(杭州电子科技大学理学院,浙江 杭州 310018)
基于1963—2014年60岁到110岁人口死亡率,采用k-means聚类方法,以余弦相似度为距离函数,将其聚为3类,针对每类采用时间序列分析的方法进行建模.每类中分别选取62岁,86岁和94岁的死亡率数据,利用1963—2006年数据进行建模,并用2007—2014年数据进行验证,其样本内拟合精度和检验样本预测精度都比较好,从而验证了所建模型的有效性和可行性.最后用该模型预测了2015—2020年62岁,86岁和94岁的人口死亡率.
死亡率;K-means聚类;ARIMA模型
0 引 言
人口死亡率一直是社会关注的一个焦点问题.随着生活水平的提高和医疗卫生条件的改善,人类死亡率呈下降趋势,寿命不断延长.1981—2010年,根据《中国统计年鉴》数据显示,我国人均寿命从66.77岁上升至74.83岁,如果按同样的速度增长,到2100年,我国的人均寿命将超过95岁.老年人口死亡率的准确预测为我国社会养老及医疗卫生预算提供了一定的理论依据.
目前,人类死亡率预测模型主要有2类,分别为Lee-Carter模型及其改进和时间序列模型.Lee-Carter模型给出了不同年龄的对数死亡率关于时间的函数关系,其得到了广泛的应用,是当今世界上最流行的死亡率预测模型.但其也有一定缺陷,用一个模型来模拟所有年龄人口死亡率,只能有局部代表意义,一些年龄模型的误差较大,其人口死亡率预测不准确.文献[1]以中国人口生命表为基础,对2010年的人口按龄死亡模式进行修正,研究发现2010年中国人口死亡率下降至5.58‰.文献[2]介绍了预测死亡率常用的Lee-Carter模型的应用,估计其方法及预测原理,并选用该模型对我国未来人口死亡率进行了预测,结果表明未来人口死亡率将持续降低.文献[3]对Lee-Carter模型进行了完整的理论研究,并给出了完整的Lee-Carter模型理论分布和区间预测表达式,相比于传统Lee-Carter预测方法,得到的预测区间较宽,长寿风险评估更为准确.基于以上讨论并结合以往国内外学者对人口死亡率的研究,本文采用时间序列分析的方法对60~110岁老年人口死亡率进行了研究.首先对原序列采用k-means聚类的方法,利用余弦相似度对不同年龄死亡率进行分类,进而对每一类分别进行分析建立模型,弥补了直接建模带来的不足.相对以往研究,此方法建立的模型误差较小,预测结果更为精确.
1 原时间序列的聚类分析
1.1 k-means聚类的基本思想
聚类分析是直接比较各事物之间的性质,将性质相近的归为一类,性质差别较大的归为不同的类,以使簇内有较高相似度,而簇间相似度较低[4].本文聚类采用k-means聚类,其基本思想是:从n个数据中任意选取c个对象用来作初始聚类中心,每个对象初始的代表一个簇的平均值或者中心,剩余n-c个对象,根据其到各个簇的距离,将它们归类到距离最小的簇中心,然后重新计算每个簇的平均值,重复此过程,直至聚类准则函数收敛;准则函数通常为平方误差准则:
(1)

1.2 余弦相似度
本文k-means聚类中距离采用余弦相似度度量.余弦相似度是用向量空间中2个向量的夹角余弦作为衡量2个向量之间的贴合程度,其相似度度量为:
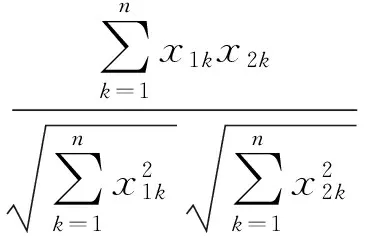
(2)
其中,x1k,x2k为2个向量第k维的值,n为向量的个数,且cosθ的取值范围为[0,1].余弦值越大,对象间的相似度越大;余弦值越小,对象间的相似度越小.
2 自回归移动平均模型
本文选用自回归移动平均模型即ARMA模型[5],它是由自回归模型AR和移动平均模型MA组成,其基本公式为:
yt=φ1yt-1+φ2yt-2+…+φpyt-p+et-θ1et-1-…-θqet-q
(3)
其中,p为自回归模型的阶数,φi为自回归系数,yt-i为时间序列在t-i期的观察值,et为不能用模型说明的随机扰动,q为移动平均模型的阶数,θi为移动平均系数,et-i为第t-i个时期进入系统的随机扰动.建立ARMA模型要求时间序列具有平稳性.原序列是不平稳的,通过差分使序列达到平稳;经过差分后建立的ARMA(p,q)模型称为求和自回归移动平均模型即ARIMA(p,d,q).
3 人口死亡率建模分析
3.1 数据分析与处理
本文研究的老年人口死亡率数据从http://www.mortality.org/下载,数据为1963—2014年60~110岁人口死亡率,文中所有算法实现都是由R语言来实现.数据较多,首先对数据采用k-means聚类方法.由于考虑到人口死亡率的走势图,将1963—2014年死亡率走势相近的年龄聚为一类.这样,每类建立一个模型,并用该模型预测该类中其他年龄死亡率.基于以上特点,聚类中的距离采用余弦相似度,将数据聚为3类,分别为60~80岁、81~90岁、91~110岁.
分别对3类数据采用时间序列方法进行分析.分别选取62岁、86岁和94岁数据作为每一类的代表序列进行建模,选取1963—2006年数据作为建模样本,2007—2014年数据作为测试样本来评估模型的优劣,并由模型预测2015—2020年老年人口死亡率.由R软件的单位根检验函数adf.test知,62岁、86岁和94岁死亡率数据的置信水平P值依次为0.838 8,0.380 7和0.539 5,从而数据为非平稳序列.接着对序列进行一阶差分得到的新序列Yt的P值依次为0.021 2,0.202 5和0.156 0,从而得到62岁的一阶差分序列为平稳序列,但86岁和94岁的一阶差分序列为非平稳序列.然后再对86岁和94岁数据进行二阶差分,得到序列的P值均为0.010 0,则其为平稳序列.
3.2 模型建立与检验
3.2.1 模型诊断
模型诊断主要包括显著性检验和残差分析等[6].参数显著性检验就是检验参数是否显著异于零.如果参数不显著,说明影响不明显,将其从模型中删除;如果参数显著异于零,则将其保留在最终模型中.对于ARMA(p,q)模型,标准化残差为:
(4)
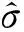
H0:ARMA(p,q)是充分的.
H1:ARMA(p,q)是不充分的.
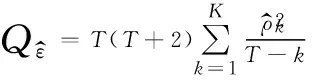
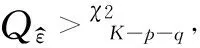
3.2.2 模型建立与检验
经过差分并由ADF检验得到62岁为一阶平稳序列,86岁和94岁为二阶平稳序列,即62岁、86岁和94岁序列的d分别为1,2,2,且新序列的ACF和PACF如图1所示.
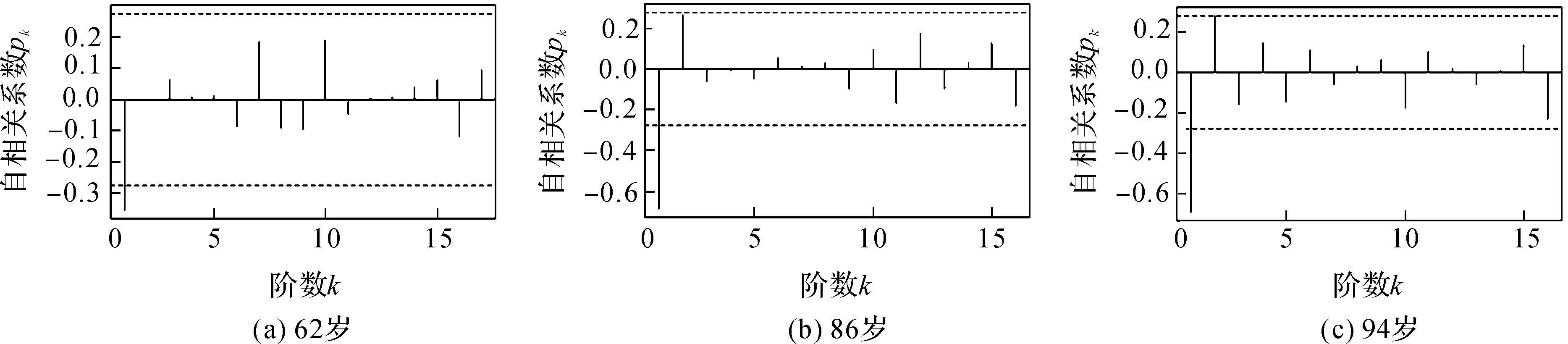
图1 ACF图
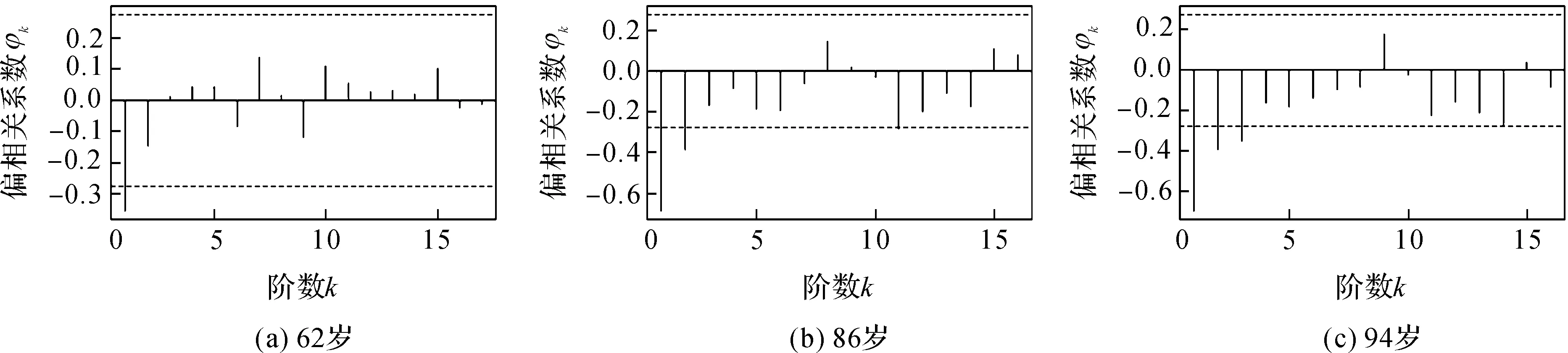
图2 PACF图
由图1、图2可以看出,新序列的自相关函数和偏自相关函数都是拖尾的[7],因此可建立ARMA模型,计算所有模型的AIC值,记下AIC最小时所对应的p,q.对62岁序列,当p=1,q=2时,AIC值最小,故此模型为ARIMA(1,1,2);而86岁和94岁序列都是当p=1,q=1时,AIC值最小,故这2类模型均为ARIMA(1,2,1).对模型的参数进行最小二乘估计,得到估计参数结果如表1所示.

表1 3个模型的参数估计
在表1中,ARIMA(1,1,2)62,ARIMA(1,2,1)86和ARIMA(1,2,1)94分别为62岁、86岁和94岁老年人口死亡率模型的参数估计,从数值中可以看出,对于任一模型,参数都显著异于零,则由参数显著性检验知参数对模型影响显著.
然后用这3类模型分别预测2007—2014年62岁,86岁和94岁老年人口死亡率,预测结果如图3所示.
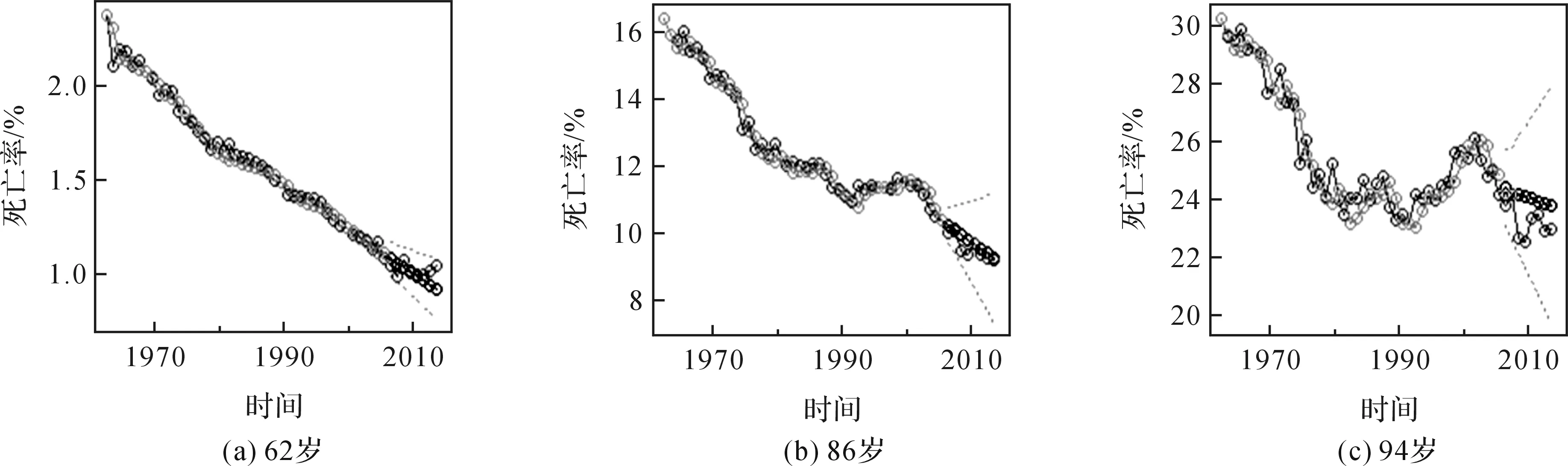
图3 老年人口死亡率预测值、真实值及拟合值
从图3中可以看出,3个模型对于2007—2014年数据拟合效果较好,预测值与真实值在误差允许的范围内几乎接近一致.进一步通过sarima函数检验3类模型的残差自相关性,3类模型的白噪声方差估计值分别为0.001 8,0.078 2,0.460 4.Ljung-Box统计量结果表明,3类模型均在自由度为6的情况下,残差已经不存在自相关性,且P值分别为0.216 8,0.140 6和0.151 0,所有值远远大于5%,则残差有很好的独立性.由模型诊断的理论可知,这3类模型都是正确设定的.其中94岁模型的死亡率出现突然上升的情况,并且上升的时间正好处于2003年附近,这与此时间段内发生的非典疫情相吻合,而该年龄的人口基数小导致上升的最为明显.
3.2.3 类模型的误差分析
对上述所建3类模型进行误差分析,分别用R软件计算出模型误差与检验误差,来检验模型的优劣.3类模型的模型误差与检验误差如表2所示.

表2 3个模型的模型误差与检验误差
从表2可以看出,3类模型中,模型误差和检验误差都比较小,则表明样本内拟合精度和检验样本预测精度都比较高,进一步说明所建模型是正确的.
3.3 老年人口死亡率预测值
由以上分析,3类模型样本内拟合精度和检验样本预测精度都比较好,实验结果表明该模型构造是充分的,所以其可用于预测.分别用此模型预测2015—2020年老年人口死亡率,如表3所示.

表3 2015—2020年老年人口死亡率预测值 %
由于聚类所选距离设定为余弦相似度,因此,其他年龄人口死亡率可代入相关参数来预测.由于模型样本内拟合精度和检验样本预测精度都比较高,所以此预测值具有一定的参考意义.
4 结束语
本文提出了用ARIMA模型预测老年人口死亡率.通过研究表明,所建立的模型能较为准确地描述老年人口死亡率所呈现的特征,为保险公司企业退休金及商业保险提供了理论依据,对其制定决策有一定的参考价值;其次,预测值对国家社会养老保险及医疗卫生预算也有重大意义.
[1] 张文娟,魏蒙.中国人口的死亡水平及预期寿命评估——基于第六次人口普查数据的分析[J].人口学刊,2016,38(3):18-28.
[2] 苏华,赵文.我国死亡率预测与长寿风险[J].经营管理者,2016,31(6):3-4.
[3] 王志刚,王晓军,张学斌.Lee—Carter模型的理论分布和区间预测[J].数理统计与管理,2016,35(3):484-493.
[4] TAN P N,STEINBACH M,KUMAR V.数据挖掘导论(完整版)[M].北京:人民邮电出版社,2011:310-314.
[5] Cryer J D,Chan K S.时间序列分析及应用[M].潘红宇,译.北京:机械工业出版社,2011:63-133.
[6] 赵华.时间序列数据分析:R软件应用[M].北京:清华大学出版社,2016:58-88.
[7] 于宁莉,易东云,涂先勤.时间序列中自相关与偏相关函数分析[J].数学理论与应用,2007,27(1):54-57.
ModelingandAnalysisoftheMortalityoftheElderlyPopulation
HUANG Peipei, ZHENG Jing
(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
From 1963 to 2014 at the age of 60 to 110 year old population mortality based on the K-means clustering method, the cosine similarity as the distance function, which will be grouped into 3 categories, each kind of modeling method based on time series analysis. In each class was selected at the age of 62, 86 and 94 year old mortality data, the data from 1963 to 2006 were used to model and test the model with the data from 2007 to 2014. The fitting precision and prediction accuracy of test samples are good, which verifies the effectiveness and feasibility of the model. This model is also used to predict the class of 2015 to 2020 the elderly population mortality.
mortality; K-means clustering; ARIMA model
O213
A
1001-9146(2017)05-0092-05
2016-12-14
黄佩佩(1992-),女,山东济宁人,硕士研究生,统计学.通信作者:郑静副教授,E-mail:zhengjing@hdu.edu.cn.
10.13954/j.cnki.hdu.2017.05.017

