基于粒子群优化的PID控制器设计与研究

王 欣，葛恒清

(淮阴师范学院物理与电子电气工程学院，江苏淮安 223300)

基于粒子群优化的PID控制器设计与研究

王 欣，葛恒清

(淮阴师范学院物理与电子电气工程学院，江苏淮安 223300)

本文针对PID控制器参数整定的问题，提出了一种基于粒子群优化的PID控制器设计方法。首先建立PID控制器仿真模型，然后将待优化的三个参数(KP、KI和KD)作为粒子群中的粒子，采用误差绝对值时间积分函数ITAE作为优化目标，将PID控制器参数整定问题转化为优化问题，最后将设计好的PID控制器进行仿真实验。仿真结果表明，该方法与传统的整定方法相比，具有更好的动态响应特性和满意的控制效果，进而验证了该方法的可行性和有效性。

PID控制器；粒子群优化；参数整定

PID控制器具有结构简单、易于实现、可以应用于大多数控制对象等优点。PID控制是控制系统中应用最为广泛的一种控制规律。采用不同的PID参数整定方法，其控制效果和性能将大不相同，因此，对PID控制参数整定方法的研究具有重要的意义[1]。传统的PID参数整定方法有简易工程法、优选法、试凑法、自整定法等，这些传统的方法往往难以获得最优的PID参数。学者们也提出了很多智能优化算法，如遗传算法、神经网络等，但这些算法也存在明显的缺陷[2-3]。如遗传算法需要进行编码和解码，过程较为繁琐，且计算量大，不易实现；神经网络需要大量的已知训练样本，且容易陷入局部最优等问题。

粒子群算法是一种全局随机优化算法，具有算法简单、寻优能力强、鲁棒性好等优点，在各种寻优问题中应用较为广泛[4]。为了解决PID控制器参数难以整定到最优的问题，本文提出了一种基于粒子群优化的PID参数整定方法，在Matlab和Simulink环境下进行了仿真实验，并将仿真结果同传统的PID整定方法进行比较，结果表明了该方法的可行性和优越性。

1 PID控制器原理

1.1 模拟PID控制器

PID控制是比例(Proportional)、积分(Integral)和微分(Derivative)控制的简称，是控制系统中应用最为广泛的一种控制规律[5-6]。常规的PID控制框图如图1所示。

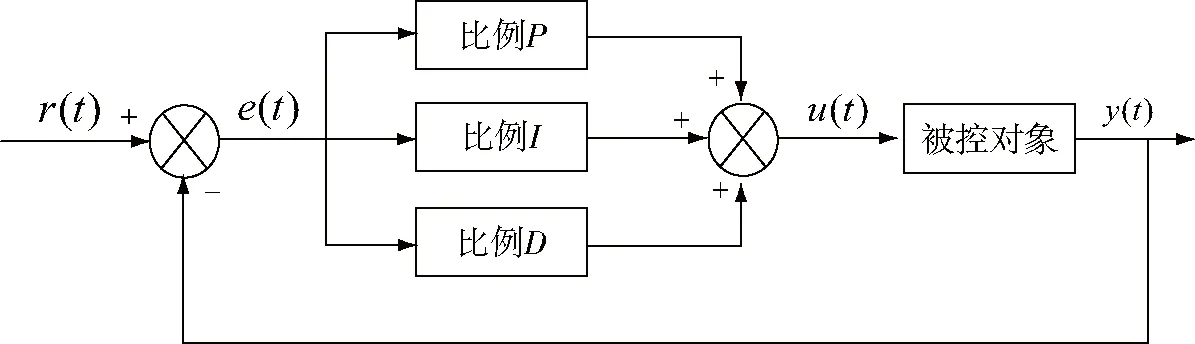
图1 常规的PID控制框图

PID控制器是通过对系统给定值r(t)和输出y(t)之间的偏差e(t)进行比例、积分和微分，然后输出控制量u(t)作用于被控对象，通过调节控制量u(t)，使得偏差e(t)趋于0，从而保证控制系统处于一个预期稳定状态。其控制规律为：

(1)

其中，u(t)为PID控制器的输出；KP为比例增益；TI为积分时间常数；TD为微分时间常数；e(t)为系统给定值与输出的偏差。

对应的模拟PID的传递函数为：

(2)

1.2 数字PID控制器

为了便于通过计算机实现PID控制，需要将模拟PID离散化为差分方程。其转换结果如下：

(3)

其中，u(k)为采样时刻k时的输出值；e(k)为采样时刻k时的偏差；e(k-1)为采样时刻k-1时的偏差；k为采样序列；T为采样周期。

式(3)中u(k)表示了执行机构的位置，称为数字PID位置型控制算式。位置型控制算式在工业过程控制中应用较少，这是因为要累加偏差e(k)，不仅要占用较多的存储单元，而且较难通过程序实现。因此，需要对其进行改进，产生数字PID增量型算式。由式(3)可得：

(4)

由式(3)和式(4)可得数字PID增量型算式为：

Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)].

(5)

其中，KI=KPT/TI为积分系数；KD=KPTD/T为微分系数。

1.3 PID参数对控制性能影响

1.3.1 比例系数KP

增大比例系数会加快系统的响应速度，减小系统的稳态误差，使系统的控制精度得以提高。过大的比例系数KP会使系统产生超调和振荡并使调节时间加长；过小的KP又会使系统反应过慢。

1.3.2 积分系数KI

一般不单独采用积分控制器。增大积分系数可以减小振荡，使系统更加稳定，但系统消除静差的时间被延长；减小积分系数会使系统的振荡次数变多，降低系统的稳定性。

1.3.3 微分系数KD

微分控制可以减小超调量，提升系统的稳定性，其只对动态过程起作用，对稳态过程没有影响。微分控制对系统的噪声很敏感，所以一般不单独采用微分控制器。

PID控制器中的三个参数KP、KI和KD将直接影响控制效果的优劣，所以对PID控制器进行设计本质上就是对PID的三个参数进行选择。

2 粒子群算法原理

粒子群算法(PSO)是由Kennedy和Eberhart博士在1995年所提出的一种群体智能随机优化算法，该算法是通过模拟鸟群的觅食行为发展而来的，具有算法简单、收敛速度快和鲁棒性好等优点[7]。

在PSO算法中，每个优化问题的潜在解相当于是搜索空间中一个点，称之为“粒子”，粒子的好坏是由适应度函数所决定的，每个粒子都有一个速度决定其飞行的方向和速率大小，粒子们通过跟随种群中的最优粒子在解空间中进行搜索。

PSO首先初始化一群随机粒子，然后通过不断迭代来寻求最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己的速度和位置，一个是粒子自身极值Pbest，一个是种群全局极值Gbest。粒子在搜索空间中的速度和位置由如下公式进行确定。

(6)

(7)

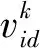
为了减少粒子在搜索的过程中飞出规定搜索空间的可能性，需要对粒子的飞行速度和位置进行限制，在迭代的过程中，当其超出边界值时，则取边界值。

3 PSO优化PID算法设计

3.1 基本思想

将PID控制器中的三个参数KP、KI和KD组合在一起作为一个“粒子”，在给定的搜索空间中，每一个粒子以一定的速度飞行，在飞行的过程中，每个粒子将根据个体的飞行经验和群体的飞行经验动态的调整自己的速度和位置，从而逐步逼近最优目标。PSO优化PID的系统结构如图2所示。PSO根据系统的运行状态，不断地调整PID的三个参数，从而使控制系统的性能指标和控制效果达到最优。

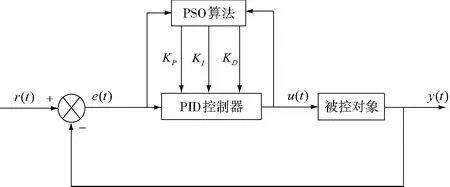
图2 PSO优化PID的系统结构图

图3 PSO优化PID的系统结构图

利用PSO算法优化PID控制器的原理为：PSO随机初始化粒子种群，并将该种群中的粒子依次赋值给PID控制器的三个参数，然后运行在Simulink中所搭建的PID模型，得出该组粒子所对应的适应度值，最后判断是否退出算法。

3.2 适应度函数的确定

PID控制器的优化设计就是选择合适的KP、KI和KD，使得系统各项性能指标和控制效果达到最优。在控制系统中，常用的误差性能指标有ISE、ISTE和ITAE，本文选用误差绝对值时间积分函数ITAE指标作为目标函数，其定义为：

(8)

其中，t为时间；e(t)为系统给定值与系统输出的偏差。

3.3 PSO优化PID算法流程

采用PSO算法优化PID三个参数的基本流程如下：

Step1：初始化粒子种群。给出PID三个参数的取值范围，在此范围内随机初始化N个粒子，包括粒子的速度和位置、惯性因子ω、加速常数c1和c2、最大迭代次数、最小适应值、个体极值和全局极值等；

Step2：按照式(8)计算种群中每个粒子的适应度值；

Step3：对每一个粒子，如果其适应度值优于该粒子的个体极值Pbest，则将其作为当前的Pbest；对每一个粒子，如果其适应度值优于全局极值Gbest，则将其作为当前的Gbest；

Step4：按照式(6)和式(7)对粒子的飞行速度和位置进行更新，并对超出速度和位置范围的粒子进行处理；

Step5：如果达到最大迭代次数或其适应度值小于所设定的适应度值下限，则转入Step6，否则转入Step2；

Step6：得到最优的PID参数，算法结束。

通过上述分析，基于PSO优化PID控制器的算法流程如图3所示。

4 仿真实验

本文采用Matlab来实现PSO算法，利用Simulink来搭建仿真模型文件，在运行PSO算法的过程中不断调用PID仿真模型，以此来实现PID参数的优化计算。

4.1 仿真实例

为了验证本文的优化效果，选用参考文献[5]中的被控对象传递函数：

(9)

在仿真实验中，粒子群算法的参数选择如下：粒子群规模N=100；惯性因子ω=0.6；加速常数c1=c2=2；最大迭代次数k=100。

4.2 仿真模型图

在Simulink下建立PID优化设计的仿真模型，如图4所示。图4中上半部分为目标函数即粒子群算法中的适应度函数(ITAE)的求取；下半部分为PID模型，积分环节采用积分器，微分环节采用微分串联一阶惯性环节，从而构成了不完全微分PID控制器。

图4 PID优化设计仿真模型图

4.3 仿真结果

为了验证本文所提出的基于粒子群算法优化PID控制器的优越性，将粒子群算法优化PID的结果同传统的PID整定的临界比例度法(Z-N)进行比较，其参数和性能指标如表1所示，其所对应的系统单位阶跃响应曲线如图5所示。

表1 不同优化方法所对应的参数及性能指标

图5 不同优化方法所得参数所对应的系统单位阶跃响应曲线

从表1和图5可得，本文所提出的基于PSO优化的PID控制器具有调节时间短、超调量小的动态性能，具有较好的控制品质。相对于临界比例度法(Z-N)等传统的PID参数整定方法，利用粒子群优化的PID控制器的各项性能指标均显著提升，优化目标ITAE的值更小。因此，该方法可以广泛地应用于工业PID控制系统的设计。

5 结语

针对传统的PID整定方法难以获得最优参数的问题，本文提出了一种基于粒子群优化的PID控制器设计方法。仿真结果表明，通过该方法所设计的PID控制器与传统的设计方法相比，具有更好的动态响应特性和满意的控制效果。由于粒子群算法具有易于实现、寻优速度快和全局收敛等诸多优点，因此该方法具有较好的应用前景。

[1]白金,韩俊伟.基于MATLAB/Simulink环境下的PID参数整定[J].哈尔滨商业大学学报:自然科学版,2007(6):673-676,681.

[2]郭庆鼎,李蒙,郭威.PID控制器参数的遗传算法优化设计[J].沈阳工业大学学报,2000(1):31-33.

[3]王俊国,王永骥,万淑芸.基于动态神经网络的PID参数整定与实时控制[J].系统工程与电子技术,2004(6):777-778,810.

[4]安凤栓,常俊林,苏丕朝,等.基于改进粒子群优化算法的PID控制器参数优化[J].工矿自动化,2010(5):54-57.

[5]王素青,姜维福.基于MATLAB/Simulink的PID参数整定[J].自动化技术与应用,2009(3):24-25,28.

[6]张家骏.基于粒子群算法的PID控制器参数优化研究[J].计算机仿真,2010(10):191-193,222.

[7]Kennedy J,Eberhart R.Particle swarm optimization[C].IEEE International Conference on Neural Networks, Proceedings,IEEE Xplore,1995(4):1942-1948.

DesignandResearchofPIDControllerBasedonParticleSwarmOptimization

WANG Xin, GE Heng-qing

(School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huai’an Jiangsu 223300, China)

A design method based on particle swarm optimization was proposed for tuning PID controller parameters. Firstly, the simulation model of PID controller was established, and then the three parameters(KP、KIandKD) to be optimized were taken as particles on particle swarm, the integrated time and absolute error(ITAE) was taken as optimization objective, and the problem of tuning PID controller parameters was translated into optimization problem, finally, the designed PID controller was simulated. The simulation results showed that this method has better dynamic response characteristics and satisfactory control effect than traditional tuning method, Furthermore, the feasibility and validity of the method were verified.

PID controller; particle swarm optimization; parameters tuning

TP214

A

2095-7602(2017)10-0040-05

2017-05-11

江苏省前瞻性联合研究项目“智能通用型谷物色选干燥一体机研制及其产业化”(BY2016062-01)；淮安市产学研协同创新项目“智能通用型谷物色选机研制”(HAC201605)。

王 欣(1985- )，男，实验师，硕士，从事智能控制算法应用研究。