基于遗忘因子递推最小二乘的SPMSM稳态多参数辨识

刘金海

(闽南师范大学物理与信息工程学院，福建漳州 363000)

基于遗忘因子递推最小二乘的SPMSM稳态多参数辨识

刘金海

(闽南师范大学物理与信息工程学院，福建漳州 363000)

在矢量控制基础上，应用遗忘因子能够递推最小二乘(FFRLS)系统辨识算法，本文提出一种关于面装式永磁同步电机(SPMSM)的稳态多参数辨识新方法。新方法可以同时辨识SPMSM的电阻、电感和永磁磁链3个电机参数。在Simulink环境下对新方法进行仿真，仿真结果验证了新方法的准确性，显示新方法的辨识精度高。

遗忘因子递推最小二乘；永磁同步电机；多参数辨识

永磁同步电机(PMSM)，具有体积小、效率高、重量轻、转矩电流密度比高、易维护等特点，广泛应用于激光加工、机器人、数控机床、大规模集成电路制造、雷达和各种军用武器等[1-4]。永磁同步电机参数辨识技术对其闭环控制参数优化、无位置传感控制、状态监测与故障诊断等具有重要意义。常见的辨识方法主要有MRAC或MRAS(模型参考自适应控制或系统)[5]、KF或EKF(卡尔曼滤波或扩展卡尔曼滤波)[6]、人工神经网络(ANN)[7]、RLS(递推最小二乘)[8]、GA(遗传算法)及其它仿生智能进化类方法等。

本文在矢量控制基础上，通过面装式永磁同步电机(SPMSM)负载转矩和直轴电流的多稳态构造，建立满秩型稳态多参数辨识模型，应用遗忘因子递推最小二乘(FFRLS)[9]系统辨识算法，提出一种关于SPMSM的稳态多参数辨识新方法。新方法可同时辨识SPMSM的电阻、电感和永磁磁链。在Simulink环境下进行仿真验证，仿真结果表明新方法辨识精度高，具有较好的工程应用价值。

1 满秩型稳态多参数辨识模型

多参数辨识模型是永磁同步电机多参数辨识的基础。辨识模型应是满秩的而非欠秩的，这是永磁同步电机多参数辨识的辨识结果正确全收敛的理论保障。多参数辨识模型是基于永磁同步电机数学模型的电压方程。永磁同步电机dq坐标系下的动态电压方程如式(1)所示：

(1)

(1)式可据辨识需要改写成状态方程形式，如式(2)；或一阶离散差分方程形式，如式(3)。

(2)

(3)

稳态辨识时，式(1)电流微分项为零，可改写为式(4)：

(4)

面装式永磁同步电机，交直轴电感相等，Ld=Lq=L，式(4)改写为：

(5)

所要辨识的面装式永磁同步电机参数有3个：定子电阻Rs、定子电感L、永磁磁链ψm，这3个参数都出现在交轴稳态电压方程式(6)中，因此，只需对交轴稳态电压方程进行多稳态实例化构造，即可构造满秩型稳态多参数辨识模型。

uq=Rsiq+ωeLid+ωeψm.

(6)

为了3参数辨识下达到满秩，应构造3种线性无关的稳态工作条件，分别对电机的负载转矩和直轴电流进行双稳态组合，得到图1中的D1、D2、D3稳态区域。D1状态(id1,iq1,ωe1)、D2状态(0,iq1,ωe1)、D3(0,iq3,ωe1+ωer)。

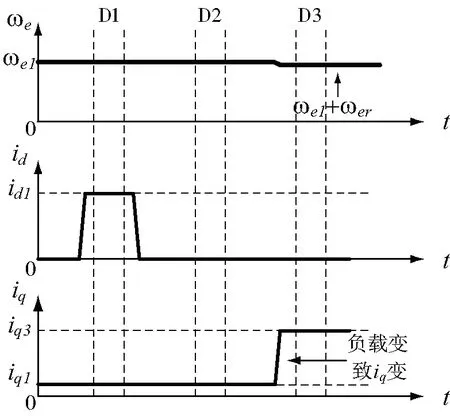
图1 多稳态波形示意图

假定3种状态下的uq分别为uq1、uq2、uq3，代入式(6)多稳态实例化得式(7)。

(7)

(7)式即为满秩型稳态多参数辨识模型。

2 多参数辨识方法原理

式(7)多参数辨识模型为线性无关的三元一次方程组，有唯一解，说明模型是满秩的，其解为：

(8)

由式(8)可直接求解辨识出3个参数，然而基于3点数据式的求解方式辨识抗干扰能力、可靠性较差，多参数辨识通常采用相关的递推辨识算法，以数据带迭代辨识方式则更可靠有效，如常用的遗忘因子递推最小二乘(FFRLS)辨识算法。FFRLS具有易理解、通用性好、辨识效果好等特点，其递推公式为[9]：

(9)

(10)

参照图1，将图中的D1～D3数据逐组迭代入辨识器式(9)和式(10)进行计算，辨识迭代过程相当于自动对式(7)求解逼近。假定D1、D2、D3各含N组数据，FFRLS稳态多参数辨识算法流程图如图2所示。

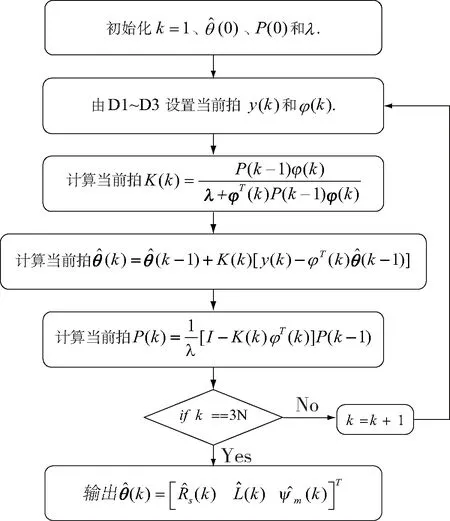
图2 FFRLS稳态多参数辨识算法流程

3 仿真与分析

采用Matlab/Simulink仿真工具，根据上述辨识方法原理进行仿真，仿真电机参数如表1所示，采用矢量控制、SVPWM调制方式、FFRLS辨识算法，仿真设计图如图3所示。选择相应的状态条件进行稳态满秩辨识，转速阶跃给定3000 r/min，选择相关时间点，注入直轴电流id阶跃给定6A、注入负载转矩TL扰动给定值1N.m，仿真所得电机工作波形如图4所示。

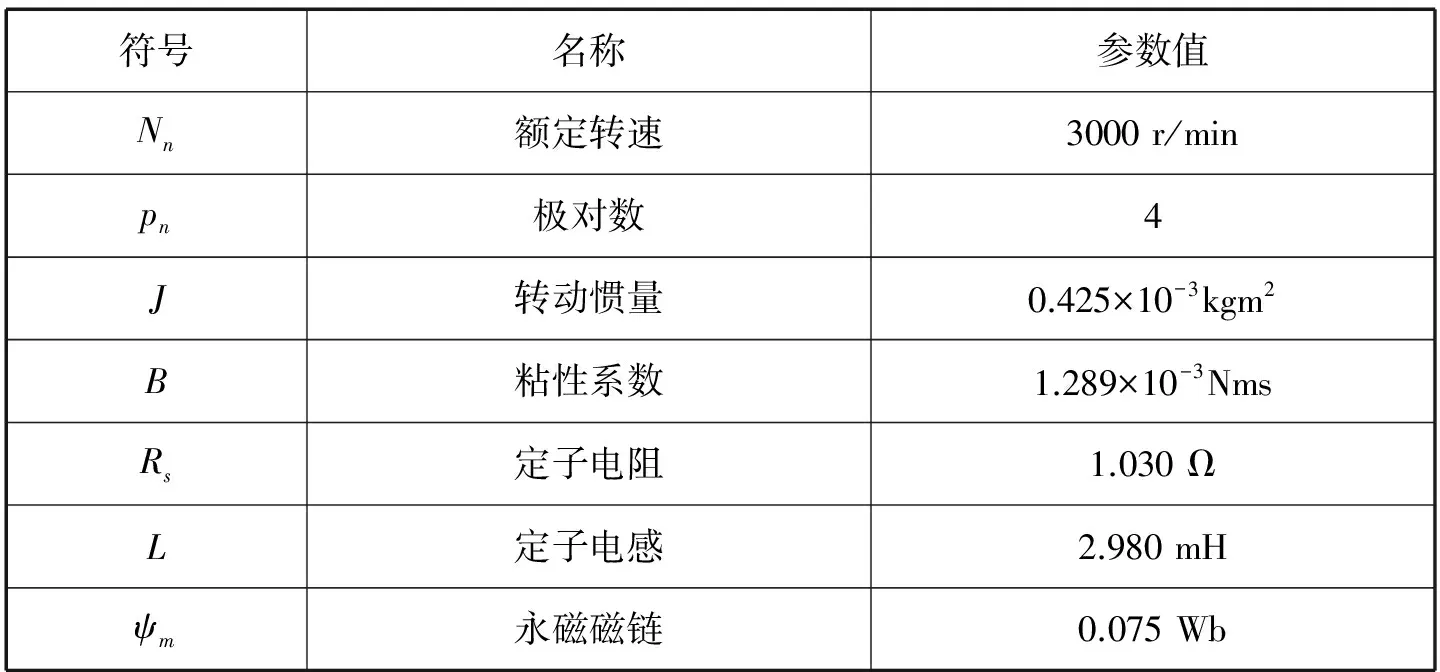
表1 仿真电机参数

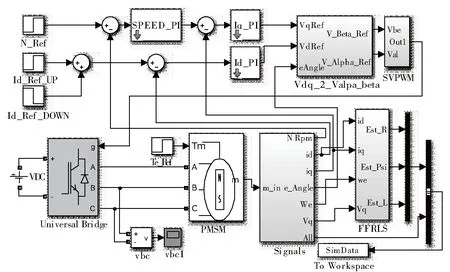
图3 FFRLS稳态多参辨识仿真设计界面

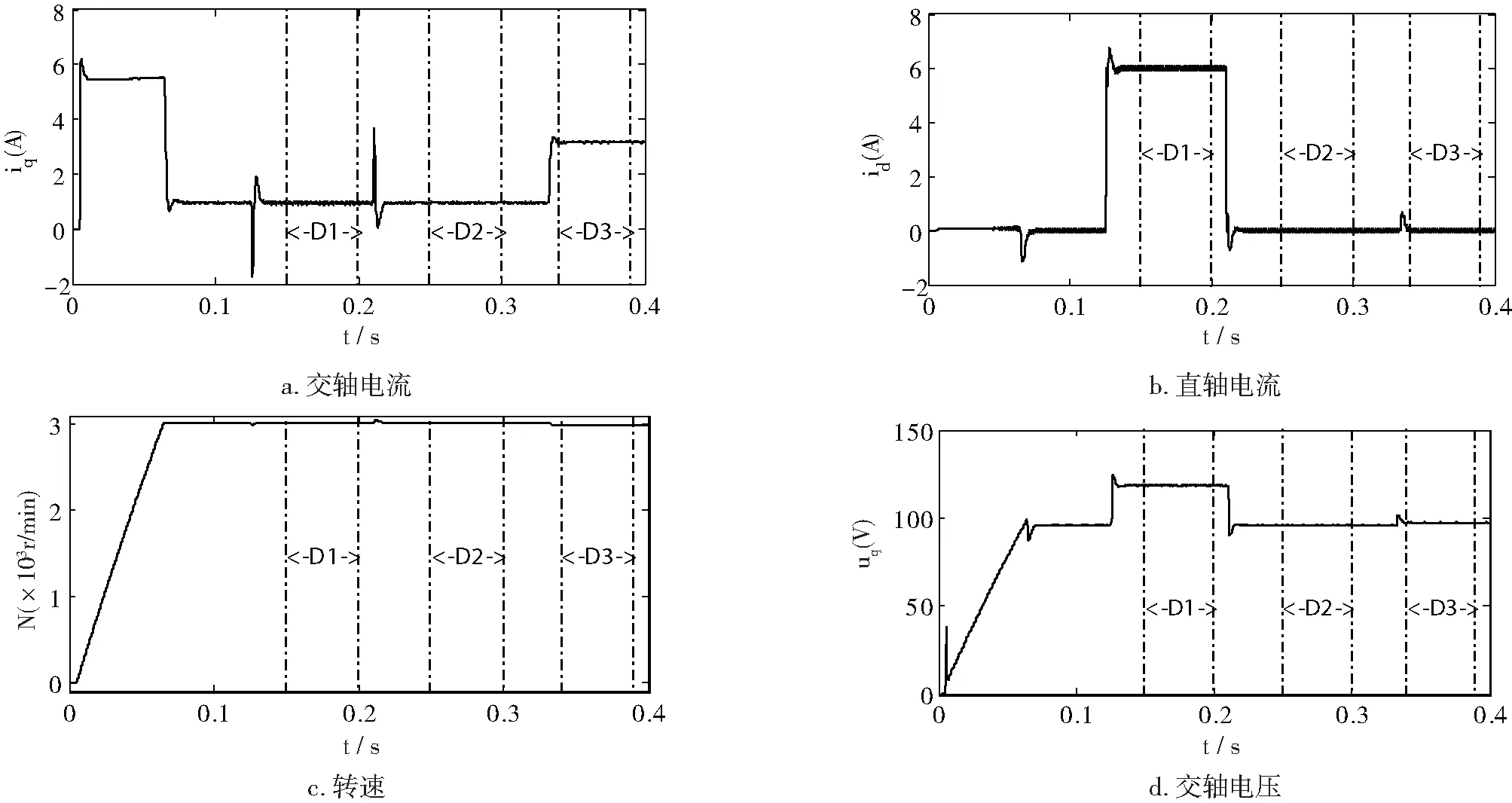
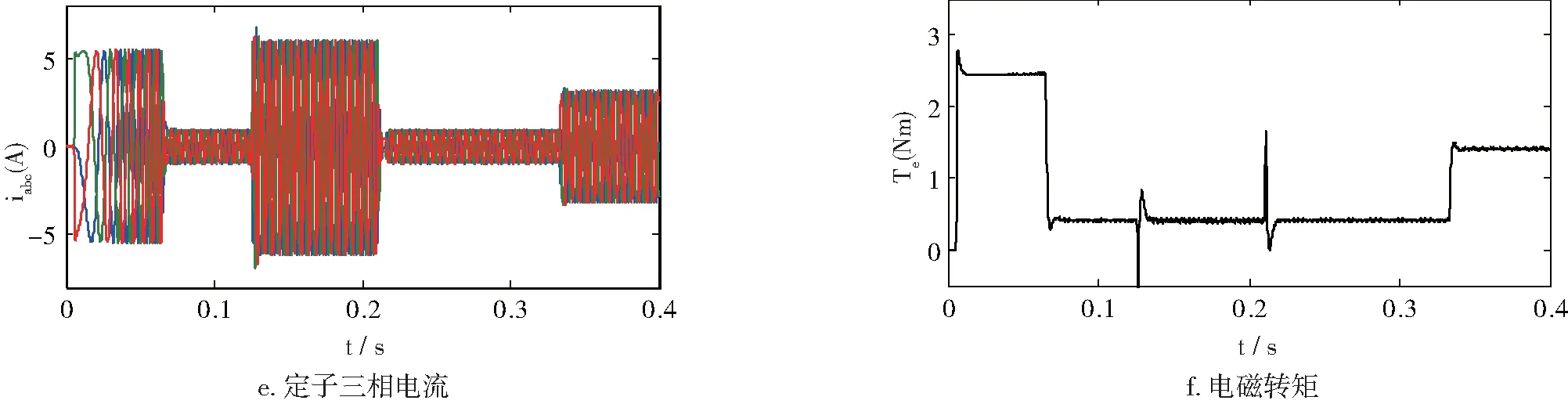
图4 仿真所得电机状态波形

由图4仿真所得电机工作波形可见，电机在矢量控制下，转速快速响应上升到给定值，t=0.125s左右直轴电流id快速响应上升到6A给定值；t=0.33s左右电磁转矩Te上升到1.4N.m左右，大于负载转矩给定值1N.m，这是因为存在电机粘性阻力矩，与表1中参数B有关；t=0.33s左右在负载转矩的扰动下，转速出现较小的扰动稳态误差。总体而言，各工作波形响应正常，响应性能较好。

对应图4波形结果，将图中数据带D1、D2、D3状态数据输入FFRLS多参数辨识器，仿真所得辨识值结果波形如图5所示。

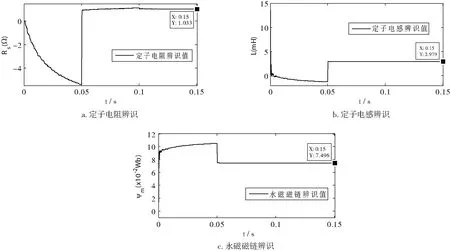
图5 仿真所得稳态满秩参数辨识值波形

由图5可以看出，过了全部时间的2/3之后(数据带D1、D2迭代完，进入D3数据带)，3个参数辨识值全部快速正确收敛，这是因为辨识数据状态满秩；然而，在前2/3时间(数据带D1、D2内)内，3个参数辨识值部分收敛，这是因为辨识数据状态欠秩，实际的辨识模型只相当于式(7)的前两个子方程。

电机参数辨识值仿真结果如表2所示，定子电阻、定子电感、永磁磁链的辨识误差分别为0.29%、0.03%、0.05%，可见辨识精度较高，从仿真角度验证了新方法是有效可行的。

4 结语

综上所述，通过SPMSM负载转矩和直轴电流的多稳态构造，建立了秩数为3的满秩型稳态多参数辨识模型。基于FFRLS系统辨识算法，本文提出一种关于SPMSM的稳态多参数辨识新方法。该方法能够同时辨识SPMSM的电阻、电感和永磁磁链3个参数。在Simulink下仿真验证了新方法是可行有效的，仿真结果表明新方法辨识精度高，具有较好的工程应用价值。

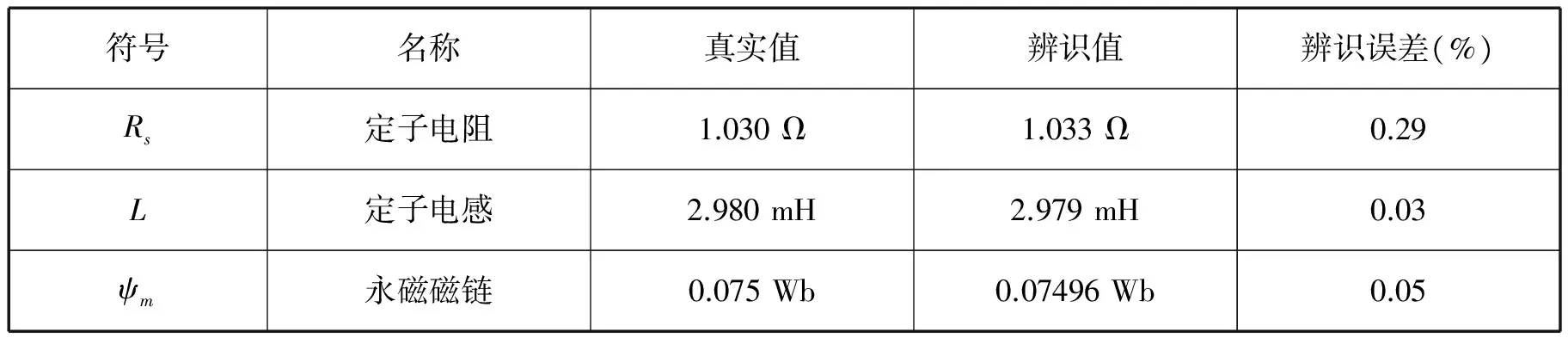
表2 电机参数辨识值仿真结果

[1]Pillay P,Krishnan R.Modeling,simulation,and analysis of permanent-magnet motor drives.I.The permanent-magnet synchronous motor drive[J].IEEE Transactions on Industry Applications,1989(2):265-273.

[2]刘金海,陈为.表贴式永磁同步电机准稳态多参数在线辨识[J].电工技术学报,2016(17):154-160.

[3]刘金海,陈为,胡金高.永磁同步电机dq电感参数新实验获取法[J].电工技术学报,2014(7):97-103.

[4]唐任远.现代永磁电机与理论[M].北京:机械工业出版社,1997:4-10.

[5]Zhang Y,Yin Z,Sun X,et al.On-line identification methods of parameters for permanent magnet synchronous motors based on cascade MRAS[C].IEEE International Conference on Power Electronics and ECCE Asia,2015:345-350.

[6]Salvatore L,Stasi S.Application of EKF to parameter and state estimation of PMSM drive[J].IEEE Proceedings B-Electric Power Applications,1992(3):155-164.

[7]Liu K,Zhu Z Q.Position-offset-based parameter estimation using the adaline NN for condition monitoring of permanent-magnet synchronous machines[J].IEEE Transactions on Industrial Electronics,2015(4):2372-2383.

[8]Underwood S J,Husain I.Online parameter estimation and adaptive control of permanent-magnet synchronous machines[J].IEEE Transactions on Industrial Electronics,2010(7): 2435-2443.

[9]庞中红,崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社,2013.

Multi-parameterIdentificationofSPMSMUnderSteadyStateBasedonForgettingFactorRecursiveLeastSquares

LIU Jin-hai

(Department of Physics and Electronic Information Engineering, Minnan Normal University,Zhangzhou Fujian 363000,China)

It is proposed a new method in the paper to identify multi-parameter of Surface Mounted PMSM (SPMSM) under steady state with the application of the system identification algorithm named forgetting factor recursive least squares (FFRLS) which is based on vector control. The new method can identify three parameters of SPMSM, which are resistance, inductance and permanent magnet flux-linkage. The method proposed is verified through simulation under Simulink environment whose results indicate high precision of the identification.

forgetting factor recursive least squares; permanent magnet synchronous machines; multi-parameter identification

TM351

A

2095-7602(2017)10-0016-06

2017-04-13

福建省教育厅基金项目“基于dSPACE现代电气伺服系统多参数在线辨识及其控制研究”(JA15299)。

刘金海(1982- )，男，讲师，博士，从事电力电子与电气传动研究。