无缆自主式水下机器人航向的模糊控制

于浩洋，李普强

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)

无缆自主式水下机器人航向的模糊控制

于浩洋，李普强

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)

针对自主式水下机器人各自由度之间相互耦合，其水下运动易受诸多外界环境干扰，运动具有强非线性，航向控制具有不稳定性等特点，建立近似的航向控制数学模型，设计出带有积分环节的模糊控制器，同时分析该模糊控制器的控制机理，给出积分模糊控制器的基本结构，在MATLAB /SIMULINK环境下进行了仿真验证，仿真结果表明这种控制方法能有效地提高控制系统的控制性能，具有较好的鲁棒性。

无缆；自主式水下机器人；航向；模糊控制；仿真

当前水下机器人已经成为替代人进行水下作业的重要工具，而其中无缆自主式水下机器人(Autonomous Underwater Vehicle，AVU)以其适应性强、智能化程度高、活动范围广等特点，更广泛地应用于水下作业, 受到各国各相关单位的高度重视[1-2]。由于AUV具有进退、浮潜、横移、横倾、纵倾、转艏6个自由度，各自由度之间相互耦合[3]。其运动控制涉及到航向、速度、深度、纵倾等诸多模块，水下运动易受海流、波浪、密度、压力等外界环境干扰，运动具有强非线性，再加之难以建立精确的数学模型，所以AUV的运动控制具有一定的难度[4]，而AUV航向控制又是其运动控制中的重要控制部分，精确的航迹控制是其水下作业的基础和前提，是水下规避障碍、定向巡航的重要保证。

本文提出利用带有积分环节的模糊控制(简称积分模糊控制)对其航向进行跟踪控制。

1 AUV航向运动建模

1.1 外形分析

AUV外形如图1所示，在AUV尾部装有用于改变航行速度的主推进器；用于改变AUV深度的水平舵的舵角；用于改变AUV航向的垂直舵，其中通过改变的舵角在其尾部产生艏摇力矩，使其做转艏运动来改变AUV的航向。本文只讨论通过尾部垂直舵舵角来改变航向的情况。

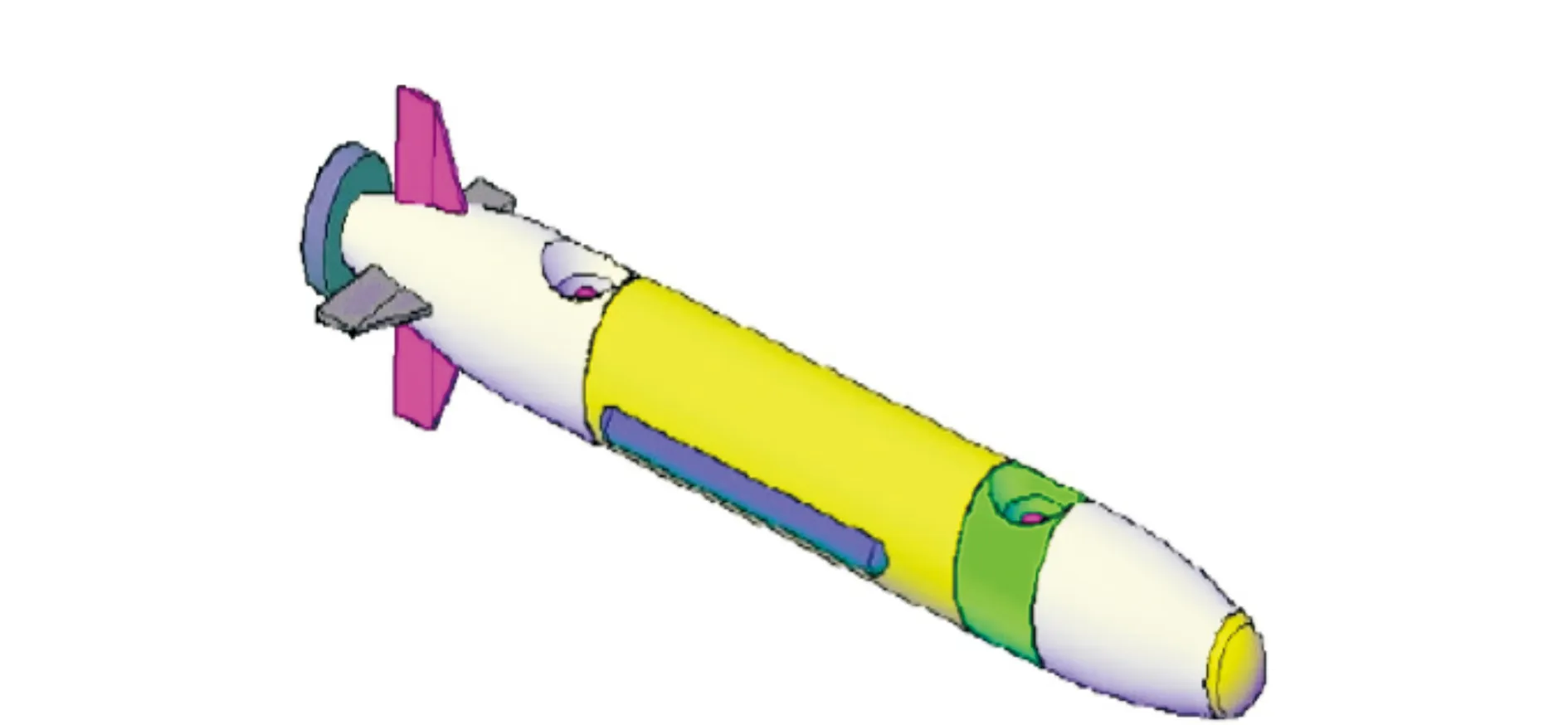
图1 AUV外形

1.2 建立坐标系

为便于分析AUV的航向控制问题，在水平面建立2个坐标系：一个是大地坐标系E-ξη，一个是艇体的运动坐标系O-XY，点E为地球上任意一点，E-ξ轴一般指向AUV的主航向，E-η轴与E-ξ轴垂直并且坐标面Eξη与水平面平行。点O选在AUV的重心上，O-X轴为AUV的纵轴心指向艇艏，O-Y轴与O-X轴垂直并且坐标面OXY与坐标面Eξη平行。AUV纵向速度为u(单位：m/s)，横移速度为v(单位：m/s)，艏摇角为Ψ(单位：rad)，艏摇角速度为r(单位：rad/s)，具体坐标系建立如图2所示。

图2 坐标系

1.3 航向运动数学模型

大地坐标系是惯性系，适用于牛顿力学定律，而艇体运动坐标系不是惯性坐标系，是为了方便分析AUV的水动力。在建立运动学模型时，应先在静坐标系也就是大地坐标系中建立航向运动数学模型，再通过一定的转换关系得到动坐标系中的航向运动数学模型。

水下机器人在水下所受的外力和力矩主要有推进力和力矩，操舵力和力矩，静水力和力矩，超重惯性力和力矩，流体动力和和力矩，环境作用力。忽略在垂直平面的作用力和力矩，结合AUV在水平面的运动特征方程，得出AUV在速度为定值时的航向运动数学模型[5]。

(1)

式中：

2 积分模糊控制器的设计

常规模糊控制器(单一的模糊控制器)，虽有相应速度快、适应性强等优点，但是由于其存在着自身无法克服的缺点——稳态误差，因此，在对于精度要求相对严格的场合，就需要另外融入一些相应的方法来改善，甚至消除其稳态误差。积分模糊控制器就是在常规模糊控制器的基础上，融入了积分的环节。积分模糊控制器基本结构如图3所示。

图3 含有积分环节模糊控制器的结构

图中各个参数的意义如下：r，y分别为系统的设定值和系统的输出值(精确量)；e，ec，u分别为系统误差、误差变化率和模糊控制器的控制输出(精确量)；E，EC，U分别为系统误差、误差变化率和模糊控制器输出(模糊量)；Kec，Kc，Ku分别为误差、误差变化率的量化因子和控制量的比例因子；e0为给定误差值，即阈值(由用户根据系统的实际情况确定)；KI为积分系数(根据系统的实际情况确定)。

图3中控制器是由常规模糊控制模块、积分模块和判断模块组成，其控制原理是在系统进入稳态前，常规模糊控制器发挥作用，对系统进行控制使之快速响应，使系统输出迅速接近期望值。大误差在常规模糊控制器里是可以被很好地控制的；随着控制误差的减小，进入模糊控制论域中的零域时，模糊控制失去作用，此时系统会自动将积分环节加入其中，使小的误差继续累加，从而再次进入模糊控制的其他邻域，使模糊控制继续起作用。

假设e为模糊控制器的误差输入，则其输入的等价形式为

u1(t)=e1(t),t> 0.

(2)

引入积分环节后，模糊控制器的误差输入的等价形式变为

(3)

在式(3)中，t1为系统刚刚进入到小误差时刻(此小误差值也称为阈值，可根据现场的实际需求情况由用户自行设定)，t2为系统最终进入到稳态状态的时刻。

3 控制系统仿真与分析

3.1 适应性验证

为了验证此控制方法的性能，在航速分别为1 m/s和3 m/s下,对常规模糊控制、PID控制和积分模糊控制3种控制方法进行仿真，仿真结果如图4、图5所示。

图4 航速为1 m/s时的控制结果

图5 航速为3 m/s时的控制结果

由图4、图5可以看出，尽管航速有所改变，但3种控制算法中，不论是响应速度、超调还是稳态时间都是积分模糊控制为最优，且在不同的航速下，控制效果依然保持良好，随着航速的改变，控制性能保持良好。

3.2 抗干扰性验证

以一定程度的系统白噪声作为干扰源，分别在30 s时加入控制系统，同样对比航速为1 m/s和3 m/s时的控制结果，结果如图6、图7所示，从图中再次看出积分模糊控制效果仍然为最优。

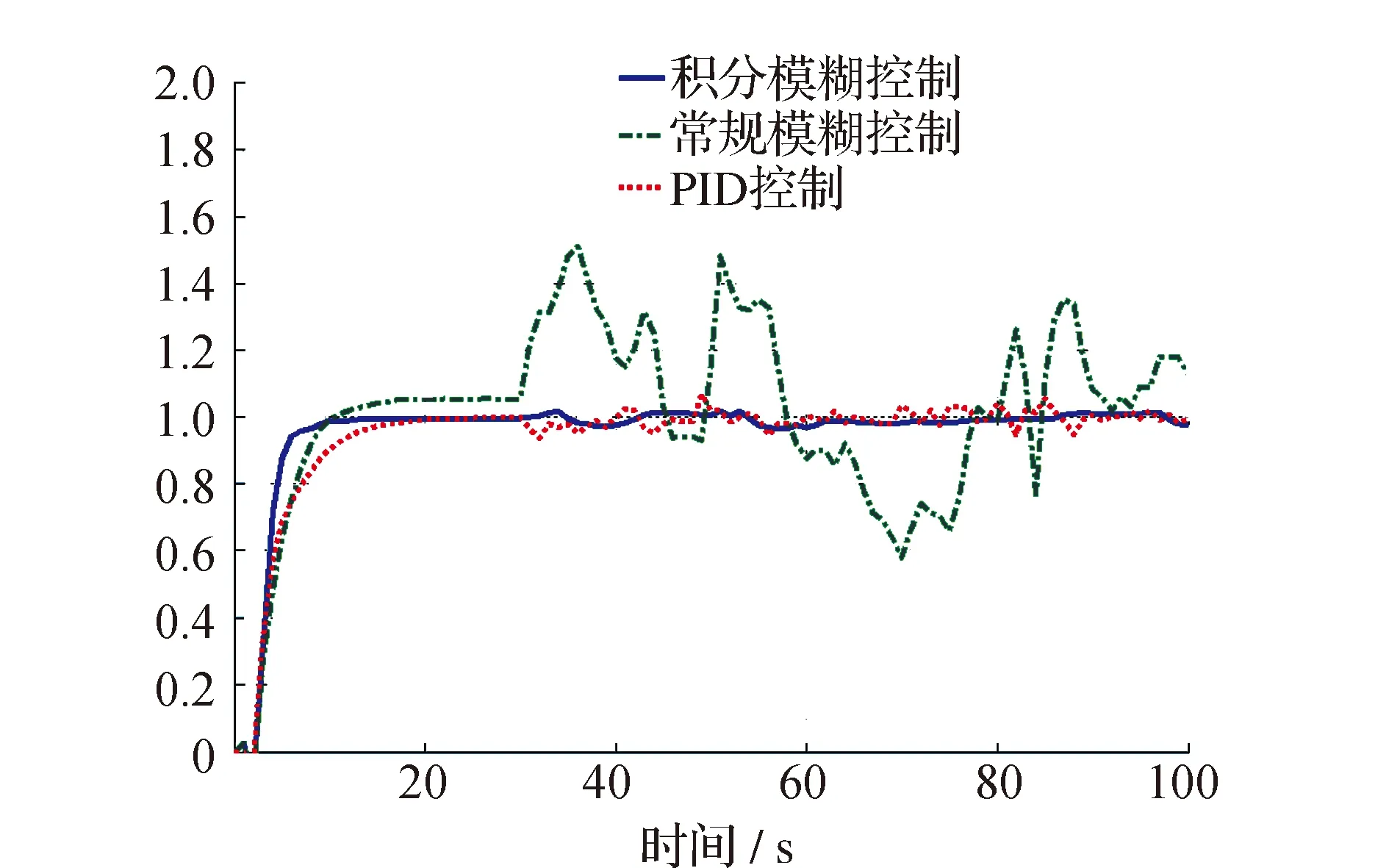
图6 航速为1 m/s时加入干扰的控制结果

图7 航速为3 m/s时加入干扰的控制结果

3.3 现场模拟实验

在模拟现场的实验中，加入偏离15°的指令，则控制效果如图8所示。

图8 模拟现场实验结果

在图8中，常规模糊控制稳态误差仍然存在，PID控制效果可以接受，但是各项指标最优的仍然是积分模糊控制。

4 结束语

本文通过建立AUV系统的控制模型，分析了系统存在的不确定性和扰动性，提出了带有积分环节的模糊控制方案，并在不同的航速下，以有、无干扰及不同的航速的情况下进行仿真，同时模拟实际的状况进行实验，仿真和实验的结果均表明：带有积分环节的模糊控制使系统的响应速度、稳定性和控制精度得到了明显的改善，并具有较好的鲁棒性。

[1] 万磊. 复杂环境下欠驱动智能水下机器人定深跟踪控制[J]. 上海交通大学学报, 2015,(49)12：1849-1854.

[2] 王芳,万磊，李晔，等. 欠驱动AUV的运动控制技术综述[J] . 中国造船, 2010,(21)2:227-238.

[3] 白龙，黄志峰，戈新生，等. 基于李群的水下航体动力学建模及最优控制[J]. 系统仿真学报, 2016, (28)5:1150-1157.

[4] 李娟，边信黔，熊华胜，等. AUV的精确航迹跟踪系统的鲁棒控制[J] . 哈尔滨工业大学学报, 2013,(45)1:112-117.

[5] 龚浩，吴先用，黄宇，等. 一种矢量推进方式下的AUV数学建模[J] . 中国仪器仪表, 2015，8:41-44.

[6] 郑荣，马艳彤，张斌，等. 基于垂向推进方式的AUV低速近底稳定航行[J] . 机器人, 2016,(38)5:588-592.

[7] 马利民. 欠驱动AUV全局无抖震滑膜轨迹跟踪控制[J]. 智能系统学报, 2016,(11)2:200-207.

[8] 姜言清. 约束条件下欠驱动AUV的路径规划研究问题研究[D]. 哈尔滨：哈尔滨工程大学, 2012.

[9] 袁健. 欠驱动式水下监测机器人航路点轨迹跟踪控制技术研究[J]. 科学管理报,2016,(36)1:38-47.

[10] 魏延辉，田海宝，杜振振，等. 微小型自主式水下机器人系统设计及试验[J]. 哈尔滨工程大学学报, 2014,(35)5:566-579.

[责任编辑：郝丽英]

The fuzzy control of the heading of an autonomous underwater vehicle without cables

YU Haoyang，LI Puqiang

(College of Electronic and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China)

An approximate mathematical model of heading control is established about the autonomous underwater vehicle. A fuzzy controller with integral links is designed, and the control mechanism of the fuzzy controller is analyzed. The basic structure of the integral fuzzy controller is given, and the simulation is carried out under the MATLAB /SIMULINK environment in this paper. Aiming at the mutual coupling between the degrees of freedom of autonomous underwater vehicles which the underwater movement is easily disturbed by many external environments, the motion is strongly nonlinear, and the heading control is unstable. The simulation results show that this control method can effectively improve the control performance of the control system, and has better robustness.

without cable; autonomous underwater vehicle；heading; fuzzy control；simulation

TP18

A

1671-4679(2017)05-0033-04

2017-07-04

于浩洋(1968-),男，副教授，研究方向：智能控制及仿真.

10.19352/j.cnki.issn1671-4679.2017.05.007