基于空间电压矢量的开关磁阻电机直接转矩控制
高旭东,杨春光,冷 爽
(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)
基于空间电压矢量的开关磁阻电机直接转矩控制
高旭东,杨春光,冷 爽
(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)
针对开关磁阻电机(SRM)转矩脉动抑制进行研究。首先,以1台3 kW、三相、12/8极SRM为样机, 利用二维有限元进行分析计算,在获取静态特性基础上,完成SRM样机的非线性建模。其次,针对SRM直接转矩控制(DTC),提出一种改进型SRM直接转矩控制策略,通过在换相区间合理地增加空间电压矢量,有效地改善转矩失控现象。最后,分别针对基本型DTC、传统CCC方式、改进型DTC,借助Matlab Simulink平台完成仿真分析。对比结果证实提出的改进型DTC策略对SRM转矩脉动抑制的有效性与优越性。
开关磁阻电机;转矩脉动;静态特性;非线性建模;直接转矩控制
开关磁阻电机(Switched Reluctance Motor,SRM)属于双凸极型变磁阻电机,其定、转子凸极均由具有高导磁率的硅钢片叠压而成,转子既无绕组也无永磁体,定子极上绕有集中绕组,通过定子上的集中绕组进行励磁。
开关磁阻电机调速系统(Switched Reluctance Drive,SRD)具有许多突出特点,主要包括:电机结构简单、坚固耐用,可工作于高速、超高速运转;其转子无绕组,损耗主要产生在定子,因而电机易于冷却处理;转子无永磁体,可允许有较高的温升;转矩方向与电流方向无关,从而可最大限度地简化功率变换器结构,降低系统成本;功率变换器不会出现直通故障,因而可靠性高;电机可以缺相运行,容错能力强;起动转矩大,低速性能好,无感应电动机在起动时所出现的冲击电流现象;调速范围宽,控制灵活,易于实现各种特殊要求的转矩-速度特性;在较宽的转速和功率范围内都具有较高效率;能够实现四象限运行,具有较强的再生制动能力。
尽管具有上述诸多优点,但较为明显的转矩脉动成为其最显著的缺陷,因此,限制了SRM在某些特殊场合的应用,如何有效地抑制SRM转矩脉动,已经成为SRM研究的热点之一。
当前,用于SRM转矩脉动抑制的方案主要有两种:其一为本体结构优化设计,其二为采取先进的控制策略。
在SRM本体结构优化方面[1-2],主要考虑尽量减小不对齐位置时各相绕组的最小电感;减小各相绕组之间的互感;降低各相绕组的开关频率等。
在控制策略方面,主要包括传统控制策略[3-4]、变结构控制[5-7]、智能控制[8-10]、转矩分配控制[11-12]、直接转矩控制[13-16]等策略。
本文通过对SRM样机进行有限元分析计算,获取静态特性,完成SRM非线性建模;提出一种改进型DTC策略,旨在改善转矩失控现象;借助Matlab Simulink平台,分别针对基本型DTC、传统CCC方式、改进型DTC完成仿真分析。最终证实了该改进型DTC策略的有效性。
1 SRM基本原理及其方程
1.1 SRM基本原理
SRM是一种磁阻可变电机,定、转子的结构均采用普通硅钢片叠压成的凸极形式,其工作遵循“磁阻最小原理”,其磁阻随着转子位置的变化而变化。
本文选用1台三相12/8极SRM样机作为研究对象,其步进角为15°,每转需24个步距,转子极距角为45°。其典型原理如图1所示。
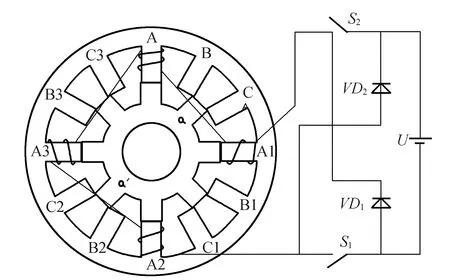
图1 三相12/8极SRM典型原理(单相)
以B相为例:当转子处于图1所示位置时,给B相通电,B相磁极励磁产生的磁场力使转子逆时针转动,直到轴线α-α′与定子极轴线B-B2对齐。此时,关断B相,接通C相,B相电流通过VD1和VD2续流,转子极向C-C2逼近。
若导通顺序按B→C→A→B,则转子转向为逆时针;若按B→A→C→B,则转子转向为顺时针。可见,转子转向是由各相绕组的通电顺序决定的。
三相绕组轮流通电,使得磁场旋转过一周,即转子转过一个极距角。当S1,S2接通时,电源U向绕组提供电能;当S1,S2断开时,电流利用二极管VD1,VD2续流,将储存的磁场能回馈给电源。
1.2 SRM基本方程
SRM满足基本电磁定律和能量守恒定律,可用电路方程、机械运动方程、机电联系方程予以描述,如下所示。
1)电压方程。经电路分析可得第k相的电压平衡方程表达式
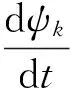
(1)
式中:uk为第k相端电压,ik为第k相电流,Rk为第k相电阻,ψk为第k相磁链。
2)磁链方程。由于SRM各相内部之间的互感远小于自感,故可将之忽略,可得其磁链方程为
ψk=Lk(θk,ik)ik.
(2)
式中:Lk为第k相绕组电感,θk为转子位置角度,ik为第k相绕组电流。
将式(2)代入式(1)可得:
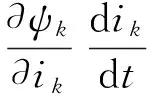
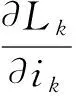
(3)
由式(3)可知:各相电压可由各相绕组电阻压降、电流变化引起磁链变化而感应产生的电动势、转子位置改变引起磁链变化而感应产生的电动势三部分组成。
3)机械运动方程。转子的机械运动方程式为
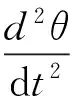
(4)
式中:Te为输出转矩,J为电机转动惯量,Kω为阻尼系数,TL为负载转矩。
4)机电联系方程。电磁转矩可以通过磁共能或磁场储能对转子位置角的偏导数求得。
(5)
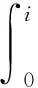
2 SRM非线性建模
本文利用Ansoft Maxwell 2D软件,对SRM的磁场分布以及磁链、转矩、电感等静态特性进行分析,获取其静态特性曲线。
本文选取的三相SRM样机主要结构参数为:定子外径: 120 mm; 转子外径: 73.2 mm; 定子内径: 72 mm; 转子内径: 30 mm; 定子轭厚: 10 mm; 转子轭厚: 10 mm; 定子极弧: 15°; 转子极弧: 16.95°。
如图2所示,由于SRM的结构是对称的,仿真时考虑的是0°~45°的转子极距角范围,故可将0°视为不对齐位置,22.5°视为对齐位置。
为保证模型精度,仿真过程中的步长值不宜取得过大,可取电流间隔为0.3 A,角度间隔为0.5°,得其静态特性曲线如图3所示。
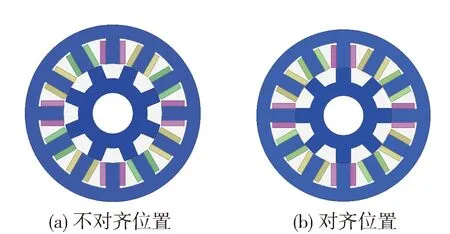
图2 三相12/8极SRM位置
由图3可知,磁链特性曲线ψj(θ,ij)是位置角θ及电流ij的非线性函数。θ为0°时,磁链线性度较好,随着位置角的增加,其磁路的饱和程度不断提高,非线性度逐渐增强。
利用所获电磁特性数据建立数据表,结合基本方程、运行和控制特性,建立SRM样机本体的非线性模型。SRM三相原理相同,各具独立性。以A相为例,由电路方程和有限元所得数据搭建的A相仿真模型如图4所示。
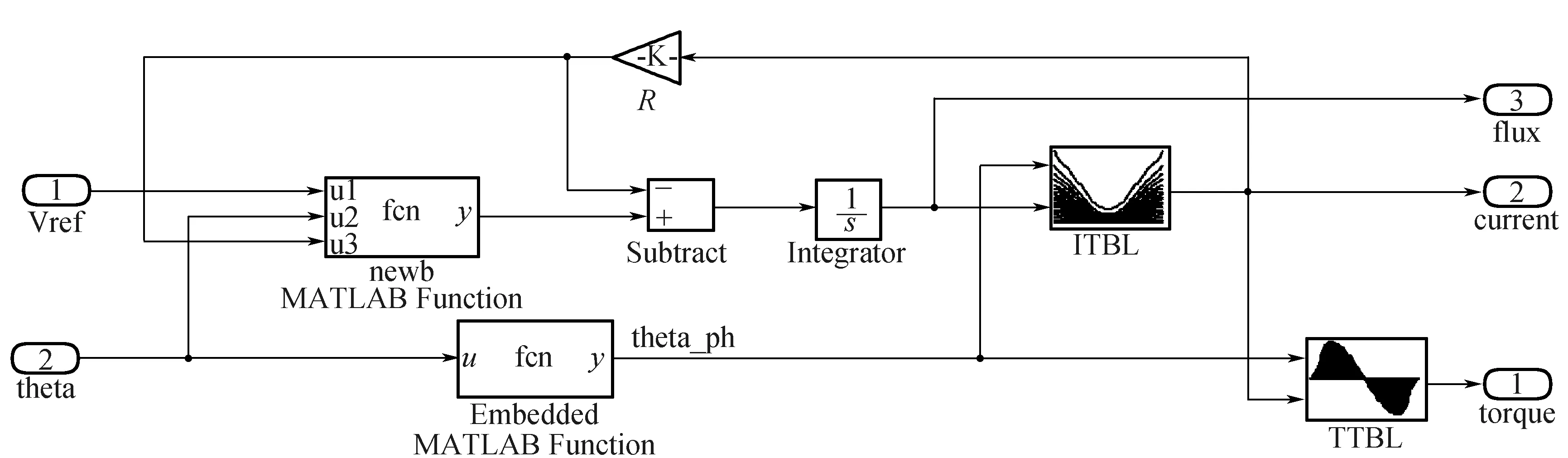
图4 A相仿真模型
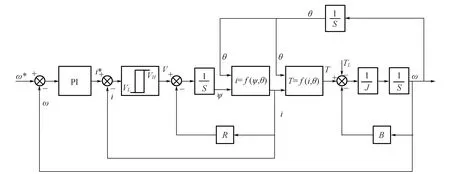
图5 SRD系统原理
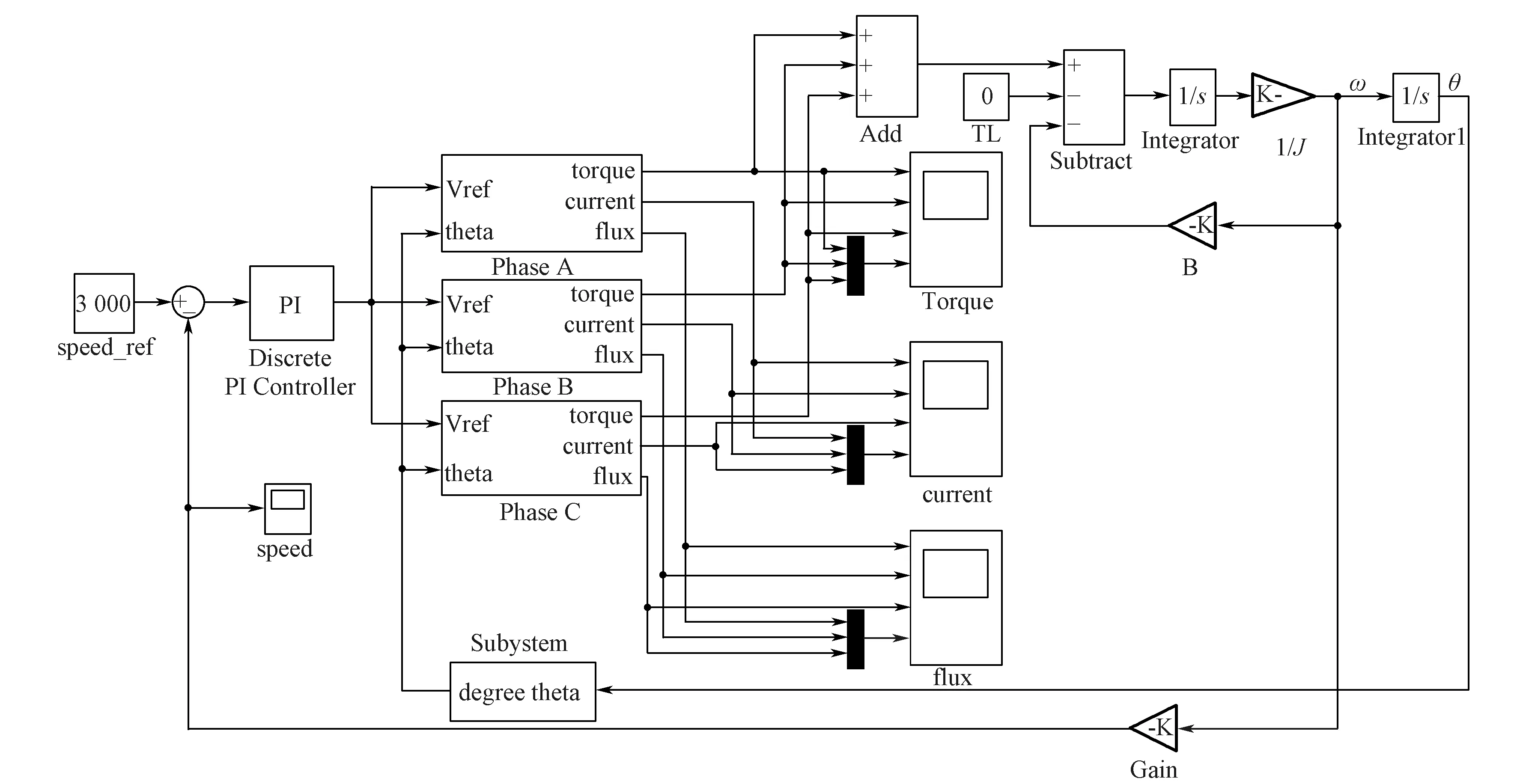
图6 SRD系统整体仿真模型
该SRD系统原理如图5所示。
SRD系统整体仿真模型如图6所示。
3 SRM直接转矩控制
直接转矩控制(DTC)是一种应用广泛而有效的转矩控制策略,其针对SRM进行转矩控制的核心思路为:将瞬时转矩和磁链估算后,与两者的给定值进行比较,将差值限定在滞环宽度内,再根据转矩、磁链的增减要求及磁链矢量所在扇区,查询开关表,选择要施加的电压矢量,控制开关管通断来驱动SRM换相转动。由此实现对转矩的直接控制,从而将转矩脉动限定在较小范围内。
经分析推导[15-16]可得SRM瞬时转矩表达式
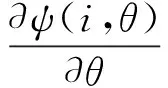
(6)
最终可得
ψ(k+1)=ψ(k)+U(k)Ts.
(7)
式中:U(k)为当前电压矢量;ψ(k),ψ(k+1)分别为当前和下个周期的磁链矢量,Ts为开关周期。如图7所示,通过改变电压矢量的幅值、方向及作用时间,就可以调节磁链矢量。
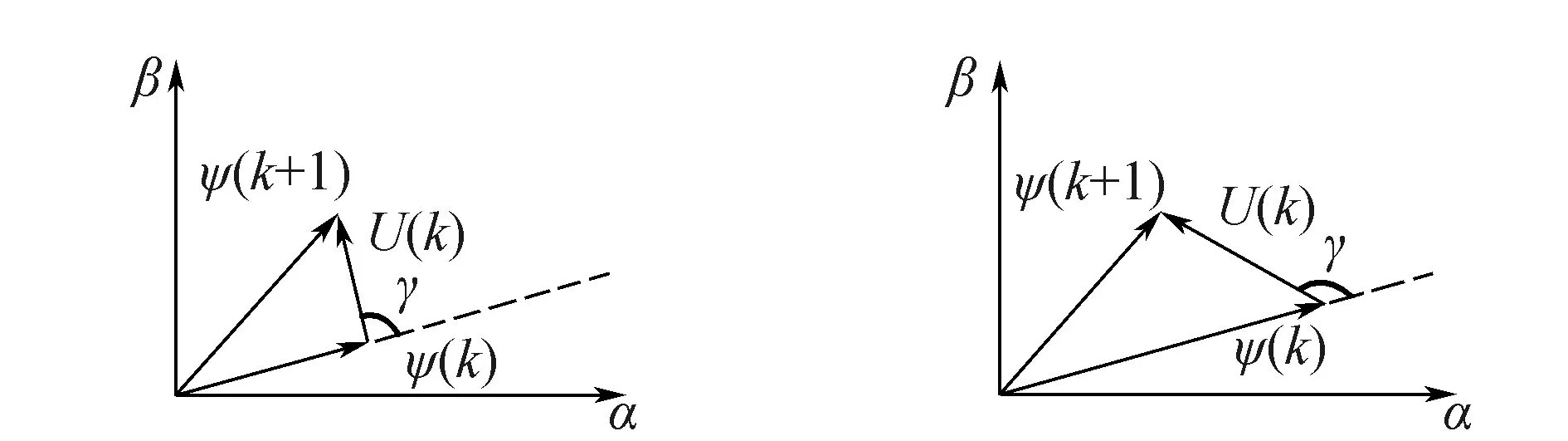
图7 磁链矢量与电压矢量
经分析可知:采用不同的电压矢量,会使磁链矢量幅值发生相应变化,磁链对转矩的控制可转化为电压矢量对转矩的控制。选择合适的电压矢量是实现SRM直接转矩控制的关键。
3.1 基本型DTC
3.1.1 基本空间电压矢量
本文采用常用的不对称半桥式结构功率变换器,该结构中各相相互独立。每相绕组的工作状态根据所加电压的不同均分为三种:“1”状态:2个开关管均导通,绕组承受正向电压;“0”状态:两个开关管中1只导通,1只关断,绕组电压为0,处于续流状态,若原来有电流,电流将自然下降,速度较慢,对转矩脉动抑制有利;“-1”状态:2个开关管均关断,绕组中仍有电流,承受负电压。该3种状态如图8所示。
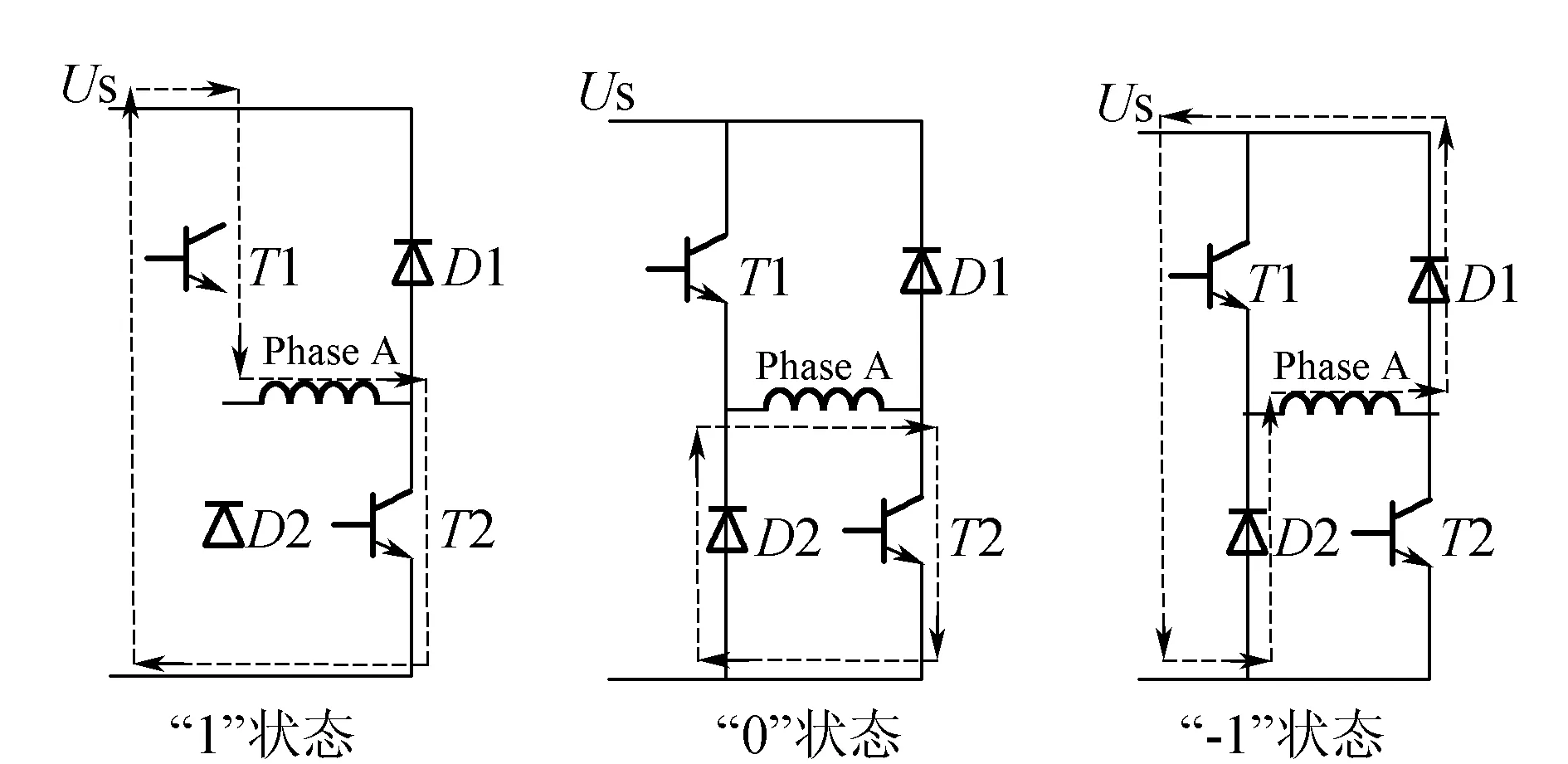
图8 不对称半桥结构3种工作状态
不难得知,三相SRM共有33=27种工作状态。考虑SRM实际运行情况,其基本空间电压矢量可选为如图9所示的幅值相等、空间角度互差60°的6个电压矢量V1~V6。
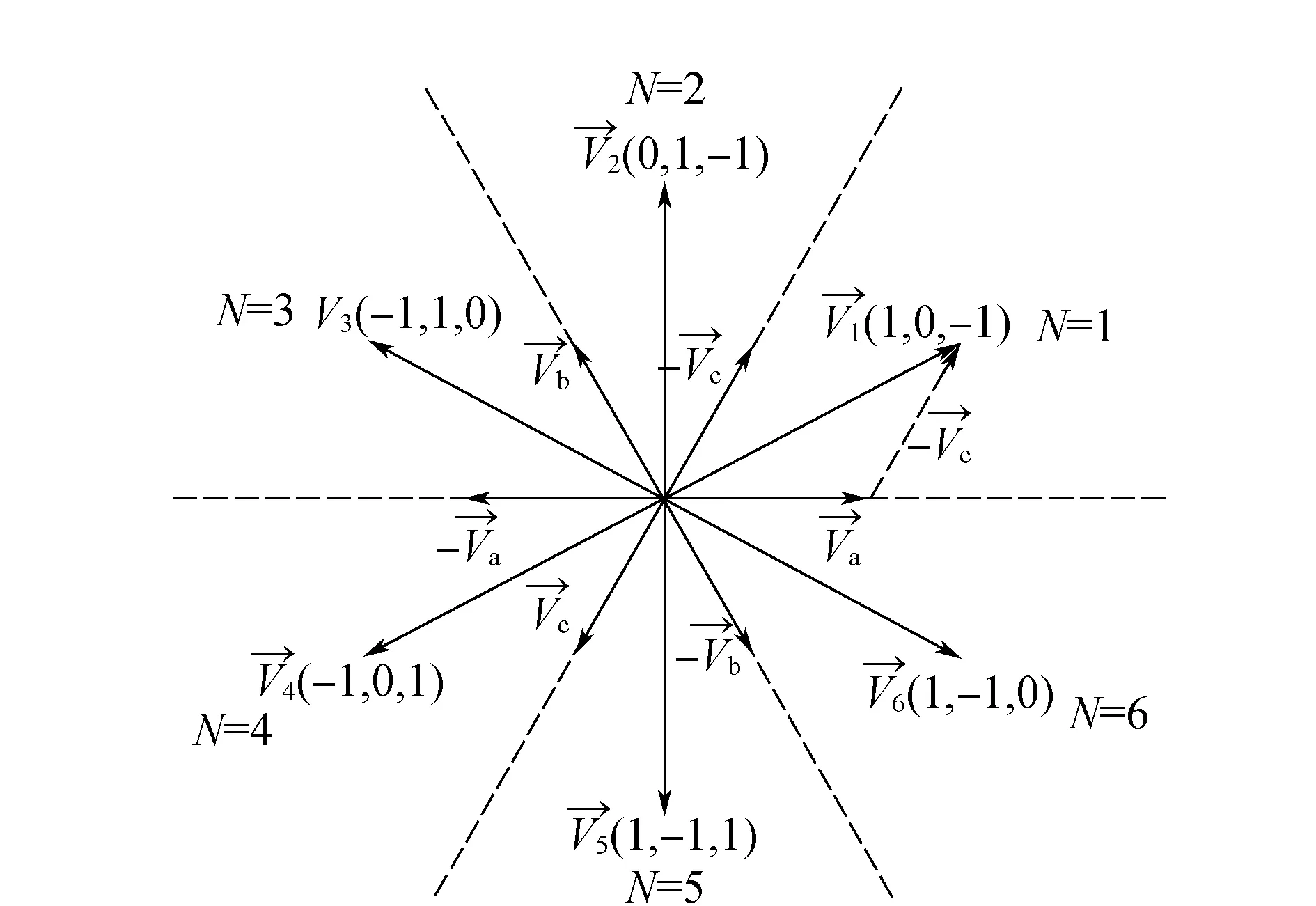
图9 三相SRM基本空间电压矢量
为表达方便,使用图8中的1,0,-1来表示各矢量。例如:V1=Va-Vc=1×Va+0×Vb+(-1)×Vc表示A相导通、B相续流、C相关断,即:(1,0,-1) 代表V1,V2~V6的描述与V1类似。矢量空间被分为6个均匀分布的扇区,用N=1,…,6表示。V1~V6分别位于各扇区的角平分线上。最终可得V1(1,0,-1)、V2(0,1,-1)、V3(-1,1,0)、V4(-1,0,1)、V5(0,-1,1)、V6(1,-1,0)。在整个控制过程中,相邻矢量间按照“1→0→-1”的顺序或逆序变换原则,要求绕组电压从正压要先经过零压才到负压,反之亦然,从而避免了各相较大的电压跃变,有利于减小换相时的转矩脉动。
3.1.2 电压矢量开关表
以SRM逆时针转动情况进行分析,当某时刻磁链矢量位于扇区N=1,经分析可知:要增大磁链的幅值,应选取V2或V6;要减小磁链的幅值,应选择V3或V5;如果要增大转矩,可以选取在旋转方向上超前于定子磁链的电压矢量,即V2或V3;如果要减小转矩,则选取滞后于定子磁链的电压矢量,即V5或V6。可针对6个扇区予以分析,以k来表示扇区号,则有:若需增大磁链矢量幅值则选取Vk+1或Vk-1;若需减小磁链矢量幅值则选取Vk+2或Vk-2;若需增大转矩幅值则选取Vk+1或Vk+2;需减小转矩幅值选取Vk-1或Vk-2。
经分析推导可得基本型DTC磁链滞环控制过程如图10所示。
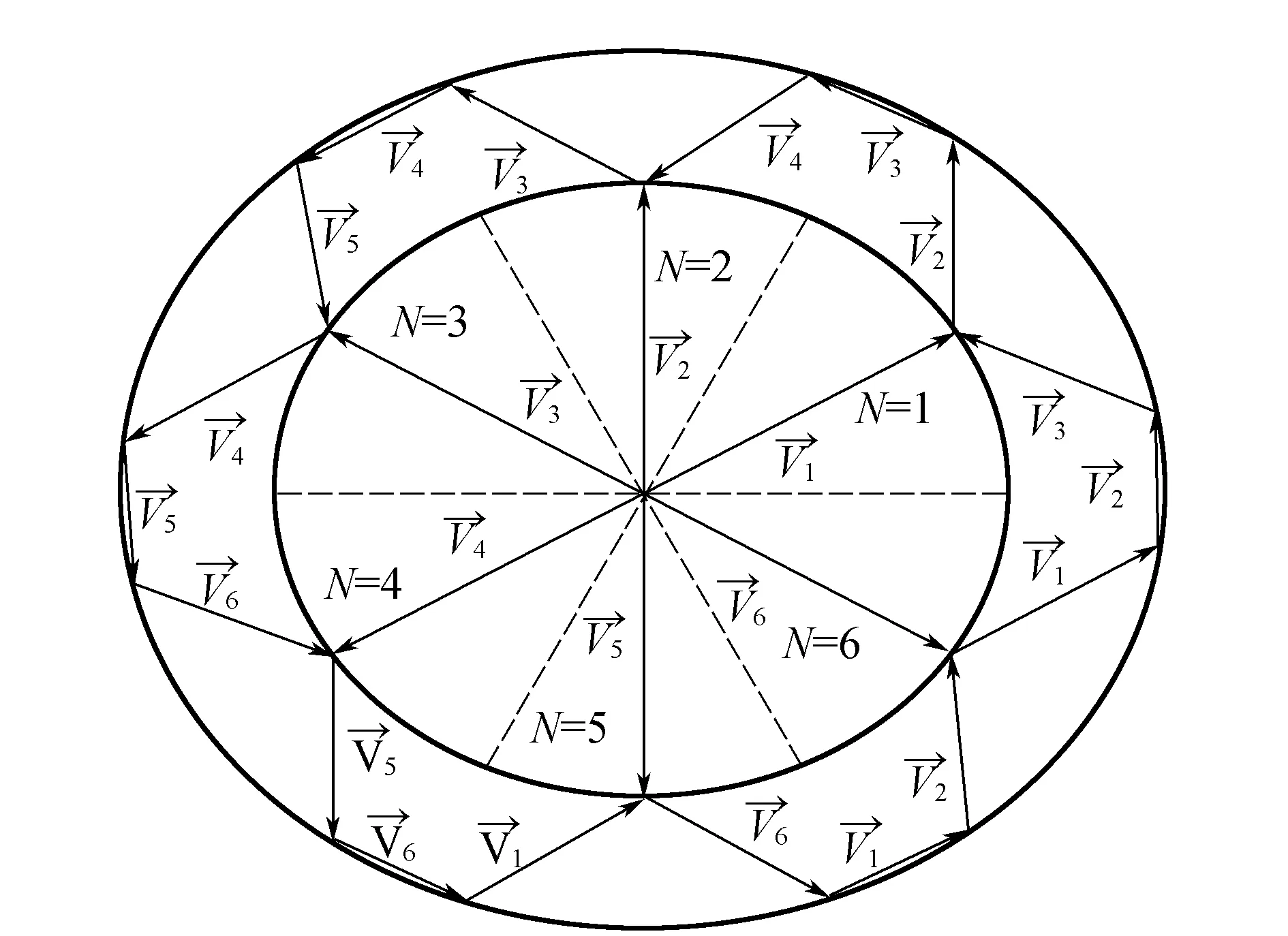
图10 基本型DTC磁链滞环控制
综上可得SRM的电压矢量开关表如表1所示。
符号↑和↓分别表示需要增大和需要减小。不同的电压矢量,对应控制打开和关断相应的开关管。

表1 电压矢量开关
由表1可得完整的三相SRM的基本型DTC开关表。 控制器据此对功率变换器发出控制指令以调节转矩与磁链。
3.2 改进型DTC
上述基本型DTC在某些情况下会产生转矩失控现象,由此导致系统不稳定。经分析可知:该转矩失控现象主要就是发生在换相区附近。当换相时,换相区内前一相转矩的减小量比后一相转矩的增加量要大,导致总输出转矩的值比其它位置小,使得换相区不能满足转矩和磁链均需增大时的要求。
以B相和C相的换相区为例:当转矩和磁链均需增大时,换相区内应从V3(-1,1,0)转换到V4(-1,0,1),V4对转矩的作用效果是:A相不变、B相减小、C相增大,而B相转矩的减小量比C相转矩的增加量大,使得该区域内合成瞬时转矩总体是减小的,不能满足转矩控制要求,从而产生转矩失控现象,使换相区的转矩脉动明显。
针对基本型DTC存在的转矩失控缺点,本文提出改进型DTC以消除转矩失控现象,进而提高SRD转矩性能。
3.2.1 空间电压矢量改进
如图11所示,在每个换相区位置增加一个改进的电压矢量。三相SRM共需添加3个改进电压矢量V1+(1,1,-1)、V3+(-1,1,1)和V5+(1,-1,1)。
以B相和C相的换相区为例:当转矩和磁链均需增大时,换相区内从V3(-1,1,0)转换到V4(-1,0,1),则A相状态不变,B相关断,C相导通。令B相和C相在这段区间内均导通,以使导通相数增加,即有(-1)×Va+1×Vb+1×Vc,用V3+(-1,1,1)表示。增加空间电压矢量V3+后,换相区内从V3(-1,1,0)转换到V3+(-1,1,1),使C相绕组提前开通,在该时刻B相和C相同时导通,最终使得A相转矩缓慢减小、B相转矩不变、C相转矩快速增大,则其合成转矩增大,由此满足对转矩和磁链的要求。
同理,在C相与A相的换相区,使A相提前开通,即增加V5+(1,-1,1);在A相与B相的换相区,使B相提前开通,即增加V1+(1,1,-1)。
当需转矩与磁链均上升时,SRM按照A→A+B→B→B+C→C→C+A→A次序运行, 此时在换相区采用改进型电压矢量控制开关管,从而有效地消除转矩失控现象。
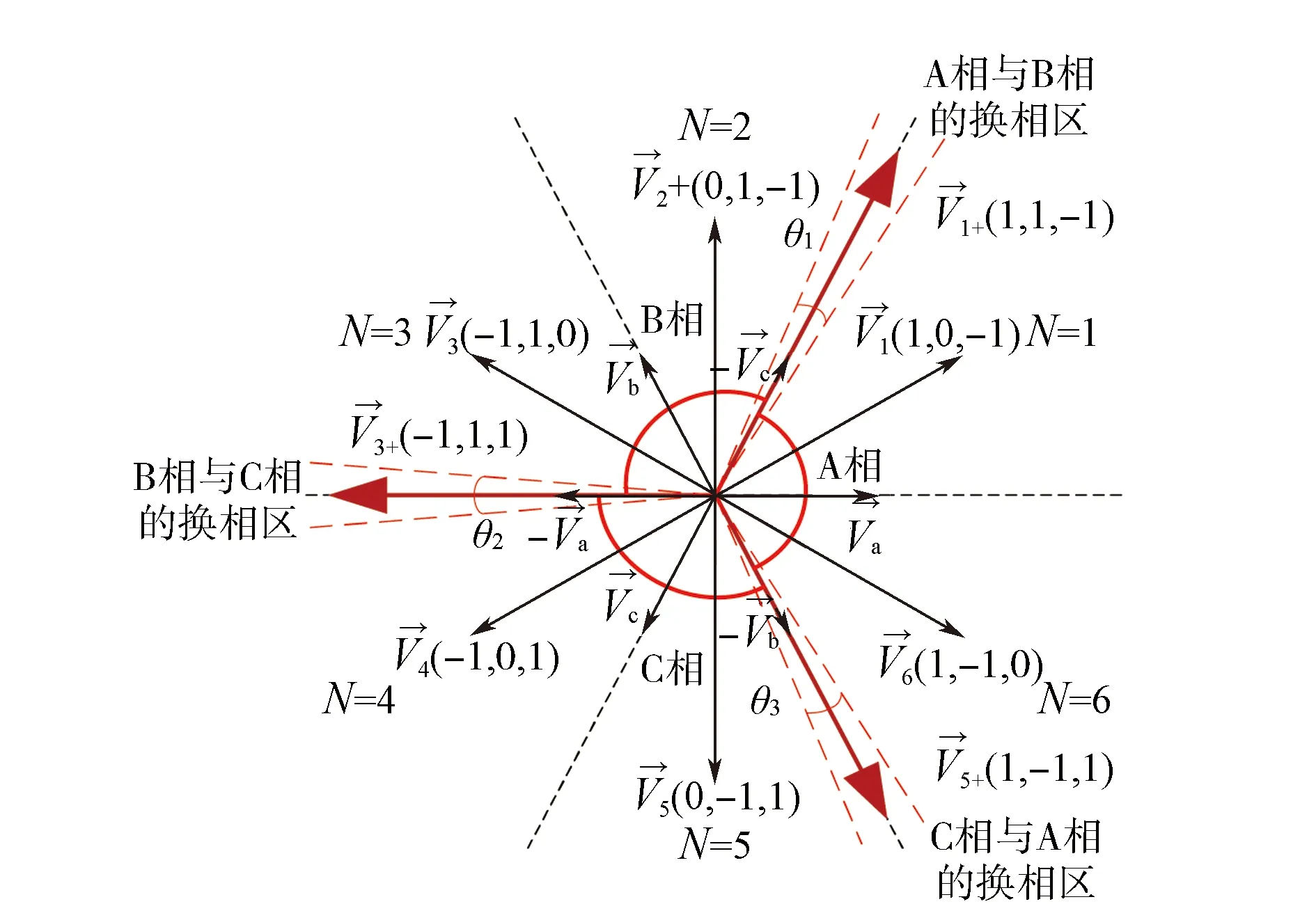
图11 基于换相区的空间电压矢量
3.2.2 改进型DTC实现方式
改进型DTC方法在换相区内,利用换相区空间电压矢量来代替先前的基本电压矢量,V1+(1,1,-1)、V3+(-1,1,1)和V5+(1,-1,1)分别将B相、C相、A相提前开通。其换相过程如图12所示。
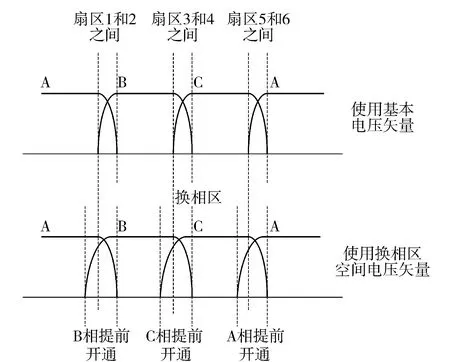
图12 三相绕组换相过程
换相区的大小由SRM本身性质、检测装置精度和控制器运算速度等确定。同时,换相区的意思就是下一相往前提了一个角度,实际上,上一相还处在电感的下降区,会产生负转矩,而下一相提前产生正转矩,正负转矩的共同效果使得提前的这个角度里三相总转矩值基本不变。
当系统中产生的滞环控制指令表明转矩和磁链的幅值均需增大时,采用原有的6个基本电压矢量加上增加的3个换相区电压矢量,共同控制开关管的通断,这样会使原来转矩失控区域合成的总电磁转矩增大,使控制效果满足系统要求;当幅值变化要求是均需增大以外的其他情况时,仍采用基本电压矢量即可。
4 仿真结果
为检验本文研究成果,分别将改进型DTC与基本型DTC、传统CCC方式的转矩控制效果进行对比并加以分析。
4.1 改进型DTC与基本型DTC对比
图13所示为SRD采用基本型DTC仿真波形。
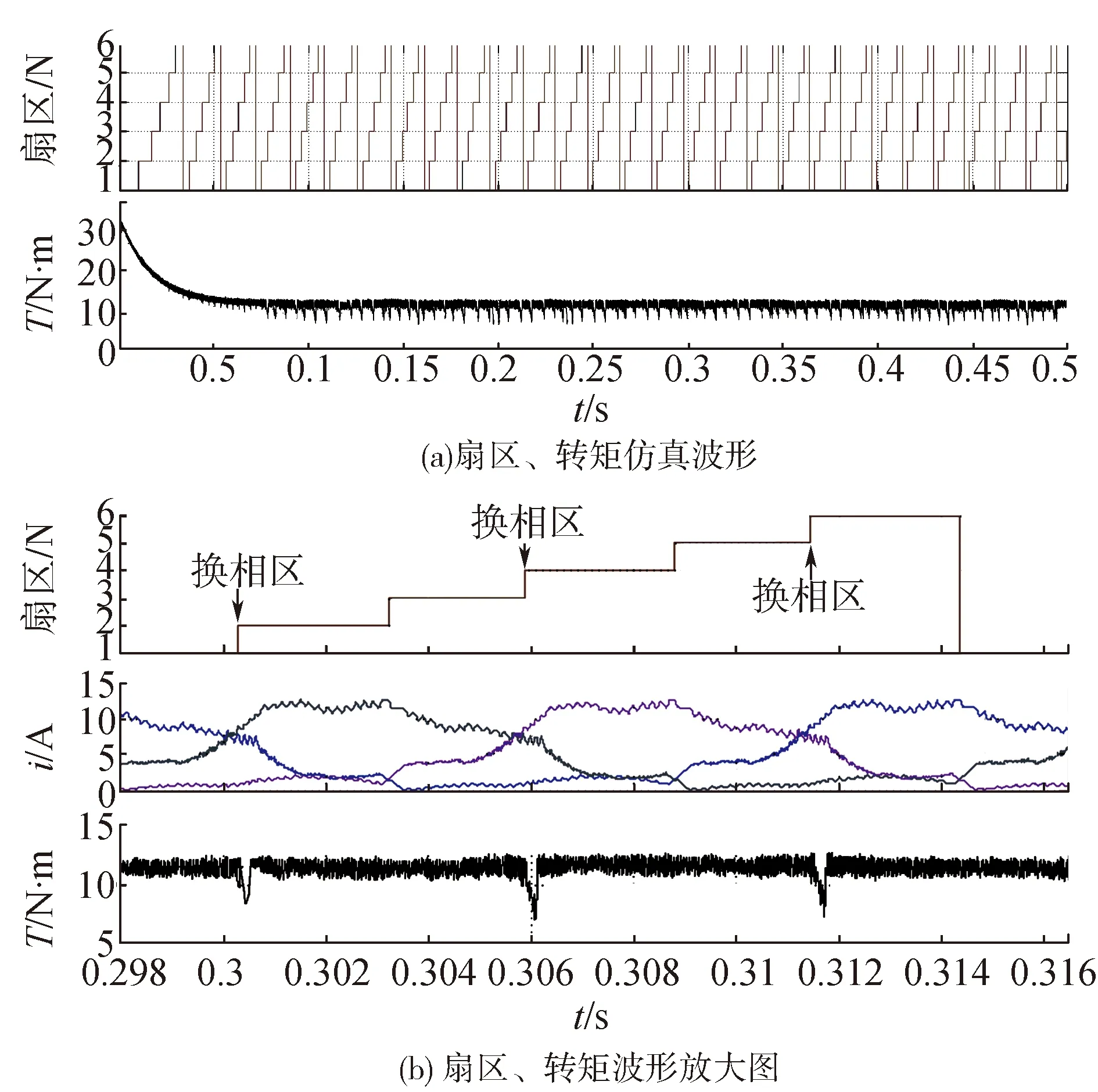
图13 采用基本型DTC仿真波形
可以看出,基本型DTC策略下的转矩脉动较大,在换相期间的转矩明显小于正常值,即存在转矩失控现象。
图14所示为SRD采用改进型DTC仿真波形。
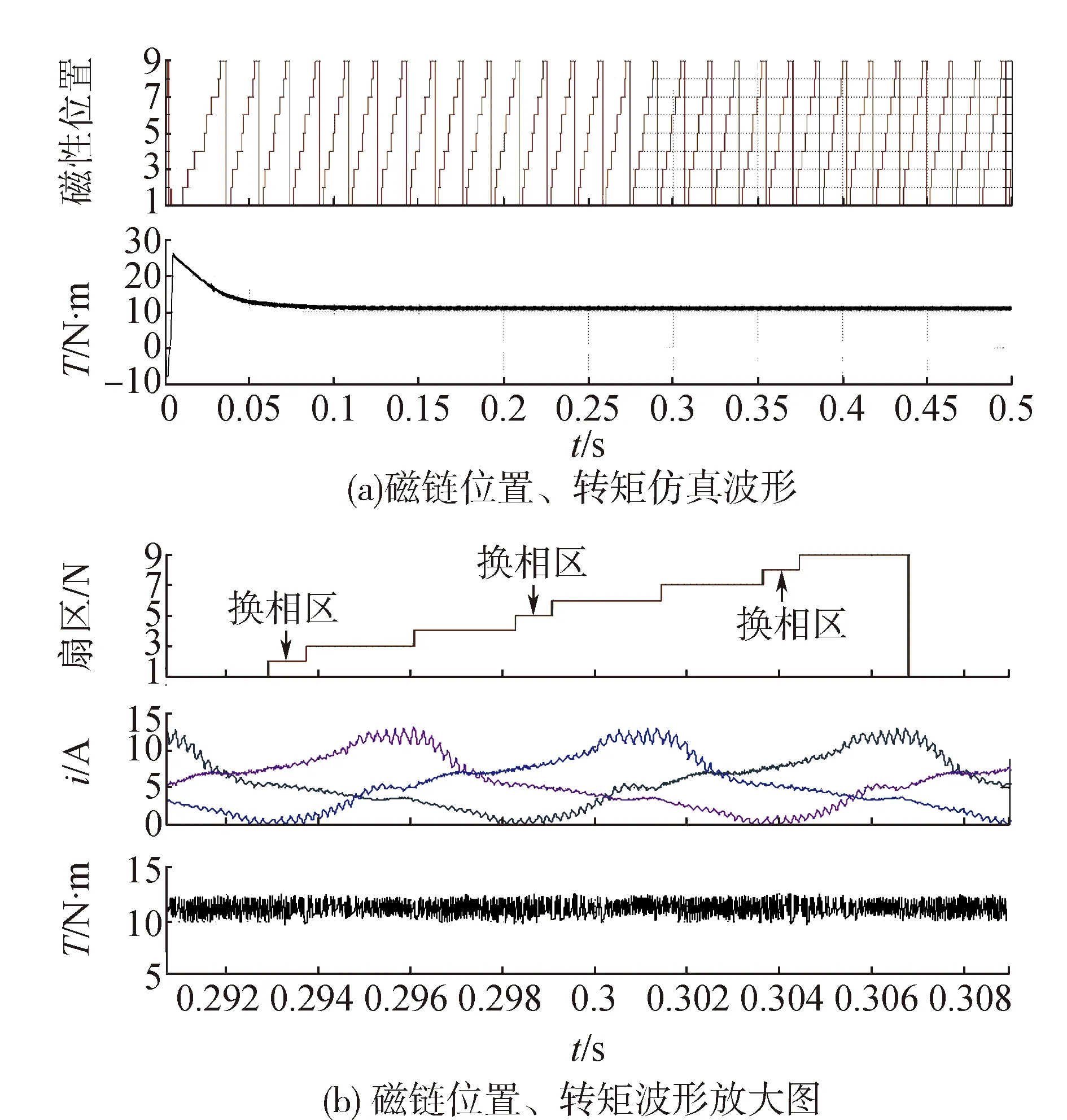
图14 采用改进电压矢量时的仿真波形
经对比可知:改进型DTC下的SRM转矩控制,基本消除了转矩失控现象,转矩脉动也明显减小且其电流过渡区变宽,换相区位置的转矩变得平稳。
4.2 改进型DTC与传统CCC方式对比
在负载10 N·m、转速500 r/min、给定磁链0.4 Wb条件下,改进型DTC的仿真波形如图15所示。
图15中从上至下依次为扇区、磁链、电流、转矩波形。
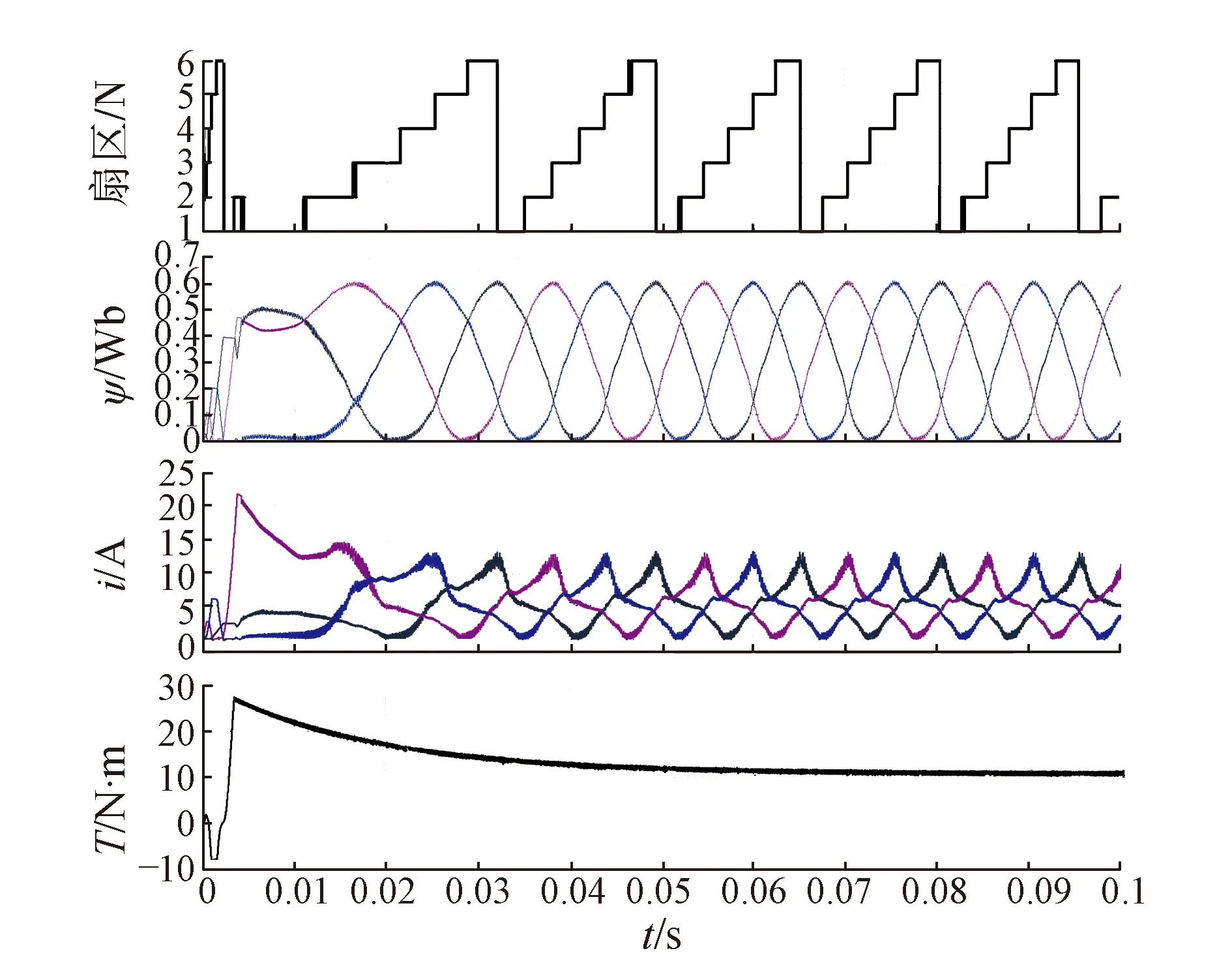
图15 改进DTC的仿真波形
图16所示为采用传统CCC方式仿真波形。
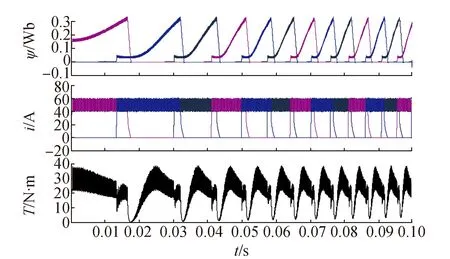
图16 传统CCC方式的仿真波形
由以上可知:采用改进型DTC,其启动转矩脉动更小,转矩密度高于CCC方式,其根本原因在于改进型DTC下的SRM在一个转子极距角内均工作,绕组利用率较高,其转矩幅值较为稳定,脉动控制在较小范围内并且响应较快,而传统CCC方式下的转矩波动范围明显较大。
5 结束语
本文针对基本型DTC及其存在的转矩失控现象,在6个基本电压矢量的基础上,通过在换相区间增加3个电压矢量,提出了一种改进型DTC策略,从而使得基本型DTC转矩失控区域的转矩输出得以控制,有效地改善了转矩失控现象,提高了SRD转矩性能。借助Matlab Simulink平台,分别针对基本型DTC、改进型DTC及传统CCC方式3种情况进行仿真与分析,结果证实了本文提出的改进型DTC能够更好地实现SRM转矩控制。
[1] 宋受俊,葛乐飞,刘虎成,等.开关磁阻电机设计及多目标优化方法[J].电工技术学报,2014,29(5):197-204.
[2] 宋受俊,葛乐飞,蒋艳玲.基于文化粒子群算法的开关磁阻电机多目标优化设计[J].西北工业大学学报,2014,32(1):111-116.
[3] 吴红星. 开关磁阻电机系统理论与控制技术[M]. 北京: 中国电力出版社, 2010.
[4] 王宏华. 开关型磁阻电动机调速控制技术[M]. 2版.北京: 机械工业出版社, 2014.
[5] SHI Tingna, NIU Longtao, LI Wenshan. Torque-ripple minimization in switched reluctance motors using sliding mode variable structure control[C]. in 2010 29th Chinese Control Conference (CCC), 2010:332-337.
[6] MANOLAS I, PAPAFOTIOU G, MANIAS S N. Sliding mode PWM for effective current control in Switched Reluctance Machine drives[C]. in 2014 International Conference on Power Electronics Conference (IPEC-Hiroshima 2014 - ECCE-ASIA), 2014:1606-1612.
[7] BIZKEVELCI E, LEBLEBICIOGLU K, ERTAN H B.A sliding mode controller minimize to SRM torque ripple and noise[C]. in 2004 IEEE International Symposium on Industrial Electronics , 2014:1333-1338.
[8] MURUGAN M, JEYABHARATH R.Neuro Fuzzy Controller Based Direct Torque Control for SRM Drive[C]. in 2011 International Conference on Process Automation, Control and Computing (PACC), 2011:1-6.
[9] 夏长亮, 修杰. 基于RBF神经网络非线性预测模型的开关磁阻电机自适应PID控制[J]. 中国电机工程学报,2007, 27(3): 57-61.
[10] 夏长亮, 陈自然, 李斌. 基于RBF神经网络的开关磁阻电机瞬时转矩控制[J].中国电机工程学报, 2006, 26(19): 127-131.
[11] LEE Dong-Hee,LEE Zhen-Guo,AHN Jin-Woo.Instantaneous Torque Controlof SRM with a Logical TorqueSharing Method[C].in PESC 2007 Power Electronics Specialists Conference, 2007:1784-1789.
[12] LEE Dong-Hee, LIANG Jianing, LEE Zhen-Guo, et al. A Simple Nonlinear Logical Torque Sharing Function for Low-Torque Ripple SR Drive[C].in IEEE 2009 Transactions on Industrial Electronics, 2009:3021-3028.
[13] 王云刚,陈文燕. 一种改进的DTC策略在SRM上的应用[J].科学技术与工程, 2013(15): 4384-4388.
[14] 叶敏,曹秉刚. 四相开关磁阻电机直接转矩控制[J].微特电机,2010(5): 45-48.
[15] 许爱德,樊印海,李自强. 空间电压矢量下SRM 转矩脉动最小化[J].电机与控制学报, 2010(1): 35-40.
[16] 王子煜,邓福军. 基于模糊理论的开关磁阻电机直接转矩控制[J].大连交通大学学报, 2013(2):97-100.
Direct torque control of switched reluctance motor based on space voltage vector
GAO Xudong,YANG Chunguang,LENG Shuang
(College of Electrical and Information Engineering,Heilongjiang Institute of Technology,Harbin 150050, China)
Torque ripple suppression of switched reluctance motor(SRM) is studied in this paper. Firstly, a three-phase, 12/8 pole, 3kW SRM is selected as the prototype. Two-dimensional finite element is used to analyze and calculate the prototype of SRM. Based on the gained static characteristics, nonlinear modeling of SRM is completed. In view of direct torque control (DTC) of SRM, an improved DTC method is proposed, by adding some space voltage vectors in commutation interval reasonably, so the uncontrollable phenomenon of torque can be improved to some extent. In the end, respectively for basic DTC, conventional CCC and the improved DTC, the simulations and necessary analysis are completed inMatlabSimulinkplatform. The simulation result verifies the validity and superiority of the proposed DTC method for torque ripple suppression of SRM.
switched reluctance rotor; torque ripple; static characteristics; nonlinear modeling; DTC
[责任编辑:郝丽英]
TM352
A
1671-4679(2017)05-0026-07
2017-02-26
哈尔滨市科技局创新人才研究专项基金项目(RC2015QN007008)
高旭东(1973-),男,副教授,研究方向:电机智能控制;电力电子装置自动化.
10.19352/j.cnki.issn1671-4679.2017.05.006

