“分参”？“不分参”？——导数研究函数过程中的思考

潘志琴

(溧阳市戴埠高级中学,江苏 常州 213300)

“分参”？“不分参”？
——导数研究函数过程中的思考

潘志琴

(溧阳市戴埠高级中学,江苏 常州 213300)

“教无定法，学无止境”.在高中阶段导数的学习中，在参数范围的探究过程中，对“分参”与“不分参”的选择，教师的教与学生的学都很无奈.学生在无奈地选用导数研究含参函数最值过程中的苦与低效，面对这种情况，教师可以考虑引导学生从更多的实例中汲取经验.

参数分离；构建函数；分类讨论

导数是研究函数问题的工具，对于导数部分的复习主要放在利用导数研究函数的性质等内容上，特别是含参数问题是近些年来高考的重点和热点内容.此类问题通常涉及求最值和恒成立条件，要求学生在求解中重视分类讨论、数形结合、分离参数等基本思想方法的运用.

在这些思想方法中，若能先进行分离参数，后对函数进行无参操作，一般则能简化运算.例如：已知函数f(x)=alnx+x2(a为常数)，若存在x∈[1,e],使得f(x)≤(a+2)x成立，则实数a的取值范围是 .

解法1 ∃x∈[1,e],使得alnx+x2≤(a+2)x，

即∃x∈[1,e],使得a(x-lnx)≥x2-2x.

易证：x∈[1,e]时，x-lnx>0.

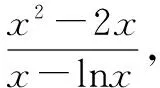
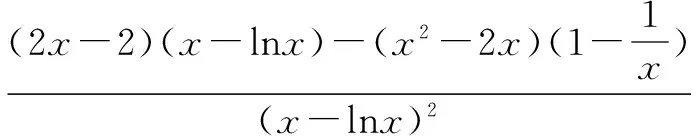
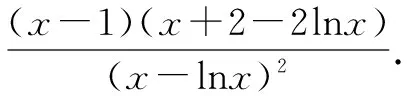
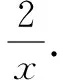
∴φ(x)≥φ(2)=4-2ln2>0.∴φ(x)在[1,e]上均大于0,∴h′(x)在[1,e]上恒大于等于0，∴h(x)在[1,e]上单调递增.

∴hmin=h(1)=-1，∴a≥-1.

解法2 不分参，分三类进行讨论.(过程略)

对于以上例题，还可以有两种解法进行比较：解法一可以避免分类讨论，相比解法二比较简洁；解法二给出了求函数最值的基本方法，由于是含有参数的函数求最值，所以必须分类讨论.在近些年的导数研究函数的过程中，在“分参”与“不分参”的问题上，有一些问题可能根本没有选择方法的机会，师生必须面临带参数求解最值.下面我们用具体例题来体会这种“无奈”.

2017年苏锡常一模第19题：已知函数f(x)=(x+1)lnx-ax+a(a为正实数，且为常数).

(1)若函数f(x)在区间(0,+)上单调递增，求实数a的取值范围；

(2)若不等式(x-1)f(x)≥0恒成立，求实数a的取值范围.

分析(2)(x-1)f(x)≥0恒成立

⟺①x=1时，易证；

②x>1时，(x+1)lnx-ax+a≥0且x∈(0,1)时，(x+1)lnx-ax+a≤0.

解∵∀x>0,(x-1)f(x)≥0，

∴①x=1时，a>0时均成立.

②x>1时，(x+1)lnx-ax+a≥0.

∴g(x)在(1,+)上单调递增,∴g(x)>g(1)=2.

当a∈(0,2]时，f′(x)恒大于0，∴f(x)在(1,+)上单调递增,∴f(x)>f(1)=0.

当a>2时，∃x0∈(1,+),使得f′(x0)=0.列表：

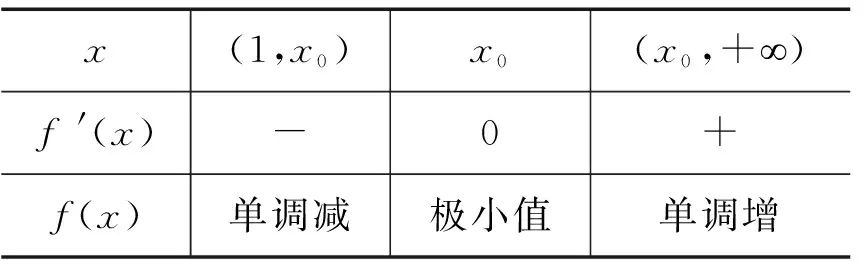
x(1,x0)x0(x0,+¥)f'(x)-0+f(x)单调减极小值单调增

∵f(1)=0， ∴当x∈(1,x0)时，f(x)<0.

③0

即证：∀x∈(0,1),(x+1)lnx-ax+a≤0.

∴f′(x)>f′(1)=2-a>0.

∴f(x)在(0,1)上单调递增，

∴f(x)

因此，0

以上两个例子之所以在貌似还可以进行“分参”的情况下依然直接研究带参数函数的最值，是因为真正分参时无法进行下去.

“分参”一般是需要条件的：①参数a可以方便地“分离”，达到用含“x”的不含参函数表示；②借助新函数的单调性可以得到所需要的最值.

在高中教学的实际过程中，笔者深切体会到学生在无奈地选用导数研究含参函数最值过程中的苦与低效，面对这种情况，教师可以考虑引导学生从更多的实例中汲取经验.

美国数学家波利亚说过：“好问题同某种蘑菇相似，它们都成堆地生长，找到一个以后，你应当在周围找一找，很可能附近就有好几个.”作为普通的高中教师，真正有助于学生的教学应该是基于学生，又能让学生在此基础上有提升的教学.让我们做个教育的有心人，引导学生在这个“蘑菇”的附近去亲近一堆“蘑菇”，抛开无奈，可以“分参“就分参，不可以”分参“就”“不分参.

[1]吴文前.高等数学与中学数学教学的衔接[J].教育与教学研究，2010(10).

[2]俞求是.高中新课标函数与微积分有关内容的处理研究[J].课程·教材·教法，2010(09).

[3]匡武俊.高中微积分教学策略[J].中国教育技术装备，2010(08).

G632

A

1008-0333(2017)22-0002-02

2017-06-01

潘志琴(1982.10-)，女，汉族，中学一级教师，大学本科，从事高中数学解题方法与策略研究.

责任编辑：杨惠民]