让“定义优先”的经验成为圆锥曲线中解题的利器

龙 耒 杨 莉

(湖北省宜昌市三峡高级中学，湖北 宜昌 443000)

让“定义优先”的经验成为圆锥曲线中解题的利器

龙 耒 杨 莉

(湖北省宜昌市三峡高级中学，湖北 宜昌 443000)

《普通高中数学课程标准(修订)》拟将提出数学基本活动经验，它将与基础知识、基本技能、基本数学思想一起构成高中数学的“四基”.在数学学习活动中，要使学生真正理解数学知识，感悟数学的理性精神，形成创新能力，就应该让学生积累丰富而有效的数学活动经验.而积累经验的目的就是为了更好地运用经验解决实际问题.学生在圆锥曲线的学习中形成的“定义优先”的经验，就应该成为圆锥曲线中解题的利器.

数学基本活动经验;定义优先

[文1]指出，所谓数学基本活动经验，是指在数学目标指引下，通过对具体事物进行实际操作、考察和思考，从感性向理性飞跃时所形成的认识.人教A版教材将圆锥曲线的统一定义作为阅读材料呈现给学生，显然新课标降低了对统一定义的要求，也大大降低了学习的难度，这样反而凸显了第一定义的重要性.本文所讲述的定义就是指圆锥曲线的第一定义.本文通过几个案例解决两个问题，一是如何让学生形成“定义优先”的数学基本活动经验；二是如何利用“定义优先”的经验来解题.

一、获得经验

人教A版2-2教材设计三个问题情境，通过具体的数学活动，分别得到椭圆、双曲线和抛物线的定义.在前两个问题情境中，学生可以通过动手操作，画出椭圆和双曲线.第三个问题情境学生运用几何画板画出抛物线.在这三个问题情境中，学生参与的就是数学基本活动.根据活动得到的结论就是椭圆、双曲线和抛物线的定义，这种体验一定会给学生留下深刻的印象.这就为后来在教师的引导下根据定义推导三种圆锥曲线的标准方程奠定了基础.

案例1 (人教A版2-2 P49 A组第1题)

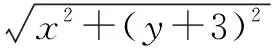
学生看到这个问题后，会自然地联想到用直接法求曲线的方程.于是，相当一部分学生会模仿求椭圆标准方程的化简过程，对原代数关系式进行变形和化简，从而得到点M的轨迹方程，进而根据方程判断出点M的轨迹是椭圆.当学生解决完这个问题后就会恍然大悟，自然会想起椭圆的定义.题目中的代数关系式可以转化为几何关系式：|MF1|+|MF2|=10>|F1F2|=6，学生此时会运用椭圆的定义直接得到动点的轨迹是椭圆，然后写出曲线的方程.

案例2 (人教A版2-2 P49 A组第7题)

如图，圆O的半径为定长r，A是圆O內一个定点，P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

案例3 (人教A版2-2 P62 A组第5题)

如图，圆O的半径为定长r，A是圆O外一个定点，P是圆上任意一点.线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

学生在完成这两个问题的过程中肯定会遇到困难，教师应该帮助学生从题目中线段的垂直平分线的性质入手，引导学生作出辅助线.

从而得到 |QO|+|QA|=|QO|+|QP|=r>|OA|.(案例2)

|QA|-|QO|=|QP|-|QO|=r<|OA| (案例3)

学生会根据这两个几何关系式，结合椭圆和双曲线的定义，得到点Q的轨迹分别是椭圆和双曲线.

学生随着对这些本质相同、情景多样的问题的解决，所获得的数学活动经验的数量也不断增加，并逐步摆脱圆锥曲线的具体活动情境，从中概括出这些具体活动情景所具有的共同本质特征：圆锥曲线的问题，要优先考虑定义，这样思考不仅能快速找准解题方向，而且所得到的结果也是最直接最简单的，并呈现出数学的转化思想，以及化繁为简之神奇，从而使前面获取的经验逐步升华到更高的思维层次.

二、运用经验

案例5 (人教A版2-2 P50 B组第2题)

一动圆与圆x2+y2+6x+5=0外切，同时与圆x2+y2-6x-91=0内切，求动圆圆心的轨迹方程，并说明它是什么曲线.

学生首先会作出图形，然后通过图形探究三个圆内在的本质关系.设所求动圆的半径为R，根据题意得

|PO1|=2+R，|PO2|=10-R,

∴|PO1|+|PO2|=2+R+10-R=12>|O1O2|=6.

部分学生会根据这个几何关系式联想到椭圆的定义，从而先得到动圆圆心的轨迹是椭圆，然后求出椭圆的方程.学生会通过这个问题再次体会“定义优先”的经验，并且会将这一经验强化，再遇到类似问题，“定义优先”的经验会指导学生去解题.

设椭圆的短半轴长为m，双曲线的实半轴长为n， 半焦距长为c.

令|PF1|=r1，|PF2|=r2，根据椭圆和双曲线的定义得

r1+r2=2m，r1-r2=2n，则r1=m+n，r2=m-n

在△PF1F2中，由余弦定理得

即(m+n)2+(m-n)2-4c2=(m+n)(m-n),

此题抓住点P是椭圆和双曲线的公共点，充分利用了椭圆和双曲线的定义，结合余弦定理来建立等量关系，从而使问题得到解决.

三、结束语

随着学习的逐步深入，学生们在解题中就会发现，“定义优先”的经验不仅仅在解决动点的轨迹方程问题时更加便捷，而且这种经验会随着学习的深入不断得到升华.因为他们会发现，任何圆锥曲线的问题都不会脱离定义而存在，圆锥曲线的核心本质就是定义.实际上也是如此，许多复杂的解析几何问题，就是妙用圆锥曲线的定义，就可以化繁为简，达到解决问题的目的.“定义优先”的基本活动经验一定会成为学生解决圆锥曲线问题的利器.

[1]张奠宙，竺仕芬，林永伟.“数学基本活动经验”的界定与分类[J]．数学通报．2008(5).

[2]牛川勇．圆锥曲线定义在数学解题中的运用[J].语数外学习：高中数学教学，2014(9).

G632

A

1008-0333(2017)22-0033-02

龙耒(1976.8-)，湖北宜昌人，中学一级教师，硕士研究生，从事中学数学教学.杨莉(1976.1-)，湖北宜昌人，中学一级教师，本科，从事中学数学教学．

责任编辑：杨惠民]