正定矩阵及其应用

李立群

（山东农业工程学院，山东 济南250100）

正定矩阵及其应用

李立群

（山东农业工程学院，山东 济南250100）

正定矩阵是矩阵理论中非常重要的内容，可以有效地解决代数问题和分析问题.本文结合二次型和正定矩阵的关系，给出了正定矩阵的性质，通过例题阐述了判定矩阵为正定矩阵的常用方法，总结了正定矩阵在分析问题中的若干应用。

对称矩阵；正定矩阵；二次型

Abstract:Positive definite matrix plays a very important role in matrix theory and can be used to solve a lot of algebraic and analytic problems.Based on the relationship between positive definite matrix and quadratic form,this paper gives the necessary and sufficiency conditions of positive definite matrix.Two methods of the decision of positive definite matrix are given and illustrated by examples.Applications of positive definite matrix in analytic problems are also summarized.

Key words:Positive definite matrix；Symmetric matrix；Quadratic forms

1 引言

代数学是数学中的一个基础分支，不论在实际应用还是在数学理论的发展中，都有重要的地位.正定矩阵一直是矩阵分析领域非常热门的课题，它的研究最早出现在 Hermite（埃米尔特）型与二次型中，正定矩阵在物理学、几何学、概率论等学科中得到了广泛的应用.为了满足应用矩阵的学科如数学规划、投入产出的矩阵理论、计算机图像处理、现代控制等学科的需要，大量学者已开始致力于研究广义的正定矩阵 （不一定是实对称或不一定是Hermite型）[5].作为基础理论的实对称正定矩阵仍有着不可替代的作用，特别是它的判定和性质是进一步推广、应用正定矩阵理论的工具.本文从正定矩阵的定义和性质出发，总结了正定矩阵的判定条件和在分析问题中的应用.

2 正定矩阵的概念与性质

定义1[1]设

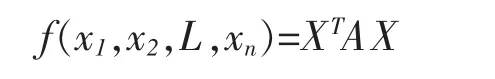
是n元实二次型（A为实对称矩阵），如果对任意不全为零的实数 c1，c2，L，cn都有

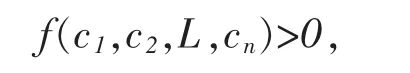
则称f为正定二次型，A为正定矩阵.

下面给出正定矩阵的一些性质.

性质1若A、B都是n阶实对称矩阵，且B是正定矩阵，则存在一n阶实可逆矩阵P使PTAP与PTBP同时为对角形.

性质2若A是实对称正定矩阵，则存在a>0，b>0使

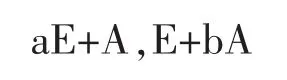
均是正定矩阵.

性质 3 若 A 是 n 阶正定矩阵，则｜A＋2E｜＞2n.

3 正定矩阵的判别方法

3.1 利用定义进行判定

对于由已知的正定矩阵证明给定的矩阵正定的问题，应用定义法最方便快捷.

例 1 设 A=（aij）n×n，B＝（aij）n×n均是正定矩阵，则 C＝aijbij称为 A 与 B 的 hadamard 乘积[5]，证明 C＝（aijbij）n×n也是正定矩阵.

证明显然矩阵C是实对称矩阵.任取X＝（x1，…xn）T≠0，由于矩阵A,B正定，所以同时有：

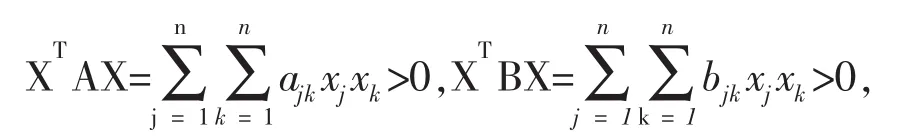
那么我们现在只需证明

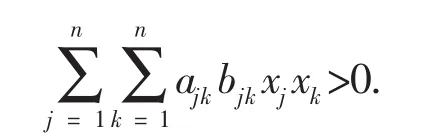
由于B是正定矩阵，故存在一个可逆矩阵Q＝（qij），使得 B＝QTQ,即

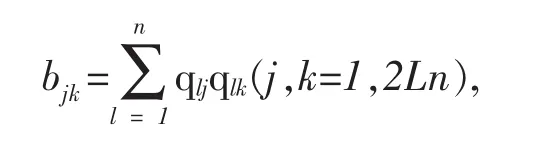
所以

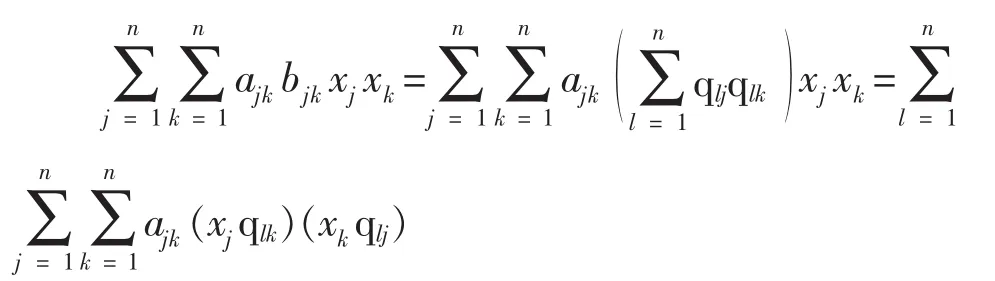
对任何

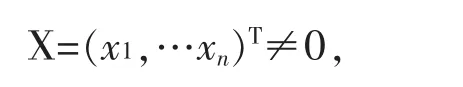
因为Q可逆，所以总存在一个l,使得

（因为不妨设x1≠0，由Q可逆知Q的第一列中必有一个元素不为零，设为q11,则x1q11≠0），又因A是正定矩阵，所以总有

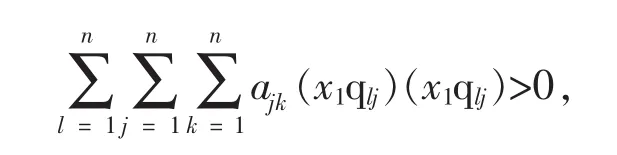
所以

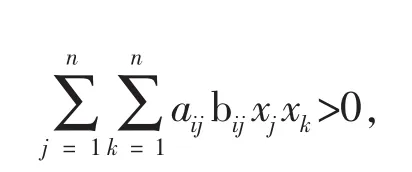
即 C＝（aijbij）n×n也是正定矩阵.

3.2 运用顺序主子式或主子式进行判定

利用顺序主子式判定正定矩阵的方法：n阶实对称矩阵A正定的充分必要条件是A的所有顺序主子式

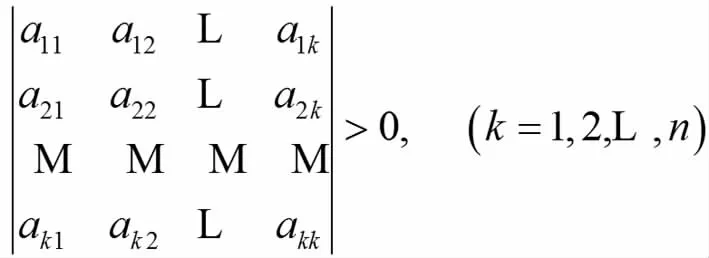
利用主子式判定正定矩阵的方法是[8]：若A是正定矩阵，那么A的主子式全大于零。其中，主子式就是行指标与列指标相同的子式.

解f的矩阵为

任取A的一个k级顺序主子式Ak，

即A的一切顺序主子式都大于零，故f为正定二次型.

4 正定矩阵在分析中的应用

4.1 正定矩阵在凸函数判定中的应用[9]

解 f（x）的 Hesse 矩阵

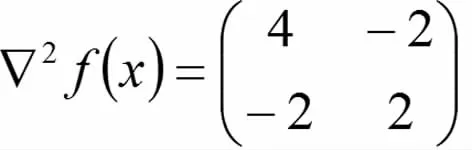
由于一阶和二阶顺序主子式都大于零，故f（x）的Hesse矩阵正定的，从而f（x）是严格凸函数.

4.2 正定矩阵在求解函数极值点中的应用[10]

定义 2 二元函数 f在点 p0（x0，y0）取得极值点的充要条件，假定f二阶连续可微偏导数，并记

它称为f在p0的Hesse矩阵，很显然Hesse矩阵为对称矩阵.

定理2（极值的充分条件）设二元函数f在点p0（x0，y0）的某邻域 U（p0）内具有二阶连续偏导函数，且 p0是 f的稳定点，则当 H（p0）是正定矩阵时，f在p0点取得极小值；H（p0）当是负定矩阵时，f在 p0点取得极大值；当是不定矩阵时，在点不取极值.

例 4 求函数 f＝3axy－x3－y3（a＞0）的极值点.

解方程组

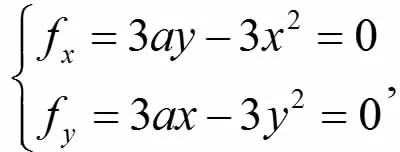
得到f的稳定点

由于

所以

因为

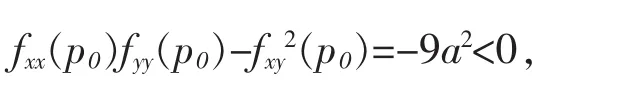
所以H（p0）是不定矩阵，由定理2知f在p0不取极值；由于

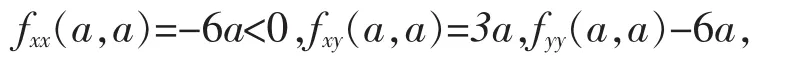
所以

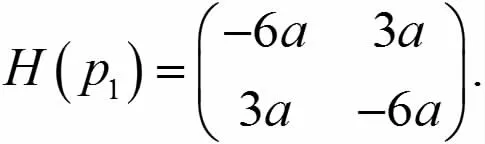
因为

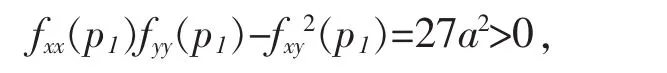
所以 H（p1）是负定矩阵，故 f在 p1取极大值，即（0，0）的极值点，（a，a）是 f的极大值点.

4.3 正定矩阵与柯西不等式[11]

定义3形如

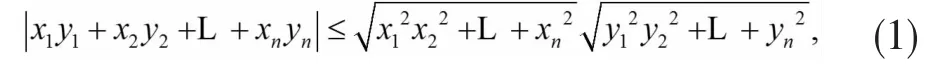
的不等式就是柯西不等式.我们将其用內积的形式来表示

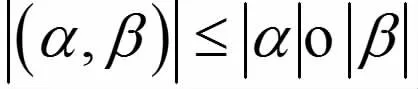
下面我们用正定矩阵来表示柯西不等式.A＝（aij）设是一个 n 阶正定矩阵， 则对任意向量 a＝（x1，x2，L，xn）与β＝（y1，y2，L，yn），定义

则可以证明由(2)定义的一定是n维向量间的內积，反之，对于n维向量间的任意一种內积，一定存在一个n阶正定矩阵

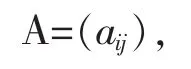
使得对任何向量

（α，β）可由(2)式来定义，因此给定一个n阶正定矩阵，在n维向量间就可以由该矩阵定义一个內积，从而得到相应的柯西不等式：

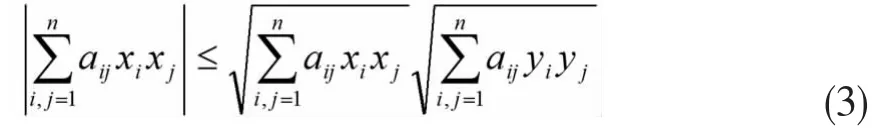
当A＝E时，(3)就变成了(1).

5 小结

正定矩阵在矩阵理论乃至整个代数学中都有着非常重要的地位，对矩阵正定性的研究，在理论和应用上都有意义.本文从正定矩阵的定义和性质出发，给出了正定矩阵的两种判定方法，总结了正定矩阵在分析中的若干应用.

[1]北京大学数学系几何与代数教研室.高等代数[M].北京：高等教育出版社,2003.

[2]徐仲、陆全等.高等代数考研教案[M].西安：西北工业大学出版社，2009.

[3]李桂荣.高等代数的方法研究[M].香港：香港亚太经济出版社，2001.

[4]Horn，R.A.and Johnson，C.R，Matrix Analysis.[M].Cambridge University Press.1985.

[5]周双.广义正定矩阵的进一步研究[J].北京交通大学硕士毕业论文，2011.

[6]姜国.正定矩阵的判定与性质[J].湖北师范学院学报,2006，26（1）:97-100.

[7]张奎、杨侠.正定矩阵的若干等价条件[J].阜阳师范学院学报,2005,22(1):19-20.

[8]朱尧辰.高等代数例选通过范例学技巧[M].哈尔滨：哈尔滨工业大学出版社,2014.

[9]张文瑜、徐成贤、朱德通，最优化方法[M].北京：高等教育出版社,2005.

[10]朱尧辰.高等代数范例选解[M].安徽:中国科技大学出版社,2015.

[11]华东师范大学数学系.数学分析(第3版)[M].北京：高等教育出版社，2004.

编辑：董刚

Positive Definite Matrix and Its Application

LI Liqun
（Shandong Agriculture And Engineering University，Jinan Shandong 250100）

O151.21

A

2095-7327（2017）-07-0028-07

李立群（1964-），男，山东菏泽人，山东农业工程学院教授，研究方向：高等数学教学。