一类二次特征值反问题及其最佳逼近

周 硕，白 媛

(东北电力大学 理学院，吉林 吉林 132012)

一类二次特征值反问题及其最佳逼近

周 硕，白 媛

(东北电力大学 理学院，吉林 吉林 132012)

讨论实双反对称矩阵和实双对称矩阵的二次特征值反问题及其最佳逼近问题，利用矩阵的奇异值分解，建立了二次特征值反问题解的充要条件，并给出了其解集的一般表达式。进而考虑了其最佳逼近问题的存在性与唯一性，得到了最佳逼近解的表达式。

二次特征值反问题；双对称矩阵；双反对称矩阵；最佳逼近；奇异值分解

二次特征值反问题是近年来工程技术领域中研究和讨论的重要课题之一。目前，二次特征值反问题的理论已被应用到结构设计[1]、阻尼系统的有限元模型修正[2-3]、阻尼振动系统的反问题[4-7]等领域中。

定义1 若A=(aij)∈Rn×n满足aij=-aji，aij=-an-j+1，n-i+1，i， j=1，2，…，n，则称A为双反对称矩阵，所有双反对称矩阵的全体构成的集合记为ABSRn×n。

定义2 若A=(aij)∈Rn×n满足aij=aji，aij=an-j+1，n-i+1，i，j=1，2，…，n，则称A为双对称矩阵，所有双对称矩阵的全体构成的集合记为BSRn×n。

本文主要讨论如下问题：

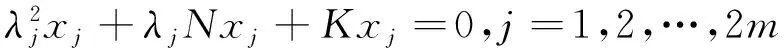
(1)

令

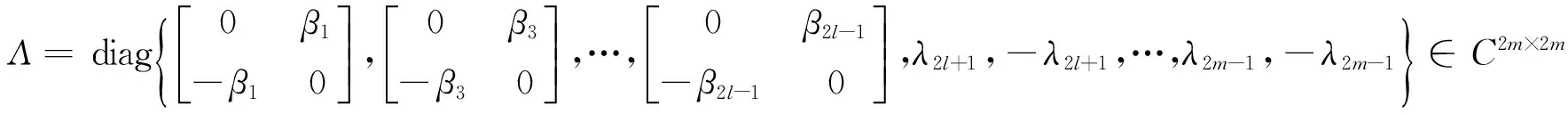
(2)

X=[x1R，x1I，…，xlR，xlI，x2l+1，…，x2m]∈Cn×2m，

(3)

则问题1等价于

XΛ2+NXΛ+KX=0.

(4)

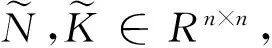
(5)

1 问题1的求解

引理1[8]已知Λ∈R2m×2m如公式(2)，则存在实反对称矩阵H，使得HΛ=ΛTHT，并且H可表示为

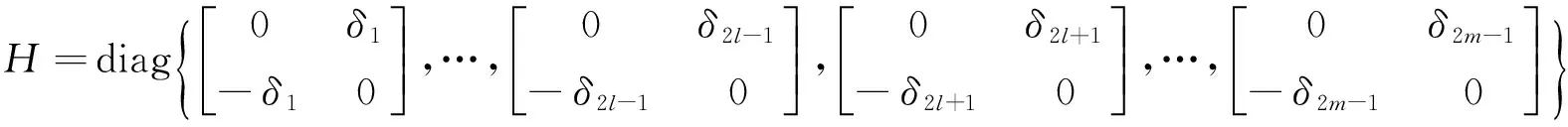
(6)

引理2[9]已知G∈SRn×n，Λ∈Rn×n，存在反对称矩阵NR∈ASRn×n，使GΛ2+NRΛ对称当且仅当存在反对称矩阵H，满足HΛ=-ΛTH，使NR=ΛTG-GΛ+H。其中，H如公式(6)所示。

对矩阵X进行奇异值分解

(7)

其中：

Q=(Q1，Q2)∈R2m×2m，Q1=(q1，q2，…，qr)∈R2m×r，Q2=(qr+1，qr+2，…，q2m)∈R2m×(2m-r).

令qj=(q1j，q2j，…，q2mj)T∈R2m，gj=GΛqj，j=r+1，r+2，…，2m；

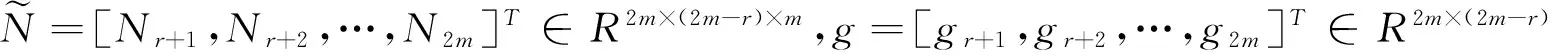
(8)

(9)

(10)

证明 将矩阵X的奇异值分解公式(7)代入公式(4)，得

(11)

记

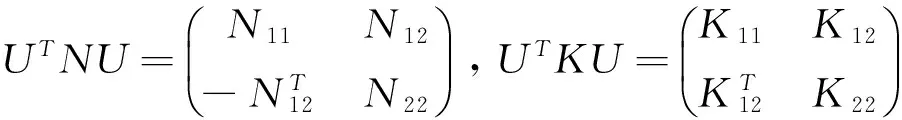
(12)

由矩阵对称性及引理2，可将问题转化为

(13)

(14)

公式(13)和公式(14)分别存在反对称解和对称解当且仅当存在反对称矩阵H，使

Hqj=GΛqj，j=r+1，r+2，…，2m，

上式等价于

(15)

(16)

(17)

经计算可得

(18)

其中：

U(1)∈OR(n-k)×(n-k)，U(2)∈ORk×k，ri=rank(Xi)，Σ1=diag(μ1，μ2，…，μri)>0，

令

应用上述引理和定理1及矩阵的奇异值分解，可得问题1有解的条件及解的形式。

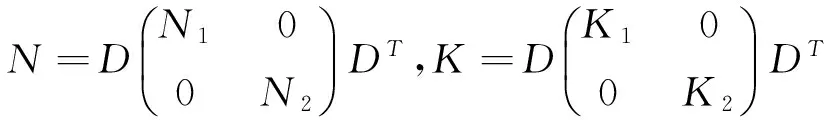
(19)

其中：

(20)

(21)

(22)

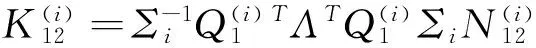
(23)

(24)

Σ1=diag{μ1，μ2，…，μr1}>0，Σ2=diag{υ1，υ2，…，υr2}>0，

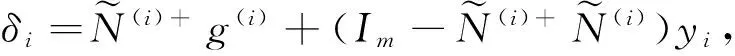
2 最佳逼近解

引理3[10]设D1，D2，F1，F2∈Rm×n，Λ=diag{λ1，λ2，…，λm}∈Rm×m，则使得

成立的最佳逼近解为

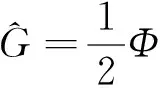
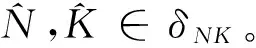
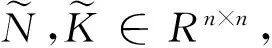
记

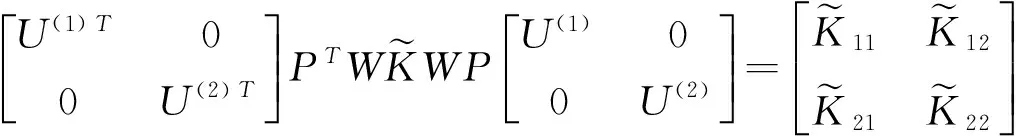
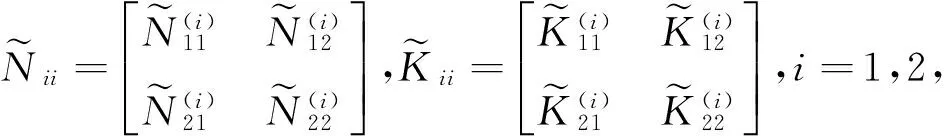
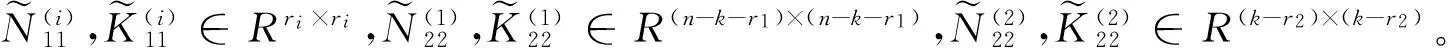
[1] K.T.Joseph.Inverse Eigenvalue Problem in Structural Design[J].Aiaa Journal，2012，30(12)：2890-2896.

[2] S.L.J.Hu，H.Li.Simultaneous mass，Damping，and Stiffness Updating for Dynamic Systems[J].Aiaa Jounal，2012，45(10)：2529-2537.

[3] X.B.Mao，H.Dai.A Quadratic Inverse Eigenvalue Problem in Damped Structural Model Updatig[J].Applied Mathematical Modeling，2016，40(13/14)：6412-6423.

[4] P.Lancaster，U.Prells.Inverse Problems for Damped Vibrating Systems[J].Journal of Sound and Vibration，2005，283(3/4/5)：891-914.

[5] J.Qian，M.S.Cheng.Quadratic Inverse Eigenvalue Problem for Damped Gyroscopic Systems[M].Amsterdam：Elsevier Science Publishers B.V.，2014.

[6] 吕晓寰，程宏伟，方彬彬，周硕.基于商奇异值分解的一类二次特征值反问题[J].东北电力大学学报，2015，35(1)：88-92.

[7] 江振，程宏伟，周硕.一类中心对称矩阵反问题的总体最小二乘解[J].东北电力大学学报，2011，31(1)：93-98.

[8] Y.X.Yuan，H.Dai.Solutions to an inverse monic quadratic eigenvalue problem[J].Linear Algebra and Its Applications，2011，434(11)：2367-2381.

[9] 周硕，韩明花，孟欢欢.用试验数据修正振动系统的双对称阻尼矩阵与刚度矩阵[J].应用数学和力学，2014，35(6)：697-711.

[10] P.Lancaster，M.Tismenetsky.The theory of matrices[M].Second Edition.New York：Academic Press.1985.

Abstract：The paper concerns the quadratic inverse eigenvalue problem of real double symmetric matrix and real double antisymmetric matrix and it’s optimal approximation problem.A necessary and sufficient condition for the solution of the quadratic inverse eigenvalue problem is constructed by singular value decomposition of matrix.the general expression of the solution to the problem is provided.Then the existence and uniqueness of the optimal approximation problem is discussed and the expression is provided for the optimal approximation problem.

Keywords：Inverse quadratic eigenvalue problem；Real symmetric matrix；Real anti-symmetric matrix；Optimal approximation；Singular value decomposition

AClassofInverseMonicQuadraticEigenvalueProblem

ZhouShuo，BaiYuan

(Science College，Northeast Electric Power University，Jilin Jilin 132012)

O241.6

A

2016-12-06

国家自然科学基金项目(11072085)；吉林省自然科学基金项目(201115180)

周 硕(1968-)，男，博士，教授，主要研究方向:科学与工程计算.

电子邮箱：：zhou-shuo@163.com(周硕)；1366039009@qq.com(白媛)

1005-2992(2017)05-0096-06