基于模糊粒计算的风电功率实时预测研究

杨 茂，杨春霖

(东北电力大学 电气工程学院，吉林 吉林 132012)

基于模糊粒计算的风电功率实时预测研究

杨 茂，杨春霖

(东北电力大学 电气工程学院，吉林 吉林 132012)

随着风电接入电网规模的日益扩大，其波动对电网的影响也日趋增大，而准确的风电功率预测可以有效地降低其对电力系统稳定性的影响，因此风电功率预测对接入大规模风电的电力系统稳定运行具有相当重要的意义。提出一种模糊粒计算和支持向量机相结合的风电功率实时预测方法，利用模糊粒计算将风电功率时间序列划分为简单的子序列时间窗口，同时把具有相似属性的对象组合在一起，通过提取核心信息减少冗余，利用支持向量机法对子序列进行预测，得到最终的预测值。以东北地区某两个风电场的实测数据为例，根据国家能源局文件中的指标验证了模型有效性。

风电功率；实时预测；模糊集；粒计算

风电功率的随机性、波动性和不确定性一直以来是影响风电大规模接入电网的主要原因，而准确的风电功率预测能够最大限度的减少其对电力系统的影响，因此风电功率的预测已成为了电力系统安全稳定运行必不可少的关键一环[1，2]，而公认的提高预测精度的最主要途径是改进预测方法，国内和国外的有关学者在风电功率预测方面做了很多工作，一种风电功率组合预测方法在文献[3]中被提出，组合的原则是采用交叉熵理论把预测模型的组合过程类比为信息融合的过程，模型优点是考虑了预测信息的相互融合和支撑，但弱化了历史功率样本间的内在联系，会造成某些重要信息的缺失以致于对预测结果产生影响。一种基于支持向量机(Support Vector Machine，SVM)和经验模态分解的短期风电功率组合预测方法在文献[4]中被提出，其对风速时间序列进行平稳化处理，得到具有相同特征尺度的风速数据序列，但此过程会丢失一些体现数据基本特征的信息，对预测精度的影响在所难免。文献[5]提出了一种基于主成分与人工神经网络的预测模型，提取出原始序列的主成分，将其作为神经网络的输入对输出功率进行预测，但此过程也不能避免传统神经网络中诸如学习速度慢、存在局部极小点等各种固有缺陷。文献[6]提出了一种基于自适应扰动量子粒子群算法参数优化的支持向量机预测模型，在参数寻优的过程中加入了一种自适应早熟判定准则，有效的克服了支持向量机参数选择中依靠历史经验的弊端，但没有对历史数据间的联系进行研究。文献[7]提出了一种基于动态权重的风电功率组合预测方法，将不同模型组合起来，用合作对策法和动态权重法确定各单一模型的权重，然后用组合模型进行预测，但使用的预测算法都为基本算法，没有使用预测效果相对较好的智能预测算法。

本文提出了一种基于模糊粒计算和支持向量机的预测模型，模糊粒计算是把具有相似属性的对象集合在一起，依据在各个粒度水平上的需要得到不同的信息粒，进而可以将问题的求解转化到不同的粒度水平上；因而原始数据的基本特点被完全保存，系统的透明度也随之提高。另一方面模糊粒计算在信息粒化过程中抓住数据的核心，减少冗余信息，从而获得系统行为的简单表示，这可以大大降低问题求解的复杂度，为实现高精度的风电功率实时预测奠定了基础。

1 模糊信息粒基本理论及评价指标

模糊信息粒化是信息处理的典型方法，对于风电功率预测而言，将相应时间段的数据作为一个信息粒来研究，通过模糊信息粒化的方法进行有效数据的提取，能够有效简化运算，改善预测结果[8-10]。

1.1 粒计算

粒是指元素的类、群或聚类。信息粒化是把一类对象划分为若干个粒的过程，每一个粒是基于相似性、不可区分性关系和泛函性聚集得到的一个对象的组合。对微粒大小的平均度量被称为粒度。在阐明信息时，从不同的层面对数据信息和知识抽象度用粒度来度量、分析和处理[11-13]。

定义1：粒度

设R：U→P(U)⟹U=∪Gi，i∈τ，则Gi为一个信息粒子，{Gi}i∈τ是论域的一种粒度。其中P(U)表示论域U的幂集，R表示不可区分关系、功能相近关系、等价关系等的函数。∀i∈τ，i≠j，当Gi∩Gj=∅时，{Gi}i∈τ为论域的无重叠粒度划分，即：{Gi}i∈τ=[U]，否则称{Gi}i∈τ是论域的一种覆盖，简记为：{Gi}i∈τ=。

定义2：粒子大小

目前，进行粒计算时，主要有三种应用模型，即商空间模型、模糊集合模型、粗糙集模型，本文主要采用基于模糊集的粒计算模型[15]。

1.2 模糊集

令U为论域，给定U的一个次序分割集为Ui={ui1，ui2，…，uin}，其元素uij为常数。Λi={Λi1，Λi2，…，Λin}，定义在Λi为论域Ui上的模糊集合，其中：

(1)

其中：fΛi为定义在Λi上的模糊隶属函数；fΛi(uij)为uij在模糊集Λi上的隶属度的值，1≤i≤n。

对模糊集合Λi的隶属度通常用公式(2)来计算。

(2)

其中：lin为子区间的长度；t为时刻；Λij为集合Λi中的第j个元素。

将一定时间分辨率下的信息假设为一个粒子进行分析时，可以利用粒计算提取出各个粒子中所蕴含的有效信息，形成模糊粒，模糊粒既能将复杂时间序列划分为简明的时间窗口又能确保其基本联系不被破坏，同时也将具有相似属性的对象组合在一起，通过提取核心信息减少冗余，提高了系统透明度[16-18]，也能够简化计算过程，并提高预测精度。

1.3 模型评价指标

国家能源局在关于风电并网的文件中规定的有关风电功率预测的主要指标有日平均预测计划曲线准确率、日平均预测计划曲线合格率和全天预测结果均方根误差[19]。

(1)全天预测结果均方根误差(EDRMSE)，其定义如下式：

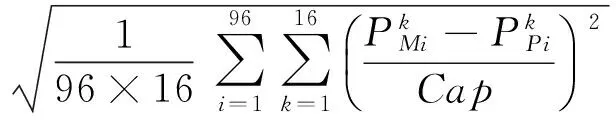
(3)

(2)日平均预测计划曲线准确率(r1)，定义如下式：

(4)

(3)日平均预测计划曲线合格率(r2)，定义如下式：

(5)

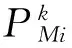
2 模糊粒计算预测模型

本文将一定时间分辨率下的有效信息作为一个粒子进行分析，通过粒化技术来提取各个粒子的有效信息。将一个时段下的风电功率序列X视为一个窗口进行模糊化，即在风电功率序列X上构建一个模糊粒子P，即一个能够合理描述X的模糊概念G(以X为论域的模糊集合)，一旦确定了G，即可得到模糊粒子P，其实质就是对G的隶属函数A=f(u)的确定过程。

具体实现步骤如下：

模糊信息粒化的主要过程可分为两步：窗口划分、信息模糊化。窗口划分即根据需要对整个的预测序列进行分割，形成若干个小的子序列，每一个子序列可视为一个操作窗口；信息模糊粒化的实质为一个有效信息提取的过程，也就是使用特定规则对获得的每一个窗口的信息进行模糊化处理，得到一系列模糊集。根据预测的需要对窗口进行划分处理，建立一个合理的模糊集，使其能够取代原来窗口中的有用信息是模糊化过程的核心。对原始数据模糊粒化效果如图1所示。

为了使得预测数据处于同一数量级，避免较大值对小值的覆盖，使其具有可比性，利用下式：

(6)

其中：xl为归一化的下界；xu为归一化的上界；xmin，xmax分别为原始数据的最大值与最小值；x为待归一化的原始数据。

将模糊粒化后的数据由公式(6)进行归一化后如图2所示。

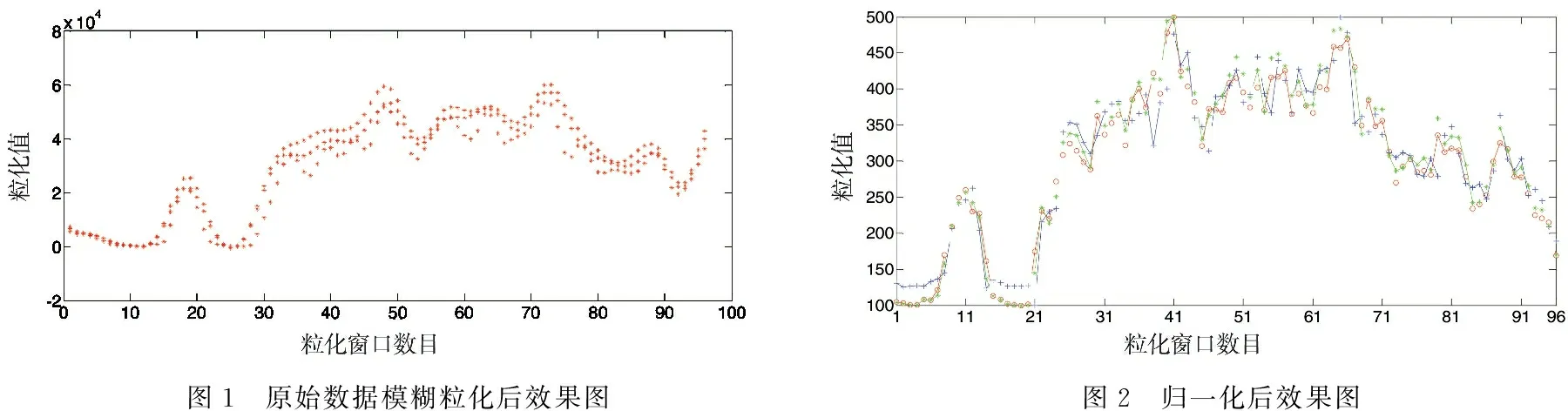
图1 原始数据模糊粒化后效果图图2 归一化后效果图

算法实现过程图如下：

图3 算法实现过程图

3 算例分析

选取我国东北地区A、B两个风电场2015年7月份和8月份两个月采样间隔为1 min的历史功率数据作为研究样本，两风电场都有177台风机，单机容量均为1.5 MW，总装机容量为265.5 MW。利用本文提出的模型对A、B两风电场未来一天(2015年7月16日)风电功率进行实时预测(训练集为2015年7月1日-7月15日数据)，每天进行96次的风电功率实时滚动预测，每次预测的风电功率为16个时间点[20-22]。

首先，对训练数据进行模糊信息粒化，以15 min(15个采样点)为一个窗口，即可将训练集划分为1440个窗口，在每个窗口中对训练数据利用公式(2)进行模糊粒化，该过程中在每个窗口形成了3个模糊信息粒，再分别将这些模糊信息粒进行归一化，之后再利用支持向量机模型进行预测，将预测后的值进行反归一化处理，能够获得不同的模糊信息粒的预测功率值，再由等权重法将不同模糊粒预测的功率值组合便可得到最终的预测值。

图4、图5为不同预测模型对不同风电场预测结果，指标如表1、表2所示。

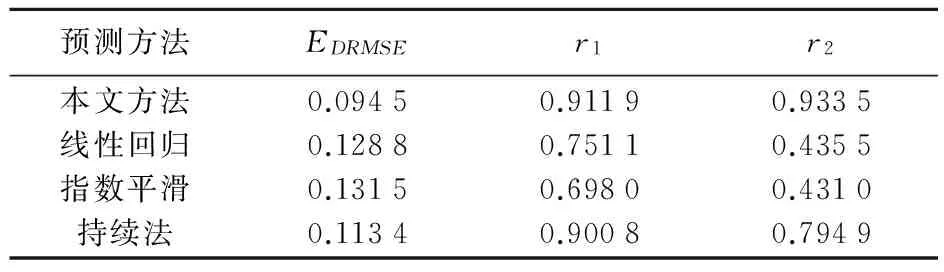
表1 风电场A未来一天不同预测方法的评价指标

表2 风电场B未来一天不同预测方法的评价指标

图4 风电场A未来四小时不同方法预测值图5 风电场B未来四小时不同方法预测值

由表1可知，四种预测方法中本文方法的全天预测均方根误差最小为0.094 5，其次为持续法的0.113 4和线性回归法的0.128 8，误差最大的为指数平滑法的0.131 5；日平均预测计划曲线准确率只有基于粒计算模型和持续法达到了0.9以上分别为0.911 9和0.900 8，指数平滑和线性回归法分别为0.698 0和0.751 1；本文方法的日平均预测计划曲线合格率为0.933 5，同样优于其他三种模型；而线性回归、指数平滑和持续法分别为0.435 5、0.431 0和0.794 9。显然本文提出的模糊粒计算模型的三个评价指标均优于其他三个经典的预测模型，在表二中虽然本文方法的预测结果全天预测结果均方根误差大于持续法，但合格率和准确率分别为0.996 7和0.924 1均高于持续法的0.877 6和0.913 5，同时线性回归和指数平滑的各项指标均差于本文所提出的方法，由此可以确定该方法较持续法、线性回归和指数平滑法预测性效果更加良好。四种不同预测方法分别对A、B两风电场功率进行预测的准确率如图6和图7所示。

图6 风电场A未来一天各预测点准确率图7 风电场B未来一天各预测点准确率

为了进一步验证模型的有效性，对A、B两风电场未来一个月(2015年8月)进行实时预测(原始训练集为2015年7月17日-2015年7月31日，每预测一步训练集将增加一个点形成新的训练集，训练集窗口的划分和模糊粒的形成同上文)，结果如表3、表4所示。

表3 风电场A未来一个月不同模型评价指标的平均值

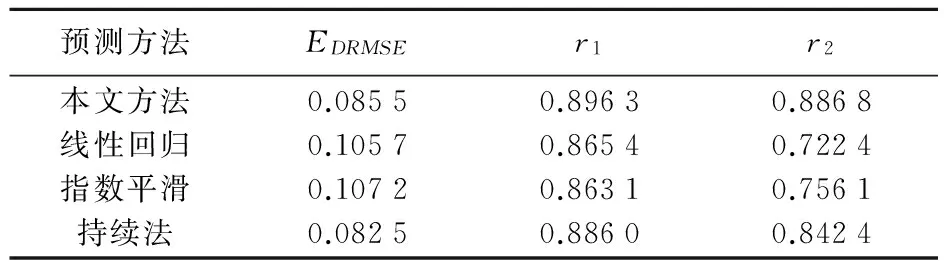
表4 风电场B未来一个月模型评价指标的平均值

在表3中对风电场A利用不同的模型进行未来一个月的预测，本文模型预测结果的平均均方根误差为0.103 9，显然为最小，其次为持续法的0.124 7，线性回归和指数平滑法预测效果最差,均方根误差分别为0.141 6和0.144 6，本文模型的合格率和准确率同样较其他三种算法更高分别为0.884 5、0.896 1，而其余三种算法的合格率则较低，分别为线性回归的0.728 5和0.718 0,指数平滑的0.677 0和0.737 6,持续法的0.873 7和0.793 1。表4为对风电场B利用不同模型预测的结果，本文方法预测结果的评价指标同样明显优于其他三个模型。

综上，可知本文所提的基于模糊粒计算的风电功率预测模型较持续法、指数平滑法和线性回归法具有更高的预测精度。

4 结 论

本文提出了一种基于模糊粒计算的预测模型，将相应时间尺度下的有效信息作为一个粒子来进行研究，通过粒化技术来提取各个粒子的有效信息。信息粒化技术具有对大规模数据进行挖掘并根据需要有效提取有用信息的能力，支持向量机有具有较好的学习能力。两种方法相结合建立的预测模型可有效进行风电功率预测。

以东北地区某两个风电场A、B的历史功率数据作为研究样本将基于模糊粒计算模型的预测结果与持续法、线性回归法、指数平滑法比较可知，本文提出的粒计算模型的三个评价指标均为最优。由此可知基于粒计算的模型预测效果明显优于其它三种预测模型，预测精度显著提高。

[1] 刘波，贺志佳，金昊.风力发电现状与发展趋势[J].东北电力大学学报，2016，36(2)：7-13.

[2] 杨茂，陈新鑫，张强，等.基于支持向量机的短期风速预测研究综述[J].东北电力大学学报，2017，37(4)：1-7.

[3] 陈宁，沙倩，汤奕，等.基于交叉熵理论的风电功率组合预测方法[J].中国电机工程学报，2012，32(4)：29-34，22.

[4] 叶林，刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J].中国电机工程学报，2011，31(31)：102-108.

[5] 周松林，茆美琴，苏建徽.基于主成分分析与人工神经网络的风电功率预测[J].电网技术，2011，35(9)：128-132.

[6] 卢志刚，陈月敏.基于改进聚类的输电线路参数多代理辨识与估计[J].电气工程学报，2015，10(4)：70-81.

[7] 杨茂，季本明.基于局域一阶加权法的风电功率超短期预测研究[J].东北电力大学学报，2015，35(5)：6-10.

[8] 吴珺.基于粒计算的数据挖掘研究及应用[D].武汉：武汉理工大学，2009.

[9] 伍军云，张丽萍，洪胜华.粒计算及其在数据挖掘中的应用[J].科技广场，2005，34(06)：43-45.

[10] 顾洁，杨熠娟，施伟国.基于粒计算的电力系统中长期负荷动态聚类预测模型[J].电网技术，2009，33(20)：120-124.

[11] 邱桃荣.面向本体学习的粒计算方法研究[D].北京：北京交通大学，2009.

[12] 王贺，胡志坚，仉梦林.基于模糊信息粒化和最小二乘支持向量机的风电功率波动范围组合预测模型[J].电工技术学报，2014，29(12)：218-224.

[13] 孙文越，张建华，王如彬.基于粒计算的模糊神经建模方法在电能输出预测中的应用[J].华东理工大学学报：自然科学版，2015，41(4)：529-537.

[14] 朱旻辰.基于加权SVM与粒计算的金融时间序列波动范围预测研究[D].上海：上海交通大学，2014.

[15] 孙轶轩.基于数据挖掘的道路交通事故分析研究[D].北京：北京交通大学，2014.

[16] 王军.粒计算及其在图像分类中的应用研究[D].南昌：南昌大学，2007.

[17] 左吉峰.信息粒度与决策树[D].保定：河北大学，2009.

[18] 邓飞，潘华.基于粒计算的入侵检测系统研究[J].现代电子技术，2011，34(10)：115-117.

[19] 国家能源局.风电厂功率预测预报管理暂行办法[S].北京：国家能源局，2011.

[20] 王永翔，陈国初，张鑫.基于PF-RBF神经网络的短期风电功率预测[J].上海电机学院学报，2014，17(6)：324-328，333.

[21] 杨茂，孙涌，王东，等.基于时间序列的多采样尺度风电功率多步预测研究[J].电测与仪表，2014，51(23)：55-59，109.

[22] 严干贵，王东，杨茂，等.两种风电功率多步预测方式的分析及评价[J].东北电力大学学报，2013，33(1/2)：126-130.

Abstract：With the expansion of the wind power the fluctuation of the impact on the grid is increasing，and the accurate wind power forecasting can valid decrease its affect to power system stability，so the wind power prediction is very important to the stability of power system operation，when large-scale wind power access to power system.This paper proposed a kind of fuzzy granular computing and support vector machine united wind power forecasting method based on fuzzy granular computing，the wind power time series is divided into sub-sequences of simple time window，while the objects with similar attributes together，reduce redundancy by extracting core information，prediction using support vector machine sub sequence，to get the final prediction value.Taking the measured data of a two wind farm in Northeast China as an example，the validity of the model is verified on the basis the index of the National Energy Bureau.

Keywords：Wind power；Real-time forecasting；Fuzzy set；Granular computing

ResearchonWindPowerReal-TimeForecastingBasedonFuzzyGranularComputing

YangMao，YangChunlin

(Electrical Engineering College，Northeast Electric Power University，Jilin Jilin 132012)

TM614

A

2017-03-12

国家重点基础研究发展计划项目(973计划) (2013CB228201)；国家自然科学基金(51307017)；吉林省产业技术研究与开发专项项目(2014Y124)；吉林省科技发展计划(20140520129JH).

杨 茂(1982-)，男，博士，副教授，主要研究方向：电力系统分析与风力发电技术.

电子邮箱：yangmao820@163.com(杨茂)；425161220@qq.com(杨春霖)

1005-2992(2017)05-0001-07