基于Archard模型的车轮磨耗对车辆动力学性能的影响

姚永明 李国芳 丁旺才

兰州交通大学机电工程学院，兰州，730070

基于Archard模型的车轮磨耗对车辆动力学性能的影响

姚永明 李国芳 丁旺才

兰州交通大学机电工程学院，兰州，730070

为了研究车轮磨耗对高速列车动力学性能的影响，建立了车辆动力学和车轮磨耗耦合模型。考虑车辆通过一条由直线和曲线组成的典型线路工况，采用Non-elliptic模型计算轮轨接触斑上的车轮磨耗量，以累积车轮型面磨耗量及更新型面外形。采用Archard磨耗模型研究车轮面磨耗的分布与发展，以车轮踏面磨耗深度达到0.1 mm为型面更新的条件进入下一个磨耗循环的计算。最后加载磨耗后的车轮型面，研究磨耗对车辆系统通过曲线线路时的动力学性能的影响。

车轮磨耗；动力学性能；Non-elliptic模型；Archard模型

Abstract:To study the effects of wheel wear on high-speed train dynamics performance, a multi-body system dynamics and vehicle wear wheel coupling model was established. The vehicles were considered through a typical line conditions consisting of straight lines and curves. Non-elliptic model was used to calculate the amounts of wear on the wheels, the amounts of wear of the wheel profile cumulations and then the profile shapes were updated. Using Archard wear model, wheel tread wear depth of 0.1 mm was considered for profile update conditions, and then the next calculation cycle wear began. Finally, wear wheel profiles were loaded to study the effects of wear on the dynamics performance of the vehicle systems through the curves.

Keywords:wheel wear; dynamics performance; Non-elliptic model; Archard model

0 引言

近年来，随着我国旅客列车的多次提速和重载铁路的发展，轮轨之间相互作用愈来愈剧烈，车轮和钢轨之间的磨耗问题日益严重，加大了车辆的维修工作量和运营成本，车轮型面磨耗也严重影响了车辆的运行平稳性和安全性[1-2]。罗仁等[3-4]基于FASTSIM计算了轮轨接触斑上的车轮磨耗量，研究了高速列车轮轨参数对车轮踏面磨耗的影响。ROVIRA等[5]基于超声波反射法和FASTSIM解决了轮轨接触时表面粗糙的问题，并用T·伽马法估算了轮轨磨耗量。李霞等[6-9]提出基于车辆轨道垂横向耦合动力学、轮轨滚动接触力学和材料摩擦磨耗模型的车轮磨损计算模型,并研究了相应的数值方法。IGNESTI等[10]为车轮和钢轨轮廓磨耗演化的预测开发了新的磨损模型，并通过多体动力学软件SIMPACK进行了验证。ZHAI等[11]为减少车辆通过曲线线路时的钢轨侧磨，研究了重载铁路曲线钢轨研磨轮廓设计的优化方案。GAN等[12]通过计算轮轨接触带宽和其变化率的方法评估了S1002CN型车轮踏面质量。

本文建立了车辆动力学和轮对磨耗耦合模型，采用Archard磨耗预测方法，研究了车轮型面磨耗的分布与发展;加载磨耗后的车轮型面，继而研究了磨耗对车辆系统动力学性能的影响。

1 模型的建立

1.1 动力学模型

建立高速客车横向、垂向耦合动力学模型，模型包括1个车体、2个构架、4个轮对和8个轴箱，其中车体、构架和轮对各有6个自由度(分别考虑其浮沉、横摆、伸缩、摇头、点头、侧滚)，每个轴箱有一个自由度(仅考虑轴箱的点头振动)，整个车辆系统共有50个自由度，如表1所示。车辆一系悬挂由钢弹簧、垂向液压减振器和转臂轴箱组成，其中钢弹簧和轴箱转臂定位刚度采用线性弹簧模型，一系垂向液压减振器考虑了其非线性特性；二系采用空气弹簧支撑车体，并安装有抗蛇行减振器、横向液压减振器、垂向液压减振器和横向止挡，其中空气弹簧采用线性弹簧建模，抗蛇行减振器、横向减振器、垂向液压减振器和横向止挡均考虑其非线性特性。该车辆系统动力学模型如图1所示。

表1 车辆系统主要参数Tab.1 The main parameters of vehicle system

图1 车辆系统动力学模型Fig.1 Vehicle dynamics model

1.2 磨耗仿真计算流程

根据车轮踏面形状和车辆系统动力学性能之间的约束关系，建立车辆磨耗仿真流程，如图2所示。从图2中可以看出，本文车轮磨耗研究主要由车辆动力学仿真、局部轮轨接触计算、车轮磨耗计算和车轮型面更新这四部分组成。

图2 车轮磨耗计算图Fig.2 Flow diagram of wheel wear

列车在实际线路运行时，车轮型面的磨耗量是逐渐连续增大的。数值仿真中可能做不到型面的实时更新，只能在型面磨耗到一定程度后再更新，即踏面外形的变化是离散的，根据文献[13-14]，磨耗0.1 mm更新一次型面是合适的，因此本文采用0.1 mm作为型面更新的判据。钢轨采用60 kg/m的钢轨，车轮半径为460 mm，轨底坡度为1/40，轨距为1435 mm，轨道激励采用UIC_good不平顺，采用Non-elliptic模型计算轮轨蠕滑力。仿真中车辆结构对称，假设线路上左曲线和右曲线对称布置，并且列车不掉头往返运行，则1、4位轮对4个车轮的磨耗相同，2、3位轮对4个车轮的磨耗也相同。根据高速线路的特点，选择表2所示的典型直线和曲线线路工况。

表2 线路参数设置Tab.2 Parameter setting of line

1.3 Archard磨损模型

用于车辆磨耗计算的材料摩擦磨损模型主要有两种，一种是基于轮轨接触斑能量耗散与磨耗指数的磨损模型，另一种是基于轮轨法向力和接触斑滑动量的Archard磨损模型。本文采用Archard磨损模型计算车轮的磨耗深度。在Archard模型中，材料的磨耗体积与法向力和滑动距离的乘积成正比，与材料的硬度成反比，即

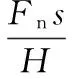
(1)

式中，Vwear为磨耗体积；k为磨耗系数，其大小由接触点的滑动速度和接触压力决定；H为材料的硬度；Fn为轮轨法向力；s为滑动距离。

JENDEL[15]应用Archard磨损模型，将接触区域分成计算单元，得到每个计算单元中心的磨耗深度：

(2)

式中，pz为计算单元上的正压力密度。

根据Archard磨损模型，磨耗系数k由计算单元上正压力和滑动速度决定，如图3所示。图3中的磨耗系数是在干燥清洁的条件下试验得到的，为了方便计算，不同区域里的磨耗系数本文取其中间值代替，即k1=350×10-4，k2=k4=5×10-4，k3=35×10-4。

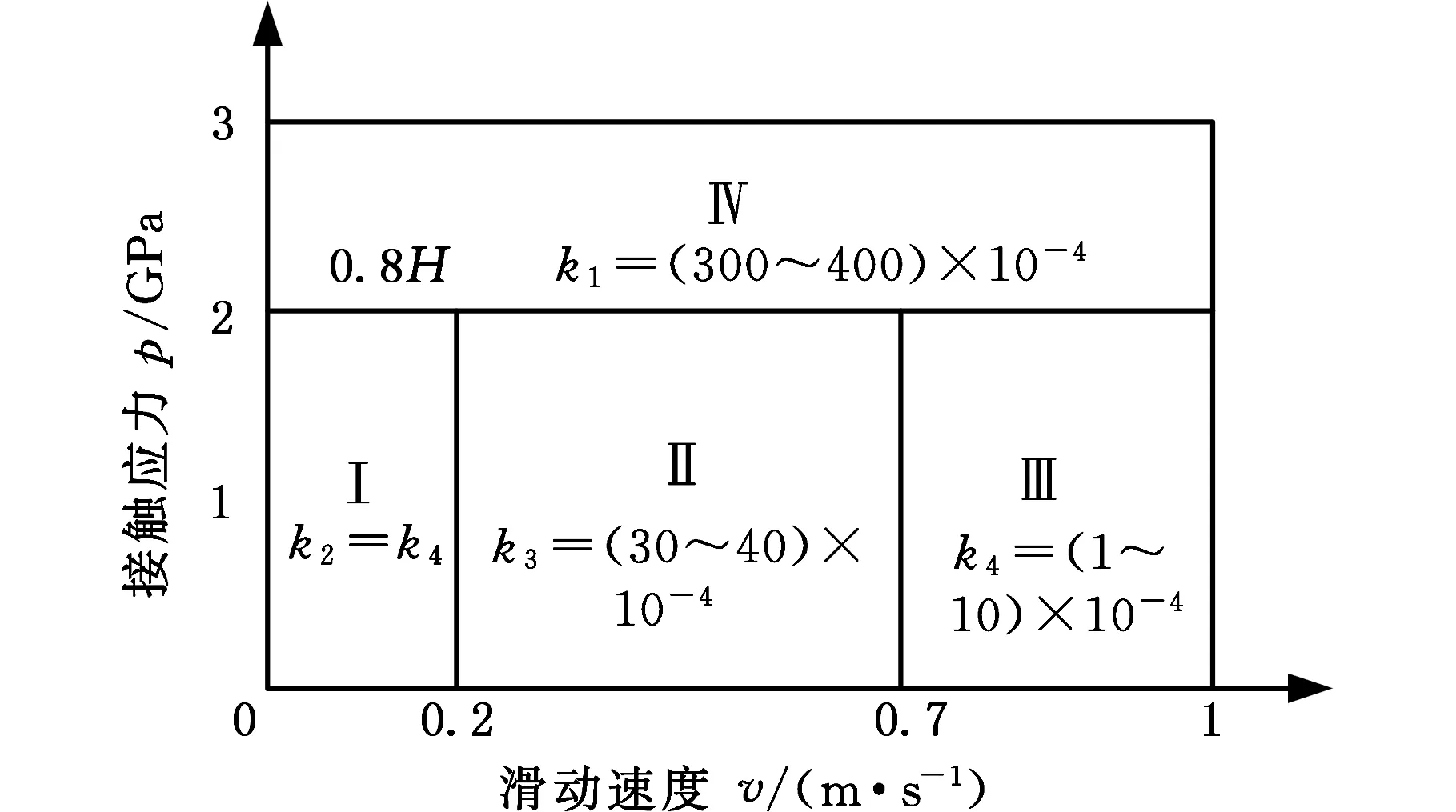
图3 Archard磨耗系数分布情况Fig.3 Wear coefficient distributionof Archard

2 计算结果与分析

2.1 磨耗速率

图4示出了车轮踏面磨耗速率随运行里程的变化情况。由图4可以看出，1位轮对磨耗速率随着运行里程的增加先增大后减小，当车辆运行到34.3×104km时磨耗速率达到最大值1.316 mm2/(104km)；2位轮对磨耗速率随着运行里程的增加先增大后减小最后再增大，当车辆运行到79.79×104km时磨耗速率达到最大值1.268 mm2/(104km)。由于前轮导向作用，1位轮对的磨耗速率明显比2位轮对的磨耗速率快。

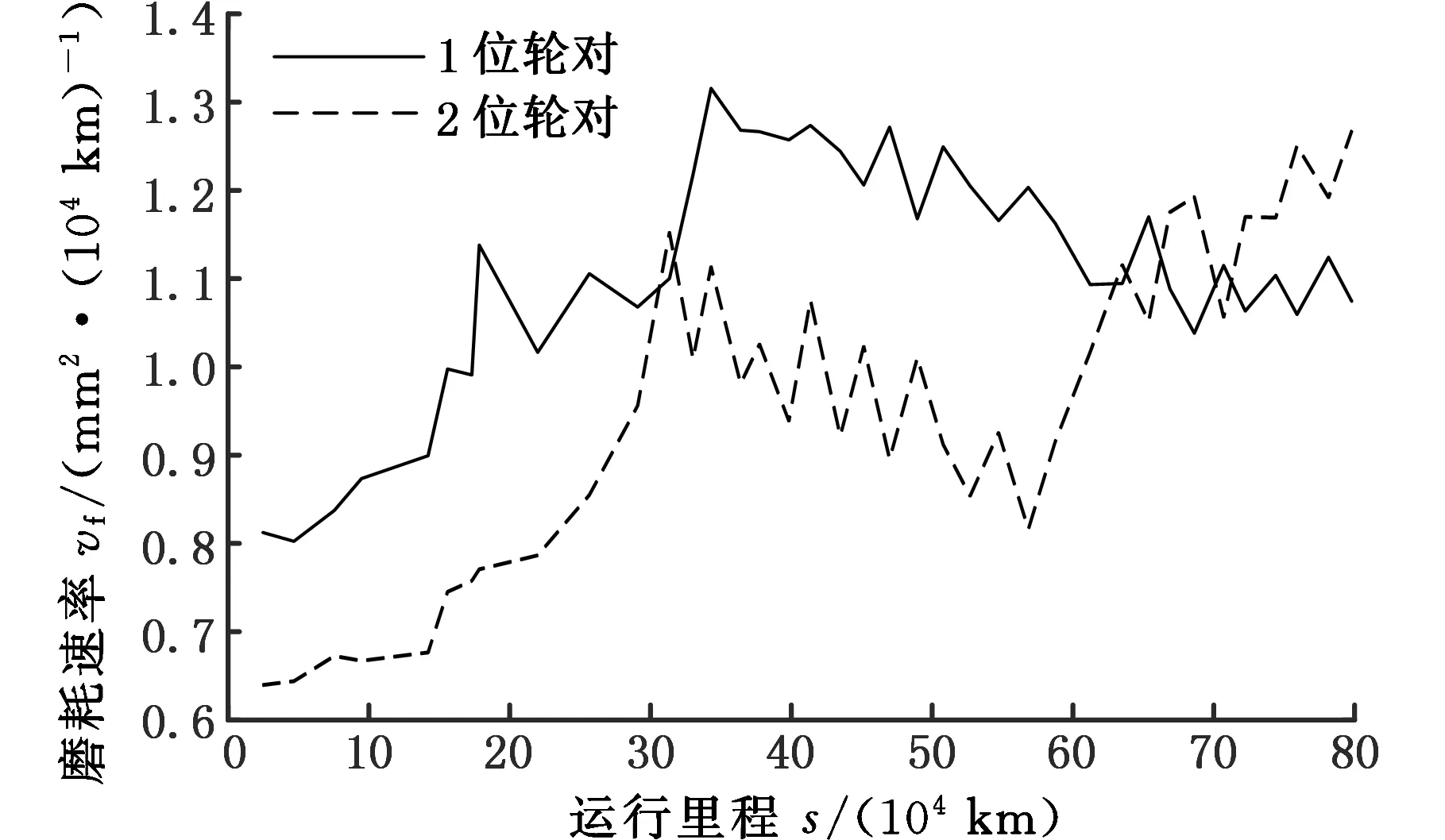
图4 车轮磨耗速率Fig.4 Wear rate of wheel

2.2 磨耗深度

图5为车轮名义滚动圆处车轮踏面磨耗深度随运行里程的变化曲线，从图中可以看出1位轮对车轮名义滚动圆处车轮踏面的磨耗深度大于2位轮对车轮名义滚动圆处车轮踏面的磨耗深度；车轮名义滚动圆处车轮踏面处磨耗深度随运行里程基本呈线性变化，1位轮对磨耗深度在运行里程为(30～50)×104km时呈非线性变化，2位轮对磨耗深度在运行里程为(60～80)×104km时呈非线性变化，其原因可能是该车辆系统在该运行里程区域内车轮处于非稳定磨耗期。

图5 车轮名义滚动圆处踏面磨耗深度随运行里程的变化Fig.5 The variation of tread wear depth with running distance at the nominal rolling circle

表3示出了该车在仿真和试验两种情况下车轮名义滚动圆处车轮踏面磨耗深度随运行里程的变化，从表3中可以看出无论是仿真还是试验，1位轮对车轮名义滚动圆处车轮踏面的磨耗深度大于2位轮对车轮名义滚动圆处车轮踏面的磨耗深度；车轮名义滚动圆处车轮踏面处磨耗深度随运行里程基本呈线性变化，并且从表3中还可以看出试验时车轮磨耗量明显大于仿真时车轮磨耗量，这是因为列车在运行过程中线路条件比仿真时线路条件恶劣。

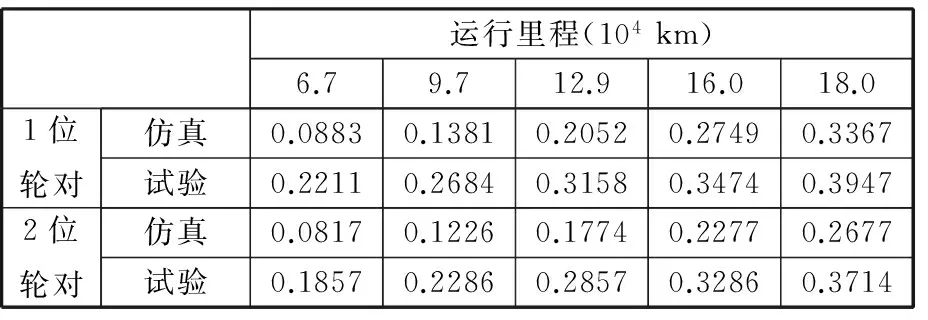
表3 仿真和试验时车轮名义滚动圆处车轮踏面磨耗深度Tab.3 Simulated and measured wheel depth of wheel tread wear at rolling wheel mm

2.3 磨耗型面

(a)1位轮对

(b)2位轮对图6 仿真磨耗后车轮踏面外形和磨耗深度分布Fig.6 Shape and depth distribution after simulated wear

图6所示为在不同运行里程下车轮踏面外形磨耗发展和磨耗深度分布情况。对比1、2位轮对可以看出，随着运行里程的增加，1、2位轮对踏面外形发展变化规律基本一致，磨耗主要发生在踏面横向坐标为-35～38 mm范围内，由于计算中采用的线路曲线半径较大，车辆悬挂定位参数设置合理，所以轮缘磨耗不严重，磨耗主要发生在轮缘根部和踏面中部，主要表现为踏面圆周磨耗，圆周磨耗量随着运行里程的增加而线性增大。

从车轮踏面磨耗深度发展情况来看，轮缘根部磨耗和踏面中部磨耗比较严重。对比1、2位轮对可以看出，1位轮对比2位轮对的磨耗严重，这是由于前轮的导向作用，增加了车轮的磨耗。

图7示出了该动车试验时运行18×104km的车轮踏面外形和磨耗深度分布情况。从图7中可以看出,随着运行里程的增加，1、2位轮对踏面外形发展变化规律基本一致，磨耗主要发生在踏面中部，主要表现为踏面圆周磨耗，圆周磨耗量随着运行里程的增大而线性增大，1位轮对比2位轮对的磨耗严重。

(a)1位轮对

(b)2位轮对图7 试验磨耗后车轮踏面外形和磨耗深度分布Fig.7 Shape and depth distribution after test wear

2.4 等效锥度

等效锥度是用于表征轮轨接触几何关系的重要参数之一，高速列车车轮踏面磨耗与等效锥度密切相关，较小的等效锥度有利于磨耗，较大的等效锥度可能造成列车失稳，因此，等效锥度是轨道、车辆及多体动力学仿真计算、车辆运行性能评定和试验验收等的主要指标。

在铁路的应用中，轮对横向位移为3 mm的等效锥度值通常用来表征轮轨接触几何特性，如果没有其他说明，等效锥度通常被理解为轮对3 mm横向位移的锥度。等效锥度计算中认为轮对运动是周期的或随机的。欧洲铁路系统中关于机车车辆子系统、基础设施子系统的TSI标准中，对等效锥度的极限值规定如表4所示。

表4 TSI中等效锥度的设计极限值Tab.4 The profile equivalent limit value of TSI

图8所示为踏面等效锥度与运行里程之间的关系曲面，随着车辆运行里程的增大，轮对踏面上的等效锥度不断增大。车辆运行37×104km到53×104km之间时，1位轮对踏面最大等效锥度达到0.25，车辆运行到39.83×104km时，轮对横向位移3 mm处的等效锥度达到最大值0.189；车辆运行到27.5×104km到34×104km之间时，2位轮对踏面最大等效锥度达到0.25，车辆运行到79.79×104km时横向位移3 mm处的等效锥度达到最大值0.343。对比1、2位轮对的等效锥度可以看出，2位轮对比1位轮对踏面等效锥度先达到设计极限值。

(a)1位轮对

(b)2位轮对图8 踏面等效锥度与运行里程之间的关系曲面Fig.8 The relation curved surface between the equivalent conicity and the running distance

2.5 等效接触角

图9所示为踏面等效接触角与运行里程之间的关系曲面，随着车辆运行里程的增大，轮对踏面上的等效锥度不断增大,2位轮对等效接触角比1位轮对接触角增幅大。车辆运行里程在20×104km以内时，轮对的等效接触角稍微增大，且1位轮对的等效接触角增幅大于2位轮对等效接触角增幅；车辆运行里程超过20×104km以后，轮对的等效接触角迅速增大，并且2位轮对等效接触角增速明显快于1位轮对等效接触角增速。

(a)1位轮对

(b)2位轮对图9 踏面等效接触角与运行里程之间的关系曲面Fig.9 The relation curved surface between the equivalent contact angle parameter and the running distance

3 型面磨耗对车辆系统曲线通过的影响

为研究车轮磨耗后对车辆系统曲线通过的影响，分析了车辆在半径为4000 m的曲线上运行时的安全性指标和平稳性指标。车辆通过曲线时轮对采用LMA型磨耗型踏面，钢轨采用CHN60钢轨，轨底坡度为1/40，UIC_good轨道谱作为轨道激励输入。曲线路段采用直线L1-缓和曲线P1-圆曲线S-缓和曲线P2-直线L2的标准高速铁路线型，曲线线路示意图见图10。

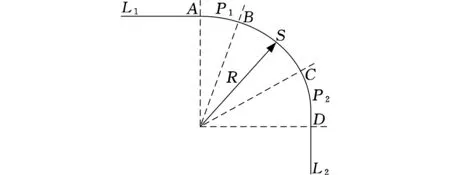
图10 曲线线路示意图Fig.10 Schematic diagram of curve line

3.1 型面磨耗对车辆运行安全性的影响

图11所示为不同磨耗型面对车辆运行安全性的影响情况。由图11a可以看出，随着车辆运行里程的不断增大，车轮踏面磨耗深度增大，1位、2位轮对的横向位移量不断减小。新轮(s=0)时1位轮对最大横向位移为14.77 mm，最小值出现在车辆运行79.793×104km时，减小到10.42 mm；新轮时2位轮对最大横向位移为13.68 mm，最小值出现在车辆运行79.793×104km时，减小到9.044 mm。车辆系统受到横向激励后很快就回复到中心。

由图11b可以看出，1位轮对的轮轴横向力随着运行里程的增大先增大后缓慢减小，新轮时轮轴横向力为13.52 kN，最大值出现在车辆运行39.8258×104km时，达到16.76 kN，增幅为23.96%；2位轮对的轮轴横向力随车辆运行里程的增大先缓慢增大，然后迅速减小，最后又迅速增大，新轮时轮轴横向力为10.71 kN，最大值出现在车辆运行79.793×104km时，达到13.02 kN，增幅为21.57%。

由图11c可以看出，1位轮对的脱轨系数随着运行里程的增大先增大后缓慢减小，新轮时脱轨系数为0.1687，最大值出现在车辆运行29.0835×104km时，达到0.2206，增幅为22.53%；2位轮对的轮轴横向力随车辆运行里程的增大先缓慢增大，然后迅速减小，最后又迅速增大，新轮时轮轴横向力为0.1307，最大值出现在车辆运行79.793×104km时，达到0.1545，增幅为18.21%。

由图11d可以看出,车轮磨耗对轮重减载率影响不大，新轮时1位轮对的轮重减载率为0.3679，最大值出现在车辆运行里程为29.0835×104km时，达到0.3951，增幅为7.39%；新轮时2位轮对的轮重减载率为0.3316，最大值出现在车辆运行里程为9.4679×104km时，达到0.3343，增幅为0.81%。

(a)轮对横向位移

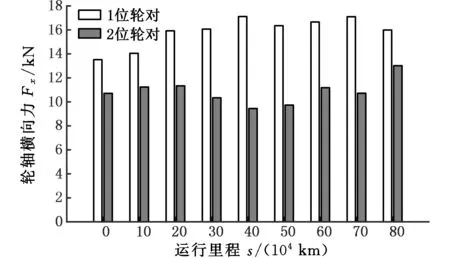
(b)轮轴横向力

3.2 型面磨耗对车辆运行平稳性的影响

图12所示为不同磨耗型面对车辆运行平稳性的影响。由图12a可以看出，随着车辆运行里程的不断增加，车轮踏面磨耗深度增大，车辆系统的横向Sperling指数增大，垂向Sperling指数基本保持不变。新轮时车辆系统的横向Sperling指数最小，为2.15，车辆运行79.79×104km时横向Sperling指数最大为2.27，增幅为5.58%。由于踏面产生了凹型磨耗，引起轮轨之间的振动冲击，导致车辆系统的横向Sperling指数增大，车辆系统横向的平稳性降低。

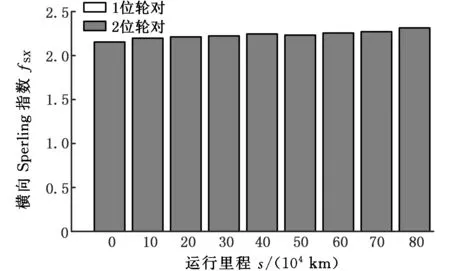
(a)横向Sperling指标

(b)垂向Sperling指标图12 平稳性指标Fig.12 Sperling index

4 结论

(1)车轮的磨耗速率随着车辆运行里程的增加先增大后减小，仿真过程中，当车辆运行到34.3×104km时，1位轮对磨耗速率达到最大值，车辆运行到79.79×104km时，2位轮对磨耗速率达到最大值。

(2)随着运行里程的增加，仿真跟试验的轮对踏面外形发展变化规律基本一致，由于仿真跟试验的工况不可能完全一致，导致仿真的过程中车轮踏面的磨耗量要小于试验时车轮踏面的磨耗量。

(3)车轮磨耗严重影响了车辆的安全性，随着车辆运行里程的增大，车辆系统的安全性下降。

(4)车轮磨耗对车辆的横向平稳性影响比较明显，随着车辆运行里程的增加，车轮磨耗深度加大，车辆系统的横向平稳性指标线性减小；车轮磨耗对车辆的垂向平稳性影响不明显。

(5)车轮磨耗严重影响了车辆运行的安全性和平稳性，为了保证车辆的运行安全和乘客的乘坐舒适性，在车辆运行达到一定里程后需要对车轮进行镟修。

[1] 沈钢,王浩川,韩明盛.具有独立轮轻轨列车的脱轨问题及轮缘侧面磨耗研究[J].铁道学报,2006,28(4):49-53. SHEN Gang,WANG Haochuan,HAN Mingsheng. Study on Derailment and Flange Side-wear of Tramway Vehicles with Independently-rotating Wheels[J].Journal of the China Railway Society,2006,28(4):49-53.

[2] 刘宏友,王为,李亨利,等.青藏客车轮缘异常磨耗分析[J].铁道车辆,2008,46(5):1-6. LIU Hongyou,WANG Wei,LI Hengli,et al.Analysis of Abnormal Wear of Wheel Flanges for Qingzang Passenger Cars[J]. Rolling Stock,2008,46(5):1-6.

[3] 罗仁,曾京,戴焕云,等.高速列车车轮磨耗预测仿真[J].摩擦学学报,2009,29(6):551-558. LUO Ren,ZENG Jing,DAI Huanyun,et al. High-speed Train Wheel Wear Prediction Simulation[J]. Tribology,2009,29(6):551-558.

[4] 罗仁,曾京,邬平波,等.高速列车车轮参数对车轮踏面磨耗的影响[J].交通运输工程学报,2009,9(6):47-53. LUO Ren, ZENG Jing, WU Pingbo, et al. Influence of Wheel/Rail Parameters on Wheel Profile Wear of Hing-speed Train[J]. Journal of Traffic and Transportation Engineering,2009,9(6):47-53.

[5] ROVIRA A,RODA A,MARSHALL M B,et al. Experimental and Numerical Modelling of Wheel-rail Contact and Wear[J]. Wear,2011,271:911-924.

[6] 李霞,金学松,胡东.车轮磨耗计算模型及其数值方法[J].机械工程学报,2009,45(9):193-200. LI Xia, JIN Xuesong, HU Dong. Theoretical Model and Numerical Method of Wheel Profile Wear[J]. Journal of Engineering Mechanics,2009,45(9):193-200.

[7] 李霞,温泽峰,金学松.地铁车轮踏面异常磨耗原因分析[J].机械工程学报,2010,46(16):60-66. LI Xia, WEN Zefeng, JIN Xuesong. Analysis of Abnormal Wear Causations of Wheel Tread on Metro Vehicles[J]. Journal of Engineering Mechanics,2010,46(16):60-66.

[8] 李霞,金学松,温泽峰,等.计算铁路车轮轮周磨耗量的两种方法对比[J].工程力学,2011,28(1):205-211. LI Xia, JIN Xuesong, WEN Zefeng, et al. Comparison of Two Methods for the Calculation of Railway Wheel Circumference Wear[J]. Engineering Mechanics,2011,28(1):205-211.

[9] 李霞,温泽峰,金学松.重载铁路车轮磨耗和滚动接触疲劳研究[J].铁道学报,2011,33(3):28-33. LI Xia, WEN Zefeng, JIN Xuesong. Investigation intoWheel Wear and Fatigue of Heavy-haul Railways[J]. Journal of the China Railway Society,2011,33(3):28-33.

[10] IGNESTI M,INNOCENTI A,MARINI L,et al. Development of a Model for the Simultaneous Analysis of Wheel and Rail Wear in Railway Systems[J]. Multibody System Dynamics,2014,31(2):191-240.

[11] ZHAI Wanming, GAO Jianmin, LIU Pengfei, et al.Reducing Rail Side Wear on Heavy-haul Railway Curves Based on Wheel-rail Dynamic Interaction[J]. Vehicle System Dynamics, 2014,52(S):440-454.

[12] GAN Feng,DAI Huanyun, GAO Hao,et al. Wheel-rail Wear Progression of High Speed Train with Type S1002CN Wheel Treads[J]. Wear,2015,328/329:569-581.

[13] ENBLOM R,BERG M. Simulation of Railway Wheel Profile Development due to Wear-Influence of Disc Braking and Contact Environment[J]. Wear,2005,258:1055-1063.

[14] JENDEL T, BERG M. Prediction of Wheel Profile Wear Methodology and Verification[J]. Vehicle System Dynamics,2002,37(S):502-513.

[15] JENDEL T.Prediction of Wheel Profile Wear Comparisons with Filed Measurement[J]. Wear,2002,253:89-99.

(编辑王艳丽)

InfluencesofWheelWearonDynamicsPerformanceofVehiclesBasedonArchardModel

YAO Yongming LI Guofang DING Wangcai

School of Mechatronic Engineering,Lanzhou Jiaotong University,Lanzhou，730070

U271.91

10.3969/j.issn.1004-132X.2017.19.007

2016-11-10

国家自然科学基金资助项目(11462011,51665027)；甘肃省教育厅高等学校科研项目(2013B-024)；甘肃省科技计划项目(1606RJZA037,17JR5RA098)

姚永明，男，1990年生 。兰州交通大学机电工程学院硕士研究生。主要研究方向为车辆系统动力学。发表论文3篇。李国芳,男，1979年生。兰州交通大学机电工程学院讲师。丁旺才( 通信作者)，男，1964年生。兰州交通大学机电工程学院教授。E-mail:dingdd@163.com。