互联悬架液压参数灵敏度分析及优化

周 兵 陈逸彬 耿 元 任程远

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

互联悬架液压参数灵敏度分析及优化

周 兵 陈逸彬 耿 元 任程远

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

针对液压参数对互联悬架输出响应影响程度大小的问题，建立了四自由度液压互联悬架半车侧倾耦合频域模型，通过计算系统的传递函数及施加路面激励，得到了悬架模型在垂直模态和侧倾模态下的加速度谱密度响应。采用基于模糊灰色关联的灵敏度分析方法对悬架垂直模态和侧倾模态进行分析，得到了各液压参数的灰色关联度。运用多目标优化算法NSGA-Ⅱ，以两种模态下的悬架响应为优化目标，对灵敏度大的液压参数进行了优化。优化后两种模态下加速度功率谱密度峰值及加速度均方根值均有减小，液压互联悬架平顺性得到提高。

液压互联悬架；加速度输出谱密度；灵敏度分析；模糊灰色关联；多目标优化

Abstract:In view of the effects of hydraulic parameters of interconnected suspensions on the suspension responses, a four DOF hydraulically interconnected suspension half car roll frequency domain model was established. According to the system transfer function and road inputs the bounce acceleration power spectrum density and roll acceleration power spectrum density were calculated. By using the sensitivity analysis method based on fuzzy grey correlation, the influence degree of hydraulic parameter on bounce response and roll response was carried out. NSGA-Ⅱ method was used by taking as optimization object under two modes suspension responses. The obtained results indicate that the peak value of acceleration power spectral density is decreased as well as the acceleration root mean square value of the acceleration, and the ride comfort of the hydraulic interconnected suspension is improved.

Keywords:hydraulically interconnected suspension; acceleration power spectrum; sensitivity analysis; fuzzy grey correlation;multi-objective optimization

0 引言

互联悬架是指通过特定结构或装置使原本独立的车轮在运动过程中对其他车轮产生特定影响的悬架系统[1-2]。单个车轮的运动会使其他车轮的运动状态及弹簧力发生相应变化，从而使整个悬架系统产生紧密的关联性。与传统悬架相比，互联悬架的优势在于它可兼顾调控车辆的平顺性及侧倾稳定性。液压互联悬架中液压油管有同向互联和反向互联两种连接方式，其中,反向互联悬架能够在不影响垂直振动的前提下增大侧倾刚度，提高车辆行驶的稳定性。

近年来，国内外学者对互联悬架开展了大量研究。GARROTT等[3]通过实车验证研究了液压互联悬架的动态特性；赵春明[4]利用功率键合图法建立了互联油气悬架模型；DING等[5-7]对两轴车互联悬架俯仰特性进行研究，提出了一种适用于三轴货车的互联悬架，分析了互联悬架对三轴车车体振动的影响。

综上，模型的建立及动态分析为互联悬架的主要研究内容，而涉及分析和优化液压参数对悬架系统动态响应影响的研究较少。本文建立四自由度液压互联悬架半车侧倾耦合频域模型，采用基于模糊灰色关联的灵敏度分析方法[8-9]，分析蓄能器和阻尼阀的液压参数对加速度输出谱密度的影响，并通过NSGA-Ⅱ算法按敏感程度大小对这些参数进行多目标优化。

1 四自由度液压互联悬架建模

1.1 悬架系统建模

四自由度半车防侧倾液压互联悬架的模型如图1所示[10]，其中，半车模型选取在侧倾振动平面，传统悬架系统中的减振器由液压互联系统代替，轮胎系统由弹簧阻尼系统代替，其簧下质量分别用mL和mR表示，簧上质量为M，侧倾转动惯量为I，图2为图1点划线框所示的液压系统具体示意图。当系统存在位移变量y=[yLyRyvθ]T时，根据牛顿第二定律建立机械系统动力学微分方程：

(1)

f1(t)=M1Ap(t)A=diag(A1,A2,A3,A4)

p(t)=[p1p2p3p4]T

式中，M、C、K分别为质量、阻尼、刚度矩阵；f1(t)为液压系统作用力；A为液压缸面积矩阵；p(t)为左右液压缸作动器上下腔的压力矩阵；M1为转换矩阵；lL、lR分别为左右轮至车身中心的距离；f2(t)为路面输入力。

图1 液压互联悬架示意图Fig.1 Schematic of hydraulically interconnected suspension

图2 互联悬架液压系统示意图Fig.2 Schematic diagram of hydraulic system of interconnected suspension

图2中，液压互联悬架流体管路采用基于分布参数的二维黏性可压缩流体直管动力学模型[11]，油管的连接方式采用反向互连。q1、q2、q3、q4分别为左右作动器上下腔室的流量，R1、R2、R3为阻尼阀。液压系统由a、b两条回路构成。整个机械液压耦合系统的刚度和阻尼由流经油管、阻尼阀、蓄能器、三向接头等液压元件的进出流量进行调整。对液压系统建模时，将液压元件沿液压回路进行分段离散化并建立各个液压元件的传递函数矩阵，沿液体流动方向将各个传递函数矩阵相乘得到液压回路通路阵,从而得到液压系统的阻抗矩阵。线路a的通路阵

Xa=P11→12P10→11V9→10P8→9J5→8P4→5V3→4P2→3P1→2

式中，P为液压悬架系统中油管管路通路阵；V为阻尼阀通路阵；J为蓄能器阻尼阀组合元件的通路阵。

(3)

同理，对于b线路,有

(4)

在频域中，流量Q(s)和压力P(s)的线性传递关系由阻抗阵Z(s)描述，即

Q(s)=Z-1(s)P(s)

(5)

结合式(3)和式(4)有

(6)

因此，阻抗矩阵

(7)

悬架运动过程中，作用于车身的合力来源于回路中液体的流动。假设忽略任何流量泄漏，液体流量q(q=[q1q2q3q4]T)与悬架位移的关系为

(8)

(9)

综上，将机械系统动力学微分方程式(1)及液体流量式(8)进行拉氏变换，并结合式(5)得系统动力学方程:

[s2M+s(C-M1AZ(s)AM2)+K]Y(s)=F2(s)

(10)

式中，F2(s)与f2对应，为路面输入力。

1.2 目标函数

路面具有不平度时，悬架左右两车轮因此产生跳动，频域路面模型采用C级路面，常见的路面对半车模型的输入谱密度矩阵为

(11)

对式(10)进行变形，可得到系统加速度对路面输入的传递函数矩阵

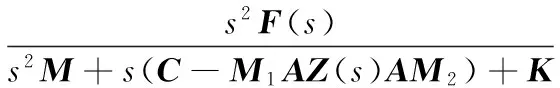
(12)

式中，F(s)为路面系数矩阵。

(13)

表1 液压互联悬架系统仿真参数Tab.1 The simulation parameters of hydraulically interconnected suspension

2 互联悬架灰色关联度分析

2.1 模糊灰色关联分析模型

悬架模型中，液压系统参数共同影响着悬架的输出响应，在对液压系统参数进行优化前，需要对这些参数进行灵敏度分析，找出对响应输出影响大的参数。

聚类分析是数理统计中的一种多元分析方法，它用数学方法定量地确定样本的亲疏关系，从而客观地划分类型。灰色关联分析是基于相似或相异程度的发展趋势来衡量各个因素相关度的，相关水平越高，事物之间相似水平就越高。目前应用较多的灰色关联分析模型是邓氏灰色关联分析模型[13]。模糊聚类分析与灰色关联分析都被广泛应用于自然及社会科学领域。其中, 模糊聚类适用于所属类具有模糊性的研究对象, 灰色关联分析适用于信息不完整的研究系统。

通过对液压互联悬架进行灰色关联分析，可得到各液压参数的灵敏度，具体实现过程如下：

(1)参考序列及比较序列设定。参考序列中的数据表示系统某种行为特性，第T组参考序列

(14)

比较序列由影响系统特性的数据所组成，可写为如下形式：

(15)

其中，m为影响系统特性数据的个数，则其中一组影响数据可用xts表示,s=1, 2, …,m，对这些因素进行n组实验，第i次实验可以表述为xts(i)，i=1, 2, …,n。

(2)原始序列量纲一化处理。由于要研究的液压互联悬架中液压参数具有不同的量纲，为了在计算之前使各个因素具有相同的影响水平，有必要对不同量纲的参数进行量纲一化处理。本文采用数据区间化方法，即

X=[x(1)x(2) …x(n)]

(16)

(17)

k=1, 2, …，n

(3)模糊隶属度余弦值计算。在计算两参数之间相似程度时，由于夹角余弦法具有不受两因素制约关系，可直接对其进行相似度计算。表现形式为

(18)

(4)灰色关联系数计算。关联系数表示对应两点之间的关联程度，反映了影响因素与对应响应之间的密切程度关系。关联系数可写为

(19)

(20)

(21)

Δis(k)=|YT(k)-Xti(k)|

(22)

式中，Δmin为YT与XT中相应因素间的绝对值差的最小值；Δmax为相应的最大绝对值差；Δts(k)为YT中k点与XT中k点的绝对差值；β为分辨系数，其在关联系数中表征了最大绝对差值对关联系数的影响程度，在对β赋值的过程中，要兼顾关联度整体性及稳定性，过大过小的取值都将对两者间的关联程度产生错误引导。

(5)欧氏灰色关联度计算。在对两序列相似水平进行计算的过程中，本文以模糊数学中欧氏距离[14]来表示序列间的相似水平，在此，定义权向量w来表示不同因素在序列中的影响程度：

wts=(w1s,w2s,…,wns)s=1, 2, …,m

(23)

则其灰色关联度的计算公式为

(24)

(6)模糊灰色关联度计算。灰色关联度及模糊隶属系数共同之处在于二者都体现了研究对象之间的相似程度和差异水平,不同之处在于前者适用于不完全信息的研究体系，后者适用于具有模糊性、不确定性的研究对象，模糊隶属系数在克服了参数量纲差异的前提下，反映了两参数的相似程度。将两方法结合形成模糊灰关联度[9,15]，它对处理难排序、难分类的问题具有一定优势。综合式(18)及式(24)，可得到模糊关联度

(25)

2.2 稳态响应影响因素灵敏度分析

通过对液压互联悬架中液压参数进行灰色关联分析，得垂直模态及侧倾模态下，液压参数对输出响应的关联度值，即灵敏度值，如图3所示。

图3 垂直和侧倾模态灰色关联度柱状图Fig.3 Fuzzy grey correlation degree of bounce and roll modes

结果表明，在垂直模态下，连接液压缸上下腔的阻尼阀参数对垂直响应的影响较大而对侧倾响应影响较小；相反，在侧倾模态下，蓄能器及连接蓄能器的阻尼阀参数对垂直响应的影响较小而对侧倾响应的影响较大；并且，整体来说，这6个液压参数对垂直响应的影响比对侧倾响应的影响要小。这是由于在车身垂直振动时，只有较少的油液流进和流出蓄能器，而通过连接上下腔的阻尼阀在左右液压缸之间进行交换的油液较多;而在车身侧倾运动中，在车体的侧向运动作用下，拉伸或挤压液压缸使得油液频繁流出与流进蓄能器，此时液压油路的压力随之减小或增大，从而在液压缸处产生合力来阻止车身的侧倾。由上所述，蓄能器和阻尼阀系数为影响互联悬架动态响应的关键参数，所以，本文选取蓄能器工作压力p1、预充压力p2、连接液压缸上下腔阻尼阀压力泄漏系数R1、R2这4个变量作为设计变量。

3 基于NSGA-Ⅱ算法的多目标优化

DEB等[16]于 2002 年对传统的 NSGA 算法进行了改进，提出了 NSGA-Ⅱ算法(non-dominated sorting genetic algorithm-Ⅱ)。上述优化模型属于多目标优化问题， NSGA-Ⅱ算法因其具有强大的全局寻优能力，在避免了目标偏好性的同时保持了各个目标的相对独立性，通过引入精英策略，提高了优化结果的精度，通过采用拥挤度和拥挤度比较算子，使种群均匀地分布在目标空间，提高了种群的多样性，因此可有效解决该多目标优化问题。

设上述多目标优化问题数学模型为

(26)

表2 设计变量的取值范围Tab.2 Range of design variable in the fluid system

本文NSGA-Ⅱ参数设置如下：种群规模为300，进化代数为100，交叉概率为0.8，变异概率为0.5。

考虑到低速工况中，对车辆的侧倾稳定性要求不高，对垂直模态响应有较高要求，故以舒适性为主要优化目标；高速工况中侧倾稳定性影响着车辆安全性，故优化目标主要考虑提高车辆的抗侧倾能力。本文在对目标函数进行优化时选择中速工况，同时考虑低速时的舒适性及高速时车辆侧倾稳定性。设车辆仿真速度为60km/h，通过NSGA-Ⅱ算法，可得到优化目标函数一组Pareto解集，经过对Pareto解集中各个目标函数权衡分析，得到该多目标优化问题的最优解，如表3所示，Pareto解集如图4所示。

表3 设计变量初始值与优化值

图4 优化目标Pareto解集Fig.4 Optimal objects Pareto solution set

为了验证优化结果的有效性，将优化后的设计变量代入悬架模型中并进行仿真，得到优化前后悬架模型响应输出对比情况，如图5、图6所示。

图5 优化前后垂直模态响应对比Fig.5 Bounce mode response contrast

图6 优化前后侧倾模态响应对比Fig.6 Roll mode response contrast

在对车辆平顺性进行评价时[17]，常采用加速度均方根值作为评价指标，计算式为

(27)

式中，f0、f1分别为上下限频率，常取0.5～80 Hz。

优化前后悬架输出响应对比如表4所示，结合上述优化结果可清楚看到，通过采用优化后的设计方案，液压互联悬架垂直模态和侧倾模态下的加速度功率谱密度峰值及加速度均方根值均得到明显的减小。优化过程中兼顾了互联悬架垂直模态和侧倾模态响应，使车辆平顺性及侧倾稳定性得到协同提高。

表4 优化前后悬架输出响应对比Tab.4 Comparison of suspension output response

4 结论

(1)根据系统的频响函数和路面输入分别得到垂直模态和侧倾模态下的加速度功率谱密度响应。采用基于模糊灰色关联的灵敏度分析方法，可得到液压系统各参数对车身垂直加速度响应和侧倾加速度响应影响程度大小，充分证明了这种灵敏度分析方法在处理难排序、难分类问题的优势。

(2)采用NSGA-Ⅱ方法对高灵敏度参数进行多目标优化，液压互联悬架的动态响应均有所降低，车辆平顺性及侧倾稳定性得到协同提高，为后续悬架优化设计提供了参考。

[1] SMITH M C, WALKER G W. Interconnected Vehicle Suspension[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2005,219(3):295-307.

[2] 丁飞. 重型商用车液压互联悬架系统特性分析及设计[D]. 长沙：湖南大学,2013. DING Fei. Characteristic Analysis and Design of Hydraulically Interconnected Suspensions for Commercial Heavy Trucks[D]. Changsha: Hunan University,2013.

[3] GARROTT W, HOWE J, FORKENBROCK G. Results from NHTSA’s Experimental Examination of Selected Maneuvers that May Induce On-road Untripped, Light Vehicle Rollover[J]. SAE Technical Paper,2001-01-0131.

[4] 赵春明. 油气悬架系统动力学理论及其相关控制技术研究[D].大连：大连理工大学，1998. ZHAO Chunming. Theory and Its Associated Control Technology Research for Pneumatic Suspension System Dynamics[D]. Dalian: Dalian University of Technology,1998.

[5] DING F, HAN X, ZHANG N, et al. Characteristic Analysis of Pitch-resistant Hydraulically Interconnected Suspensions for Two-axle Vehicles[J]. Journal of Vibration and Control,2015,21(16):3167-3188.

[6] 丁飞，张农，韩旭. 安装液压互联悬架货车的机械液压多体系统建模及模态分析[J]. 机械工程学报,2012,48(6):116-123. DING Fei, ZHANG Nong, HAN Xu. Modeling and Modal Analysis of Multi-body Truck System Fitted with Hydraulically Interconnected Suspension[J]. Journal of Mechanical Engineering,2012,48(6):116-123.

[7] DING F, HAN X, LUO Z, et al. Modelling and Characteristic Analysis of Tri-axle Trucks with Hydraulically Interconnected Suspensions[J]. Vehicle System Dynamics,2012,50(12):1877-1904.

[8] WEI G W. Gray Relational Analysis Method for Intuitionistic Fuzzy Multiple Attribute Decision Making[J]. Expert Systems with Applications,2011,38(9):11671-11677.

[9] 龙艳平.动力锂离子电池充电过程热模拟及模糊灰色关联分析[D].长沙:湖南大学,2012. LONG Yanping. Thermal Simulation on Dynamic Lithiumion Battery during Charge and Its Fuzzy Grey Relational Analysis[D]. Changsha: Hunan University,2012.

[10] ZHANG N，SMITH W A，JEYAKUMARAN J. Hydraulically Inter-connected Vehicle Suspension: Background and Modelling[J].Vehicle System Dynamics,2010,48(1):17-40.

[11] STECKI J, DAVIS D. Fluid Transmission Lines-distributed Parameter Models Part 1: a Review of the State of the Art[J]. Proc. Inst. Mech. Eng. A, Power Process Eng.,1986,200:215-228.

[12] NEWLAND D E. An Introduction to Random Vibrations, Spectral and Wavelet Analysis[M]. 3rd ed. London: Longman,1993.

[13] 田民, 刘思峰, 卜志坤. 灰色关联度算法模型的研究综述[J]. 统计与决策,2008(1):24-27. TIAN Min, LIU Sifeng, BU Zhikun. A Review on Model of Gray Relative Level[J]. Statistics and Decision,2008(1):24-27.

[14] KRISHNAMOORTHY A, BOOPATHY S R, PALANIKUMAR K, et al. Application of Grey Fuzzy Logic for the Optimization of Drilling Parameters for CFRP Composites with Multiple Performance Characteristics[J]. Measurement,2012,45(5):1286-1296.

[15] 杨广，吴晓平，常汉宝. 基于模糊灰色关联神经网络的综合故障诊断方法研究[J]. 武汉理工大学学报,2008,32(5):861-864. YANG Guang, WU Xiaoping, CHANG Hanbao. Research on Synthesized Fault Diagnosis Technique Based on Fuzzy Gray Relational Neural Network[J]. Journal of Wuhan University of Technology,2008,32(5):861-864.

[16] DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[17] 余志生. 汽车理论[M]. 北京：机械工业出版社，2007. YU Zhisheng. Automobile Theory[M]. Beijing: China Machine Press,2007.

(编辑袁兴玲)

AnalysisonHydraulicParametersofInterconnectedSuspensionsBasedonFuzzyGreyCorrelation

ZHOU Bing CHEN Yibin GENG Yuan REN Chengyuan

State Key Laboratory of Advanced Design and Manufacture for Vehicle Body， Hunan University, Changsha,410082

TU46

10.3969/j.issn.1004-132X.2017.19.001

2016-09-01

国家自然科学基金资助项目(51275162，51575167)；国家重点研发计划资助项目(2016YFB0100903-2)

周兵，男，1972年生。湖南大学机械与运载工程学院副教授、博士后研究人员。主要研究方向为车辆动力学及其控制、车辆结构分析与优化。陈逸彬(通信作者)，男，1989年生。湖南大学机械与运载工程学院硕士研究生。E-mail:cyb51446-3307@126.com。耿元，女，1989年生。湖南大学机械与运载工程学院硕士研究生。任程远，男，1990年生。湖南大学机械与运载工程学院硕士研究生。