SP(1,1)上伴随作用的实矩阵表示

付健丽，曹文胜



(1,1)上伴随作用的实矩阵表示

付健丽，曹文胜

（五邑大学 数学与计算科学学院，广东 江门 529020）

本文用类似文献[1]的方法，先得到的李代数的一组标准正交基. 利用此组标准正交基建立了的李代数的Cartan分解，根据具体的基和Cartan分解求出的李代数的李乘积，并由此得到了的李代数在李群上的伴随作用的实矩阵表示.

；李乘积；伴随作用

1 引言及预备知识

Adeboye 和Wei 在文献[1]中得到了复双曲空间上等距群的李代数的实数维、李基及相应的Cartan分解，并得到了的李代数上伴随作用的实矩阵表示. 本文在此基础上研究了四元数双曲空间维数为1的情况.

，

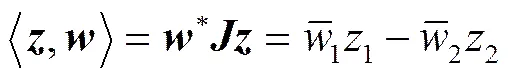
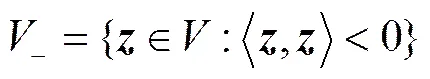
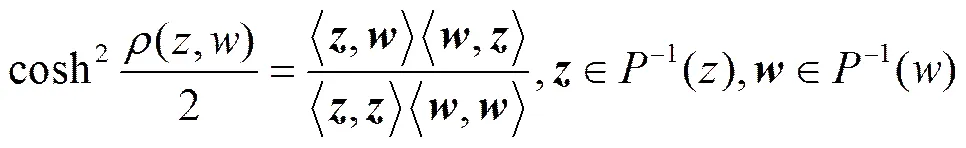
2 SP(1,1)上的李群、李代数问题

，

，

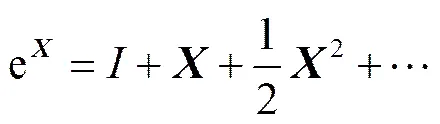
定义1 令

且令

.

，

，.

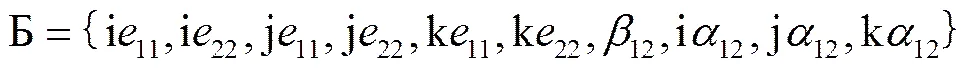
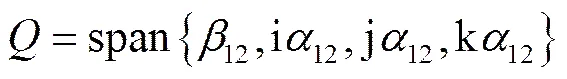
命题2

其中：

.

.

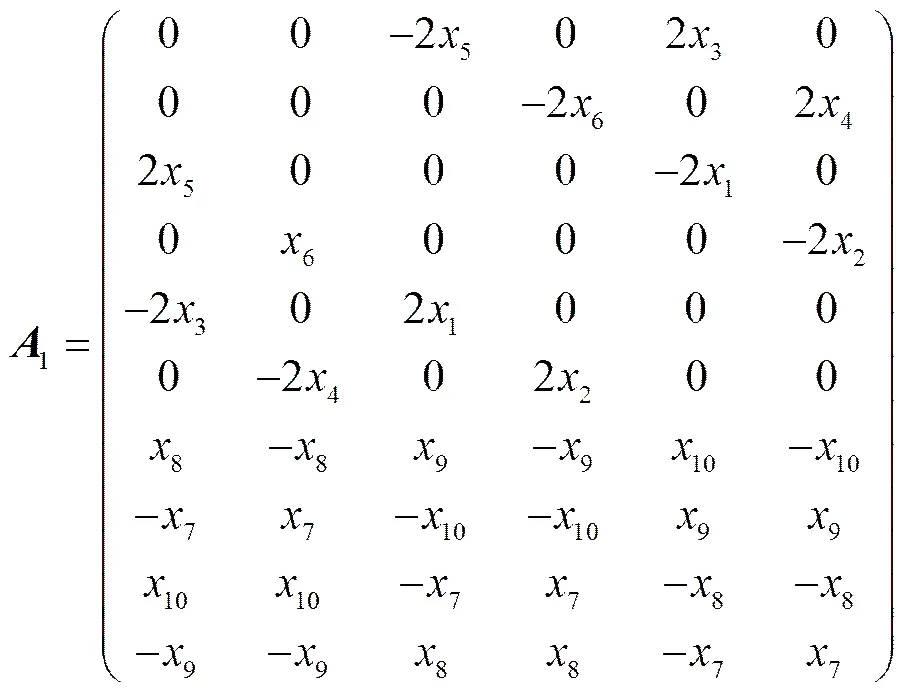
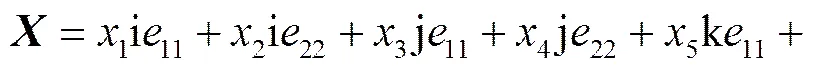
则由命题3有如下式子成立：

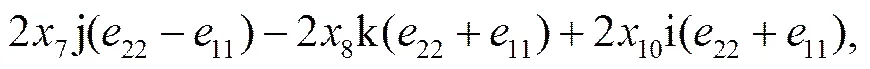
又因为

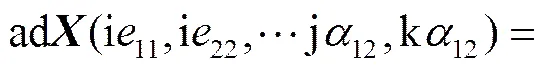
3 结论

由于复双曲空间可嵌入到四元数双曲空间，从方法论上说，复双曲几何的一些方法可借鉴到四元数双曲几何的研究中. 但由于四元数乘法的非交换性，四元数双曲几何的研究比复双曲几何的研究要困难得多. 本文在实数域上考虑四元数向量空间的相关问题，克服了这种困难，同时，本文的计算方法和结论可以推广到维四元数双曲空间上.

[1] ADEBOYE I, WEI G F. On volumes of hyperbolic hyperbolic orbifolds[J]. Algebraic Geometric Topology, 2012, 12(1): 215-233.

[2] ZHANG Fuzhen. Quaternions and matrices of quaternions [J]. Linear Algebra & Its Applications, 1997, 251(2): 21-57.

[3] PRUDHON N. K-theory for(,1) [J]. Journal of Functional Analysis, 2005, 221(1): 226-249.

[4] CAO Wensheng. Balls in quaternionic hyperbolic manifolds [J]. Kodai Mathematical Journal, 2016, 39(2): 439-454.

[5] GILMORE R, HERMANN R. Lie groups, Lie algebras, and some of their applications [J]. Physics Today, 1974, 27(11): 54-55.

[6] CAO Wensheng, PARKER J R. J{o}rgensen's inequality and collars in-dimensional quaternionic hyperbolic space [J]. Quart J Math, 2009, 62(3): 523-543.

[7] CAO Wensheng, GONGOPADHYAY K. Algebraic characterization of isometries of the complex and the quaternionic hyperbolic planes [J]. Geometriae Dedicata, 2012, 157(1):23-29.

[8] PARKER J R. Notes on complex hyperbolic geometry [M]. Cambridge: Cambridge University Press, 2003.

[9] GOLDMAN W M. Complex hyperbolic geometry [M]. Oxford: Oxford University Press, 1999.

[责任编辑：韦 韬]

Real Matrix Presentation of the Adjoint Action of(1,1)

FU Jian-li, CAO Wen-sheng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

In this paper, we obtain a set of orthonormal bases of theLie algebras by the method of Similar Literature [1] . We then use the set to establish the Cartan decomposition of theLie algebra. Finally, according to the specific bases and the Cartan decomposition, we obtain the Lie product of theLie algebra andthe real matrix presentation of the adjoint representation.

; Lie bracket product; adjoint representation

1006-7302（2017）03-0027-04

O151.21

A

2017-01-03

付健丽（1990—），女，广东清远人，在读硕士生，研究方向为复分析；曹文胜，教授，博士，硕士生导师，通信作者，研究方向为复分析.