一类微分多项式的零点的不等式估计

戴瑞芳，徐俊峰



一类微分多项式的零点的不等式估计

戴瑞芳，徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

本文利用精简计数函数给出了微分多项式的定量估计不等式，设为超越亚纯函数，为正整数，其中为的小函数满足.

亚纯函数；微分多项式；小函数；值分布

1 引言与定理

1995年，Bergweiler和Eremenko[2]证明了当时定理成立.

1993年，Chung等[3]猜测为超越亚纯函数，为正整数，取到任意非零有限值无限多次.

1998年，Zhang等[4]证明了以下结果：

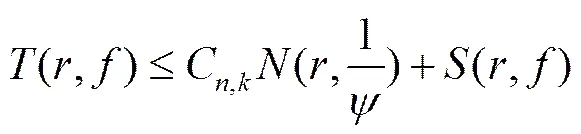
Alotaibi[6]将上述定量的计数函数改为更精确的精简计数函数，得到下述定量结果：

,

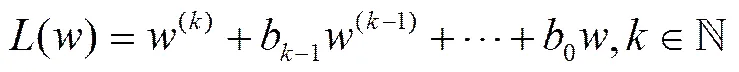
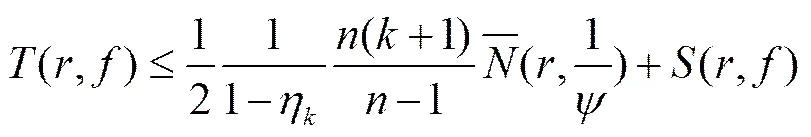
其中，

.

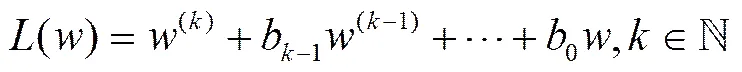
， （2）

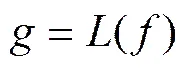
. （4）

.

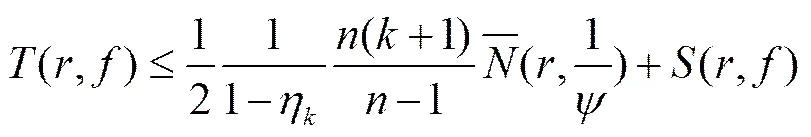
注2：最近Jiang[8]利用定理4的方法证明了如下结果：设为超越亚纯函数，均为的整数，为非零常数，我们可得：

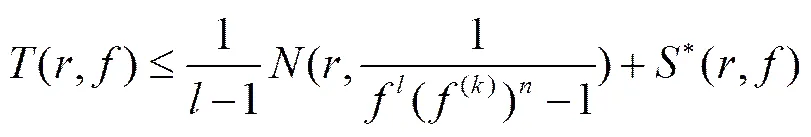
2 引理

本文定理6的证明需要用到以下引理

.

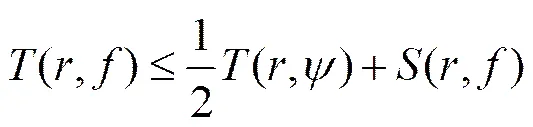
由式（1），（3）和（4）得

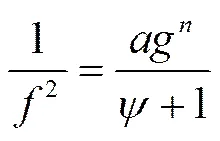
因此

所以

据此完成引理1的证明.

3 定理6的证明

.

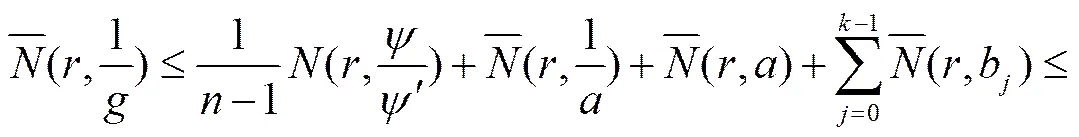
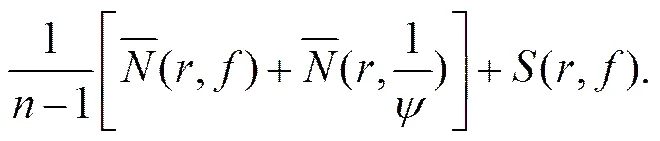
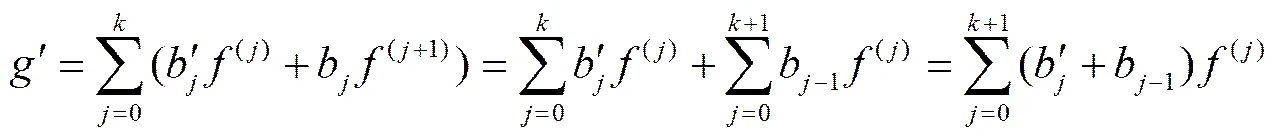
， （6）

其中

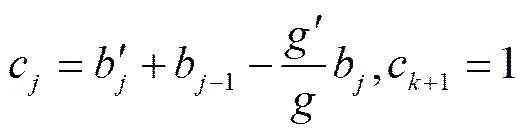
设

. （8）

对式（6）使用莱布尼兹法则得

， （9）

由式（7）得

，

及

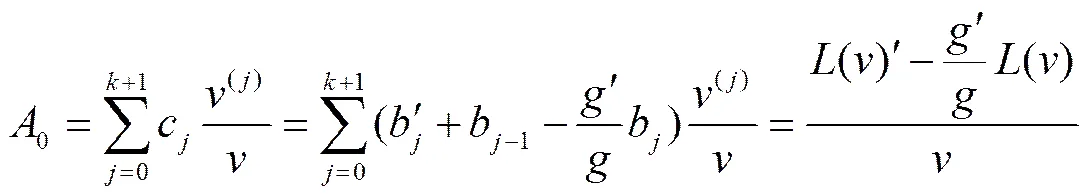
. （12）

我们分两种情形讨论：

，.

，.

，

，

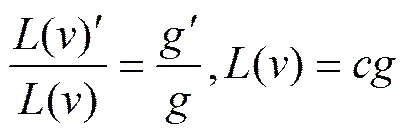
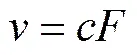
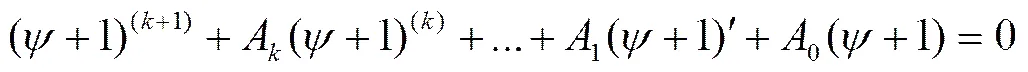
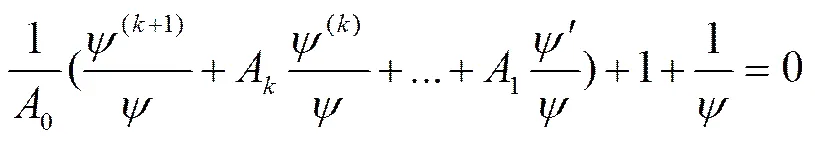
因此

由式（10）得

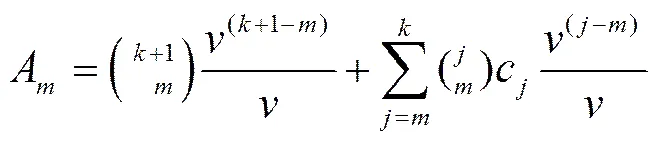
由式（5）得

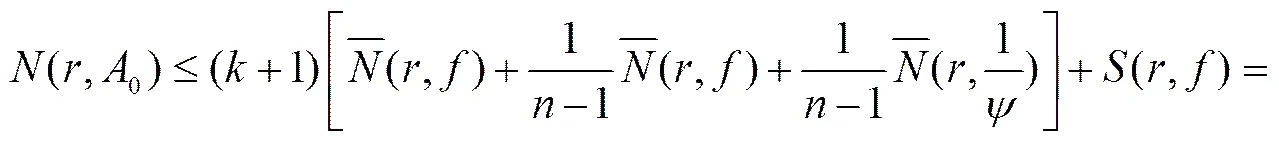
（14）

由式（1），（3）和（4）得

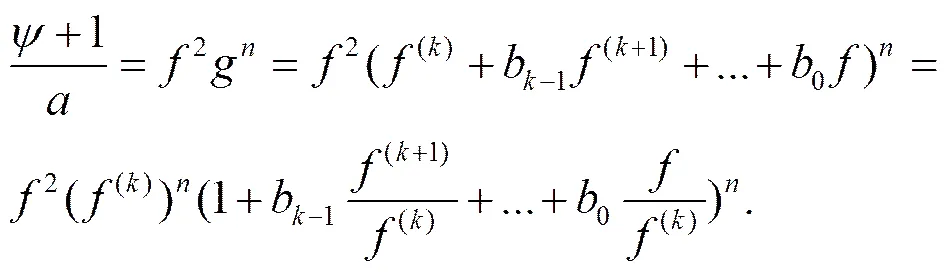
（15）

由式（14）和（15）得

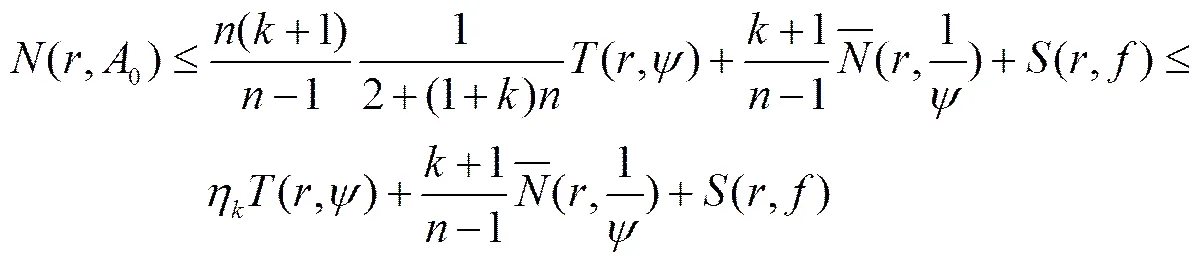
由式（10）和（13）得

, （17）

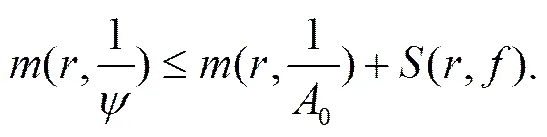
由式（16），（17）和（18）得

所以

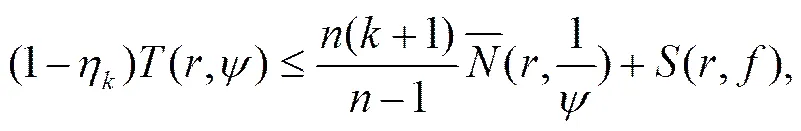
由引理1得

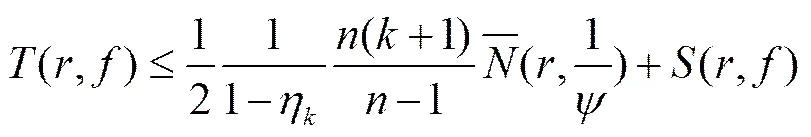
我们完成定理6的证明.

4 例子

[1] HAYMAN W. Picard values of meromorphic function and their derivati-ves [J]. Ann of Math, 1959, 70(2): 9-42.

[2] BERGWEILERAND W, EREMENKO A. On the singularities of the inverse to a meromorphic function of finite order [J]. Rev Mat Iberoamericana, 1995, 11: 355-373.

[3] YANG Chungchun, YANG Le, WANG Yuefei. On the zeros of[J]. Chinese Science Bulletin, 1993, 39(8): 2215-2218.

[4] ZHANG Zhongfa, SONG Cuodong. On the zeros of[J]. Chinese Ann Math Ser A, 1998, 19(2): 275-282.

[5] LI Ping, YANG Chungchun. On the value distribution of a certain type of differrential polynomials [J]. Mh Math, 1998, 125: 15-24.

[6] ALOTAIBI A. On the zeros offor[J]. Computational Methods and Function Theory, 2004, 4(1): 227-235.

[7] DOERINGER W. Exceptional values of differential polynomials[J]. Pacific J Math, 1982, 98(1): 1363-1364.

[8] JIANG Yan. A note on the value distribution offor[J]. Bull Korean Math Soc, 2016, 53(2): 365-371.

[9] XU Junfeng, YI Hongxun, ZHANG Zhanling. Some inequalities of differential polynomials II [J]. Mathematical Inequalities & Applications, 2011, 14(1): 93-100.

[10] HAYMAN W, MILES J. On the growth of a meromorphic function and its derivatives [J]. Complex Variables Theory Appl, 1989, 12(1-4): 245-260.

[责任编辑：韦 韬]

An Inequality Estimate of Differential Polynomials on the Zeros

DAIRui-fang, XUJun-feng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

In this paper, a quantitative estimate of the value distribution of the differential polynomialsis obtained by the reduced counting function, whereare positive integer,is the small function ofwhich satisfies.

meromorphic functions; differential polynomials; small functions; value distributions

1006-7302（2017）03-0001-07

0174.52

A

2017-03-09

广东省自然科学基金资助项目（2016A030313002）；广东高校优秀青年教师培养对象资助项目（Yq2013159）

戴瑞芳（1992—），女，广东新会人，在读硕士生，研究方向为复分析；徐俊峰，教授，博士，硕士生导师，通信作者，研究方向为复分析.