保持交换环上矩阵若干性质的映射
张国庭,赵显贵
保持交换环上矩阵若干性质的映射
张国庭,赵显贵
(惠州学院 数学系,广东 惠州 516007)
将域上的矩阵保持问题推广到交换环,有条件地得到了类似于域上的矩阵保持问题的若干结论,刻画了交换环上的矩阵空间中保持三类性质的映射:1)上三角矩阵空间的保持幂等的映射;2)全矩阵空间和上三角矩阵空间的保持对合的映射;3)全矩阵空间、上三角矩阵空间和对称矩阵空间的保持正交性的映射.
幂等矩阵;对合矩阵;正交矩阵;矩阵保持问题
矩阵的保持问题一直是一个活跃的研究领域,它主要研究在映射的作用下从某一矩阵到另一矩阵的某些性质的保持,具有广泛的应用背景,在微分方程、数理统计这些领域中具有重要的作用. 关于域上的矩阵的保持问题已取得了大量的研究成果[1-12]. 其中,文献[1]给出了域上的上三角矩阵空间的保持幂等的映射的形式;文献[2]刻画了域上全矩阵空间和上三角矩阵空间的保持对合的映射的形式;文献[3]研究了域上的矩阵空间的保持正交性的映射,分别刻画了全矩阵空间、上三角矩阵空间及对称矩阵空间的保持正交性的映射的形式. 本文研究交换环上的矩阵保持问题,推广了文献[1-3]的结论. 由于交换环中的元不一定可逆,本文的结论及其证明与文献[1-3]有所不同.
1 预备知识

定义1[1]201若满足,则称是上的上三角矩阵空间的保持幂等的映射.
定义2[2]539若满足,则称是上全矩阵空间的保持对合的映射. 将上述换成则称是上的上三角矩阵空间的保持对合的映射.
定义3[3]55若满足:,则称是上全矩阵空间的保持正交性的映射. 将上述换成则称是上的上三角矩阵空间(对称矩阵空间)的保持正交的映射.
2 上三角矩阵空间的保持幂等的映射
.
直接计算得:

.
直接计算得:

3 全矩阵空间的保持对合的映射

直接计算得:
. (3)
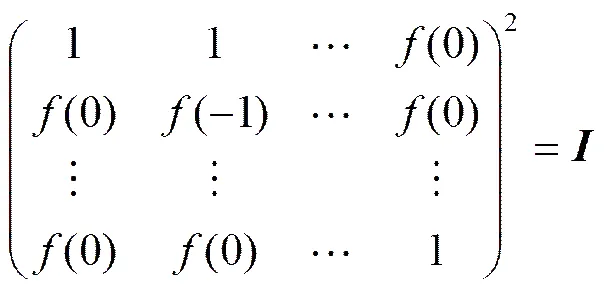
直接计算得:
. (4)

直接计算得:
. (5)

直接计算得:
. (6)
. (7)
由于2非零且不是零因子,于是由式(7)可得:

. (9)
下面的定理给出了交换环上的上三角矩阵空间的保持对合的映射的一种刻画.
证明 由定理2的证明可知充分性显然,下证必要性.


直接计算得:
. (10)
由于2非零且不是零因子,于是由式(10)可得:

.
直接计算得:

把式(11)代入式(12)得:
. (13)
4 全矩阵空间的保持正交性的映射

,
.
. (15)

. (16)

由式(16)得:
. (18)
从定理4的证明我们可以得到下面的定理.
下面我们研究对称矩阵空间的保持正交性的映射.
证明 由定理4的证明可知充分性显然,下证必要性.

. (19)

由式(19)和式(20)得:
. (21)
.

[1] 樊玉环,王佩臣. 域上上三角矩阵空间的保持幂等的函数[J]. 河北科技大学学报,2013, 34(3): 200-203.
[2] 樊玉环,马艳芬,蒋超凡. 域上保持对合矩阵的函数[J]. 河北科技大学学报,2014, 35(6): 538-542.
[3] 樊玉环,马晓峰,谭丽娟. 域上矩阵空间的保持正交性的函数[J]. 黑龙江大学学报(自然科学版),2015, 32(1): 54-57.
[4] 李嘉. 2×2矩阵空间上保幂等的线性算子[D]. 哈尔滨:哈尔滨工业大学,2007.
[5] 孟丽娜. 关于几类保持问题的研究[D]. 哈尔滨:哈尔滨工业大学,2007.
[6]GUAN Lijie, CAO Chongguang. Functions preserving square-zero matrices of orderover fields [C]// Proceeding of the Sixth International Conference of Matrix and Operators. Chengdu: World Academic Press, 2011: 216-218.
[7] 荣建英. 域上矩阵类保持问题[D]. 南京:南京航空航天大学,2006.
[8] 任苗苗. 几类保持半环上矩阵不变量的线性算子[D]. 西安:西北大学,2012.
[9] 王雪佳. 关于矩阵不变量的保持函数[D]. 哈尔滨:黑龙江大学,2013.
[10] 姚红梅,曹重光. 全矩阵空间保矩阵逆的加法映射[J]. 黑龙江大学学报(自然科学版),2008, 25(2): 225-228.
[11] 曹重光,皇甫明. 矩阵空间之间的保幂线性映射[J]. 数学研究与评论,2007, 27(2): 413-417.
[12] 关丽杰. 域上矩阵幂零及幂等性保持函数[D]. 哈尔滨:黑龙江大学,2012.
[责任编辑:熊玉涛]
Mappings That Preserve Properties of Matrices over Commutative Rings
ZHANGGuo-ting, ZHAOXian-gui
(Department of Mathematics, Huizhou University, Huizhou 516007, China)
We generalize preserving problems of matrices over fields to those over commutative rings and extend several existing results for matrices over fields. We characterize three classes of mappings that preserve certain properties of matrices over a commutative ring: 1) mappings preserving idempotence in upper triangular matrix spaces; 2) mappings preserving involution in full matrix spaces and upper triangular matrix spaces; 3) mappings preserving orthogonality in full matrix spaces, upper triangular matrix spaces, and symmetric matrix spaces.
idempotent matrices; involution matrices; orthogonal matrices; matrix-preserving problems
1006-7302(2017)03-0020-07
O151.21
A
2017-03-30
广东省自然科学基金资助项目(2016A030310099);惠州学院博士科研启动基金(2015JB021).
张国庭(1994—),男,广东广州人,在读本科生,研究方向为代数学;赵显贵,博士,通信作者,研究方向为代数学.

