带裂缝衬砌的应力强度因子分析
陈首超
带裂缝衬砌的应力强度因子分析
陈首超
(重庆交通大学 土木工程学院,重庆 400074)
在隧道工程中,二次衬砌的开裂严重影响着隧道结构的安全、耐久性以及隧道的正常运营. 本文为探究带裂缝衬砌的强度变化机理,基于断裂力学理论,将裂缝发展过程与应力强度因子关联,从理论计算和有限元模拟两个角度,总结了隧道衬砌裂缝发展与应力强度因子之间的一般规律.
衬砌;裂缝;应力强度因子
断裂力学源于对机械结构断裂现象的研究,从1957年提出至今,已经广泛运用在各类实际工程中. 如,向阳开等[1]运用概率断裂力学对由衬砌混凝土开裂导致的渗漏进行了分析;李治国等[2]在分析铁路隧道开裂状况及原因的基础上,利用断裂力学的方法研究了衬砌开裂隧道的稳定性,并提出了相应的裂缝治理技术;刘海京[3]基于断裂力学理论,分析了隧道衬砌的断裂模式,提出了带裂缝结构安全性的判定方法,建立了带裂缝的隧道结构模型以及其衬砌结构安全性的验算方法. 目前,我国正由公路建设高峰期逐渐转向养护期,各种不同程度的衬砌裂纹病害多有发生. 本文首先对复合荷载下带裂缝衬砌的应力强度因子进行理论计算,总结出弯压荷载下应力强度因子随裂缝深度延展的变化规律,然后运用有限元软件,对设计和带裂缝工况下的衬砌进行了同种工况下的数值计算,从另一个角度验证了应力强度因子随裂缝深度的变化规律.
1 断裂数值分析的理论基础
断裂力学常用于土建结构工程中的裂缝区域和结构破坏断裂参数的计算,从而评估结构的工作状态和发展趋势.
1.1 应力强度因子
线弹 性材料裂缝尖端处的应 力、应 变场表示如下:
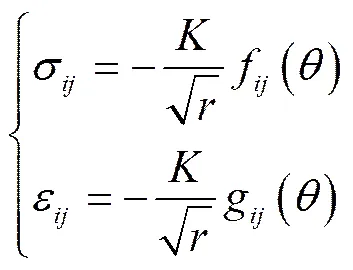
对于I型断裂,裂 缝尖端应力为:
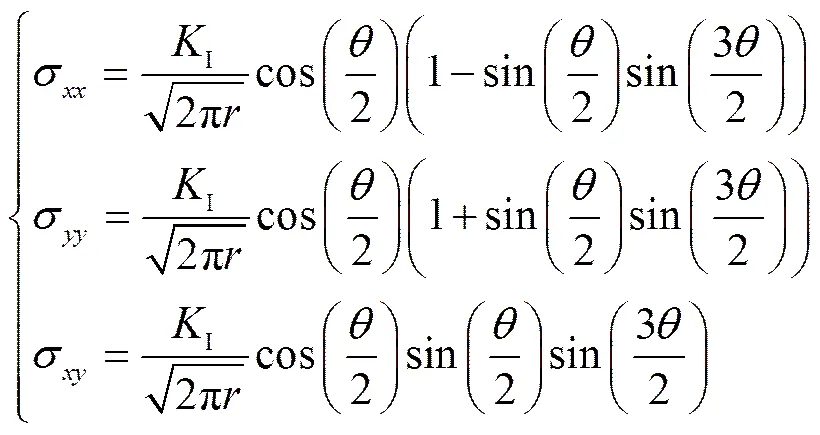
它是裂缝扩展单位长度(张开或收拢)所做功的度量,同时也是判断材料能量断裂的准则:当结构自身抗力不足以克服裂缝扩展所做功时,裂纹就会发展. 最初是由Griffith[4]提出,一般用于弹性材料,它与应力强度因子存在以下数学关系:
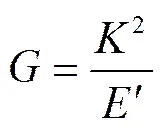
. (4)
裂缝尖端的应力、应变公式为:
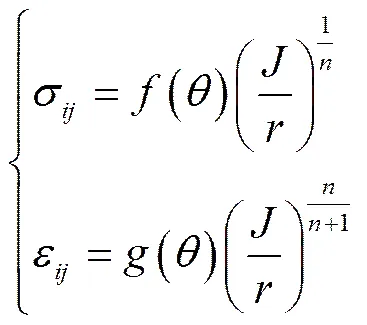
2 应力强度因子理论计算
2.1 纯弯曲的单边裂缝
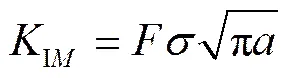
. (7)
表1 纯弯曲下的、值

表1 纯弯曲下的、值
裂缝深度a/cm0.20.50.81.02.03.0 F1.061.061.061.041.241.89 205.56312.65395.74446.65757.841 406.82
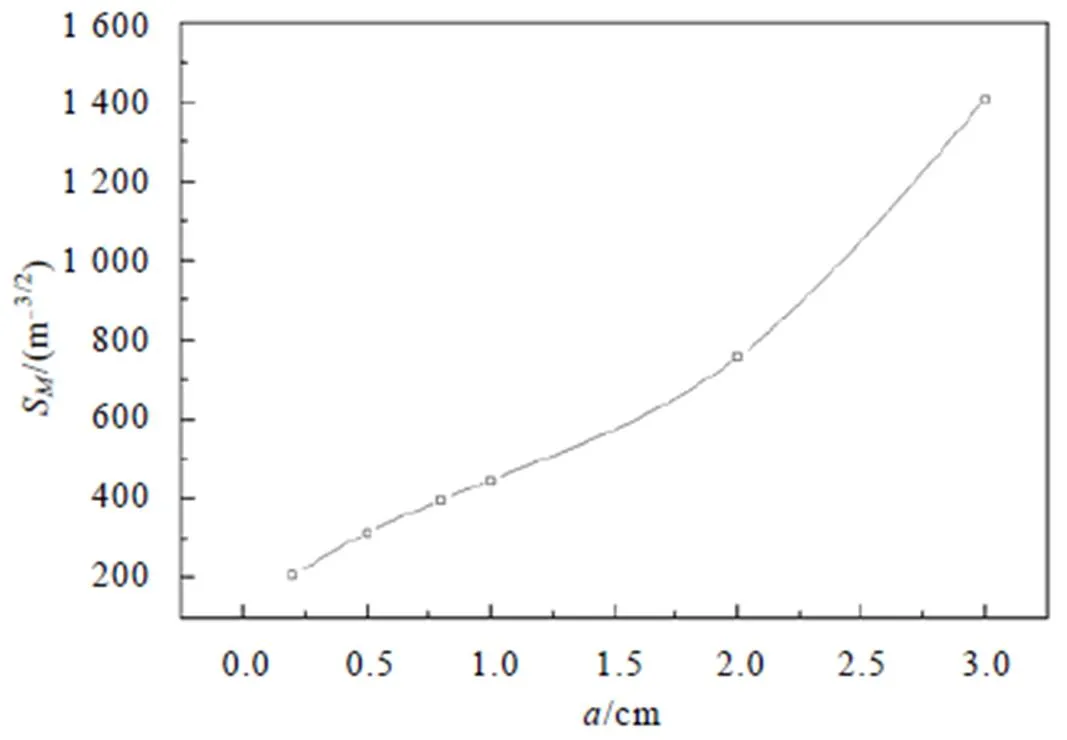
图1 裂纹深度与弯曲系数关系图
2.2 拉力作用下的单边裂缝
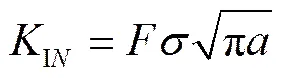
. (9)
表2 纯拉伸下的、值

表2 纯拉伸下的、值
裂缝深度a/cm0.20.50.81.02.03.0 F1.131.151.221.342.124.01 1.482.664.124.9610.5824.77
2.3 多因素条件下的计算

裂缝尺寸,时,由2.1和2.2计算结果推导出的结果,见表3.
表3 计算结果

表3 计算结果
裂缝深度a/cm 0.2 0.5 0.8 1.0 2.0 3.0
由表3,应力强度因子的发展在裂缝初期趋势平缓,但是随着裂缝的伸展,强度因子变化速率逐渐加快,当裂缝超过临界值后,即使是极其细微的延展,也会致使应力强度因子的突变,造成整个结构的破坏.
3 初始状态下二衬砌分析
3.1 有限元模型的建立
采用荷载结构法对二次衬砌在设计条件下进行安全分析,经统计,二衬裂缝大部分处于深埋段,围岩级别Ⅴ级,相关物理力学参数见表4.
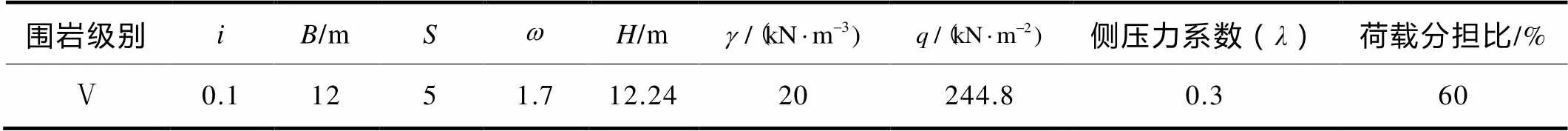
表4 V级围岩压力计算表
3.2 二次衬砌受力分析
根据《公路隧道设计规范》[6]规定,采用作为Ⅴ级围岩深埋段的二次衬砌的安全系数计算公式,其安全系数分布如图3所示.
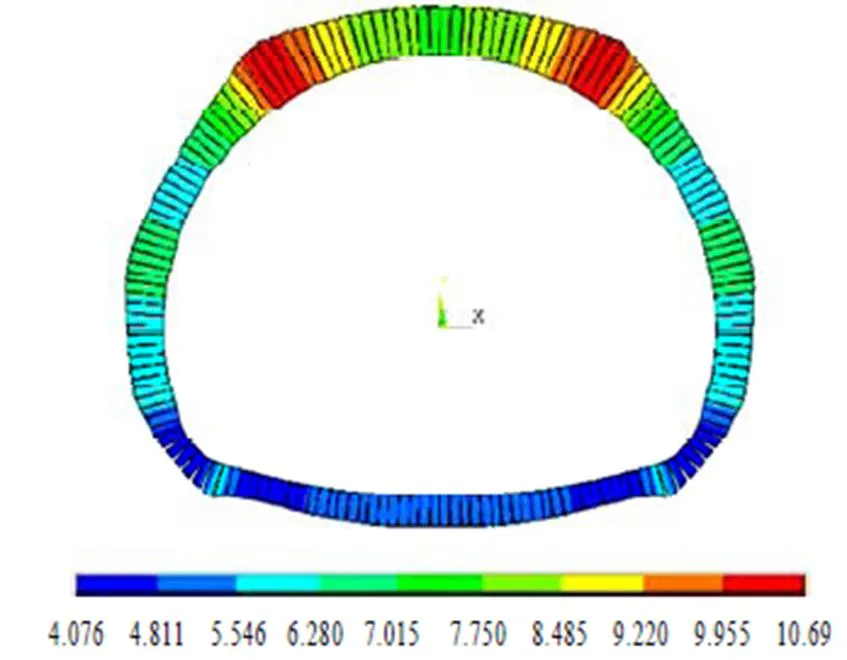
图3 安全系数分布图
由图3可知,该段围岩二次衬砌安全系数最小处为拱脚截面,衬砌的任一截面均处于受压状态,其安全系数均满足规范要求(不小于2.4),且从拱腰至边墙逐渐减小.
4 带裂缝二次衬砌分析
4.1 衬砌结构模型
4.2 有限元模型计算
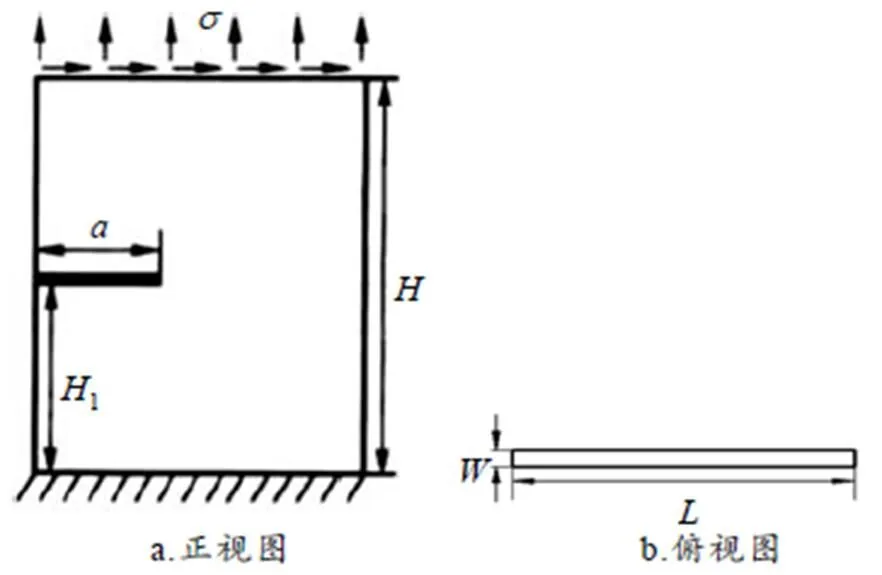
图4 三维裂纹力学模型
取荷载条件为不变值,改变裂缝深度进行有限元模拟. 在相同载荷作用下,当裂缝尺寸从发展到,裂缝尖端应力强度与端部所受应力的比值从4.52增长到13.72. 其中后的阶段,应力强度因子增长趋势明显加快,当裂纹继续增长,应力强度因子的改变将导致裂缝的突变,模型达到极限状态.
4.3 应力强度因子分析
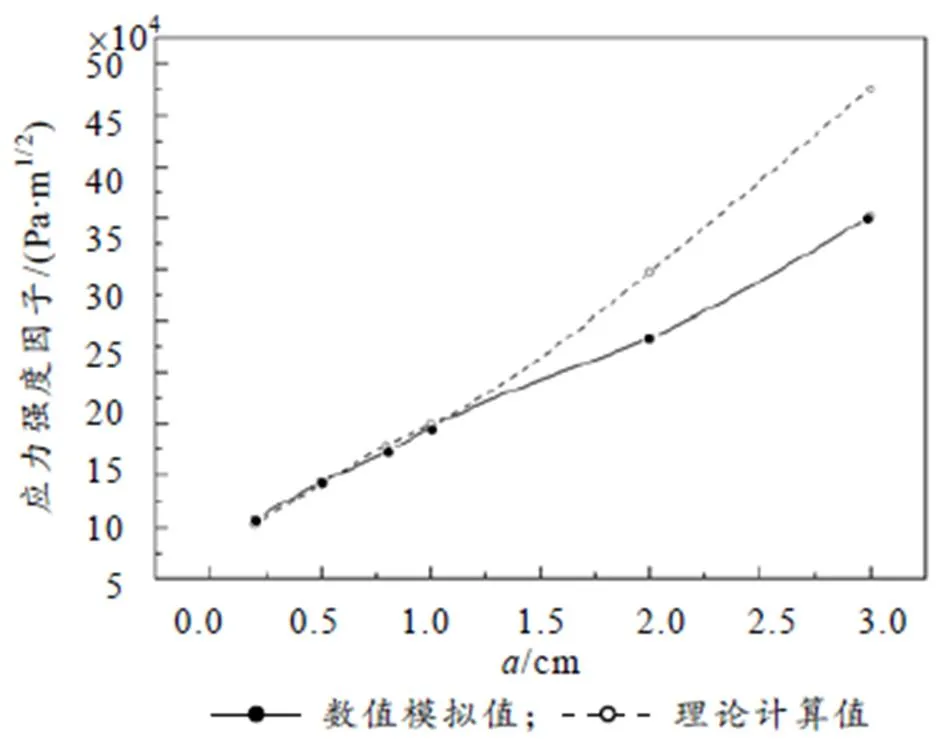
图5 裂缝深度与应力强度因子关系图
5 总结
基于断裂力学理论,将有限元模型计算结果与理论推导结果进行对比分析,可以得到以下结论:在衬砌裂缝发展初期,应力强度因子随裂缝增长的趋势是较迟缓的,这代表着初期阶段衬砌强度的损失对裂缝大小的敏感度是相对较低的;当裂缝发展到一定程度,裂缝的微量增长也会引起应力强度因子的突变,即代表着在裂缝发展的后期衬砌的强度损失对裂缝增长的敏感度是非常高的.
上述论断,从裂缝与结构强度之间的联系提醒了我们,在已建成营运的隧道养护工作中,对衬砌裂缝的及时修补是非常必要的,否则隧道结构的损伤速度将会随着裂缝的发展而加快,最终导致结构的失效. 但是,本文仅仅从弯、拉荷载两个角度分析了开裂衬砌的应力强度因子. 实际上,构件所受外力形式是多样的,基本形式就有弯曲、拉、压、剪切、扭转等,所以进一步结合更多的结构受力状态进行研究,更能真实反映带裂缝衬砌的实际状况.
[1] 蓝祥雨,向阳开,吴仕东,等. 新奥法隧道渗漏析因及预防[J]. 重庆建筑大学学报,2005, 27(5): 61-67.
[2] 李治国,张玉军. 衬砌开裂隧道的稳定性分析及治理技术[J]. 现代隧道技术,2004, 41(1): 26-31.
[3] 刘海京. 公路隧道健康诊断计算模型研究[D]. 上海:同济大学,2006.
[4] 洪起超. 工程断裂力学基础[M]. 上海:上海交通大学出版社,1987.
[5] 胥民尧. 断裂力学理论在公路隧道衬砌开裂中的应用研究[D]. 重庆:重庆交通大学,2008.
[6] 招商局重庆交通科研设计院. 公路隧道设计规范:JTG D70/2—2014[S]. 北京:人民交通出版社,2014.
[责任编辑:熊玉涛]
A Stress Intensity Factor Analysis of Lining with Cracks
CHENShou-chao
(School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China)
In tunnel engineering, the cracking of lining seriously affects the safety and durability of the tunnel structure and the normal operation of the tunnel. In order to explore the strength change mechanism of lining cracking, based on the fracture mechanics theory, this paper relates the development process of the cracks with stress intensity factors. It also sums up the general law between development of lining cracks and stress intensity factors.
lining; crack; stress intensity factors
1006-7302(2017)03-0073-06
U451+.4
A
2017-04-12
陈首超(1993—),男,重庆渝北人,在读硕士生,研究方向为隧道及地下工程理论.

