浅谈培养学生的问题意识

☉南京大学附属中学 杭丽华

浅谈培养学生的问题意识

☉南京大学附属中学 杭丽华

中学数学历经八次课程改革，到今天已走过了六十年.笔者从学生时代开始学习数学，到今天数学教学飞速的变革，数学教学逐步在向更高、更快的思维层面发展.但从一线教学的实际来看，笔者认为数学教学依旧没有彻底摆脱传统教学中的一个顽疾——教学中教师讲授部分过多.这样情况的出现还是有很多原因的，首先，作为中学数学教师的我们，当年学习的时候大都是在这样的讲授教学中度过的，本身缺乏主动对问题思考的意识，导致今天作为教师时也没有改变这样的意识.其次，教学课时的不足，这也导致了大量教学必须以精简、快速的节奏进行，在课堂教学中也压缩了学生思考的空间，更谈不上培养学生问题的意识.最后，学生的问题往往千奇百怪，若没有研究精神的教师往往招架不住，这也是专业化精神不足的体现.

数学学科课程改革对于学生的发展提出了全新的六大核心素养，要求教学进一步彻底向学生思维和能力发展的方向进行转变，各高校自主招生和三位一体的继续扩大也体现了学生能力要求凸显更为重要，因此培养学生思维和问题意识，比能机械模仿地解决数学问题来得更为重要，成为教学新的增长点.

一、注重情境，有感而问

中学数学是讲求形式化与非形式化的完美融合，只有两者的较好融合才能在教学中渗透知识的内涵和外延.教材中的知识是冰冷的、线性的、形式化的，这些形态特征决定了其不可能被学生很好地接受，因此教师的作用在于如何做好这些过渡，将其转换为学生通俗易懂的教育形态.笔者认为，中学数学中合理的转换需要借助情境，有情境才能让学生产生具体感知与抽象归纳之间的联系，才能产生一系列思考，产生问题，从而建立思考的意识，问题的意识.

案例1《指数函数》情境设计

师：前面同学们学习了指数运算，今天我们来学习指数函数.首先我们先来看一个实际问题，大家测量下，一张纸的厚度大概是多少？

生1：比较薄一点的纸，大概是0.01毫米.

师：请你对折一下，现在的厚度是多少？

生2：0.01×2毫米.

师：还是很薄！那我们接着对折，再对折，一直重复30次吧.你会想到什么？

生3：我很想知道，这个时候纸张的厚度是多少？

生4：我想知道它大概的高度有多少？

师：好！同学们都积极地提出了问题，至于结果如何？我们请其他同学思考.

生5：这个简单，应该是0.01×230毫米！我猜应该是三、四层楼这么高吧？

师：同学们列出的式子非常正确！至于这个数值到底是多大，猜测得对不对？我们不妨请大家用计算器算一算.

生6：0.01×230≈10737418（mm）≈10737.418（米）！这个数值很大，大到有点夸张！

师：是的！同学们一定很惊讶，一张很薄的纸对折30次的厚度竟然远远超过了珠穆朗玛峰的高度！

生7：是的！远比我们想象的要大得多的多！

师：那你对这个现象进一步想一想，你会觉得上述什么方面很值得进一步的思考？

生8：我想知道为什么2n增加得这么快？这难道就是今天要学的一种新的函数？这样的增长速度让我想起了生物学中常常讲起的细胞分裂，1个变2个，2个变4个，4个变8个，…，如此下去，爆炸式的增长.

师：同学们的思维非常灵活，也提出了很多的问题，这正是我们今天要研究的一种新的基本初等函数——指数函数，即形如f（x）=ax（a＞0anda≠1）的函数.

本课例的引入是生活中的折纸问题，一个小小的、不起眼的折纸问题，引发了学生积极的思考，而且折纸30次这种实践让学生对课堂充满了期待，学生非常渴望知道0.01×230毫米到底是一个多大的数量概念？当这一答案揭晓的时候，学生又提出了问题：为什么增加如此之快？这些都与本课成功的情境设置精密相关，因此可以说一个合理的情境可以激发学生思维的迸发，爆发出一系列迫切的问题，是一种潜意识的问题思考.

二、以错为媒，自发而问

数学离不开解题，而解题水平的提升离不开错误的发生.可以这么说，一定程度上的合理错误是提升学生思考全面性的必经之路.要提升学生的自我思考、提出问题意识，可以从错误的试题中寻求答案，这种寻找恰恰反映了学生学习的障碍所在，对学生思维严密性有着较强的反馈，这可以大大激发学生后续学习的步骤，即发现问题、解决问题、提出问题，从而形成一种自发而问的问题意识.

案例2已知f（x）=ax2+cx，且1≤f（1）≤3，-1≤f（-1）≤1，求f（2）的取值范围.

①+②，得0≤2x≤4，即0≤4x≤8；

②×（-1），得-1≤y-x≤1.③

①+③，得0≤2y≤4.

故而代入f（2）=4x+2y，得0≤f（2）≤12.

分析：本题是不等式与不等关系章节学习中的一个经典问题，这种错误也是初学者易犯的错误.教师请学生自我验证，并自行发现问题、解决问题，提高学生自发而问的意识.

师：请同学们检验下，你的答案正确与否？

生1：我发现有些问题，由0≤x≤2以及0≤y≤2得到0≤x+y≤4，这与已知条件相矛盾啊！

生2：是的！但是我在上述过程中，好像没发现什么问题？

师：那先从结论出发思考下，明明1≤x+y≤3，怎么经过一变形再回来，就变成0≤x+y≤4了呢？从这里入手思考应该有收获？

生3：我画了一幅图，从图中我明白了为什么这么做是不行的！

师：展示给大家看一看，再说说理由.

图1

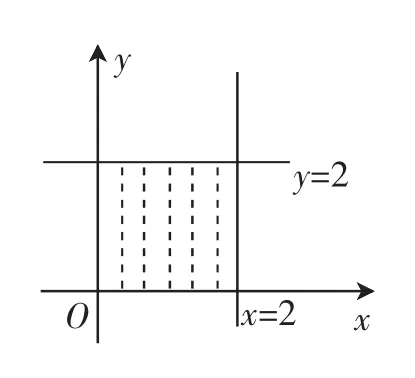
图2

我发现，题中条件所表示的变量范围远远小于变形之后的变量范围，说明在研究过程中，已经将变量范围给扩大了，这样势必导致前后矛盾的产生！

生4：我认为，这主要是变量x、y之间有相互制约的关系，而得到0≤x≤2以及0≤y≤2时，我们已经破坏了两者之间的相互制约，导致了范围的扩大，这里图形比较好地阐述了错误的原因.

生5：哦，我明白了！也就是说，得到的单量0≤x≤2以及0≤y≤2的范围并没有错，但是它们之间的相互制约性却没有办法显现出来，并不是说0≤x≤2以及0≤y≤2所有的点（x，y）都满足题中条件，因此错解就是错在这里了.

生6：正确的解答：f（2）=4x+2y=3f（1）+f（-1），由已知可得3≤3f（1）≤9，-1≤f（-1）≤1，故而两式相加可得2≤f（2）≤10.

师：本题也可以用我们后续线性规划的知识求解.

典型的错误是一个合理的教学平台，恰恰可以让学生进行深思和问题意识的培养.本题中的不等关系，是初学者常常犯的错误之一，从教学中不难发现教师哪怕讲数遍，学生依旧在这里不停的犯错误，究其原因是那是教师的思考，并不是学生的思考.所以，以错题为载体，请学生探索和发现，将这一错误挖掘的过程不断的分析、思考，用学生相互思考、提问的方式获得了成功.

三、以变为链，深思而问

数学最终离不开解题，那么在解题中带来的将是更多的思考，而思考带来的是思维的深入，有了深入的思维才会有不断发现问题、思考问题的意识.

案例3 AB是平面α外固定的斜线段，B为斜足.若点C在平面α内运动，且∠CAB等于直线AB与平面α所成的角，则动点C的轨迹为___________（填圆锥曲线中的某一种）.（答案：抛物线）

分析：这样的问题到底是从哪里去思考切入？考查了什么知识点？后续学习中更要关注什么？如何真正理解以教材为本的教学？……其实，教材圆锥曲线一章的章头图中，清晰地表述了圆锥曲线之所以这样称呼的主要原因，即用平面截圆锥曲线得到的截口曲线.这样的教学让学生获得了思考和问题：

问题1：圆锥曲线为什么这么称呼？

问题2：截口曲线有哪几种？

问题3：学习要注重什么？要注重教材中基本概念以及延伸.

变式1：斜线段AB与平面α所成的角为60°，B为斜足，平面上的动点P满足∠PAB=30°，则点P的轨迹是___________.（答案：椭圆）

变式2：二面角α-l-β的大小为120°，AB垂直平面β交l于B，动点C满足AC与AB成40°角，则点C在平面α和平面β上的轨迹分别是___________.（答案：双曲线、圆）

知识的变式链接，是知识深度使用的体现，这种体现的背后挖掘了学生积极思考知识的本质，从而从更深的概念角度提高了问题的意识，获得了更好的学习体验.总之，培养学生的问题意识还需要全方位的教学引导，教师要有意识的引导、设计，就能从多角度去提升学生的问题意识，获取更好的知识本质.

1.赵绪昌.让数学课堂教学的错误美丽起来［J］.中国数学教育（高中版），2011（1）.

2.王甫森.学会提问——课堂教学实践及反思.［J］.中国数学教育（高中版），2011（10）.