用导数开拓解题新天地——例谈导数在解题中的应用

☉安徽省六安中学 张本春

用导数开拓解题新天地
——例谈导数在解题中的应用

☉安徽省六安中学 张本春

高中数学题型较多，一些题型采用传统的解题方法来解题时，不仅计算烦琐，而且解题难度较大，需要花费一定的时间才能得出正确答案，而运用导数来解题，往往能够迅速找到解题突破口，收到事半功倍的效果.因此，教学实践中，教师应注重培养学生运用导数解答数学题目的意识，并在日常教学中讲解相关例题，使学生掌握应用导数解题的方法与技巧.

一、从陌生到熟悉，搭建转换桥梁，解决线性规划问题

学生对高中数学中线性规划题目并不陌生，他们在各类测试中经常会遇到此类题目，这类题目的难度一般不大.不过，线性规划与函数结合在一起后，题目的难度便会大大增加，这也给学生的数学能力提出了较高的要求.学生经常要将给出的已知条件进行转化，此时就会涉及导数知识的灵活应用.譬如，利用导数相关知识，将给出的复杂条件转化为比较熟悉的约束公式，然后再解题，直至将题目顺利解答出来.

分析：题目与学生较为常见的线性规划题目有所不同，其与函数进行巧妙的融合，试题难度提高了一个水平，导致部分学生因不会转化，而无法进行解答.其实借助导数将不熟悉的公式转化为熟悉的公式，不难进行求解，解题步骤如下：

根据题意，g′（x）=x2+ax-b≤0在 x∈［-1，3］ 上 恒 成 立 ，即代入得在此基础上求a2+b2的最小值，学生较为熟悉，根据求出的约束条件，画出可行域，如图1所示.

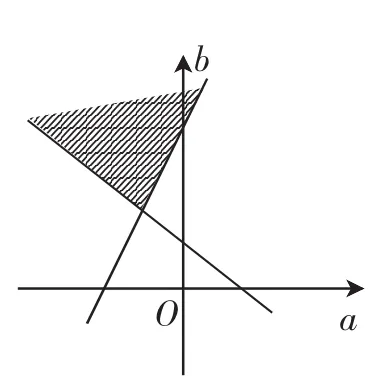
图1

a2+b2可看做可行域中的点至原点距离的平方，两个直线的交点与原点的距离最短，由图不难得出交点坐标a=-2、b=3，此时a2+b2=13.

二、注重知识融合，学会化繁为简，解决最值问题

圆锥曲线是高中数学教学的重点、难点，因圆锥曲线经常涉及复杂的计算，而且许多计算都具有一定的技巧性，因此，很多学生在学习圆锥曲线知识时，都感觉到吃力.在学习中，面对复杂的圆锥曲线类型的题目，许多人经常是不知所措.在各类圆锥曲线题型中，求最值问题较为典型，采用传统的计算方法固然能够求值，但计算烦琐，容易出错，而应用导数进行求解，不仅能提高解题效率，还能提高解题的正确率.因此，日常教学活动中，教师应注重导数在解析几何相关题型中的应用，培养学生应用导数解答解析几何题目的意识.

例2 已知抛物线方程为y=x2-2x-1，选取其上的一点，使其与原点的距离最短，并求出其最小值.

分析：解答该题目时，可设出抛物线上任意一点，而后利用两点之间的距离公式及导数知识进行求解，计算过程中应多加谨慎，确保计算的正确性，具体解答步骤如下：

假设抛物线y=x2-2x-1上任意一点m（x，y），其与原点之间的距离，设（fx）=x2+（x2-2x-1）2=x4-4x3+3x2+4x+1，那么f′（x）=4x2-12x2+6x+4，当f（′x）=0，即0时，其根分别为

f′（x）、f（x）随x的变化情况，如下表：

x （-∞，x1） x1 （x1，x2） x2 （x2，x3） x3（x3，+∞）f′（x）0+-0+f（x）↘极小值↗ 极大值↘ 极小值↗

三、构造新的函数，利用分类讨论，证明不等式问题

不等式题目在高中数学中较为常见，不等式具有一定的抽象性，很多学生面对不等式时都不知道如何下手.其实，我们可以将不等式题目进行归类，将其分为能成立和恒成立两类.然后，运用导数进行解答，确切来说是采用转化法或构造法来解析不等式.其中转化法指通过转化将其转化为容易证明的不等式.例如，将含有lnx、ex的式子转为二次函数或一次函数的式子，利用最值及单调性进行解答.构造法指通过移项构造一个新的函数，利用函数的最值和单调性进行求解.

例3已知函数f（x）=ln（1+x），g（x）=kx（k∈R）.

（1）当x＞0时，证明：f（x）＜x；

（2）当k＜1时，存在x0＞0，使得对任意的x∈（0，x0），f（x）＞g（x）恒成立.

分析：（1）对要证明的问题进行转化，即f（x）-x＜0在x＞0上恒成立.而后采用导数对转化后的函数单调性进行判断，不难解答，证明步骤如下：

（2）同样需要在已知条件的基础上，进行转化构造新的函数，进行分类讨论不难进行证明，具体证明步骤如下：

令h（x）=f（x）-g（x）=ln（1+x）-kx，x∈（0，+∞），那么，显然当k≤0时，h′（x）＞0成立，即h（x）为单调递增函数，h（x）＞h（0）=0，符合题意要求.当0＜k＜1时，h′（x）=0，可得，当时，则h′（x）＞0对x∈（0，x0）恒成立，因此，h（x）在x0＞0上单调递增，即h（x）＞h（0），不难证明.

四、借助导数思想，简化解题思路，解决数列求和问题

数列是高中数学的难点，在数列求和相关题目时，我们常用求和公式来解题，不过这种解题方法过程烦琐，稍有不慎就会出错.当学习导数相关内容后，教师可引导学生利用导数知识解答数列求和相关题目.实践表明，采用导数求解数列的和，计算过程较为简单，很容易得出正确结果，有例子为证：

当x≠0且x≠1，n∈N*时，1+2x+3x2+4x3+…+nxn-1=（1+，采用导数思想求解数列前n项和问题，能大大简化计算步骤，而且计算准确性高，因此，教学实践中，教师应注重相关题型的讲解，使学生充分感受应用导数解题的便捷性.

例4 已知数列｛an｝满足an+2=qan，其中q为实数，且q≠1，n∈N*，a1=1，a2=2，且a2+a3，a3+a4，a4+a5是等差数列.

（1）求q和｛an｝的通项公式.

分 析 ：（1） 根 据 已 知 条 件 不 难 求 出q=2，an=

（2）求解出q与｛an｝的通项公式，应用导数知识，不难进行求解.由以上可得，设｛b｝的前n项和为S，构nn造函数f（x）=x+x2+…+xn.

五、化抽象为具体，建立数学模型，解决生活实际问题

高中数学中有许多与生活实际相关的题目，此类题目大多是要求学生利用所学进行解答，如用料最少、效率最高、路程最短等问题.通过对这些题型进行分析可以发现，将这些实际问题转化为利用导数求极值问题，是一条解题捷径.为保证学生顺利解答出此种类型的题目，一般情况下应按照以下思路进行求解：首先，认真读题，根据题意抽象出相关的数学模型，列出相关的函数关系式.需要注意的是，为保证结果的正确性，我们要充分考虑实际情况，对定义域作出限制和约束.其次，利用导数求解出函数的最值.最后，解答结果，并考虑实际情况进行合理取舍，保证最后结果的正确性.

图2

例5 如图2所示，直线l1、l2为相互垂直的两条公路，曲线C为一湖泊的边缘，现在拟沿着湖泊边缘修建一条连接l1、l2的公路l，其中M、N为曲线C上的两点，距离l1、l2

的距离分别为5km、40km，20km、2.5km，以l2、l1为x、y轴建立直角坐标系xOy，曲线C满足函数a，b为常数）.

（1）a、b的值分别是多少？

（2）如果公路l和曲线C在P点相切，设P点的横坐标为t，求公路l的函数解析式；t取何值时公路l的长度最短，最短长度为多少.

分析：（1）题目中给出了M、N两点的坐标及曲线C的函数关系式，分别代入不难求解，a=1000，b=0，即y=

（2）要求公路l的直线方程，题目给出了P点的横坐标为t，由此不难求出P点的总坐标.根据（1）求得的曲线C方程，可求出其在P点的导数，由此不难得出公路l的直线方程为，其中t∈［5，20］.题目中要求直线l的长度最短，此时设，求导得，由h（′t）=0得h（t）、h′（t）随t变化情况如下表所示：

t （5，10 2 ） 10 2 （10 2 ，20）h′（t）-0+h（t） ↘ 极小值 ↗

六、结论

由上述可知，导数在解答相关题型时有着显著的优势.因此，在数学教学实践中，教师应注重导数在解答数学题目中的应用，帮助学生深刻理解导数知识.同时，通过典型例题讲解和导数的灵活运用，使学生掌握应用导数求解数学问题的方法与技巧，激发学生的创造性思维，提高学生的解题能力和解题正确率.

1.李明.高考导数试题分析及教学策略研究［D］.苏州大学，2016.

2.华燕萍.高中生“导数及其应用”学习中的常见错误分析及教学对策研究［D］.上海师范大学，2014.

3.李亚青.基于学生导数理解障碍的教学设计研究［D］.四川师范大学，2015.F