重力梯度张量种植反演
曹书锦,朱自强,鲁光银
重力梯度张量种植反演
曹书锦1, 2, 3,朱自强2,鲁光银2
(1. 湖南科技大学页岩气资源利用湖南重点实验室,湘潭 411201;2. 中南大学地球科学与信息物理学院,长沙 410083;3. 湖南科技大学资源环境与安全工程学院,湘潭 411201)
针对在重力梯度张量正演中计算耗时过长和核矩阵内存消耗过大等制约反演实施的瓶颈问题,在L1范数的基础上,引入种植反演,用累加求和分析替换迭代求解,避免计算或存储反演核矩阵,以减少内存占用和加快反演迭代;针对种植反演容易导致相邻异常源相互侵入的问题,引入一个基于位场水平衰减特性加权函数来限制密度吸引子的作用范围,以期使密度吸引子忽略较远的异常源,抑制相邻异常源相互干扰。反演结果及分析表明重力及重力梯度张量种植反演所需计算机内存小和水平衰减特性加权函数能有效的抑制相邻异常源的 侵入。
种植反演;水平加权特性函数;重力梯度张量;L1范数
对于位场反演而言,正演计算是其重要组成部分,正演计算精确性和计算效率是主要制约反演充分发挥作用的瓶颈问题[1−4],尤其在大尺度/海量位场数据的反演解释中,这种瓶颈效应更为明显[5]。针对在重力场中正演计算耗时过长、核矩阵内存消耗过大等制约重磁反演的瓶颈问题,很多学者自正反演两个方面开展富有成效的研究。在正演研究中,1) 在不改变计算量的前提下,开展高性能计算[1],但由于不储存核矩阵,在实际应用中,每次反演迭代都涉及到多次正演计算,导致其应用于反演计算的效率相对较低,同时其硬件和软件的准入门槛较高,导致研究成果不多;2) 采用压缩技术,以降低核矩阵的存储成本,如等效构架技术[3]和小波压缩技术[6]等,其在减少核矩阵的所需存储空间的同时,能极大的提高正演计算速度,但等效构架技术不适用带地形观测数据,小波压缩技术在一定程度上损失了信号精度[1]。在反演研究中,1) 引入预条件技术,以优化系数矩阵的条件数,加快反演迭代的进行[7];2) 引入密度上下界函数,以加快重构密度向密度上下界附近靠拢,加快反演收敛速 度[8−10];3) 引入新的反演方法,以规避反演核矩阵的存储或计算,如逆时偏移技术[11−12]、小波变换技术[6]和足印反演[13]等。
基于以上考虑,在L1范数的基础上[14],引入种植反演,以累加求和分析替换最优化问题中的迭代求解,减少每次参与反演迭代的物性网格的个数,避免计算或存储反演核矩阵,以减少内存占用和加快反演迭代;针对在L1范数下的重力及重力梯度张量种植反演易于导致相邻异常源相互侵入的问题,通过引入加权函数,使密度吸引子或种子忽略较远的异常源,减弱相邻异常源相互侵入的趋势。反演结果及分析表明重力及重力梯度张量种植反演所需计算机内存小和水平衰减特性加权函数能有效的抑制相邻异常源的侵入。
1 重力梯度张量种植反演
为引入种植反演,首先假设为实际观测数据,为相对应的预测模型通过正演得到的预测数据,此处构建一个残差向量:
=−
由基于最小二乘估计定义的数据泛函可知:

式中:下标对应于各观测点;为观测点个数。
相比于L2范数,L1范数不敏感于含大误差的数据,能提供稳健的估计策略[15]。

传统反演应用正则化方法降低地球物理反问题中解的不稳定性和非唯一性,而在种植反演中,为使原有病态问题转化为良态,引入如下约束[16−18]:
1) 紧致或聚焦,以确保在反演所得密度模型中没有空洞;
2) 仅以种植反演算法中所提供的密度吸引子为中心逐步选择最优网格,且最优网格的密度值与相邻的密度吸引子密度相同,即=;
3) 对于其他未涉及的网格,强制密度值等于零。
基于以上约束策略,可以构建种植反演的目标 函数:
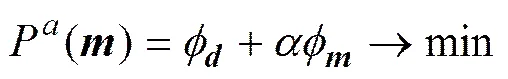
(3)
针对种植反演中密度吸引子的水平位置不易确定及邻域网格没有空间范围的限制,导致相邻重构异常源易于相互侵入等问题,UIEDA等[18]提出利用位场数据中的水平形态特性(“Shape-of-anomaly” data misfit)来确定异常源的水平空间分布,以确保在异常响应幅值大的区域,优先更新物性网格,在式(1)的基础上,数据泛函可重新定义为
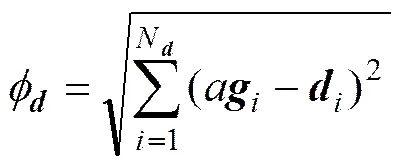
式中:为缩放因子,对于任意给定预测数据,可通过变换上式计算:
但式(4)主要关注预测数据和观测数据峰值间的差异,而并没有考虑异常响应幅值较小的区域如:深部/弱异常源等,同时在重力梯度张量多分量联合反演中,虽然可以使用多个缩放因子进行联合反演,但没有考虑重力梯度张量分量在深度方向及水平方向的衰减特性,即重力梯度张量各分量的缩放因子趋势并不一致,当g分量处于峰值时,而g分量却趋于零。因而在对深部/弱等异常源反演时存在一定的缺陷。
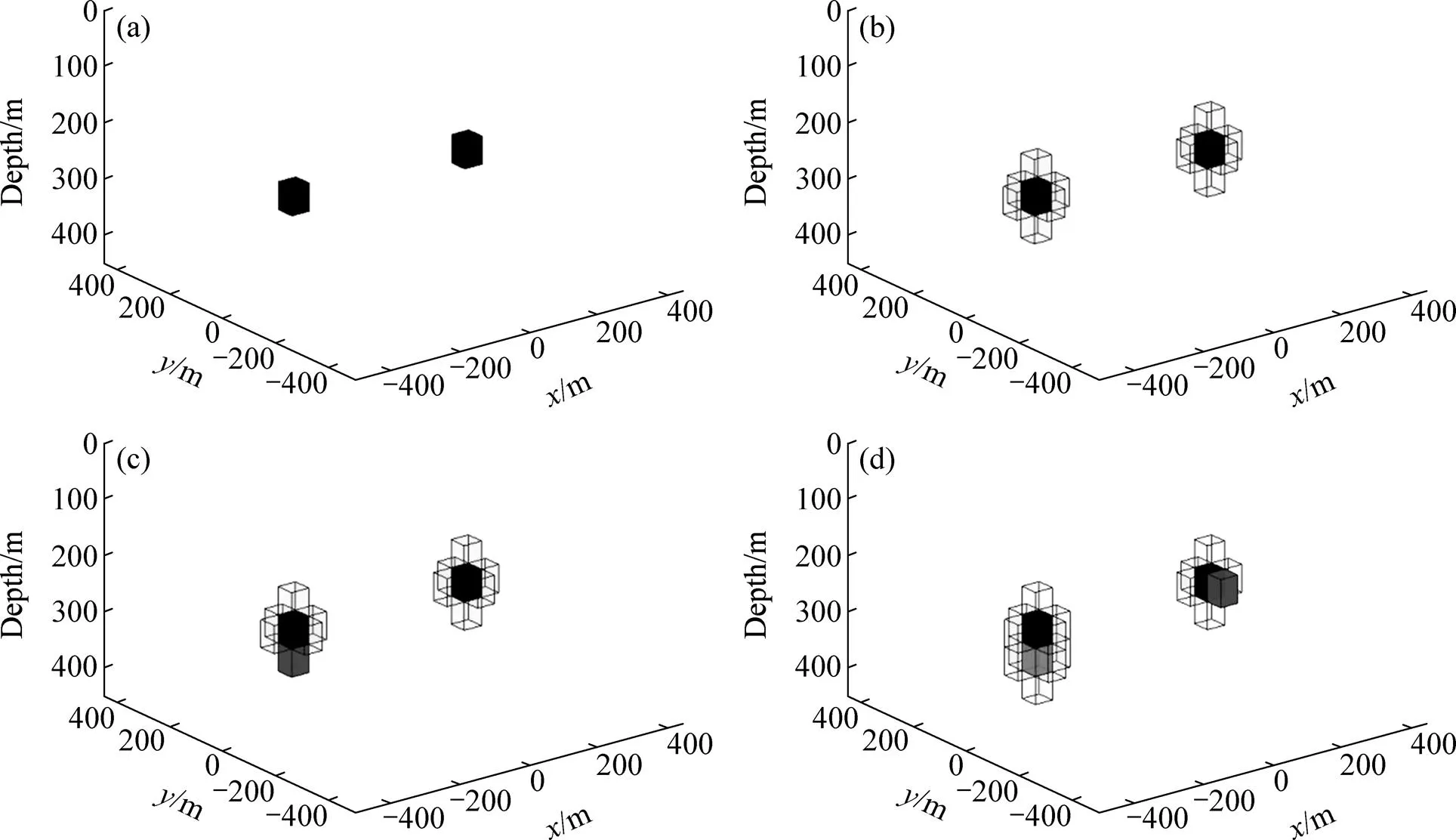
图1 种植反演算法的4个阶段
与传统反演基于迭代更新不同,种植反演算法主要通过选取与密度吸引子相邻的最优网格单元,并更新该网格单元密度,以实现反演迭代。以图1为例,来阐述种植算法的计算流程。
图1所示为种植反演算法的4个阶段。1) 初始化,首先设置两个密度吸引子(黑色的网格单元),并确定其空间位置及密度值,密度吸引子的空间位置可根据欧拉反褶积给出,密度值依赖于人工经验选择;2) 构建邻域网格,确定与两个密度吸引子相邻的物性网格单元(浅绿色);3) 遴选最优网格,确保逐步变小和确保P()泛函逐步减小的前提下,确定最优网格单元(蓝色),并赋予该网格与密度吸引子相同的密度值,将其自邻域网格选集中剔除,将这一过程定义为最优网格选择策略。4) 进入下一次迭代,选择其他密度吸引子,在其相应的邻域网格中,利用最优网格选择策略选择最优网格单元,并赋予该网格与密度吸引子相同的密度值(即红色网格)。种植算法遍历所有密度吸引子及所有的网格以满足反演终止条件。
2 算法验证
图2所示为正演模型Ⅰ及其不同方法的反演效果对比。如图2(a)所示,构建含有2个同深度异常体的模型对上述方法原理进行对比分析与验证。2个异常体的长×宽×高均为200 m×200 m×200 m,异常体顶板埋深均为200 m,底板埋深均为400 m,剩余密度均为1.0 g/cm3。将场源空间划分为20×20× 10=4000个单元格,每个单元格沿、和轴方向的长度均为50 m;观测点高程为地面上25 m,测点间距为50 m,共有20×20=400个采集数据。
反演数据为添加3%的高斯白噪声的正演模拟结果。在Marquardt反演和Occam反演中,=4,=1,=1,=1,=0.0005,=1.8,如图2(b)~(c)[24−26]所示;在图2(d)中,聚焦算子为=diag[(2+2)−1/2],=1.2×10−6。
在图2(b)和(c)中两者效果相当,两者在深度上的分辨率均较低,异常底板分界面非常模糊,难以辨识;而聚焦反演取得了较清晰的边界,由于聚焦作用的影响,存在过度聚焦的现象(见图2(d)),即反演得出异常的规模远比实际的要小,而异常幅值要比实际正演模型的大得多。
图3所示为种植反演结果及其密度模型切片。此处需要注意的是:在反演结果中,所有已赋值的网格单元的密度均为0.30 g/cm3。在图3(a)中,出现部分浅色且低密度网格,表明切片未能切割到该网格,而其密度值仅为切片两侧网格密度值和的平均值,即 0.15 g/cm3。
由于在种植反演所有网格仅涉及到至多一次正演计算,因而其反演速度较快、及内存消耗较小。相比于图2中多种反演方法相比,本研究中种植反演的重构轮廓与正演模型的相当,且更为规整,这表明了本研究中算法的可靠性。

图2 正演模型Ⅰ及其不同方法的反演效果对比
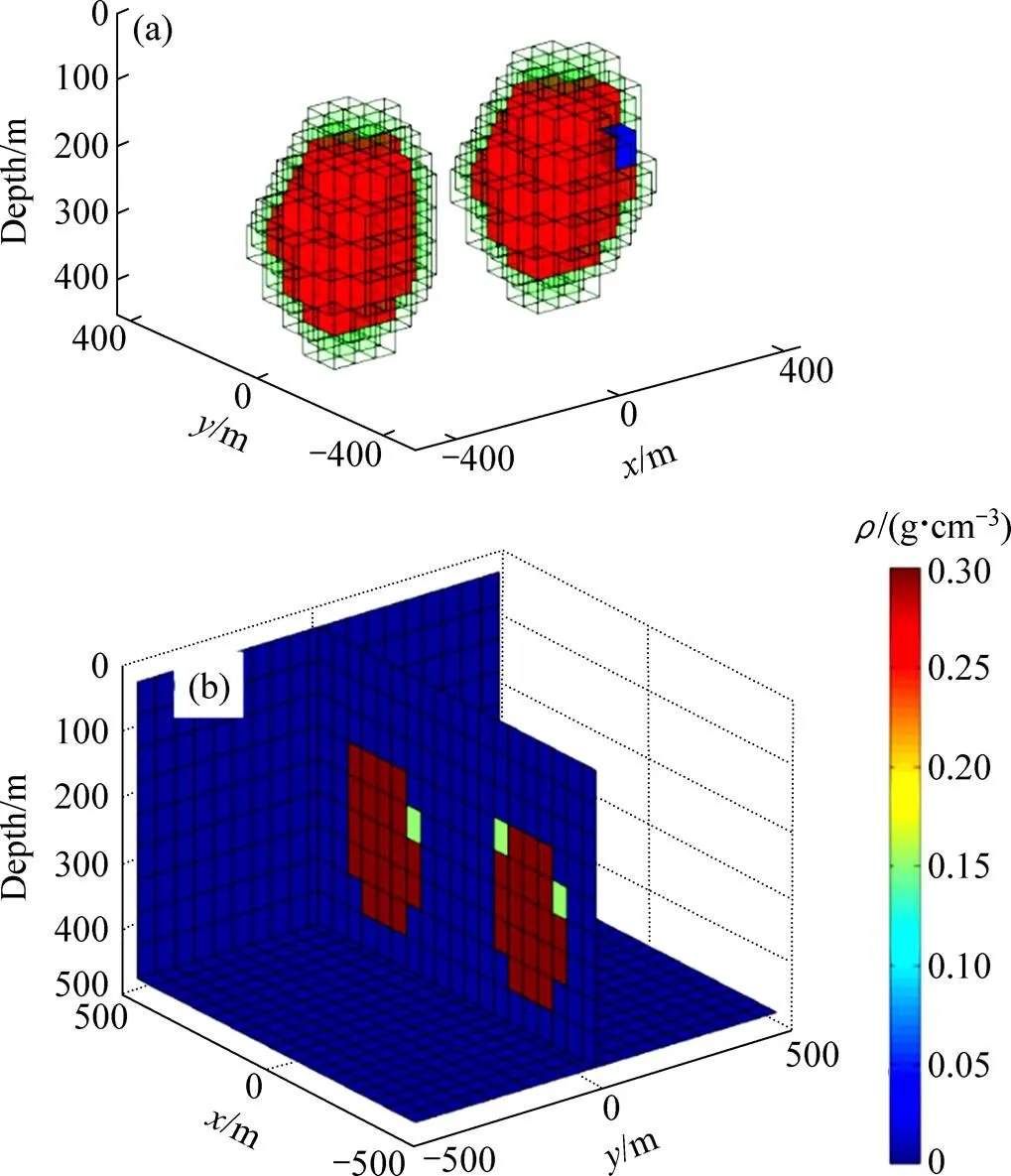
图3 重力梯度张量种植反演结果
3 计算性能分析
对于传统点元法而言,反演核系数矩阵所需存储核函数的个数N,为观测点数N与物性网格个数N的乘积;对于种植反演而言,反演核系数矩阵所需存储核函数的个数是变化的。随着迭代次数iter和种子个数seeds增大,种植反演搜索空间呈现出急剧增大的趋势,即邻域网格的个数。如图 2所示,对于单一种子的种植反演而言,迭代一次将增加了5个派生网格。在不考虑某些最优网格与其它最优网格存在相同邻域网格的情况下,第iter次迭代时,由等差数列关系可以计算所需存储核函数的个数:
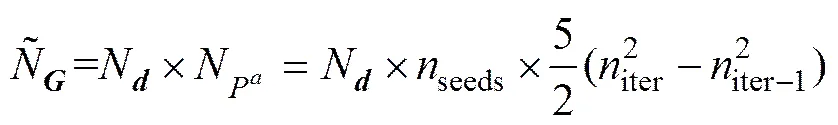
(6)
因而随着种子个数的增加,能有效的降低种植反演的迭代次数;进而,可进一步降低核系数矩阵所需存储核函数的个数。
图4所示为不同方法的反演参与计算的网格数的对比图,曲线1为种植反演的迭代次数与涉及反演计算网格数的关系曲线,曲线2为类似Marquardt 反演、Occam反演和聚焦反演等传统反演方法的迭代次数与涉及反演计算网格数的关系曲线,曲线3为基于式(6)预测给出的迭代次数与涉及反演计算网格数的关系曲线。从图4可以看出,随着迭代次数的增加,曲线3能大体预测出涉及种植反演的计算网格数但其仍然远比实际涉及种植反演实际涉及的计算网格数要大;然而对比种植反演(曲线1和曲线3)和传统反演方法(曲线2),可以发现传统反演方法所涉及计算网格数不随迭代次数的变化,且一直在比较高的水平。因而重力及重力梯度张量种植反演所需计算机内存小。
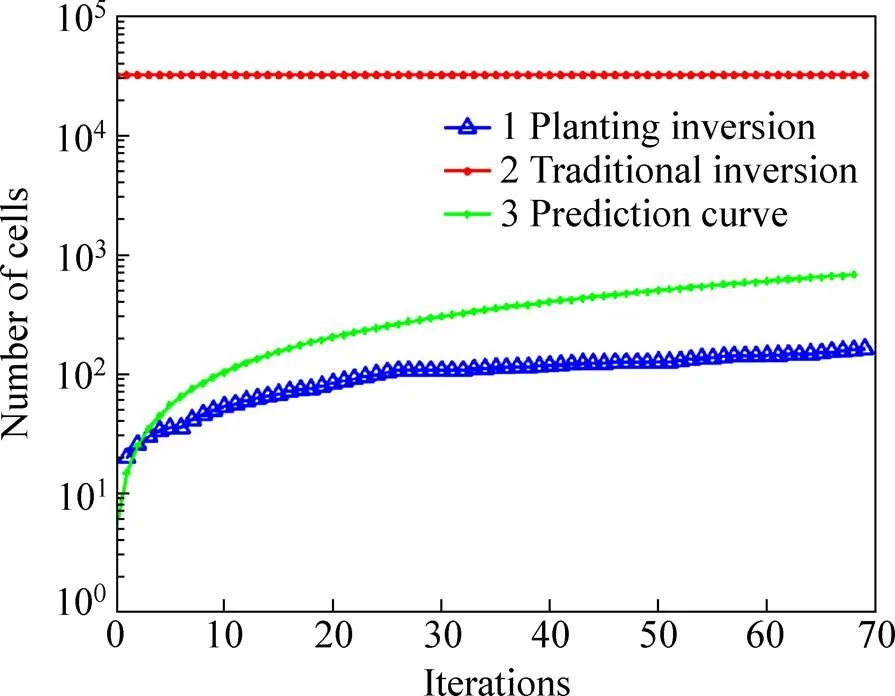
图4 对比不同方法的反演参与计算的网格数
4 种子密度值对种植反演的影响
针对二进制反演中,所设定密度值对反演结果密度分布有非常大的影响。在图1示例的基础上,不改变原有种子的空间位置,而改变其(1,2)密度值,通过设置多组模型,研究种子密度值对种植反演结果的影响。
如图5所示,共测试了6组模型。由种植反演方法的计算量或反演迭代次数与反演中所赋予密度的网格数目以及这些网格的邻域网格成正比。可以发现种子的密度值能极大的影响种植反演方法重构的结果。如图5(a)~(d)所示,当种子的密度值过低时,易于导致相邻异常的侵入,导致最终重构模型与实际情况差别很大;当种子的密度值与实际情况较为一致时(见图5(e)),种植反演方法重构模型与实际情况较为一致;当种子的密度值小于实际情况时(见图5(c)和(d)),易于导致反演重构密度分布范围远大于实际情况,这将极大的增加反演迭代次数,降低反演效率;与之相对的是,当种子的密度值远大于实际情况时(见图5(a)和(f)),将使得重构模型极度聚焦。
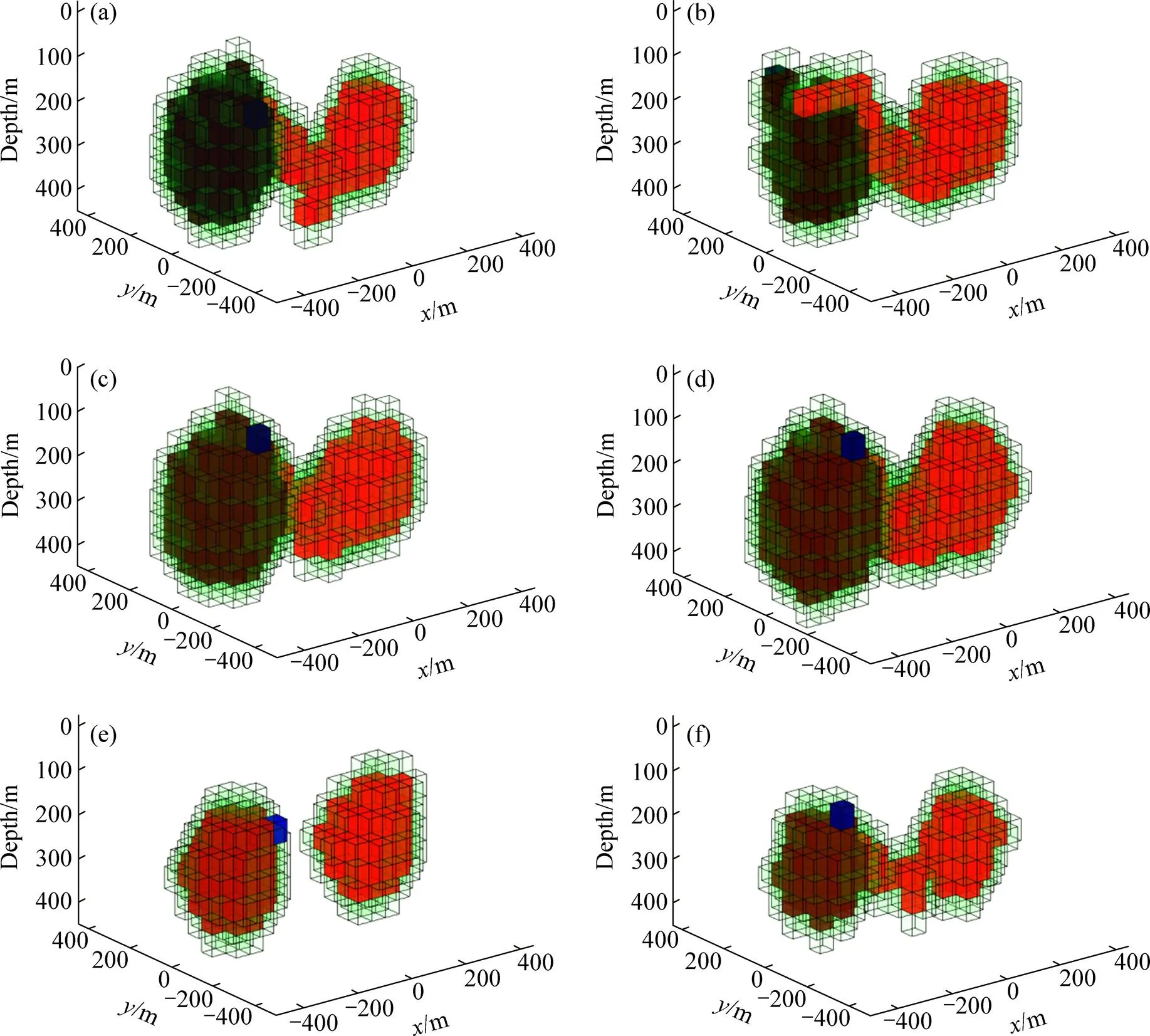
图5 不同密度值的种子种植反演结果
5 基于位场水平衰减特性加权函数
在种植反演中,密度吸引子的位置决定了重构密度模型的空间分布,随着重构模型增大,邻域网格的数量也在逐步增大,密度吸引子到邻域网格间的间距也在增大,使得某一个方向邻域网格始终被确定为最优网格,最终导致相邻异常源间出现相互侵入的现象。为此,引入一个基于位场水平衰减特性加权函数w限制密度吸引子的作用范围,以期使密度吸引子忽略较远的异常源,减弱相邻异常源相互侵入的趋势:

式中:s和s为密度吸引子的水平位置,和为观测点水平位置,L为密度吸引子的作用范围,为水平衰减因子,对于重力梯度张量数据的反演,一般在4~6之间。需要注意的是,w仅作用于种植反演的差残估计部分的计算,而不直接作用于目标函数。当差残估计过大时,最优网格将始终不被赋于密度值,从而使得密度吸引子仅在一定的区域内起作用。
首先,以一孤立异常源为例,分别对比水平加权和非加权状态下的效果。
图6所示分别为孤立异常源不带水平加权函数和带水平加权函数种植反演g数据的结果,在图6(b)中=450平面上二维图形为水平加权函数的权重分布图,由w定义可知,w为0~1分布的衰减函数。通过以上结果的对比分析,可以发现带水平加权函数的种植反演在水平方向上更为规整,而不带水平的反演结果在各方向上均较为散乱。

图6 gzz分量种植反演结果
对于多异常源而言,水平加权函数的作用最为关键的是:权函数的加载方式和最优网格的判断方式及多分量联合反演的方式,对于前者主要有如下两种方式:其一、分别加载各单一密度吸引子的水平加权函数w,其二、将各密度吸引子的水平加权函数w进行叠加;对于后者主要对应如下两种方式:其一、以式(1)或式(4)单独计算各密度吸引子的数据泛函和目标函数P(),其二、以式(1)或式(4)计算数据泛函和目标函数P();对于多分量反演而言,基于式(1)的种植反演于分量的组合形式无关,而基于式(4)的种植反演,则差别相对较大,主要是由于缩放因子的计算方式于分量组合形式相关。
以埋深相同密度不同的组合模型为例,分析、研究水平加权函数的有效加载方式。特构建如下所示模型:在地下空间存在埋深为250 m的两个大小均为200 m×200 m×200 m异常体,剩余密度分别为0.1 g/cm3(绿色线框)和0.3 g/cm3(蓝色线框),观测点高程为地面上25 m,观测点间距为50 m,共有40×40=1600个观测点。并将含3%的高斯噪声的正演结果中作为反演数据。
图7所示分别为各密度吸引子水平加权函数叠加及单独作用的g分量种植反演结果。由于在同一次种植反演迭代中,遍历不同密度吸引子的邻域网格和更新其最优网格后的重构密度模型的差异极小,仅有一个新的最优网格产生,故只显示迭代终止时的重构密度模型及与最后一个密度吸引子相对应的水平加权函数。通过以上种植反演结果的对比,两种权函数加载模式的反演效果相似。
图8所示分别为不同水平加权函数加载方式及不同多分量处理方式的种植反演结果。由于各重力梯度张量分量核函数幅值差异极大,故在图8(c)和(d)中各分量在合并为单一分量之前已经进行了归一化。通过以上反演结果的对比分析,可以看出图8(a)在重构密度差异上部最不规整,导致上述问题的主要原因是相邻异常源相互干扰;而图8(b)和(d)在深度方向则远超出真实模型,导致上述问题的主要原因是采用式(4)计算多个分量并将各个结果求和,将最终放大数据泛函,但随着深度的增加,物性网格的响应变小,此时深部的物性网格的数据泛函变小,因而最优网格将逐步沿深度方向增加,并最终造成重构密度模型在深度方向上远远超出真实模型的范围。

图7 gzz分量种植反演结果

图8 种植反演结果
6 结论
1) 在种植反演中,当密度吸引子的密度值过低时,易于导致相邻的异常侵入,导致最终重构模型发生畸变,且与实际情况差别很大;当密度吸引子的密度值小于实际情况时,易于导致重构密度分布范围远大于实际情况,这将极大的增加反演迭代次数和降低反演效率;当密度吸引子的密度值远大于实际情况时,将使得重构模型过度聚焦。
2) 当密度吸引子相对较浅时,易于导致“趋肤”效应的产生;而当密度吸引子相对较深时,重构密度模型整体下移。
3) 对于基于位场水平衰减特性加权函数的加载方式,水平加权函数单独加载的全张量联合反演的效果最优。
4) 当密度吸引子水平位置偏离异常源中心时,种植反演通过最优网格选取策略,修正因密度吸引子空间位置偏离异常源的问题,使得新近赋值的网格单元逐步接近于实际异常体中心,但无法改变其前期已经错误赋值的情况,而这些错误赋值的网格单元将最终导致重构密度模型出现一定地畸变。故此,在本文中,不就密度吸引子水平位置偏离异常源中心的情况进行讨论,将另撰文详述并引入其他方法处理该问题。
REFERENCES
[1] 陈召曦, 孟小红, 郭良辉, 刘国峰. 基于GPU并行的重力, 重力梯度三维正演快速计算及反演策略[J]. 地球物理学报, 2012,55(12): 4069−4077. CHEN Zhao-yi, MENG Xiao-hong, GUO Liang-hui, LIU Guo-feng. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU[J]. Chinese Journal of Geophysics, 2012, 55(12): 4069−4077.
[2] 吴文鹂, 高艳芳, 顾观文. 起伏地形重磁三维快速正演计算[J]. 物探化探计算技术, 2009,31(3): 179−182. WU Wen-peng, GAO Yang-fang, GU Guan-wen. Gravity and magnetic 3-D fast forward computing with varying Topography[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2009, 31(3): 179−182.
[3] 姚长利, 郝天珧, 管志宁, 张聿文. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003,46(2): 2252−2258. YAO Chang-li, HAO Tian-yao, GUAN Zhi-ning, ZHANG Yu-wen. High speed computation and efficient storage in 3D gravity and magnetic inversion based on genetic algorithms[J]. Chinese Journal of Geophysics, 2003, 46(52): 2252−2258.
[4] 曹书锦, 朱自强, 鲁光银, 曾思红, 郭文斌. 基于单元细分 H-自适应有限元全张量重力梯度正演[J]. 地球物理学进展, 2010,25(3): 1015−1023. CAO Shu-jin, ZHU Zi-qiang, LU Guang-yin, ZENG Si-hong, GUO Wen-bin. Forward modelling of full gravity gradient tensors based H-Adaptive mesh refinement[J]. Progress in Geophysics, 2010, 25(3): 1015−1023.
[5] WANG Jun, MENG Xiao-hong, LI Fang. A computationally efficient scheme for the inversion of large scale potential field data: Application to synthetic and real data[J]. Computers & Geosciences, 2015, 85 (Part A): 102−111.
[6] TALWANI M. Nonlinear inversion of gravity gradients and the GGI gradiometer[J]. Central European Journal of Geosciences, 2011, 3(4): 424−434.
[7] WU L, CHEN L. Fourier forward modeling of vector and tensor gravity fields due to prismatic bodies with variable density contrast[J]. Geophysics, 2016, 81(1): G13−G26.
[8] CHEN Zhao-xi, MENG Xiao-hong, GUO Liang-hui, LIU Guo-feng. GICUDA: A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA[J]. Computers & Geosciences, 2012, 46: 119−128.
[9] UMA MARTIN, ZHDANOV M S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs[J]. Computers & Geosciences, 2014, 62: 80−87.
[10] WILSON G, ČUMA M, ZHDANOV M S. Massively parallel 3D inversion of gravity and gravity gradiometry data[J]. Preview, 2011, 2011(152): 29−34.
[11] LI Y, OLDENBURG D W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method[J]. Geophysical Journal International, 2003,152(2): 251−265.
[12] 吴小平, 徐果明. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 2000,43(3): 420−427. WU Xiao-ping, XU Guo-ming. Study on 3D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420−427.
[13] 刘银萍, 王祝文, 杜晓娟, 刘菁华, 许家姝. 基于Extrapolation Tikhonov正则化算法的重力数据三维约束反演[J]. 地球物理学报, 2013,56(5): 1650−1659. LIU Yin-ping, WANG Zhu-wen, DU Xiao-juan,LIU Jing-hua, XU Jia-shu. 3D constrained inversion of gravity data based on Extrapolation Tikhonov regularization algorithm[J]. Chinese Journal of Geophysics, 2013, 56(5): 1650−1659.
[14] COMMER M, NEWMAN G A. New advances in three-dimensional controlled-source electromagnetic inversion[J]. Geophysical Journal International, 2008,172(2): 513−535.
[15] CARDARELLI E, FISCHANGER F. 2D data modelling by electrical resistivity tomography for complex subsurface geology[J]. Geophysical Prospecting, 2006,54(2): 121−133.
[16] ZHDANOV M S, LIU X, WILSON G A, WAN L. 3D migration for rapid imaging of total-magnetic-intensity data[J]. Geophysics, 2012,77(2): J1−J5.
[17] ZHDANOV M S, LIU X, WILSON G A, WAN L. Potential field migration for rapid imaging of gravity gradiometry data[J]. Geophysical Prospecting, 2011,59: 1052−1071.
[18] COX L H, WILSON G A, ZHDANOV M S. 3D inversion of airborne electromagnetic data using a moving footprint[J]. Exploration Geophysics, 2010,41(4): 250−259.
[19] LORIS I, NOLET G, DAUBECHIES I, Dahlen F. Tomographic inversion using L1-norm regularization of wavelet coefficients[J]. Geophysical Journal International, 2007,170(1): 359−370.
[20] CLAERBOUT J F, MUIR F. Robust modeling with erratic data[J]. Geophysics, 1973,38(5): 826−844.
[21] LAST B, KUBIK K. Compact gravity inversion[J]. Geophysics, 1983,48(6): 713−721.
[22] STOCCO S, GODIO A, SAMBUELLI L. Modelling and compact inversion of magnetic data: A matlab code[J]. Computers and Geosciences, 2009,35(10): 2111−2118.
[23] UIEDA L, BARBOSA V C. Robust 3D gravity gradient inversion by planting anomalous densities[J]. Geophysics, 2012,77(4): G55−G66.
[24] THANASSOULAS C, TSELENTIS G A, DIMITRIADIS K. Gravity inversion of a fault by marquardt’s method[J]. Computers & Geosciences, 1987, 13(4): 399−404.
[25] CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289−300.
[26] ZHDANOV M S, ELLIS R, MUKHERJEE S. Three- dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004, 69(4): 925−937.
(编辑 何学锋)
Planting inversion of tensor gravity data
CAO Shu-jin1, 2, 3, ZHU Zi-qiang2, LU Guang-yin2
(1. Hunan Provincial Key Laboratory of Shale Gas Resource Utilization,Hunan University of Science and Technology, Xiangtan 411201, China;2. School of Geosciences and Info-physics, Central South University, Changsha 410083, China;3. School of Resource Environment and Safety Engineering,Hunan University of Science and Technology, Xiangtan 411201, China)
Large-scale inversion of gravity gradient tensor data is a time-consuming problem with high demands on computational and physical memory usage. To avoid extraordinary matrix-vector multiplications in each inverse iteration and to speed up the forward of geophysical models, planting inversion is introduced and conjugate gradient iteration replaced by accumulation summary based on L1 norm. The planting inversion easily leads to adjacent anomalies mutually invasive, a horizontal weighted function is proposed to suppress mutual interference between the adjacent anomaly sources. These results of the inversions and analysis results show that planting inversion with horizontal weighted function obtain a meaningful geophysical model. And these methods require little memory and high efficiency.
planting inversion; horizontal weighted function; gravity gradient tensor; L1 norm
Project(E51651) supported by the Doctoral Foundation of Hunan University of Science and Technology; Project(16K031) supported by the Scientific Research Fund of Hunan Provincial Education Department of China; Project(2017JJ3069) supported by Natural Science Foundation of Hunan Province of China; Projects(41174061, 41374120) supported by the National Natural Science Foundation of China
2014-07-13; Accepted date:2017-03-31
ZHU Zi-qiang; Tel: +86-13507319431; E-mail: 13507319431@csu.edu.cn
10.19476/j.ysxb.1004.0609.2017.05.017
1004-0609(2017)-05-0997-09
P631.1
A
湖南科技大学博士科研启动基金资助项目(E51651);湖南省教育厅科研项目(16K031);湖南省自然科学基金资助项目(2017JJ3069);国家自然科学基金资助项目(41174061,41374120)
2014-07-13;
2017-03-31
朱自强,教授,博士;电话:13507319431;E-mail:13507319431@139.com

