Al6061板料的修正GTN损伤模型

韩晓兰，赵升吨，徐 凡，陈 超，赵仁峰



Al6061板料的修正GTN损伤模型

韩晓兰1，赵升吨1，徐 凡1，陈 超1，赵仁峰2

(1. 西安交通大学机械工程学院模具与先进成形技术研究所，西安 710049；2. 西安理工大学机械与精密仪器工程学院，西安710048)

为了获得GTN-Hill1948细观损伤模型中的参数，设计带凹槽的试样和剪切试样并进行拉伸试验，获得两种Al6061板料试样的载荷−位移曲线。基于ABAQUS 软件建立Al6061板料的有限元模型，应用反向优化法标定GTN-Hill1948细观损伤模型中的初始孔洞体积分数和剪切损伤参数，并设计带孔的拉伸试样对损伤模型进行实验验证。结果表明：通过反向优化法来标定的GTN-Hill1948模型中的初始孔洞体积分数为0.0005、剪切损伤参数为2；中间带孔的试样验证所标定参数的正确性，该损伤模型可以有效地预测Al6061板料发生断裂的位置。

Al6061板料；GTN-Hill1948损伤模型；损伤演化；反向优化法

近年来，随着汽车节能减排的要求，无铆连接已经成为汽车轻量化的关键技术之一[1]。铝合金由于具有密度低、强度较高、塑性好等优点已经被广泛应用于无铆连接中[2]。但是在实现无铆连接时板材常产生接头质量不稳定或断裂失效等问题，其断裂方式是由损伤累积产生的韧性断裂[3−4]。其韧性断裂过程经历5个阶段：即微孔洞的形核、长大、聚合直至产生塑性变形局部化，最终产生宏观裂纹。为了深入研究无铆塑性连接的失效演化机理，建立合理的本构模型是首要的任务。

材料的韧性断裂属于细观损伤力学的范畴[5]，QUAN等[6]采用Cockcroft-Latham损伤准则有效地预测量材料加热过程中发生断裂的位置及时刻。ZHANG等[7]通过Cockcroft-Latham损伤模型预测了镁合金板材轧制边发生断裂的条件，但是该模型忽略了空穴之间的交互作用。目前发展较为完善应用较为广泛的细观损伤模型GTN损伤模型是由GURSON[8]在1975提出，并由TVERGAARD等[9]相继完善的GTN (Gurson-Tvergaard-Needleman)模型。由于GTN模型存在不同的修正形式且模型参数为内变量，难以完全依靠实验获得全部模型参数。目前常用的获得该模型参数的方法是结合材料实验和有限元分析的反向优化法[10]。王明正等[11]通过反向优化法获得了GTN损伤模型的参数，该模型可以有效预测钛合金塑性成形的过程。石柏军等[12]利用45号钢的GTN损伤模型有效地预测了无铆连接过程中接头最容易发生断裂的位置。ZHAO等[13]用GTN损伤模型和实验相结合的方法有效地预测了Al5052 和Q235板材发生失效的位置。但是，目前关于Al6061的损伤模型报道较少[13−15]。

本文作者主要针对无铆连接用板材Al6061，设计了带凹槽的试样和剪切试样，通过采用反向优化法获得GTN-Hill1948细观本构模型的损伤参数，并设计中间带孔的试样对细观损伤参数进行验证。

1 GTN损伤模型简介

本研究采用的GTN模型为NAHSHON等[16]在2009年基于NAHSHON等[17]提出的模型进一步拓展和修正的模型，如式(1)所示：

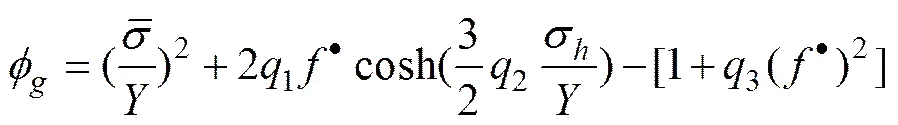
式中：1、2、3是代表了材料的本质属性与材料的微孔有直接的关系，1和3的关系可以写成。代表了等效应力，代表塑性流动应力。损伤变量是总的等效孔洞体积分数，它是孔洞体积分数的函数，由TVERGAARD等[9]引入以解释由于孔洞聚合导致材料承载能力逐渐下降的现象。当=0时，表明材料没有损伤，上述屈服方程退化为标准的Mises屈服方程。无损伤时的屈服强度为，静水压力表示为，而且等效应力为，在这里为应力偏张量。

在NAHSHON等[16]修正的GTN损伤模型的参数中，包含了1、2和3；初始的孔洞体积分数0；孔洞聚合参数N；平均形核应变率N；标准差N；临界孔洞体积分数c；最终的失效孔洞体积分数f；剪切损伤参数k。TVERGAARD等[9]建议将损伤参数1、2和3定义成1=1.5、2=1和3=2.25。GULLERUD等[18]提出了一个经验值c的取值范围为(0.1~0.2)，而失效时孔洞断裂体积分数f被设置成0.25，N被定义成0.04，N被定义成0.3，N被定义成0.1[18−22]。根据文献[23−24]的研究，将Al6061的临界孔洞参数c设置成0.15。因此，在GTN损伤模型中需要进行标定的参数主要包括初始孔洞体积分数0和剪切损伤参数k。

由于建立GTN-Hill1948损伤模型的假设条件是材料内部有微孔，在塑性变形过程中逐渐长大，并且伴随新微孔的形核，最后失稳时产生聚合。因此，在确定GTN损伤参数时首先应当建立合适的有限元模型[11, 25−26]，然后通过有限元分析和实验相结合的反向优化方法获得损伤模型参数。

2 实验

2.1 试样制备

试验所用材料为铝合金Al6061，板材厚度为2 mm。拉伸试样按照金属拉伸试验方法(GB228—87)、金属拉伸试验试样(GB6397—86)等国标进行加工。图1(a)所示中的带凹槽试样是为了获得修正的GTN损伤模型中的初始孔洞体积分数0，图1(b)中所示的剪切试样是为了标定剪切损伤参数。通过对两种拉伸试样进行准静态拉伸实验，标定板料的损伤参数。图1(c)所示为带孔试样，该试样是为了验证所标定的损伤参数的正确性和合理性，确保模型的承载能力。

2.2 试验方法

材料的拉伸实验在西安交通大学材料学院力学中心进行，设备为INSTRON试验机，对2 mm的Al6061板料进行拉伸试验。图2(a)所示为测试初始孔洞体积分数0的样本，单向拉伸带凹槽试样件装卡方式如图所示，在试验中为精确测量位移信号，采用标距为25 mm的引伸计。为达到准静态加载的目的，拉伸速度选为2 mm/min。在这个过程中由于断裂通常发生在凹槽的中间位置，因此在装夹引伸计时需要避开断口发生的位置。图2(b)所示为测试剪切损伤参数的样本，该样本在断裂时，会出现偏载，而且样件设计尺寸较大，因此，进行剪切试验时需借助夹具实现，剪切试样通过自制夹具及销钉固定在试验机上，详细装夹方式可参考图2(b)；为了精确测量位移信号，试验时在试样表面粘贴上相距10 mm的两片刀片，并装卡标距为10 mm的引伸计(COD式)；加载速度选为2 mm/min，试验中随着位移的增加，刀口逐渐移动，引伸计逐渐张开并将信号输送至计算机采集系统。图2(c)所示为验证损伤样本的装夹方式，其断裂发生在剪切带交叉的位置，其装夹方式同图2(a)相近。以上试验中均以试样完全断裂时结束试验，并记录位移−载荷曲线。

图1 试样的形状和尺寸

图2 标定损伤参数的实验

3 结果与讨论

基于ABAQUS 软件，对板材的3种试样进行有限元分析。由于图1(a)、(b)和(c)试样中均存在变形集中区域，所以为了能够准确地描述试样的变形，采用C3D8R三维实体单元建模。为了能够节约有限元时间又不丧失有限元精度，在变形集中区域使用了细网格，材料模型使用修正的GTN-Hill1948损伤本构模型来描述其力学行为；而在远离变形集中区域则使用了粗网格，并在粗细网格交界区域使用过渡网格划分。

3.1 初始孔洞体积分数0的标定

通常标定初始孔洞体积分数0时需要做金相分析，测量抛光后夹杂等在材料中所占体积分数，但是抛光后的铝合金中包含部分夹杂和微孔洞，严格进行定量分析初始孔洞体积分数0仍然存在困难。目前常采用反向优化法来标定初始孔洞体积分数0。其核心思想是设初始孔洞体积分数0为优化变量，通过有限元分析获得载荷−位移曲线，并与试验结果的载荷−位移曲线相对比，取得误差最小的常数作为优化的最终解。在确定初始孔洞体积分数0时，首先根据经验数据设定初始孔洞体积分数0的取值范围，通过对比取值范围内不同初始孔洞体积分数0和试验获得载荷−位移曲线来获得初始孔洞体积分数0。

HE等[27]通过扫描电镜获得铝合金5052的初始孔洞体积分数0为0.0029，GUO等[28]通过反向优化法获得5052BD-H14的初始孔洞体积分数0为0.0001。ZHAO等[13]通过反向标定法获得铝合金5052-O的初始孔洞体积分数0为0.0005和Q235的初始孔洞体积分数0为0.0001，铝合金4004的初始孔洞体积分数0为0.005[29]。不同的材料或者相同的材料不同的状态初始孔洞体积分数0也会有差异。因此，本研究基于上述文献的成果，选取0的初始取值分别为0.0001、0.0002、0.0003、0.0005和0.001。为了确定初始孔洞体积分数，首先通过对如图1(a)所示的凹槽试样进行拉伸试验，获得试验所需的载荷−位移曲线，其失效样本如图3(a)所示。在拉伸力的作用下，应力集中作用在断口的凹槽附近，即变形主要集中发生在最小断面处，属于拉断模式。其次建立Al6061的带凹槽的单向拉伸试样的3D有限元模型(见图3(b))，在拉伸实验中，拉伸速度为2 mm/min，忽略板料的弹性变形，再次对拉伸试验和有限元分析获得的载荷−位移曲线进行对比分析(见图4)。

图3 带凹槽试样的有限元模型

从图4可以看出，初始孔洞体积分数0明显影响载荷−位移曲线的变化趋势。当初始孔洞体积分数0增加时，断裂韧性降低而且比较容易发生断裂。当初始孔洞体积分数0为0.0001时，载荷−位移曲线偏离实验值。因此，可以断定初始孔洞体积分数0为0.0001时，该GTN-Hill1948损伤模型不能很好预测在拉力作用下的失效行为。当初始孔洞体积分数0为0.0005时，载荷−位移曲线接近实验值，该初值能够很好地预测板料的失效行为，因此，将初始孔洞体积分数0设置为0.0005，作为Al6061板料的初始孔洞体积分数。通过对载荷−位移曲线的比较可以说明初始孔洞体积数0影响样件的承载能力和失效行为，且将它作为修正的GTN-Hill1948损伤模型中的初值。

图5所示为采用修正的GTN-Hill1948损伤模型获得的损伤演化图(初始孔洞体积分数0为0.0005和临界孔洞体积分数c为0.15)，包括损伤参数和应力分布。从图5可以看出，板料首先发生损伤的位置为中心区域，在中心区域应力集中，中心区域开裂后断裂迅速向边缘扩展，造成断面形貌基本与加载方向垂直的面，属于严重受拉后开裂，与试验结果基本一致。断裂基本上经历了剪切带局域化，剪切带扩展，缺陷产生，扩展直至断裂。图中可以明显看出，应力集中区也是损伤集中区，应力最集中点即为开裂点，而且先产生剪切带的区域是发生断裂的区域。

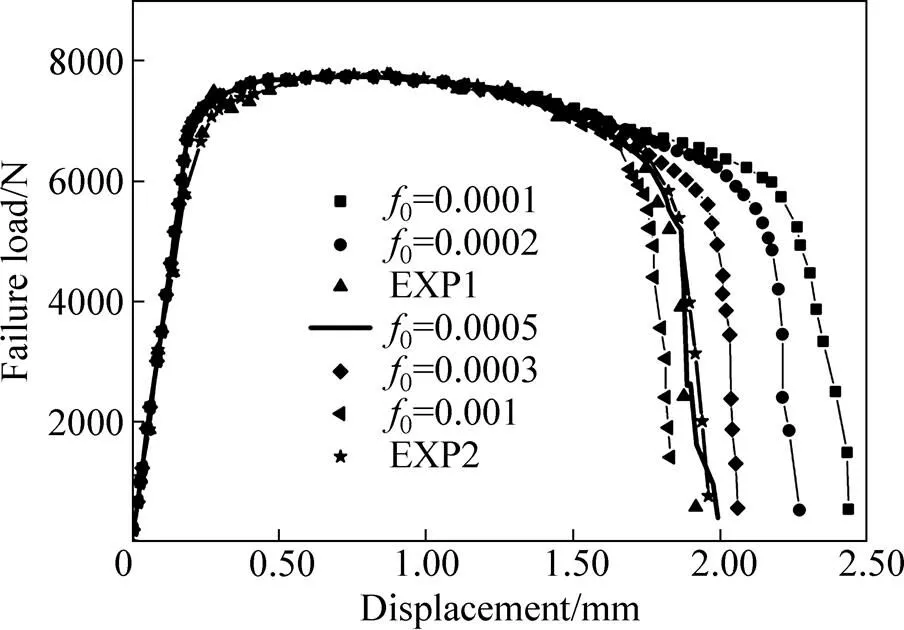
图4 拉伸试验和有限元分析的载荷−位移曲线

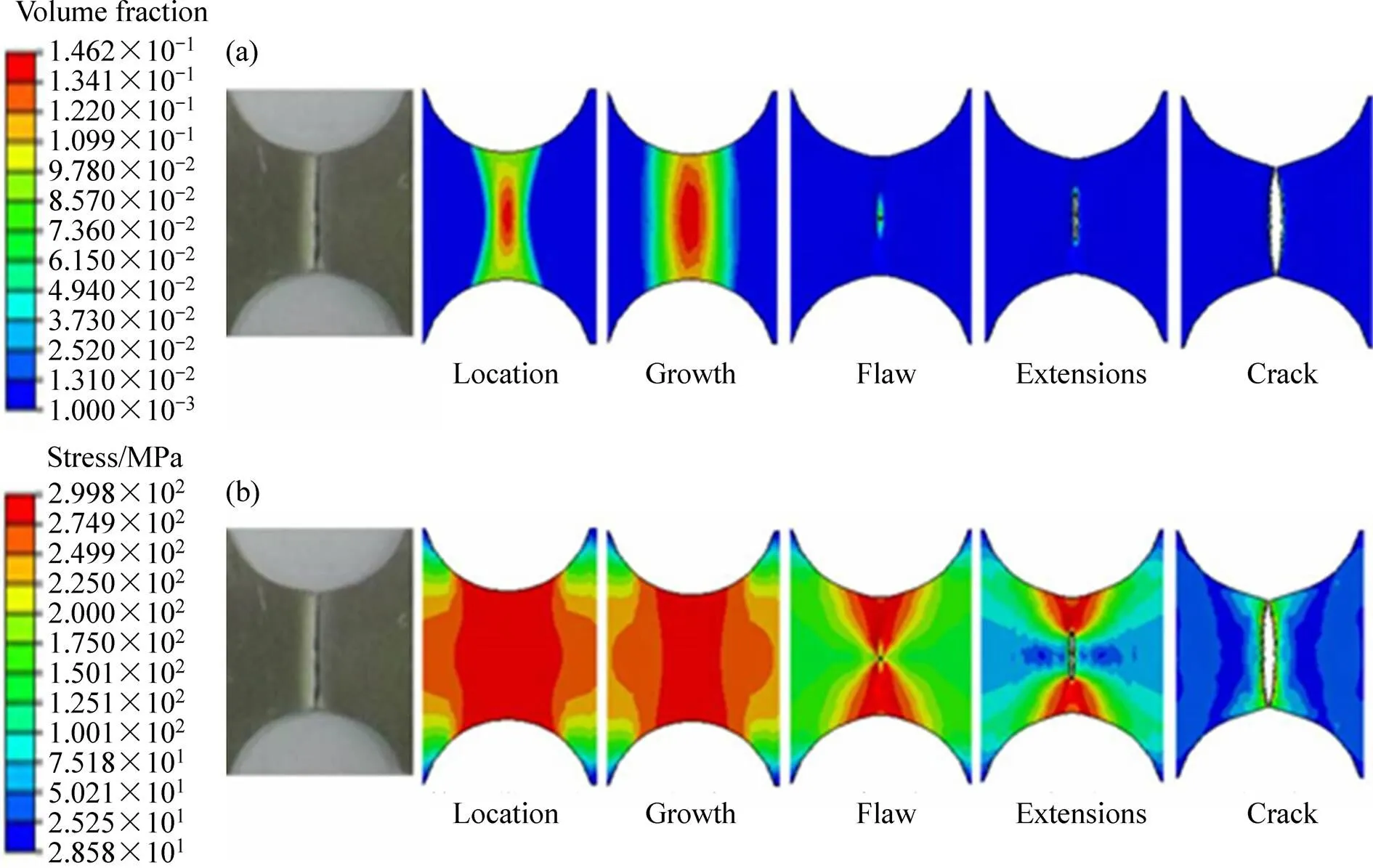
图5 在f0=0.0005和fc=0.15时拉伸试样的损伤演化过程

3.2 剪切损伤参数k

当初始孔洞体积分数0确定时，剪切损伤参数k可以由剪切试验来标定。已知k为正数，但是并不能够事先预测出k的范围。当假设初始孔洞体积分数0为0.0005，采用反向优化法来标定剪切损伤参数k。为了确定剪切损伤参数k，设置了5个试验常数k=0、0.5、1、1.5和2。图6(a)所示为剪切损伤试样和有限元模型，图6(b)所示为剪切损伤测试的载荷−位移曲线。图7所示为剪切损伤参数k=2.0和初始孔洞体积分数0=0.0005时，剪切试样的失效演化过程，包括损伤参数和应力分布情况。通过比较实验和有限元曲线可以确定剪切损伤参数k影响GTN-Hill1948细观损伤模型的预测能力，当剪切损伤参数k增加时，断裂韧性下降。由图6(b)可知，当剪切损伤参数k为0时，断裂韧性最好。损伤模型退化成原始的GTN损伤模型，也就意味着载荷−位移曲线偏离Al6061的剪切实验值。经过对比可知，k的取值范围在1.5~2.0之间。从图6(b)还可以看出，当k为0时，有限元获得的结果严重偏离试验结果，也反映出原始模型在预测剪切损伤时的不足，因此必须对模型进行修正才能更好的预测材料的剪切损伤过程。要想精确计算k，则需在上述粗略推算其取值范围的基础上，再经过多次计算才能最终确定其精确值。最后，确定该材料的剪切影响因子k为2.0。随着位移的增加，出现局部剪切带，剪切带聚合，失效产生，扩展直到断裂。从图7可以看出，在材料的弹性及塑性阶段初期，该模型给出的有限元结果与试验结果比较接近，说明优化的硬化关系能够较好地描述材料的硬化行为，而且在载荷发生下降段的部分有限元结果与试验结果较为接近，说明采用修正的GTN-Hill1948细观损伤模型能够较好地描述材料在剪切时的失效演化过程，同时也说明由该试验及有限元所确定的剪切影响因子k的值基本 正确。

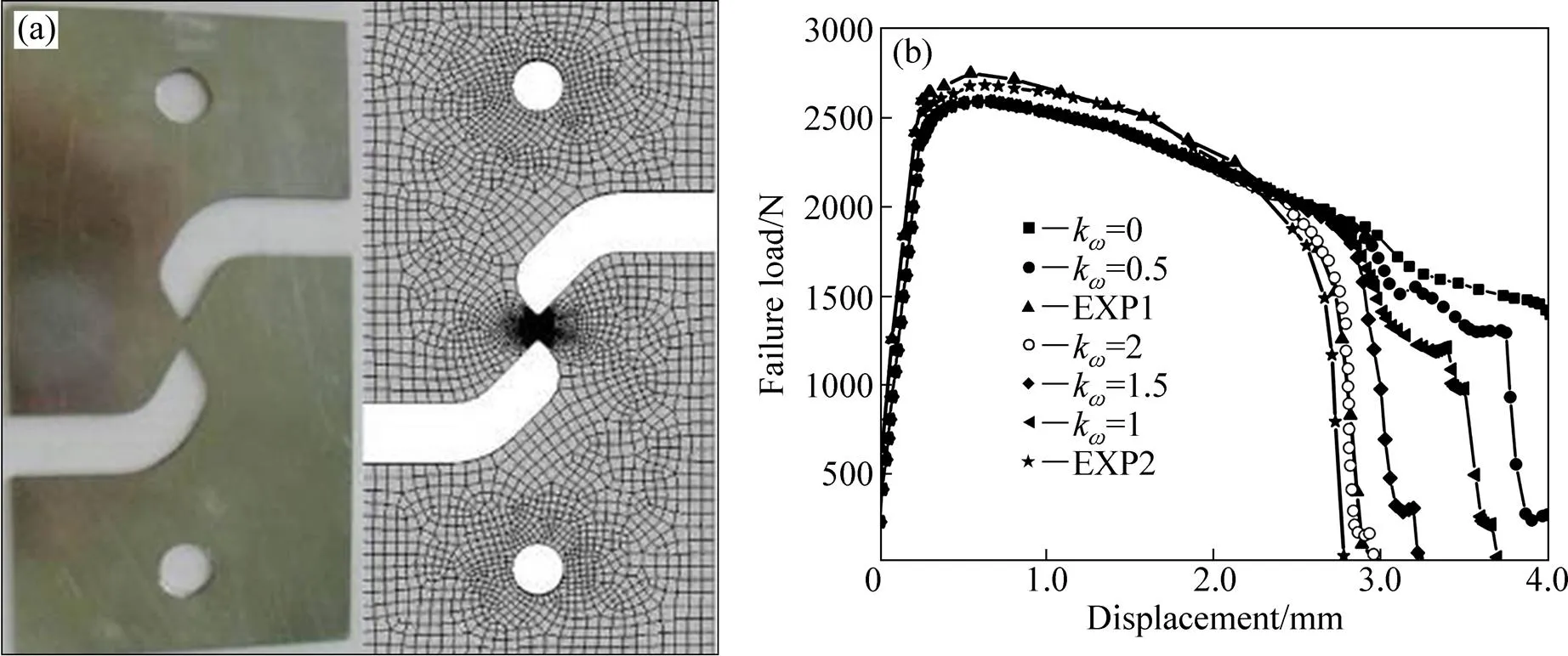
图6 剪切损伤参数的标定kω=0, 0.5, 1, 1.5, 2

图7 在f0=0.0005和kω=2时剪切试样的损伤演化过程

3.3 损伤参数的验证

当修正的GTN-Hill1948损伤模型中的参数确定后，需要对模型的预测能力进行验证。在此，通过设计带孔洞验证试样(见图1(c))对损伤模型进行实验验证。图8所示为带孔洞验证试样的载荷−位移曲线，模拟中心带孔样件的承载能力。有限元分析的位移−载荷曲线和实验结果基本一致，因此修正的GTN-Hill1948细观损伤模型能够准确地预测材料的失效演化过程。研究认为材料一旦形成I型裂纹，材料的断裂模式即转变为剪切断裂，形成剪切断口。

图9所示即为中间带孔板料的断口宏观形貌和有限元失效过程(损伤参数和应力的分布情况)。板料在拉伸过程中，圆孔处于应力集中状态，断裂首先发生在圆孔处形成I型裂纹，最终扩展至边缘导致断裂。损伤过程可以分成5个阶段，即剪切带形成、长大、起裂、裂纹扩展和完全断裂。在剪切带交叉的部位开始断裂，促进了某一方向剪切带的发展。从演化图中可以看出，损伤最先发生在材料中间并形成X型剪切带，由于具有较高的应力三轴度而导致损伤在此发生。剪切带上孔洞汇合并导致试样最终开裂，材料的断裂转变成剪切断裂，并形成剪切断口。有限元分析结果与实验结果接近。这一结果说明板料在拉伸过程中，具有很强的非线性。图8和图9分别说明了修正的GTN-Hill1948细观损伤模型能够有效地预测板料的载荷能力和描述失效演化过程的能力，进一步证明所标定的损伤参数的正确性。

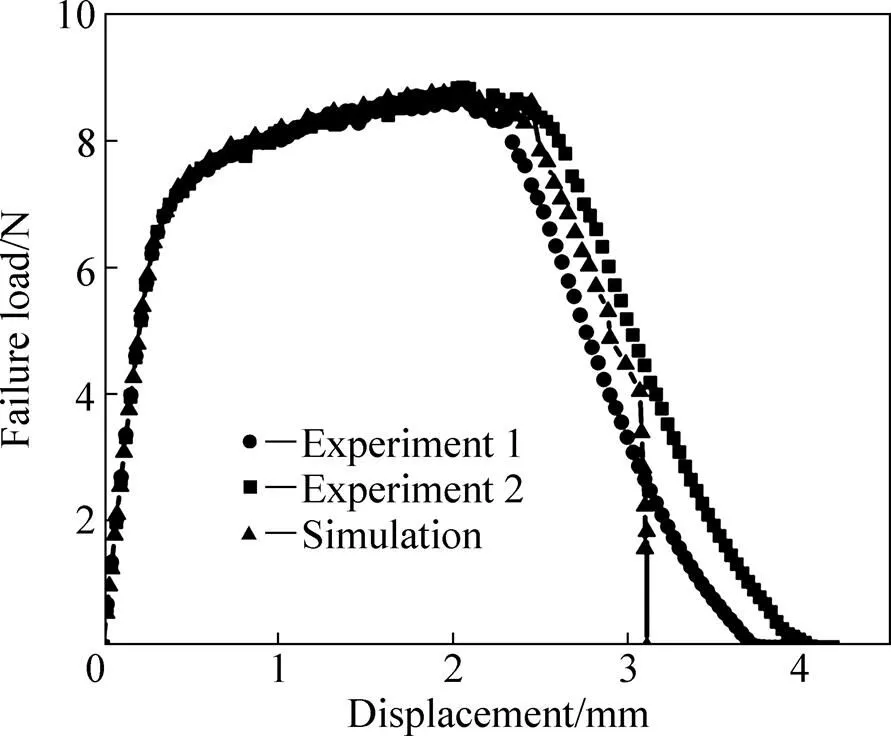
图8 带孔洞验证试样的载荷−位移曲线

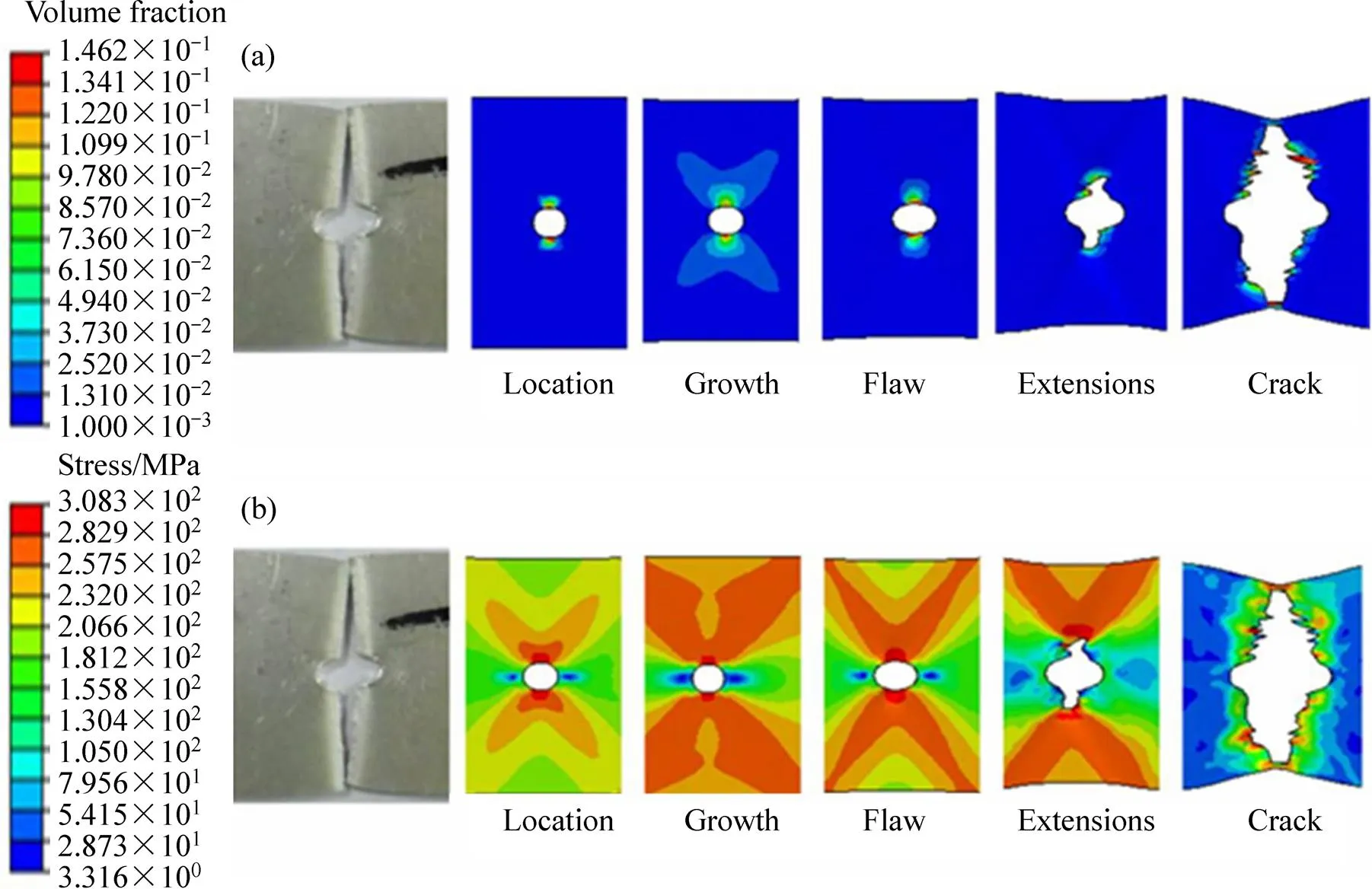
图9 中间带孔验证试样的失效演化过程

4 结论

1) 基于设计的带凹槽的试样和剪切试样，通过反向优化法获得了Al6061板材的GTN-Hill1948 损伤参数：0=0.0005，k=2。

2) 通过中心带孔的拉伸试样验证了GTN-Hiill1948所标定参数的正确性，并且该细观损伤模型能够有效地预测板料的载荷能力和失效能力。

REFERENCES

[1] 李永兵, 李亚庭, 楼 铭, 林忠钦. 轿车车身轻量化及其对连接技术的挑战[J]. 机械工程学报, 2012, 48(18): 44−54. LI Yong-bing, LI Ya-ting, LOU Ming, LIN Zhong-qin. Light weighting of car body and its challenges to joining technologies[J]. Chinese Journal of Mechanical Engineering, 2012, 48(18): 44−54.

[2] 关绍康, 姚 波, 王迎新. 汽车铝合金车身板材的研究现状及发展趋势[J]. 机械工程材料, 2001, 25(5): 12−14. GUAN Shao-kang, YAO Bo, WANG Ying-xin. The progress and prospect of research on aluminium alloys for auto body sheets[J]. Materials for Mechanical Engineering, 2001, 25(5): 12−14.

[3] 汤安民, 师俊平.铝合金材料剪切断裂实验分析[J]. 力学季刊, 2002, 23(1): 82−86. TANG An-min, SHI Jun-ping. Experiment analysis for shear break of aluminum alloy material[J]. Chinese Quarterly of Mechanics, 2002, 23(1): 82−86.

[4] 黄建科. 金属成形过程的细观损伤力学模型及韧性断裂准则研究[D]. 上海: 上海交通大学, 2009: 17−34. HUANG Jian-ke. Study on meso-damage model and ductile fracture criterion in metal forming processes[D]. Shanghai: Shanghai Jiao Tong University, 2009: 17−34.

[5] 蒲思洪, 温 彤, 吴 维, 侯模辉. 韧性断裂准则与阀值选取的理论及试验研究[J]. 热加工工艺, 2009, 38(3): 18−21. PU Si-hong, WEN Tong, WU Wei, HOU Mo-hui. Theoretical and experimental research on choosing criterion and critical value of ductile fracture[J]. Hot Working Technology, 2009, 38(3): 18−21.

[6] QUAN Guo-zheng, WANG Feng-biao, LIU Ying-ying, SHI Yu，ZHOU Jie. Evaluation of varying ductile fracture criterion for 7075 aluminum alloy[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(3): 749−755.

[7] ZHANG D F, DAI Q W, LIN F. XU X X. Prediction of edge cracks and plastic-damage analysis of Mg alloy sheet in rolling[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(5): 1112−1117.

[8] GURSON A L. Plastic flow and fracture behavior of ductile materials incorporating void nucleation, growth, and interaction[D]. Kongens Lyngby: The Technical University of Denmark, 1975: 67−80.

[9] TVERGAARD V，NEEDLEMAN A. Analysis of the cup-cone fracture in a round tensile bar[J]. Acta Metallurgica, 1984, 32(1): 157−169.

[10] 王 涛, 庄新村, 赵 震. GTN模型的现状与发展[C]//第十三届全国塑性工程学术年会暨第五届全球华人塑性技术研讨会论文集. 北京: 塑性工程学会, 2013: 61-64. WANG Tao, ZHUANG Xin-cun, ZHAO Zhen. The present situation and development of GTN model[C]//The 13th Annual Meeting and the Fifth World Chinese National Plastic Engineering Academic Symposium on Plastic Technology. Beijing: China Society for Technology of Plasticity, 2013: 61−64.

[11] 王明正, 李晓延. TC4 钛合金GTN 损伤模型反向标定法研究[J]. 稀有金属材料与工程, 2012,41(5): 795-799. WANG Ming-zheng, LI Xiao-yan. Study on GTN damage model of TC4 titanium alloy by an inverse approach[J]. Rare Metal Materials and Engineering, 2012, 41(5): 795-799.

[12] 石柏军, 彭 松, 刘松林, 王叶青. 基于 GTN 损伤模型的压力连接过程有限元仿真[J]. 材料科学与工艺, 2012, 20(2): 86−89. SHI Bai-jun, PENG Song, LIU Song-lin, WANG Ye-qing. Simulation analysis of the mechanical clinch joining process based on the GTN model[J]. Materials Science and Technology, 2012, 20(2): 86−89.

[13] ZHAO S D，XU F，GUO J H，HAN X L. Experimental and numerical research for the failure behavior of the clinched joint using modified Rousselier model[J]. Journal of Materials Processing Technology, 2014, 214(10): 2134−2145.

[14] 朱 浩, 芳娟齐, 张 洋. 剪应力状态下 6061 铝合金的力学性能及断裂行为[J]. 中国有色金属学报, 2015, 22(6): 1570−1576. ZHU Hao, QI Fang-juan, ZHANG Yang. Mechanical properties and fracture behavior of 6061 aluminum alloy under shear stress states[J]. The Chinese Journal of Nonferrous Metals, 2015, 22(6): 1570−1576.

[15] 叶 拓, 王 冠, 姚再起, 李落星. 汽车用 6xxx 系铝合金薄壁件的韧性断裂行为[J]. 中国有色金属学报, 2015, 24(4): 878−887. YE Tuo, WANG Guan, YAO Zai-qi, LI Luo-xing. Ductile fracture behavior of 6xxx aluminum alloy thin-walled components of automobile[J]. The Chinese Journal of Nonferrous Metals, 2015, 24(4): 878−887.

[16] NAHSHON K，XUE Z Y. A modified Gurson model and its application to punch-out experiments[J]. Engineering Fracture Mechanics, 2009, 76(8): 997−1009.

[17] NAHSHON K，HUTCHINSON J W. Modification of the Gurson model for shear failure[J]. European Journal of Mechanics-A/Solids, 2008, 27(1): 1−17.

[18] GULLERUD A S, GAO X S, DODDS R H Jr, HAJ-ALI R. Simulation of ductile crack growth using computational cells: Numerical aspects[J]. Engineering Fracture Mechanics, 2000, 66(1): 65−92.

[19] YOUNISE B, SEDMAK A, RAKIN M, GUBELJAK N, MEDJO B, BURZIĆ M, ZRILIĆ M. Micromechanical analysis of mechanical heterogeneity effect on the ductile tearing of weldments[J]. Materials & Design, 2012, 37: 193−201.

[20] YAN Y X, SUN Q, CHEN J J, PAN H L. The initiation and propagation of edge cracks of silicon steel during tandem cold rolling process based on the Gurson−Tvergaard−Needleman damage model[J]. Journal of Materials Processing Technology, 2013, 213(4): 598−605.

[21] ACHOURI M, GERMAIN G, SANTO P D, SAIDANE D. Numerical integration of an advanced Gurson model for shear loading: Application to the blanking process[J]. Computational Materials Science, 2013, 72(9): 62−67.

[22] XUE Z Y，FALESKOG J，HUTCHINSON J W. Tension–torsion fracture experiments−Part II: Simulations with the extended Gurson model and a ductile fracture criterion based on plastic strain[J]. International Journal of Solids and Structures, 2013, 50(25): 4258−4269.

[23] ROUSSELIER G. Ductile fracture models and their potential in local approach of fracture[J]. Nuclear Engineering and Design, 1987, 105(1): 97−111.

[24] ROUSSELIER G. Dissipation in porous metal plasticity and ductile fracture[J]. Journal of the Mechanics and Physics of Solids, 2001, 49(8): 1727−1746.

[25] FALESKOG J，GAO X S，SHIH C F. Cell model for nonlinear fracture analysis−I. Micromechanics calibration[J]. International Journal of Fracture, 1998, 89(4): 355−373.

[26] LUO M，DUNAND M，MOHR D. Experiments and modeling of anisotropic aluminum extrusions under multi-axial loading−Part II: Ductile fracture[J]. International Journal of Plasticity, 2012, 32: 36−58.

[27] HE Min, LI F G, WANG Z G. Forming limit stress diagram prediction of aluminum alloy 5052 based on GTN model parameters determined by in situ tensile test[J]. Chinese Journal of Aeronautics, 2011, 24(3): 378−386.

[28] GUO J H，ZHAO S D，MURAKAMI R，ZANG S. Experimental and numerical investigation for ductile fracture of Al-alloy 5052 using modified Rousselier model[J]. Computational Materials Science, 2013, 71: 115−123.

[29] 赵彦玲, 车春雨, 云子艳, 王弘博, 铉佳平, 张广洲. GTN 细观损伤模型在铝合金轧制裂边分析中的应用[J]. 哈尔滨理工大学学报, 2014, 19(4): 44−48. ZHAO Yan-ling, CHE Chun-yu, YUN Zi-yan, WANG Hong-bo, XUAN Jia-ping, ZHUANG Guang-zhou. Application of GTN-micromechanical damage model in analysis of rolling edge crack defects[J]. Journal of Harbin University of Science and Technology, 2014, 19(4): 44−48.

(编辑 何学锋)

Modified GTN-Hill1948 damage model of Al6061 panel

HAN Xiao-lan1, ZHAO Sheng-dun1, XU Fan1, CHEN Chao1, ZHAO Ren-feng2

(1. Molding and Advanced Forming Technology, School of Mechanical Engineering,Xi’an Jiaotong University, Xi’an 710049, China;2. School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China)

In order to obtain the parameters of the GTN-Hill1948 damage model, a specimen with a notch and a shear specimen of Al6061 panel were designed to get the load-displacement curves. Based on the ABAQUS software, the corresponding model of the specimens was built. The material parameters, void volume fraction andshear damage coefficient of the model were identified by an inverse method, comparing the experimental results with the numerical results. And to verify the correctness of the two parameters, the specimen with a hole was designed. The results show that theinitial void volume fraction is 0.0005 and the shear damage coefficient is 2, which are determined by the inverse method. The GTN-Hill1948 damage model can predict the failure location of Al6061 panel.

Al 6061 panel; GTN-Hill1948 damage model; damage evolution; inverse method

Project(51675414) supported by the Major Program of the National Natural Science Foundation of China; Project(2009ZX04005-031) supported by the National Science and Technology Major Project, China; Project(2011KTCQ01-04) supported by the Coordinated Innovation Programs of Science and Technology of Shaanxi Province, China

2015-09-18; Accepted date: 2016-05-13

ZHAO Sheng-dun; Tel: +86-29-82668607; E-mail: hanxiaolang007@163.com

10.19476/j.ysxb.1004.0609.2017.05.004

1004-0609(2017)-05-0902-09

O346.5

A

国家自然科学基金面上项目(51675414)；国家重大科技专项(2009ZX04005-031)；陕西省科技统筹创新工程计划资助项目(2011KTCQ01-04)

2015-09-18；

2016-05-13

赵升吨，教授，博士；电话：029-82668607；E-mail：hanxiaolang007@163.com