崩落法回采巷道顶板危险区域确定的解构法和数值模拟法

陈庆发，牛文静，郑文师，刘俊广，刘严中，尹庭昌



崩落法回采巷道顶板危险区域确定的解构法和数值模拟法

陈庆发1，牛文静1，郑文师1，刘俊广1，刘严中2，尹庭昌1

(1. 广西大学资源与冶金学院，南宁 530004；2. 中南大学资源与安全工程学院，长沙 410083)

在铜坑矿92号矿体裂隙矿岩崩落法开采区域选取试验区，阐述崩落法回采过程巷道顶板危险区域确定的解构法和数值模拟法的具体内涵，对两种方法计算结果及差异性进行分析比较。结果表明：解构法能够准确解算危险结构体可能失稳的形式和具体赋存位置，但其从矢量角度确立的危险结构体数量、危险区域分布范围比真实情况略小，巷道稳定性结果略高；数值模拟法考虑卸荷和爆破作用影响，对回采过程顶板下沉、结构体失稳状态分析较准确，但采用虚拟裂隙面控制结构面发育范围，导致确立的危险结构体数目过多，巷道稳定性比工程实际略低；工程应用中应以解构法为主、数值模拟法为辅，综合确定巷道顶板危险区域。

巷道顶板；危险区域；解构法；数值模拟法；崩落法开采

崩落法具有开采强度大、工程量少、成本低等优点，我国地下铁矿山应用崩落法采出的矿量超过85%，有色金属矿山超过35%[1]。但因采用崩落法开采时采场巷道维护困难，导致其应用难度较大。裂隙矿岩崩落法开采时，受卸荷、爆破等采动作用影响，回采巷道顶板常发生不同形式失稳，以至常规安全控制措施因无针对性而常出现失效现象。因此，在崩落法回采条件下，准确预测巷道顶板危险区域对矿体安全回采、巷道针对性支护具有重要影响。

目前，已有部分学者开展了巷道顶板稳定性相关研究，具代表性的有：SEEDSMAN[2]针对回采过程巷道顶板应力变化和失稳路径分析了巷道顶板失稳机理；NEMCIK等[3]基于多滑动块体模型，通过计算和分析顶板块体间相互作用及应力变化，提出了巷道顶板破坏机制；牛少卿等[4]针对煤层巷道顶板层状特征，利用梁受力变形原理和岩体粗糙结构面剪胀原理，分析了大跨度巷道顶板层面剪切失稳机理；曾佑富等[5]利用弹性力学和数值模拟方法，对枣泉煤矿巷顶板冒落失稳机理进行了分析；陶干强等[6]利用数值模拟方法，对开拓与回采两个不同过程巷道顶板稳定性进行了分析；眀建等[7]针对崩落法回采条件下巷道顶板冒落特征，开展了巷道围岩变形机理研究；HU等[8]通过对崩落法回采顶板最大拉应力、下沉位移、等效塑性应变等的研究，开展了巷道顶板岩体卸荷力学响应规律研究；赵毅鑫等[9]引入扰动因子概念分析了多扰动状态下回采巷道的稳定性。但有关裂隙矿岩崩落法回采巷道顶板结构体移动形式及稳定性的研究还鲜见报道，致使矿体回采过程中的巷道顶板危险结构体及危险区域的变化状态尚不能较好确定。

因此，本文作者分别利用岩体结构解构理论和数值模拟方法，开展巷道顶板危险区域确定的解构法和数值模拟法比较分析研究，通过对比分析两种方法，建立准确可靠的崩落法回采巷道顶板危险区域确定方法，以期为支护措施设计提供根本性指导。

1 巷道顶板危险区域确定方法

1.1 岩体结构解构法

解构概念源于海德格尔[10]提出的“Deconstruction”一词，意为对事物进行分解、消解、拆解、揭示等。本文作者基于地下矿山工程背景，引入“解构”思想，提出“岩体结构解构”，即将岩体结构重构，揭示结构单元在岩体内部的三维排列组合形式，并结合具体采矿工艺，对采矿活动过程中的结构体的移动性进行分析，稳定性进行计算，以分析与计算结果为依据，及时、合理、科学的调整与优化开采工艺，实施积极的先导技术措施，从而指导矿体安全回采[11−12]。

利用岩体结构解构理论确定崩落法回采过程中巷道顶板危险区域的总体思路为：基于关键块体理论、一般块体理论、岩石力学和材料力学等知识，利用GeneralBlock软件对块体的识别与计算的功能和3DMine软件的空间计算与三维可视化的功能，对崩落法开采条件下的巷道围岩结构进行初步解构；对初步解构出的结构体位置及最小固定面积进行计算；结合具体回采工艺，分析回采过程中赋存于巷道顶板结构体的移动性，确立危险结构体；根据危险结构体分布范围，确定巷道顶板危险区域。

1.2 数值模拟法

数值模拟作为当代科学研究的第三种手段，具有较强优越性[13]。矿山领域利用数值模拟手段可模拟各类采矿方法，并分析回采过程中的科学问题。

利用数值模拟方法确定崩落法回采过程中巷道顶板危险区域的思路为：通过GeneralBlock软件与3DEC软件的参数对接，将GeneralBlock软件构建的巷道围岩结构体模型与3DEC模型耦合，形成3DEC巷道围岩结构体模型；利用3DEC软件计算功能，以静力和动力结合方式模拟崩落法回采，监测回采过程中巷道顶板下沉量和结构体运动状态；通过分析不同回采阶段结构体运动状态，确立回采过程中巷道顶板危险区域及危险结构体。

2 解构理论确定巷道顶板危险区域

2.1 工程背景

铜坑矿92号矿体产出于长坡铜坑矿床下部，水平方向上位于207号线至210号线之间，垂直方向上位于+250~+580 m标高范围内，埋藏深度在+250~+450 m间，节理裂隙极为发育，采用无底柱分段崩落法回采。选取极具代表性且结构面较发育的+494 m水平T214采场的14号出矿川为试验区，开展相关研究，如图1所示。

试验区内岩层近东西走向，受以节理和褶皱为主的构造影响，岩层倾向及倾角变化较大。试验区巷道岩石坚硬、性脆，岩层较干燥、破碎。试验区岩体总体较破碎，常出现浮石，采动来压后易出现规模较大掉块现象。利用精测网法测出试验区内共赋存有535条结构面，二维密度为7.23条/m2，平均间距为37.38 mm。试验区内结构面主要由80%的压性层理面和20%的张扭性节理构成，且按倾向分为4组，第1组10°~20°、第2组30°~40°、第3组280°~290°、第4组300°~310°，其中，第1、2组为优势组。试验区内岩体的抗压强度为81.26 MPa，抗剪强度8.572 MPa，容重2.68 t/m3，内聚力为2.5 MPa，内摩擦角为30°。试验区巷道长20 m、宽3.7 m、高2.8 m，崩落法回采时，沿巷道轴向后退式回采，崩矿步距为5 m，共分5步回采。

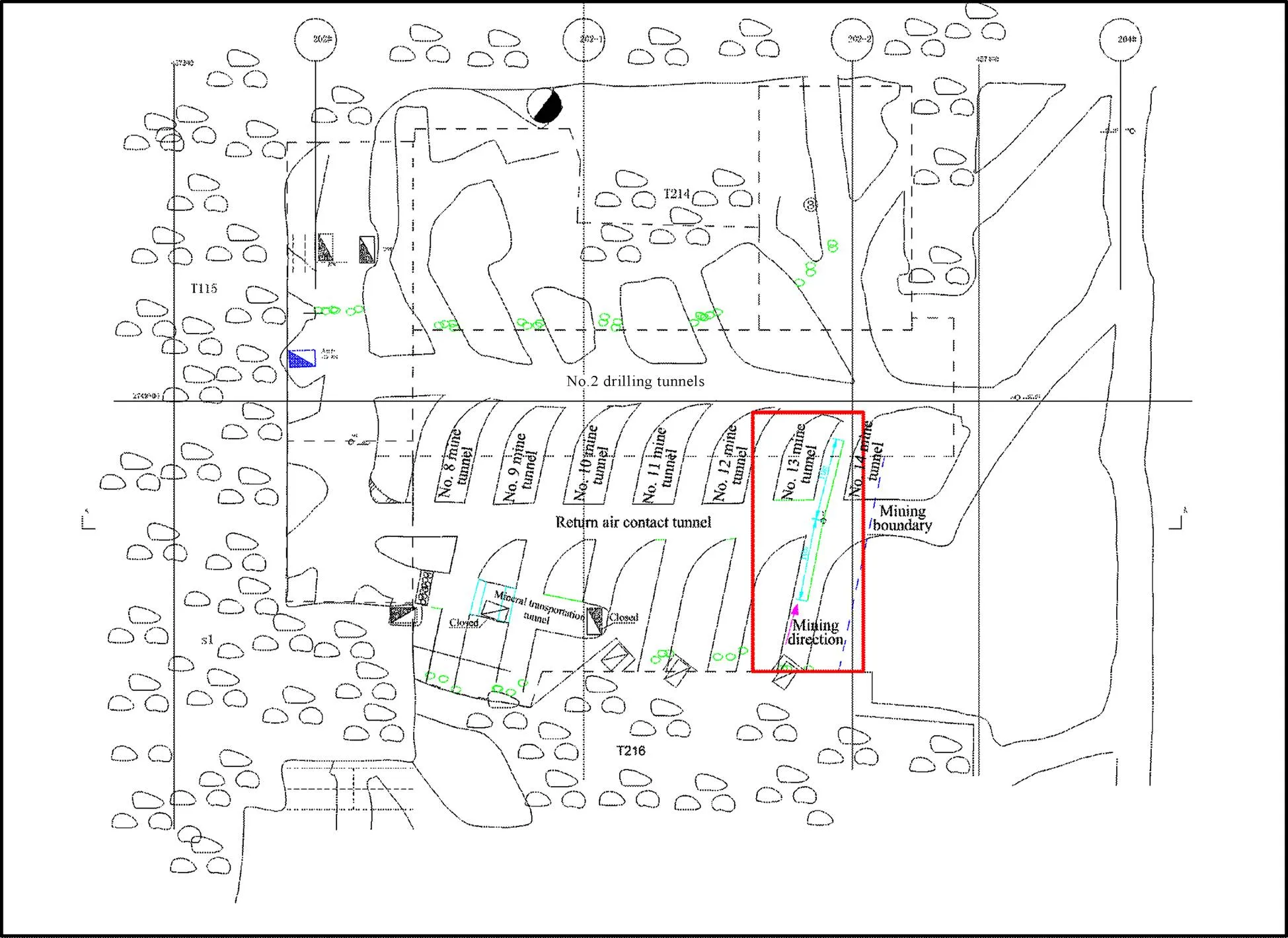
图1 试验区示意图

2.2 巷道顶板结构体解构

试验区巷道长宽高尺寸为20 m×3.7 m×2.8 m，为使构建的巷道围岩模型包裹大部分结构面，且各结构面在巷道围岩内充分地交错、切割，利用GeneralBlock软件建立长宽高尺寸为20 m×20 m× 22 m的围岩模型，如图2所示。模型的轴沿巷道宽度方向，轴方向为巷道走向，轴沿巷道高度方向。将结构面调查数据输入巷道围岩模型中，构建巷道围岩结构体模型，并利用GeneralBlock软件的计算功能对巷道顶板结构体进行初步解构。初步解构内容主要有巷道顶板结构体编号、类型、体积、稳定性系数、滑移面、下滑力、摩擦力和粘滞力等。

初步解构出试验区巷道顶板共赋存179个结构体，其中可移动结构体88个、不可移动结构体7个、埋藏结构体45个、固定结构体39个，如图3所示。块体理论一般认为固定结构体和埋藏结构体是稳定的，不进行移动性分析。但受矿体回采工作扰动，固定结构体和埋藏结构体也可能产生移动，进而对矿体正常开采产生不良影响。因此，需对初步解构的固定结构体和埋藏结构体进一步解算。

图2 试验区巷道围岩模型

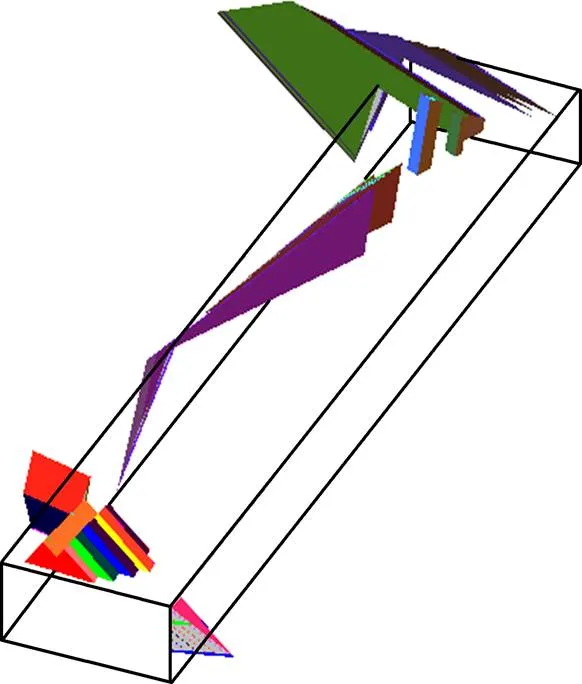
图3 巷道顶板结构体初步解构

2.3 结构体位置与最小固定面积计算

将利用GeneralBlock软件解构出的结构体导入3DMine软件中，利用3DMine软件的三维计算功能，解算结构体的空间形态、固定面面积、重心坐标、形心坐标等参数。

固定结构体实为无限结构体，但受自身重力或其他工程扰动作用，固定面可能发生破坏，进而可能导致结构体移动并失稳。因此，存在一个最小面积的固定面，使得结构体恰好维持自身稳定，该面积称为结构体的最小固定面积[11]。当结构体固定面面积大于其最小固定面积时，该结构体稳定性较好；当小于其对应的最小固定面积时，结构体固定面可能发生破坏。显然，埋藏结构体的最小固定面积为0。由文献[11]的最小固定面积(min)计算公式，对单固定面结构体的最小固定面积进行计算，结果如表1所示。

由表1可知，39个固定结构体中，有27个结构体因其固定面积小于对应的最小固定面积而可能产生固定面被破坏的现象。因此，需进一步分析此类结构体的回采可移动性。

2.4 回采过程中结构体移动性分析

回采前，出露于巷道顶板表面的固定面积小于其对应最小固定面积的结构体，受重力影响或其他工程扰动作用，固定面可能被破坏，进而产生移动；回采过程中，矿岩受回采工作面切割，位于回采工作面周围的结构体将被切割，进而移动性可能发生变化，即回采前不可移动的结构体，受回采作用影响可能产生移动。因此，回采过程中应结合矿体回采步距，对每步回采后结构体变化情况进行分析。利用矢量方法，分回采前和回采过程两个阶段开展巷道顶板结构体可移动性分析。

设存在一个结构体，具有个结构面、个固定面，结构面指向结构体内部的单位法向矢量为，固定面指向结构体内部的单位法向矢量为，重力单位方向矢量为，如图4所示。只考虑重力作用时，若∙≥0，则面不对重力方向的移动产生阻碍，即为非重力约束面；若∙＜0，则面几何上对结构体重力方向的移动产生阻碍，即为重力约束面。令重力约束面交线指向结构体内部的位矢为，临空面指向下方的位矢为，临空面的相邻面指向临空面方向的位矢为，则

1) 当临空面的相邻面无重力约束面时，结构体掉落；

2) 当临空面的相邻面同时存在重力约束面和非重力约束面，且重力约束面满足∙≥0时，结构体沿重力约束面单面滑动；

3) 当临空面的相邻面同时存在重力约束面和非重力约束面，且重力约束面的交线与各结构面的法向量满足∙≥0时，结构体沿重力约束面交线滑动(双面滑动)；

4) 当临空面的相邻面既有非重力约束面又有重力约束面，且重力约束面满足∙＜0时，结构体不可产生移动。

1) 回采前结构体移动性分析

回采前，试验区内27个固定面易被破坏的固定结构体中，有25个出露于巷道表面，因此，对此25个结构体进行移动性分析。

①掉落：结构体164和165除固定面外，其余面均为非重力约束面。当固定面破坏时，临空面的相邻面均为非重力约束面，因而，此2个结构体可能直接掉落。

②单面滑动：结构体171和179固定面被破坏后，临空面相邻面即有重力约束面又有非重力约束面，且重力约束面位矢与临空面位矢满足∙≥0，因而，此两个结构体可能沿重力约束面单面滑动。

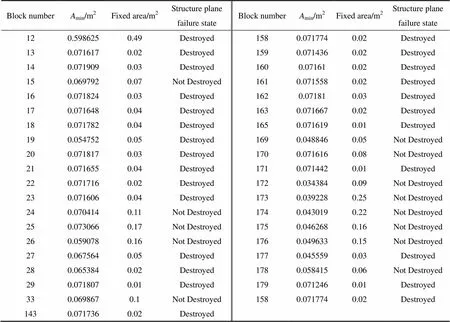
表1 结构体最小固定面积计算结果

③双面滑动：结构体13、14、16、17、18、19、20、22、23、27、28、29、143、158、159、160、161、162和163固定面被破坏后，临空面的相邻面即有重力约束面又有非重力约束面，且重力约束面的交线与各结构面的法向量满足∙≥0，因而，此20个结构体可能沿重力约束面交线双面滑动。

④不可移动：结构体177固定面被破坏后，临空面的相邻面即有重力约束面又有非重力约束面，但重力约束面法向矢量与临空面法向矢量满足∙＜0，故结构体固定面破坏后仍不可移动。

通过上述结构体移动性分析可知，回采前，出露于巷道表面的25个固定结构体中，可能掉落的结构体有2个，单面滑动的结构体有2个，双面滑动的结构体有20个，不可移动的结构体有1个。

2) 回采过程中结构体移动性分析

试验区共分5步回采，以轴为回采方向，回采界面分别位于巷道围岩模型的=0 m、=5 m、=10 m、=15 m和=20 m处。

①第1步回采时，位于回采工作面附近的不可移动结构体有169、170、172、173、174、175、176和178，对其分别进行移动性分析。

结构体169、170、175、176和178均由2个重力约束面和2个非重力约束面构成，临空面相邻面既有重力约束面又有非重力约束面，且满足∙≥0，此5个结构体将沿重力约束面交线滑动。

结构体172、173和174均由3个重力约束面和3个非重力约束面构成，临空面的相邻面既有重力约束面又有非重力约束面，且满足∙≥0。因此，此3个结构体沿重力约束面交线双面滑动。

②第2步回采、第3步回采和第4步回采时，回采面附近没有新结构体生成；第5步回采时，整个试验区已被回采，无需开展结构体移动性分析。

通过对回采过程中结构体移动性分析可知，受回采作用影响，将可能有8个出露于巷道顶板的原本不可移动结构体产生滑动。

2.5 试验区巷道顶板危险区域显现与确定

综合试验区巷道顶板结构体初步解构结果、回采前结构体移动性分析结果和回采过程结构体移动性分析结果，确立崩落法回采巷道顶板危险结构体。最终确定赋存于巷道顶板可能掉落的结构体有两个，产生单面滑动的结构体有22个，产生双面滑动的结构体有96个。因此，试验区巷道顶板共有120个危险结构体。将各危险结构体在GeneralBlock软件中筛选，并导入3DMine软件中，三维显现结构体在巷道顶板的分布范围及形态，如图4所示。

根据巷道顶板结构体解构结果可知，崩落法回采下试验区巷道顶板危险结构体数量较多，但体积相对较小，分布范围较广。由图4中危险结构体分布范围，确定出崩落法回采过程中巷道顶板的危险区域(图中矩形线框区域为巷道顶板危险区域)。

危险区域集中在轴方向上0~3 m和12~20 m范围。根据巷道顶板危险结构体数量和危险区域分布范围可判断巷道顶板较易失稳，该结论较符合巷道实际调查情况。

图4 试验区结构体和危险区域三维显现图

3 数值模拟确定巷道顶板危险区域

3.1 参数选择及数值模型构建

1) 力学参数选择

①静力分析参数选择

92号矿体上部地表标高+800 m，试验区岩体密度为2.68 t/m3，侧压系数分别为1.5和1.4。参考强度折减法[14]，试验区模型上覆岩层等效载荷为，则侧压为和。经计算，试验区为5.93 MPa、为5.53 MPa、为3.95 MPa。

根据地质调查和物理实验确定模型体积模量为1.10×104MPa、剪切模量为1.15×104MPa、弹性模量为2.85×104MPa、泊松比为0.24、抗拉强度为2.1 MPa。根据矿山提供的结构面力学参数研究报告确定试验区结构面模型力学参数，如表2所列。

根据Kulatilake提出的虚拟裂隙面力学参数取值方法[15]，计算虚拟裂隙面力学参数，具体如表3所列。

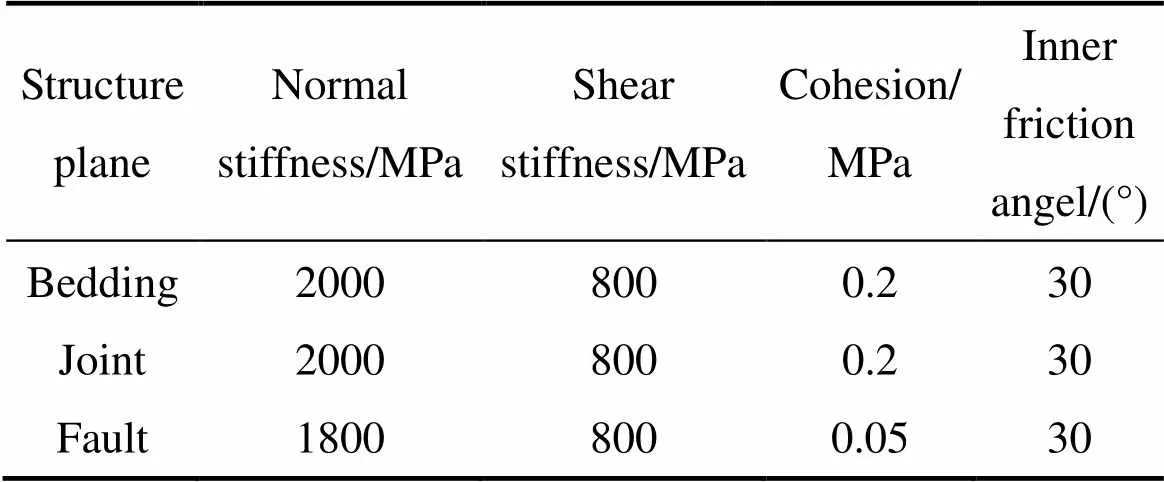
表2 试验区结构面模型参数表

表3 虚拟裂隙面力学参数表

②动力分析参数选择

动力分析采用Rayleigh阻尼，且为有效增加计算精度，动力分析过程中，仅考虑刚度阻尼比作用，忽略质量阻尼比[16]。为减少模型边界波反射，降低反射波对模拟结果的影响，将试验区巷道围岩模型4个侧面和底面设置为粘滞边界。依据铜坑矿92号矿体爆破震动危害研究，确立了动力分析所需相关爆破数据，主要为爆破震动主频37 Hz、最大振速49.9 mm/s、最大位移19.8×10−2 mm。

2) 数值模型构建

开挖卸荷导致应力重分布，其影响范围为20~30 m[17]。为便于研究，3DEC数值模型需在建立的GeneralBlock解构模型基础上适量增加尺寸，且数值模型坐标与解构模型坐标保持一致。结合巷道实际长度、回采步距和影响范围，最终确定试验区巷道围岩模型长宽高尺寸为110 m×100 m×22 m。

3DEC软件中默认结构面无限大，各类贯穿于整个模型的结构面将模型切割为各类不同结构体。但工程实际中，岩体不仅含有大规模贯穿性结构面，也发育有规模相对较小的非贯穿性结构面。为准确确定虚拟裂隙面位置坐标，利用GeneralBlock软件迹线三维显现功能，采用逐步逼近法确定巷道围岩结构体模型中裂隙组发育范围。虚拟裂隙面位置的具体确定过程为：逐步显示结构面迹线在垂直于、、3个坐标轴的二维裂隙网络显现图，使结构面迹线恰好不在二维裂隙网络图上显示，此时的、、坐标值即为虚拟裂隙面位置坐标。

利用3DEC的模型构建功能，根据确定的模型尺寸，构建包含调查结构面及虚拟结构面的试验区巷道围岩结构体数值计算模型，如图5所示。

图5 试验区3DEC数值模型

3.2 崩落法回采过程模拟

考虑爆破作用与开挖卸荷作用的共同影响，采用动力和静力结合的方式，按回采步距分步对试验区进行崩落法回采模拟。在回采过程中，先将爆破震动速度时程曲线转化为应力时程曲线，在回采工作面以简谐正弦波的形式施加动载荷模拟爆破震动作用[18]，然后再进行开挖卸荷作用的静力分析。每步回采依次循环上述过程，直至完成整个试验区的回采模拟。

模拟崩落法回采过程中，在巷道顶板向上0.1 m位置处布设监测面(即=2.9 m平面)，监测每步回采后巷道顶板受回采作用的方向位移变化情况。

3.3 数值分析确定危险区域

基于回采过程中监测的巷道顶板=2.9 m平面在方向的位移量，参考前人研究成果[19]，以顶板下沉量0.05 m为准，确立巷道顶板危险区域，即巷道顶板下沉量大于0.05 m的区域为危险区域。根据不同回采步骤的顶板下沉量大于0.1 m区域的坐标范围，确立巷道顶板危险区域分布范围。

试验巷道位于巷道围岩结构体模型的轴方向的0~20 m区域范围，崩矿步距为5 m，以边界=−10 m为起始位置模拟开挖，分5步回采。每步回采结束后，分析未回采巷道顶板的下沉量。由于第5步回采后，整个试验区巷道已被回采完毕，因而，只对前5步回采结束后的未回采巷道顶板下沉量进行监测分析。每步开采结束后，顶板下沉量如图6所示。

由图6可知，第1步回采结束后，巷道顶板危险区域为轴方向2.5~5 m和15~23.6 m范围；第2步回采结束后，巷道顶板危险区域为方向15~22.9 m范围；第3步回采结束后，巷道顶板危险区域为轴方向15~22.7 m范围；第4步回采结束后，巷道顶板危险区域为轴方向15~22.5 m范围。由于试验区巷道在轴方向仅20 m，因此，对巷道顶板在整个回采过程中的危险区域求并集，确立2.5~5 m和15~20 m范围为巷道顶板的危险区域。

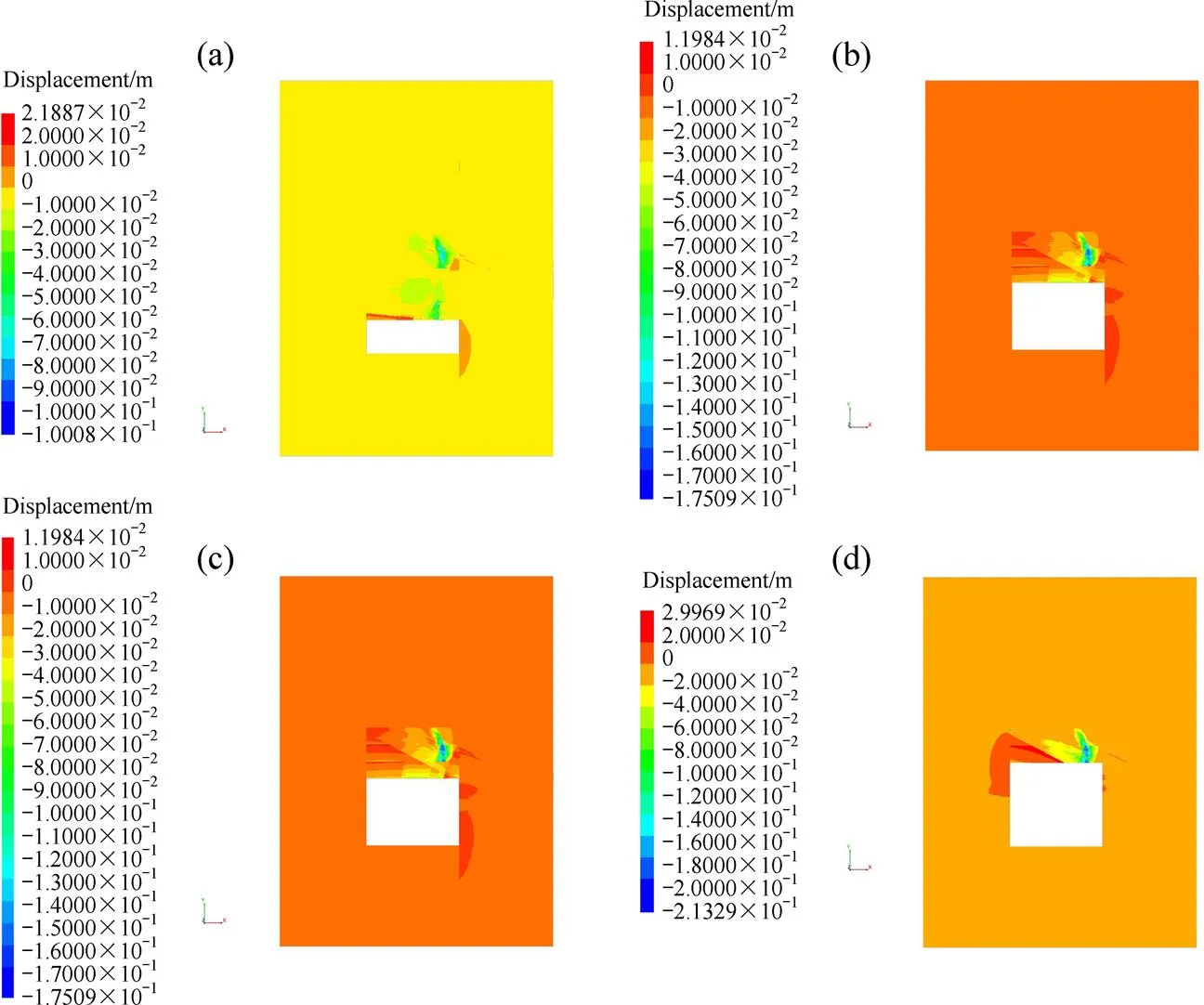
图6 巷道顶板位移云图

3.4 巷道顶板危险区域显现

为便于与解构法确立的危险区域比较，对数值模拟法确立的危险区域内的结构体移动状态进行监测，分析结构体失稳状态，显现危险结构体分布形态及危险区域分布范围，如图7所示。

图7 危险区域数值模拟结果

由图7可知，崩落法回采过程中，试验区危险结构体数量较多，但体积较小，危险区域内的巷道顶板较破碎。

4 解构法与数值模拟法的结果

4.1 危险区域分布范围及危险结构体

对裂隙岩体崩落法开采巷道顶板危险区域解构理论确定结果和数值模拟方法确定结果进行比较，分析两种方法确立的危险结构体规模及危险区域分布范围。

解构法确定出巷道顶板危险结构体分布范围广、数量多、体积规模小，危险区域分布在轴方向0~3 m和12~20 m处；数值模拟法确定出巷道顶板危险结构体分布范围较集中、数量较多、体积规模小，危险区域分布在轴方向2.5~5 m和15~20 m处。对结果进行比较可知，应用岩体结构解构法确定的危险结构体数量与数值模拟法确立的结果有所差异，但两种方法对危险结构体分布范围的分析总体相近，且大部分范围重合。

利用岩体结构解构理论分析崩落法回采过程中结构体可移动性时，仅从矢量角度分析每步回采后位于回采工作面附近结构体的移动性变化，不能较好地分析赋存于未回采巷道围岩的结构体因卸荷和爆破作用影响的移动性变化，可能导致回采过程中增加的可移动性结构体较少的现象。故该方法确定的危险区域分布范围较数值模拟法相比较小。

数值模拟法确定巷道顶板危险区域时，以巷道围岩GeneralBlock模型为基础，利用3DEC软件以静力和动力结合方式模拟崩落法回采，并通过巷道顶板下沉量确立受卸荷与爆破作用影响下的巷道顶板危险区域。此外，通过监测危险区域内结构体的移动状态改变情况，确定危险性结构体。因而，该方法确定的危险区域分布范围较广，危险结构体数量较多。

4.2 结果的差异性

通过现场工程实际调查发现，试验区岩体总体较为破碎，常出现浮石。采动来压后，在试验区巷道两侧易出现规模较大的集中性掉块现象，掉落块体体积大多较小，存在个别块度较大的块体，如图8所示。将解构法、数值模拟法的计算结果与现场工程实际结果进行对比可知，解构法与数值模拟法均能得到与实际情况较符合的结论。

图8 巷道顶板破坏失稳现象

利用岩体结构解构理论确定崩落法回采过程中巷道顶板危险区域时，完全采用结构调查数据构建结构体模型，因而对岩体内部结构的解构结果较准确。但因未考虑卸荷及爆破作用，导致解构出的结构体数量与分布范围与真实情况相比略小，确立的巷道稳定性结果偏高。利用数值模拟手段确定崩落法回采过程中巷道顶板危险区域时，考虑了卸荷作用和爆破作用影响，使得对回采过程中顶板下沉状态、结构体失稳状态的分析比较准确。但该方法构建的3DEC模型采用虚拟裂隙面控制结构面发育范围，只控制了结构面在巷道走向方向的发育范围，仍会造成结构面发育范围与实际的差别，导致构建的模型内结构体数目过多，致使巷道稳定性比真实稳定性略低。故利用数值模拟法确定的巷道顶板危险区域结果一般偏大。

因此，两种确定巷道顶板危险区域的方法各具优缺点，但解构结果可得到危险结构体可能失稳形式和具体赋存位置，因而，解构法更具实用性。

4.3 巷道顶板危险区域综合确定

由于两种确定巷道顶板危险区域的方法各具优缺点，因此，在工程应用中，不能单一根据某一种结果确立，应以解构法确立的危险区域结果为主，以数值模拟分析结果为辅，综合确定巷道顶板的危险区域分布范围。

假设用集合1表示岩体结构解构法确定的崩落法开采巷道顶板危险区域，集合2表示数值模拟法确定的巷道顶板危险区域，如图9所示。则工程实际中，集合1和集合2的交集(即集合3)为最易发生失稳的区域，应重点采取安全措施。为确保回采工作的安全有效进行，保守起见，可选取1、2集合的并集作为采取安全支护措施的范围。

图9 顶板危险区域综合确定示意图

5 结论

1) 利用岩体结构解构方法，对崩落法开采条件下的巷道围岩结构进行了初步解构，对初步解构出的结构体位置及最小固定面积进行了计算，结合回采工艺分析了回采过程中巷道顶板结构体移动性，确立危险结构体，并根据危险结构体分布范围，确定巷道顶板危险区域。

2) 利用数值模拟方法，通过GeneralBlock软件与3DEC软件的参数对接，构建了3DEC巷道围岩结构体模型，以静力和动力结合方式模拟了崩落法回采，监测了回采过程中巷道顶板的下沉量，确立了回采过程中巷道顶板危险区域。

3) 通过对两种方法确立的危险区域分布范围及危险结构体结果的对比，从本质上分析了两种方法的差异性及优缺点，并提出了以解构法为主，以数值模拟法为辅的巷道顶板危险区域综合确定方法，研究成果能够有效指导巷道支护和采矿工艺优化。

REFERENCES

[1] 宋卫东, 王 欣, 杜建华. 程潮铁矿无底柱分段崩落法开采诱发地表变形规律[J]. 金属矿山, 2012, 46(7): 9−12. SONG Wei-dong, WANG Xin, DU Jian-hua. Surface deformation law of Chengchao iron mine induced by pillarless sublevel caving mining method[J]. Metal mine, 2012, 46(7): 9−12.

[2] SEEDSMAN R. The stress and failure paths followed by coal mine roofs during longwall extraction and implications to tailgate support[C]//20th International conference on ground control in mining. Morgantown: West Virginia University Press, 2001: 42−49.

[3] NEMCIK J A, PORTER I, INDRARATNA B. Stress analysis in failed roof at a longwall face[C]//Proceedings of the 17th Coal Congress of Turkey. Zonguldak: The Wollongong University Press, 2010: 193−202.

[4] 牛少卿, 杨双锁, 李 义, 贾喜荣. 大跨度巷道顶板层面剪切失稳机理及支护方法[J]. 煤炭学报, 2014, 39(z2): 325−331.NIU Shao-qing, YANG Shuang-suo, LI Yi, JIA Xi-rong. Shear instability mechanism and support methods of laminated roof and floor strata in roadway[J]. Journal of China Coal Society, 2014, 39(z2): 325−331.

[5] 曾佑富, 伍永平, 来兴平, 魏 成. 复杂条件下大断面巷道顶板冒落失稳分析[J]. 采矿与安全工程学报, 2009, 26(4): 423−427. ZENG You-fu, WU Yong-ping, LAI Xing-ping, WEI Cheng. Analysis of roof caving instability mechanism of large-section roadway under complex conditions[J]. Journal of Mining & Safety Engineering, 2009, 26(4): 423−427.

[6] 陶干强, 任青云, 罗 辉, 刘振东. 无底柱分段崩落法采场稳定性分析[J]. 岩土力学, 2011, 32(12): 3768−3779.TAO Gan-qiang, REN Qing-yun, LUO Hui, LIU Zhen-dong. Stability analysis of stope in pillarless sublevel caving[J]. Rock and Soil Mechanics, 2011, 32(12): 3768−3779.

[7] 明 建, 单 强, 严荣富. 自然崩落法采场软破围岩巷道支护技术研究[J]. 采矿与安全工程学报, 2014, 31(1): 34−40. MING Jian, SHAN Qiang, YAN Rong-fu. Study on supporting technology for roadways of soft rock mass in natural caving method[J]. Journal of Mining & Safety Engineering, 2014, 31(1): 34−40.

[8] HU Jian-hua, LEI Tao, ZHOU Ke-pin, LUO Xian-wei, YANG Nian-ge. Mechanical response of roof rock mass unloading during continuous mining process in underground mine[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2727−2733.

[9] 赵毅鑫, 姜耀东, 张科学, 王宏伟, 田素贵. 基于扰动状态理论的回采巷道稳定性分析[J]. 中国矿业大学学报, 2014, 43(2): 233−240. ZHAO Yi-xin, JIANG Yao-dong, ZHANG Ke-xue, WANG Hong-wei, TIAN Su-gui. Analysis of gate road stability in underground coal mining based on disturbed state theory[J]. Journal of China University of Mining & Technology, 2014, 43(2): 233−240.

[10] MARTIN HEIDEGGER. Being and Time, translated by J.macquarrie and E. Robinson[M]. Oxford: Basil Blackwell Publisher Ltd, 1985.

[11] 陈庆发, 赵有明, 陈德炎, 唐中琴, 于振宇. 采场内结构体解算及其稳定性计算[J]. 岩土力学, 2013, 34(7): 2051−2058. CHEN Qing-fa, ZHAO You-ming, CHEN De-yan, TANG Zheng-qin, YU Zhen-yu. Solution of structure body and its stability calculation in stope[J]. Rock and Soil Mechanics, 2013, 34(7): 2051−2058.

[12] 陈庆发, 韦才寿, 牛文静, 陈德炎, 冯春辉, 范秋雁. 一种基于块体化程度理论的裂隙岩体巷道顶板稳定性分级方法研究[J]. 岩土力学, 2014, 35(10): 2901−290. CHEN Qing-fa, WEI Cai-shou, NIU Wen-jing, CHEN De-yan, FENG Chun-hui, FAN Qiu-yan. Stability classification of roadway roof in fractured rock mass based on blockiness theory[J]. Rock and Soil Mechanics, 2014, 35(10): 2901−2907.

[13] 石耀霖, 周元泽, 张 怀, 王红才. 岩石圈三维结构与动力学数值模拟[J]. 地球学报, 2011, 32(z1): 125−135. SHI Yao-lin, ZHOU Yuan-ze, ZHANG Huai, WANG Hong-cai. Three-dimensional structure of the lithosphere and dynamic numerical simulation[J]. Acta Geoscientica Sinica, 2011, 32(z1): 125−135.

[14] 郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩土力学与工程学报, 2004, 23(19): 3381−3388. ZHENG Ying-ren, ZHAO Shang-yi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381−3388.

[15] KULATILAKE P H S W, UCPIRTI H, WANG S, RADBERG G, STEPHANSSON O. Use of the distinct element method to perform stress analysis in rock with non-persistent joints and to study the effect of joint geometry parameters on the strength and deformability of rock masses[J]. Rock Mechanics and Rock Engineering, 1992, 25(4): 253−274.

[16] Itasca Consulting Group. Three-dimensional distinct element code optional features[M]. Minneapolis: Itasca Consulting Group Inc, 2003.

[17] 钱鸣高, 石平五, 许家林. 矿山压力与岩层控制[M]. 徐州: 中国矿业大学出版社, 2011. QIAN Ming-gao, SHI Ping-wu, XU Jia-lin. Mining pressure and strata control[M]. Xuzhou: China Mining University Press, 2011.

[18] 王 洋, 叶海旺, 李延真. 裂隙岩体爆破数值模拟研究[J]. 爆破, 2012, 29(3): 21−22. WANG Yang, YE Hai-wang, LI Yan-zhen. Numerical simulation of jointed and fractured rock blasting[J]. Blasting, 2012, 29(3): 21−22.

[19] 岑传鸿. 顶板灾害防治[M]. 徐州: 中国矿业大学出版社, 1994. CEN Chuan-hong. Roof disaster prevention and control[M]. Xuzhou: China University of Mining and Technology Press, 1994.

(编辑 李艳红)

Deconstruction method and numerical simulation method of determination of tunnel roof’s dangerous area in caving stoping process

CHEN Qing-fa1, NIU Wen-jing1, ZHENG Wen-shi1, LIU Jun-guang1, LIU Yan-zhong2, YIN Ting-chang1

(1. College of Resources and Metallurgy, Guangxi University, Nanning 530004, China;2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The test area was selected in caving mining area of No. 92 ore body’s fracture ore rock at Tongkeng Minewas. The concrete connotation of the deconstruction method and numerical simulation method of determination of tunnel roof’s dangerous area in caving stoping process were described. The comparative analysis of calculation results and differences between these two methods was carried out. The results show that, firstly, the deconstruction method can accurately deconstruct the possible bulking forms and concrete occurrence positions of dangerous structural bodies. However, the number of dangerous structural bodies and the distribution range of dangerous area established by this method from aspects of vector are slightly smaller than real situation, and the results of roadway stability are slightly higher. Secondly, the numerical simulation method considers the influence of unloading and blasting action, so that it can more accurately analyze the roof subsidence and unstable states of structural bodies in stoping process. Nonetheless, it applies the virtual fracture surface to control the development range of structural planes, resulting in that the number of established dangerous structural bodies is excessive and the roadway stability is slightly lower than engineering practice. Thirdly, the deconstruction method should occupy dominant position, aided by the numerical simulation method, to comprehensively determine the dangerous area of roadway roof in engineering applications.

roadway roof; dangerous area; deconstruction method; numerical simulation method; caving mining method

Project(41402306) supported by Young Foundation of the National Natural Science of China; Project (2014GXNSFDA118034) supported by the Key Projects of Guangxi Province Natural Science Foundation, China; Project(14251011) supported by the Scientific Research & Technological Development Projects of Guangxi Province, China

2016-03-28; Accepted date: 2016-10-07

CHEN Qing-fa; Tel: +86-771-3232274; E-mail: chqf98121@163.com

10.19476/j.ysxb.1004.0609.2017.05.018

1004-0609(2017)-05-1006-10

TD853

A

国家自然科学基金资助项目(41402306)；广西自然科学基金重点项目(2014GXNSFDA118034)；广西科学研究与技术开发计划项目(桂科攻14251011)

2016-03-28；

2016-10-07

陈庆发，教授，博士；电话：0771-3232274；E-mail：chqf98121@163.com