Lu-F共掺杂ZnO光电性质的第一性原理计算

张明举，李文明，郑树凯



Lu-F共掺杂ZnO光电性质的第一性原理计算

张明举1, 2，李文明1, 2，郑树凯1, 2

(1. 河北大学电子信息工程学院，保定 071002；2. 河北大学计算材料与器件模拟研究中心，保定 071002)

采用基于密度泛函理论(DFT)的第一性原理平面波超软赝势(PWPP)方法，模拟计算未掺杂，Lu、F单掺杂及Lu-F共掺杂ZnO的几何结构、能带结构、态密度分布、光吸收谱和介电常数等性质。结果表明：掺杂后ZnO的晶格常数发生畸变，晶胞体积增大，禁带宽度不同程度地减小；在光学性质方面，F单掺杂较Lu单掺杂和Lu-F共掺杂时在可见光区的吸收系数和反射低，反映前者在可见光范围具有较高的透射率。

ZnO；第一性原理；共掺杂；电子结构；光学性质

近年来宽禁带的半导体固体电子学和光学器件方面引起了广泛关注，ZnO作为一种新型Ⅱ-Ⅶ族宽禁带(3.37 eV)半导体，因为其具有高达60 meV的激子束缚能和直接带隙等优良性质，在太阳电池、紫外光探测器、表面声波器件以及气体传感器方面有着广阔的应用前景[1−4]。但是本征ZnO的性质也存在缺陷，所以近来，人们开始通过掺杂来改善ZnO的性质。许多报道表明，稀土元素因为具有独特的最外层电子层结构而成为ZnO掺杂体系的研究热点。例如在ZnO中掺入稀土元素可以实现稀土离子的高效光致发光，实现1.54 μm波段的近红外发射，提高ZnO的气敏压敏特性[5]。在实验上，徐井华等[6]用凝胶溶胶法制备了不同浓度La掺杂的ZnO薄膜，紫外发光峰随着掺杂浓度的提高明显增强，并向短波方向移动。李泓霖等[7]采用平面波超软赝势法分析了Er和Gd掺杂对ZnO电子结构和光吸收的影响，发现稀土原子的4f轨道芯电子导致费米能级附近杂质能级的出现，介电虚部发生显著差异，掺杂体系的吸收系数提高。CHE等[8]研究了溶胶凝胶法制备的Eu掺杂ZnO薄膜，发现所有薄膜在可见光区的透射率均在80%以上，且随掺杂量的增加透射率降低；Eu3+掺杂在最大固溶度以下，未改变ZnO的带隙宽度;在理论计算方面，刘玮洁等[9]用Yb2+，Yb3+分别掺杂ZnO，结果发现与本征ZnO相比，这两种掺杂都增大了静态介电函数，吸收带边红移，并在0.91eV处出现了较强的吸收峰。吴玉喜等[10]研究了Y(La)替位Zn掺杂ZnO,发现了由杂质离子的d−d轨道跃迁引起的新的吸收峰，改变了介电常数，这为开发新的介电材料和折射材料提供了理论依据。

La系稀土掺杂ZnO的研究，不论是实验还是理论计算都已经有很多文献报道过，但是Lu元素掺杂ZnO的相关研究很少报道，而Lu-F共掺杂理论上可以改变薄膜中掺杂离子与ZnO基体间的电子和能量的传递方式，本文作者已经计算过Ga-F共掺杂ZnO并且证明F掺杂很大程度提高了ZnO的透射率，在此将进一步研究Lu-F对ZnO性质的影响。第一性原理可预测半导体掺杂后的相关性质[11−12]，在材料结构设计、分析计算等方面得到广泛的应用[10]。因此，本文作者利用基于密度泛函理论的第一性原理对Lu、F单掺杂以及Lu-F共掺杂的ZnO进行计算并对计算结果进行分析，以期为实验和实际应用提供相关理论基础。

1 计算模型和方法

1.1 计算模型

理想的ZnO是六方纤锌矿结构，所属空间群为63，对称性为6-4，其晶胞由O的六角堆积和Zn的六角密堆积在轴方向反向嵌套而成。晶格常数的实验值为==3.249 Å，=5.206 Å。O原子位于4个相邻Zn原子形成的四面体空隙中，即形成O-Zn4四面体，Zn原子的排列结构和O原子相似。选取2×2×2的ZnO超晶胞结构进行计算，总共32个原子，分别用F原子替代O原子，Lu原子替代Zn原子，建立了Zn15LuO15、Zn16FO15和Zn15LuFO15的超晶胞，如图1所示，掺杂后Lu和F的掺杂浓度为3.25%(摩尔分数)，比较符合实际掺杂。

图1 Lu-F共掺杂ZnO结构模型图

1.2 计算方法

在对Lu-F掺杂ZnO体系计算时采用了MS7.0软件中的CASTEP软件包(Cambridge Sequential Total Energy Package)[13]。计算中首先对ZnO超晶胞结构进行优化，优化中电子间相互作用的交换关联能由广义梯度近似下的PBE进行描述[14]。所有计算均在倒易空间中进行。具体相关参数设置如下：能量收敛标准为1×10−5eV/atom，平面截止能为350eV，第一布里渊区按3×3×1分格，快速傅里叶变换网格40×40×40，最大位移为0.001 Å，原子间相互作用力的收敛标准0.3 eV/nm，参与计算的价电子Zn：3d104s2，F：2s22p4，Lu：4f145p65d16s2，O：2s22p4。

2 计算结果与分析

2.1 几何优化结果

表1所列为不同掺杂情况下ZnO的晶格常数和超晶胞体积。与未掺杂的ZnO相比各个掺杂体系的ZnO晶格常数和体积都有不同程度的变化。其中本征ZnO的计算值与实验值和其他理论计算值接近[15]。F−(0.133 nm)的离子半径比O2−(0.14 nm)的离子半径小，因此F替位O原子后F—Zn键长(0.219 nm)均比原来的O—Zn键长(0.200 nm)增大，导致F掺杂后晶胞发生畸变，体积增大。对于Lu掺杂的ZnO，Lu的半径大于Zn的原子半径，并且Lu—O的平均键长大于之前的Zn—O键长，二者的共同作用导致晶格常数和晶胞体积增大。而Lu-F共掺杂的ZnO同样是由于上述原因而导致晶格膨胀，晶胞体积增大。

表1 掺杂前后ZnO几何结构参数

2.2 能带结构

图2所示为掺杂前后ZnO沿第一布里渊区高对称方向的能带结构图，能带图2中始终将电子能够填充的最高能级作为能量零点。从图2(a)可以看出，本征ZnO导带底和价带顶位于布里渊区同一点即点，为直接带隙半导体，禁带宽度为0.719 eV，这与何静芳等[16]计算的结果接近。但比实验值低很多，这是由于GGA近似带来的影响。但是作为一种有效的近似方法，计算结果的相对值是非常准确的，不影响对计算结果的定性分析。从图2(b)可以看出F掺杂后导带下移2.405 eV，价带下移2.234 eV，导致禁带宽度减小，并且导带和价带的能级变密，费米能级进入导带，属于n型掺杂。图2(c)所示为Lu掺杂后的ZnO的能带图，由图2(c)可以看出掺杂后的变化基本与F掺杂后的变化类似，使得禁带宽度进一步减小，减小为0.633 eV。Lu-F共掺杂后，相对于其他体系，禁带宽度变得最小0.363 eV，禁带宽度的减小，可以使得电子具有较小的能量就可以发生跃迁。并且导带和价带的能级变的更加密集，这是因为Lu-F共掺杂具有协同效应，相对于单掺杂具有更多的价态。

2.3 态密度

图3所示为ZnO掺杂前后各个体系的态密度图。由图3(a)中可以看出本征的ZnO的导带主要由Zn的4s轨道电子提供，在−6~0 eV范围内的价带由Zn3d和O2p轨道电子杂化而成，在−18~−16 eV的范围内存在孤立的态密度峰，主要由O2s轨道提供。掺杂后总的态密度整体向低能端移动，并且3个总态密度峰均展宽，局域性减弱。F单掺杂后，F的2p轨道、Zn3d轨道与O2p轨道共同构成−9~0 eV的价带，对导带基本没有贡献，而F2s轨道只对低能端的价带有贡献，这对掺杂材料的整体性能影响很小，可以忽略不计。Lu单掺杂后，可以看出总的态密度在−5~−4 eV出现了一个尖峰，观察Lu的分态密度图可知，这个态密度尖峰是由Lu的4f轨道贡献，并且Lu5d轨道对导带也有较大的贡献。Lu-F共掺杂后，总的态密度图相对于未掺杂和其他掺杂体系明显的向低能端移动(4 eV)，费米能级进入导带。

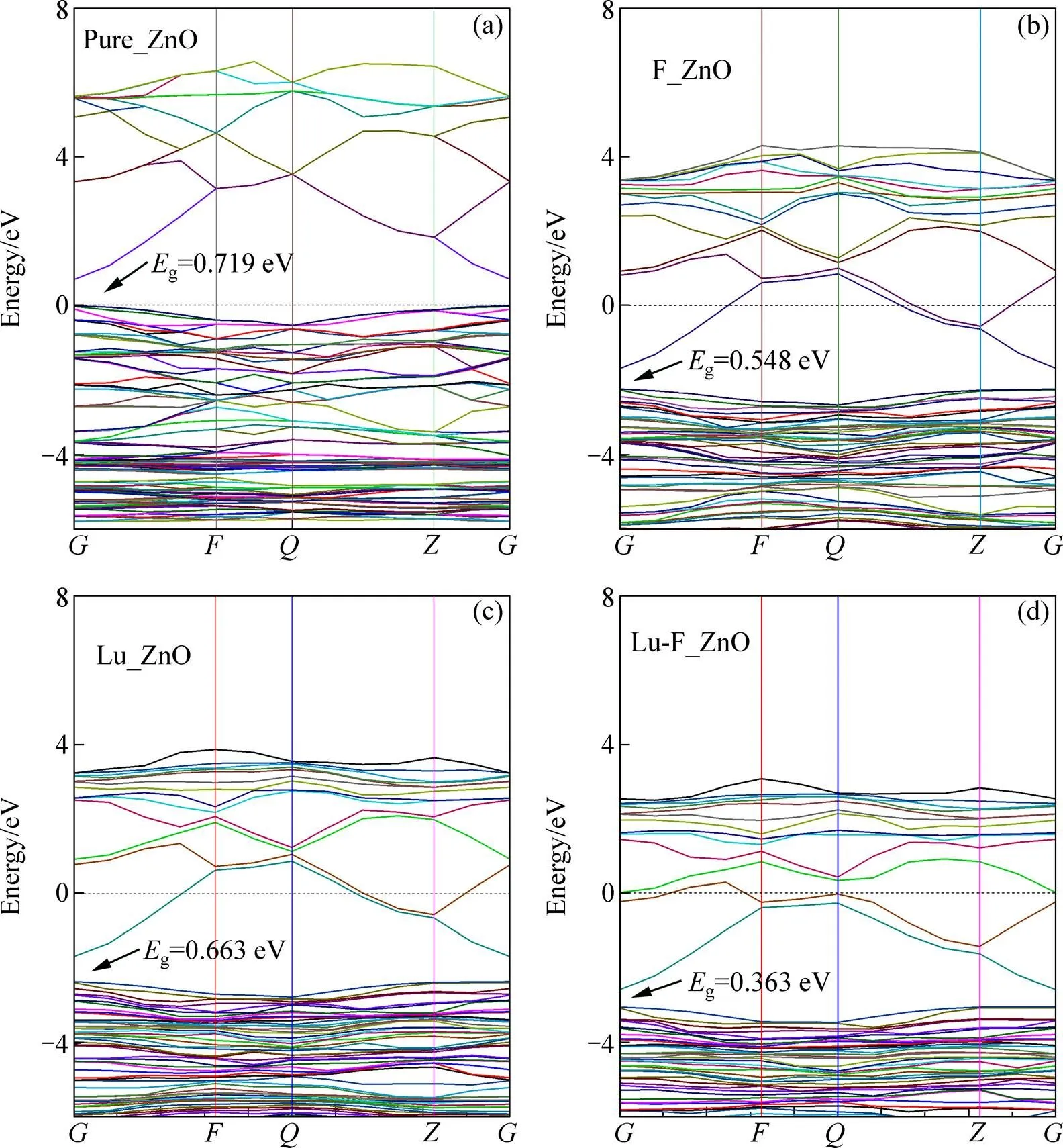
图2 未掺杂和掺杂后的ZnO晶体能带结构图

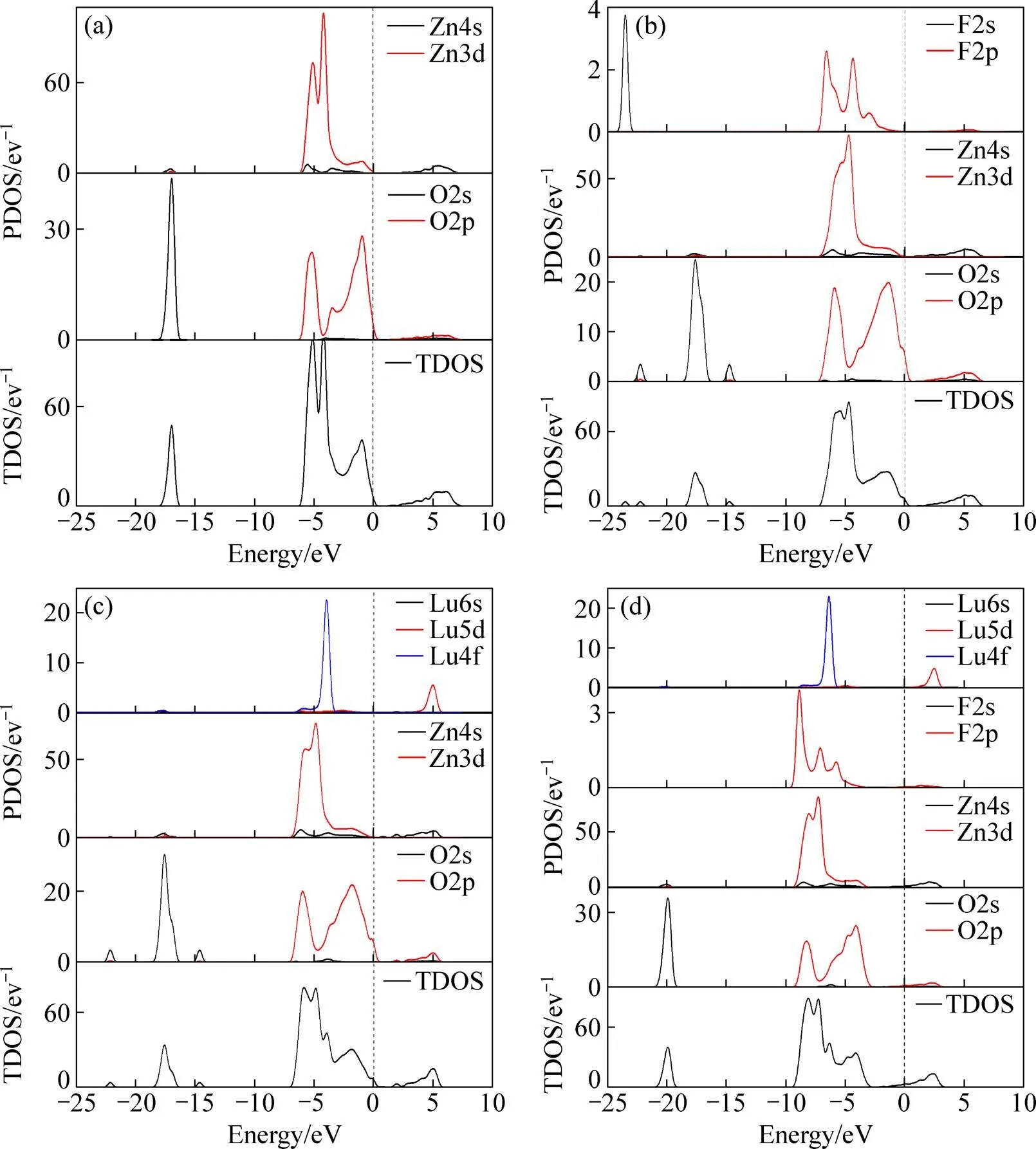
图3 未掺杂和掺杂后的ZnO电子总态密度(DOS)和分态密度(PDOS)图

2.4 光学性质

在第一性原理研究中通常用复介电函数来描述固体的宏观光学响应函数，复介电函数()的表达式为

()=1()+2() (1)

式中：为频率；1()和2()分别为介电函数的实部和虚部。介电函数的虚部2()是与光学吸收直接相关联的，可以根据电子跃迁的选择定则，由占据态和未占据态的电子波函数之间的矩阵元计算得到。实部1()可以利用Kramaer-Kronig关系由虚部2()计算得到。由1()和2()可以计算出其他的光学参数[17]。

图4(a)所示为掺杂前后ZnO的介电函数实部随光子能量变化图。从图4(a)中可以看出，本征的ZnO的实部主要有3个峰值，分别出现在1.7 eV，6.4 eV和10.2 eV，这与其他的计算结果较为接近。结合本征ZnO的能带图和态密度图可知，1.7 eV左右的峰值主要由O2p和Zn4s轨道之间的电子跃迁形成，6.4 eV左右的峰值主要由Zn3d和O的2p轨道之间的电子跃迁形成，10.2 eV左右的峰值主要由O2s和Zn3d轨道之间的电子跃迁形成。掺杂后对介电函数的影响主要集中在低能端，F单掺杂后第一个峰消失，这是因为F掺杂后能带下移，在1.7 eV左右不存在O2p与Zn4s轨道之间的电子跃迁引起的，并且在0~4 eV范围内曲线向高能端移动。Lu单掺杂后，同样第一个峰也消失，这也是由上述原因产生的，但是在6.4 eV附近形成一个高于本征ZnO的峰值，这是因为Lu的4f轨道电子位于4.8 eV附近，可以在不同的能级之间产生跃迁，在态密度图中也可以看出在4.4 eV附近Lu4f轨道对态密度有较大的贡献，并且在6.4 eV左右还有Zn3d轨道和O2p轨道电子的跃迁，所以形成一个比较大的峰值。Lu-F共掺杂后在高能端的变化趋势与Lu单掺杂类似，但是在低能端0.5 eV附近形成一个峰值，并且还有一个较小的波谷，这是Lu-F共掺杂产生的 影响。

图4(b)所示是掺杂前后ZnO的吸收系数图，这部分计算为了使其与实验值相近，采用了剪刀修正法，修正值取2.6 eV(禁带宽度的实验值与计算值之差)。从图中可以看出，本征的ZnO吸收带边位于2.9 eV，接近于带隙的实验值3.37 eV，并且有3个主峰值。分别位于4.5 eV，10.2 eV和13.8 eV。这与关丽等[18]计算结果较为接近。F和Lu单掺杂后，在低能端吸收带边均向高能端方向移动，不同的是Lu单掺杂后在12 eV左右产生一个较高的峰值，这说明Lu掺杂后增大了ZnO在紫外光范围内的吸收系数。而Lu-F共掺杂后在高能端的变化与Lu单掺杂变化类似，在低能端表现为：吸收带边的红移，增加了对可见光的吸收范围。图4(c)所示为ZnO掺杂前后反射率变化情况，在可见光范围内，纯净的ZnO的反射峰位于14.8 eV左右，掺杂导致反射峰发生不同程度的向低能方向移动，其中共掺杂时反射峰移动最为明显。Lu-F共掺杂和Lu掺杂时反射峰升高明显，而F单掺杂时反射峰变化很小，说明前者紫外光透射率增加。能量损失可以反映电子在通过均匀的电介质时能量的损失情况。图4(d)所示为ZnO掺杂前后能量损失，纯净的ZnO能量损失峰值位于15 eV左右，这与实验值18.8 eV十分接近[19]。掺杂后，能量损失出现不同程度的红移，其中Lu-F共掺杂时红移最明显。值得注意的是，能量损失峰值与反射谱线的迅速下降直接对应。

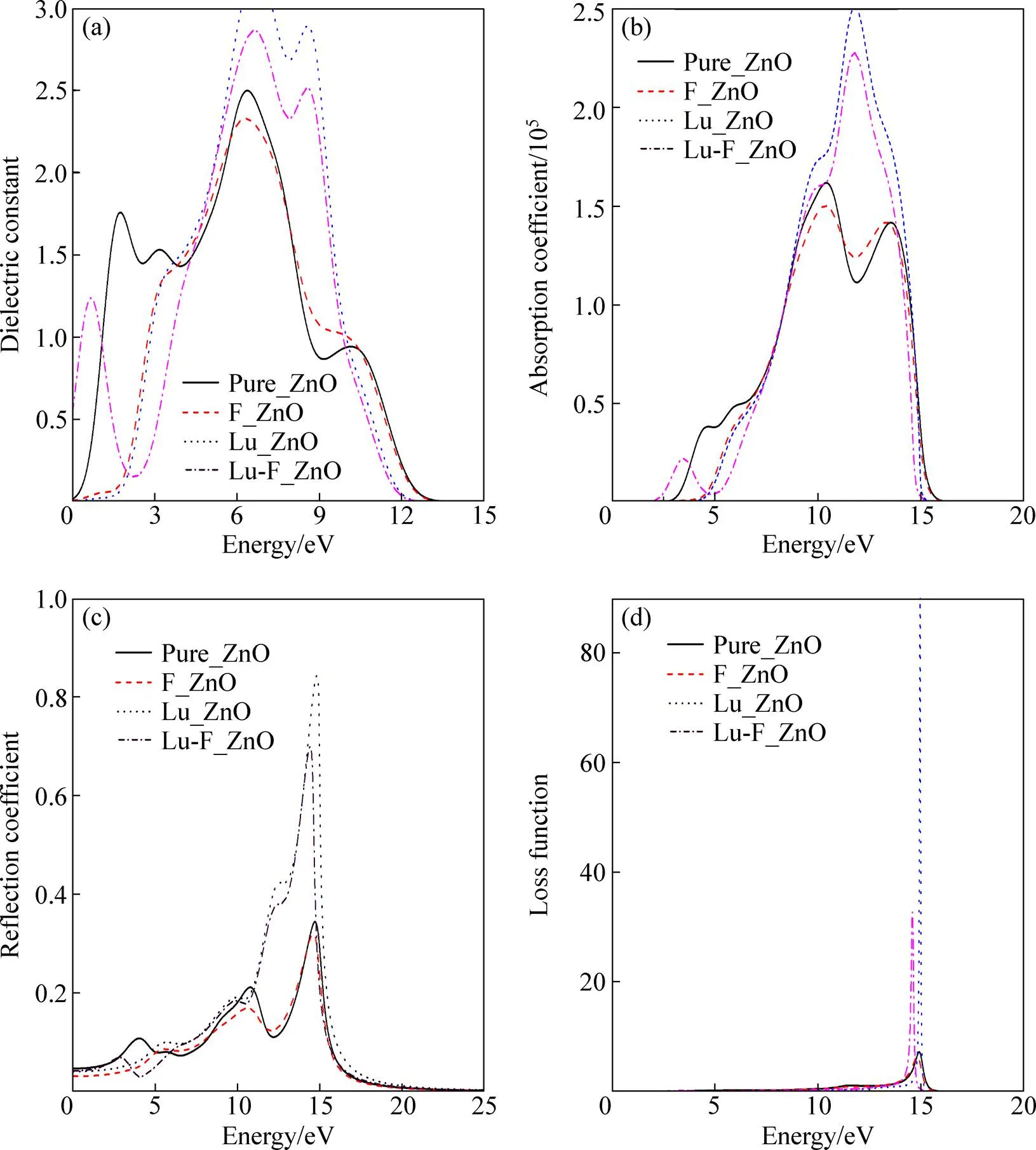
图4 未掺杂和掺杂后的ZnO光学图谱

3 结论

1) 掺杂导致晶格畸变，体积膨胀；掺杂后与掺杂前的ZnO相比禁带宽度减小，导带和价带的能级变密，有利于电子在带隙间的跃迁。

2) 掺杂后ZnO的光学性质得到改善，其中Lu掺杂后由于稀土元素特殊的外层电子结构，增大了电子的跃迁几率，并且增强了紫外区域的吸收系数和可见光的吸收范围。

致谢：感谢河北大学刘保亭教授为本文提供CASTEP软件并参与计算结果的讨论。

REFERENCES

[1] LEE K E, WANG M, KIM E J, HAHN S H. Structural, electrical and optical properties of sol–gel AZO thin films[J]. Current Applied Physics, 2009, 9(3): 683−687.

[2] HASABELDAIM E, NTWAEABORWA O M, KROON R E, SWART H C. Surface analysis and cathodoluminescence degradation of undoped ZnO and ZnO: Zn phosphors[J]. Journal of Vacuum Science & Technology B, 2016, 34(4): 041221(1−8).

[3] LANG Ji-hui, HAN Qiang, YANG Jing-hai, LI Chang-sheng, LI Xue, YANF Li-li, ZHANG Yong-jun, GAO Ming, WANG Dan-dan, CAO Jian. Fabrication and optical properties of Ce-doped ZnO nanorods[J]. Journal of Applied Physics, 2010, 107(7): 074302(1−4).

[4] GORAI P, ERTEKIN E, SEEBAUER E G. Surface-assisted defect engineering of point defects in ZnO[J]. Applied Physics Letters, 2016, 108(24): 241603(1−5).

[5] 李瑛娟, 陈清明, 马 吉. 稀土掺杂ZnO薄膜的研究进展[J]. 材料导报A, 2012, 26(8): 32−37. LI Ying-juan, CHEN Qing-ming, MA Ji. Research progress of rare earth doped ZnO thin films[J]. Materials Review, 2012, 26(8): 32−37.

[6] 徐井华, 刘有成. 不同浓度La掺杂ZnO薄膜光学特性的研究[J]. 通化师范学院报, 2010, 31(4): 24−25. XU Jing-hua, LIU You-cheng. The study of La doped ZnO thin films optical properties[J]. Journal of Tonghua Normal University, 2010, 31(4): 24−25.

[7] 李泓霖, 张 仲, 吕英波, 黄金昭, 张 英, 刘如喜. 第一性原理研究稀土掺杂ZnO结构的光电性质[J]. 物理学报, 2013, 62(4): 047101(1−6). LI Hong-lin, ZHANG Zhong, LÜ Ying-bo, HUANG Jin-zhao, ZHANG Ying, LIU Ru-xi. First principles study on the electronic and optional properties of ZnO doped with rare earth[J]. Acta Physica Sinica, 2013, 62(4): 047101(1−6).

[8] CHE P, MENG J, REN L R, LIN G. Fabrication and magnetic properties of highly oriented ZnO:Eu films by sol-gel process[J]. Journal of Rare Earths, 2006, 24(1): 298−301.

[9] 刘玮洁, 孙正昊, 黄宇欣, 冷 静. 不同价态稀土元素Yb掺杂ZnO的电子结构和光学性质[J]. 物理学报, 2013, 62(12): 127101(1−7). LIU Wei-jie, SUN Zeng-hao, HUANG Yu-xin, LENG Jing. Electronic structures and optical properties of rare earth element(Yb) with different valences doped in ZnO[J]. Acta Physica Sinica, 2013, 62(12): 127101(1−7).

[10] 吴玉喜, 胡智向, 顾书林, 渠立成, 李 腾, 张 昊. 稀土元素(Y, La)掺杂ZnO的电子结构和光学性质[J]. 物理学报, 2011, 60(1): 017101(1−7). WU Yu-xi, HU Zhi-xiang, GU Shu-lin, QU Li-cheng, LI Teng, ZHANG Hao. Electronic structures and optical properties of rare earth element (Y, La) doped in ZnO[J]. Acta Physica Sinica, 2011, 60(1): 017101(1−7).

[11] 段国玉, 宋思超, 魏昌东,王松有, 贾 瑜. HfTi1−xO2电子结构与光学性质的第一性原理研究[J]. 红外与毫米波学报, 2010, 29(4): 264−267. DUAN Guo-yu, SONG Si-chao, WEI Chang-dong, WANG Song-you, JIA Yu. Electronic structures and optical properties of HfTi1−xO2calculated from first peinciples[J]. J Infrared Millim Waves, 2010, 29(4): 264−267.

[12] 张会媛, 邢怀中, 张 蕾. Ga/N共掺杂对InSb电子结构的影响[J]. 红外与毫米波学报, 2012, 31(3): 231−234. ZHANG Hui-yuan, XING Huai-zhong, ZHANG Lei. The effect of Ga/N Co-doping on electronic structure og InSb[J]. J Infrared Millim Waves, 2012, 31(3): 231−234.

[13] CLARK S J, SEGALL M D, PICKARD C J, HASNIP P J, PROBERT M J, REFSON K, PAYNE M C. First principles methods using CASTEP[J]. Z Kristallogr, 2005, 220(5/6): 567−570.

[14] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77: 3865−3868.

[15] 陈 琨, 范广涵, 章 勇. Mn掺杂ZnO光学特性的第一性原理计算[J]. 物理学报, 2008, 57(2): 1054−1060. CHEN Kun, FAN Guang-han, ZHANG Yong. First principles study of optical properties of wurtzite ZnO with Mn-doping[J]. Acta Physica Sinica, 2008, 57(2): 1054−1060.

[16] 何静芳, 郑树凯, 周鹏力, 史茹倩, 闫小兵. Cu-Co共掺杂ZnO光电性质的第一性原理计算[J]. 物理学报, 2014, 63(4): 46301(1−9). HE Jing-fang, ZHENG Shu-kai, ZHOU Peng-li, SHI Qian-ru, YAN Xiao-bing. First-principles calculations on the electronic and optical properties of ZnO codoped with Cu-Co[J]. Acta Physica Sinica, 2014, 63(4): 46301(1−9).

[17] 沈学础. 半导体光谱和光学性质[M]. 2版. 北京: 科学出版社, 2002: 23−24. SHEN Xue-chu. Spectroscopy and optical properties of semiconductors[M]. 2nd ed. Beijing: Science Press, 2002, 23−24.

[18] 关 丽, 李 强, 赵庆勋, 郭建新, 周 阳, 金利涛, 耿 波, 刘保亭. Al和Ni共掺杂ZnO光学性质的第一性原理研究[J]. 物理学报, 2009, 58(8): 5624−5630. GUAN Li, LI Qiang, ZHAO Qing-xun, GUO Jian-xin, ZHOU Yang, JIN Li-tao, GENG Bo, LIU Bao-ting. First-principles study of the optical properties of ZnO doped with Al, Ni[J]. Acta Physica Sinica, 2009, 58(8): 5624−5630.

[19] LU J G, FUJITA S, KAWAHARAMURA T, NISHINAKA H, KAMADA Y, OHSHIMA T, YE Z Z, ZENG Y J, ZHANG Y Z, ZHU L P, HE H P, ZHAO B H. Carrier concentration dependence of band gap shift in n-type ZnO: Al films[J]. Journal of Applied Physics, 2007, 101(8): 83705(1−7).

(编辑 王 超)

First-principles calculations on electronic and optical properties of ZnO codoped with Lu-F

ZHANG Ming-ju1,2, LI Wen-ming1, 2, ZHENG Shu-kai1, 2

(1. College of Electronic and Informational Engineering, Hebei University, Baoding 071002, China;2. Research Center for Computational Materials and Device Simulations,Hebei University, Baoding 071002, China)

The geometry and band structures, density of states, light absorption spectra and dielectric constants of pure ZnO, Lu, F single doped, and Lu-F co-doped ZnO were calculated using the plane-wave ultra-oft pseudo-potential (PWPP) method based on density functional theory (DFT). The calculated results indicate that the lattice constants of doped ZnO are distorted and the volumes increase. The band gaps of the doped ZnO are reduced with different degrees. In terms of the optical properties, the absorption coefficient and reflectivity of F-ZnO are smaller than those of Lu-ZnO and (Lu-F)-ZnO, which indicate a higher transmittance of the F doped ZnO in the visible light range.

ZnO; first principle; codoped; electronic structure; optical property

Project(ZD2017008) supported by Key Program of Science and Technology Research of Colleges and Universities in Hebei Province, China

2016-04-21; Accepted date: 2016-10-20

ZHENG Shu-kai; Tel: +86-15932188935; E-mail: zhshk@126.com

10.19476/j.ysxb.1004.0609.2017.05.012

1004-0609(2017)-05-0960-07

0471；0472

A

河北省高等学校科学技术研究重点项目(ZD2017008)

2016-04-21；

2016-10-20

郑树凯，副教授，博士；电话：15932188935；E-mail：zhshk@126.com