例说函数的教学设计与策略

⌾高晓伦

例说函数的教学设计与策略

⌾高晓伦

本文通过一堂函数复习课来优化教学设计以及在教学过程中采取的一些教学策略来说明教学不拘泥于教材而创新设计课堂教学.

教学设计；教学策略

一、课程设计的原因

函数的概念从数学史的角度上说有过两种观点：从传统的变化过程观点发展到近代的对应关系(以集合论为基础)的观点，这种变化能够解决传统观点的一些不足。但这正是学生理解上的障碍，但是这两种观点在理解某些问题时又各有长度，因此在教学过程中要体现两种观点的优缺点，但主要目的还是让学生理解近代函数观点为主。

二、教学引入及问题的提出

板书：一个变化过程有两个变量x,y，其中一个变量y随着另一个变量x的变化而变化，我们就把y叫做x的函数。

师：上面我们给的两个学过的函数是不是满足这个概念？(可以引导一同完成)

生：满足。

师：问题1：看下面这个变化过程是不是函数呢？寄信时，邮资会随信件的重量变化而变化，那么邮资是不是信件质量的函数呢？如果是怎么表示这个函数呢，如果不是说明理由。(见旧人教版高中数学教材)

问题2:若y2=x，y是不是x函数呢？答案明确的说不是，但用初中知识能解决吗?

三、近低函数概念的教学的引入与深化的整合

1.重新重视“对应”这个名词，它是理解近低函数定义的基础。

教学过程：

板书：大千世界对应关系无处不在！

学生：气氛反应活跃，有的笑：老师也玩深沉！

师：请玩手机的那个同学把手机交到讲台上来。

学生：气氛一下紧张，四个找寻是哪个学生！？

等了一会儿，师：为什么没有同学交手机上来呢？因为你们都会自然想到不是我呀，我没玩手机呀!你们是不是自然就发生了一个对应呢，去对应某个对象。

生：一下恍然大悟，有的面带会意的微笑，气氛一下活跃起来了。

板书：每一种对应关系都有适用范围！

师：明天请你们把家长请到学校来，你们知道请谁吧？有没有调皮蛋乱请呀！更甚而至于去找个其它什么如猴子的来吧(玩笑，玩笑，没有要骂人的意思)。请问，找家长适用于范围是什么呢？得应该对人说，对吧。(这对后边能力提升部分的函数定义域的理解是有帮助的)。

生：明白。

2.映射是一种特殊的对应关系，它将对函数作出明确的数学定义。

教学过程：

板书：映射是一种特殊的对应关系。

特殊在1、是两个集合上的对应关系

2、有方向。

3、只考察其中一集合的元素满足的两个条件。

以集合A到B的映射的符号表示为f:A→B为例，每一个映射都有三要素，原象集A，对应关系f，象集B。要求A中每个元素通过对应关系f在B中都有且只唯一的元素与之对应即可。

思考1、所有的对应关系都是映射吗？

2、能举出几个是映射和不是映射的对应关系吗？

3、映射都是对应关系吗？

在学生能解决以上问题后就为学习以集合论为基础的近代函数的定义了。

3.进一步设计近代函数教学过程与策略。

板书：

环节一：

问题1、阅读教材函数的定义，能精简为板书上的内容吗？

2、特殊在什么地方？

例：下面几个对应关系y是不是x的函数？又是不是从x的集合到y的集合的映射呢？1、

x1234y3312

2、y=2x2+x+3； 3、y2=x； 4、前面的邮资问题。

环节二(函数符号的理解)：

观点一：y=f(x)⟺f:x→y；

例、 前面邮资问题看作f(邮件质量)=邮资行吗？那么f(5.7)=?

观点二：每种对应关系都有适用范围，对函数是不也有适用范围(定义或问题)呢？函数定义或的三种情况：法定、实定、给定。

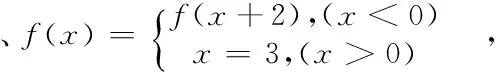
4.能力提高(每一种对应关系都有适用范围)：

例、f(x)的定义域为(2,4)，那么f(x+2)的定义域为多少？

例、f(x-2)的定义域为(2,4)，那么f(x+2)的定义域为多少？

四、总结反思

1.我们学到了什么：通过把函数建立在对应关系这个基础概念上，便于对函数的一些抽象的不好理解的地方便于简单明了化。在早期教材中有过类似的编排，我个人觉得这样处理能让抽象问题实际化，以便于操作，并且为今后的学习抽象的函数知识打下基础。

2.本教学设计针对对象：这个教学设计最好是在学生有一定的基础的时候复习课，作为新课要作实际调整，如分成两课时来完成，让学生有更多间讨论事先设计好的问题来加深即可。

3.与新课改不相矛盾：本教学设计也体现了以教师为主导和以学生为主体的教学理念，以师的导为重，师生互动与情感交流都能达到良好效果。

4.课型选择：我个人认为象这种抽象的理论章节以选师起引导的课型为好，让学生全程探究形式不可取。

旧人教版、新人教版、新苏教版高中数学教材

重庆市巴南区渝南田家炳中学 401346)