结构函数法计算镀层表面轮廓曲线分形维数的适应性研究

魏静，吴成宝,*，田巨，陈峥华，刘传生，龚煜，王舰，李璐瑶

（1.广州民航职业技术学院飞机维修工程学院，广东 广州 510470；2.华南理工大学机械与汽车工程学院，广东 广州 510640；3.广州白云国际机场地勤服务有限公司机务工程部，广东 广州 510470）

结构函数法计算镀层表面轮廓曲线分形维数的适应性研究

魏静1，吴成宝1,2,*，田巨1，陈峥华3，刘传生1，龚煜1，王舰1，李璐瑶1

（1.广州民航职业技术学院飞机维修工程学院，广东 广州 510470；2.华南理工大学机械与汽车工程学院，广东 广州 510640；3.广州白云国际机场地勤服务有限公司机务工程部，广东 广州 510470）

为验证结构函数法(SFM)计算镀层表面轮廓曲线分形维数的适应性，利用W−M分形函数生成了空间频率相关参数(λ)和特性参数(G)不同，但理论分形维数(D)均为1.5的标准表面轮廓曲线，并用SFM测算了它们的D。统计分析结果发现：λ一定时，SFM的计算相对误差为0.04% ～ 0.07%，平均相对误差仅为0.05%；G一定时，SFM的计算相对误差为0.27% ～ 1.01%，平均相对误差为0.62%。较低的相对误差表明SFM在测算不同特性曲线的D时具有极强的适应性。

镀层；轮廓曲线；分形维数；结构函数法；适应性；相对误差

Abstract:The standard surface profile curves with different values of characteristic parameter (G) and spatial frequency parameter (λ) but the same fractal dimension (D = 1.5) were generated by the W-M fractal function, and their D values were calculated by the structure function method (SFM).The statistical analysis of calculated results indicated that the relative error of SFM is in a range of 0.04%-0.07% with an average value of 0.05% when the λ is constant, and the relative error of SFM ranges from 0.27% to 1.01% and is 0.62% averagely when the G is constant.The small relative errors show that the SFM is highly adaptable to calculate the D values of the curves with different characteristics.

Keywords:coating; profile curve; fractal dimension; structure function method; adaptability; relative error

First-author’s address:School of Aircraft Maintenance Engineering, Guangzhou Civil Aviation College, Guangzhou 510470, China

镀层表面具有分形结构，可以用分形维数来定量表征[1-5]。笔者课题组的前期工作[6]评价了垂直界面法、尺码法、盒维数法、方差法、结构函数法(SFM)、协方差加权法、功率谱法和均方根法用于计算标准表面轮廓曲线的分形维数(D)时的准确性。从研究结果可以初步判断：在上述8种常用方法中，结构函数法最准确。但评价的对象是由具有相同的空间频率相关参数( )和特性参数(G)的标准分形函数生成的曲线，而真实的镀层表面形貌空间频率是随机的。因此，具有最高准确度的结构函数法是否适应于计算具有不同空间频率和不同特性参数值的曲线的分形维数还有待进一步验证。本文用W-M分形函数生成了理论分形维数为1.5，但具有不同特性参数和空间频率相关参数的标准分形曲线，分析了结构函数法的计算误差，验证了该方法的适应性。

1 结构函数法的简介

将轮廓曲线视为一个时间序列Z(x)，则具有分形特征的时间序列能使其采样数据的结构函数满足式(1)[7-8]：

则D与斜率α的转换关系如式(2)所示。

2 标准轮廓曲线的生成

2.1 W-M分形函数

W-M分形函数是由1875年发现的连续但处处不可微的函数演变而成。1980年，M.V.Berry详细讨论了W-M分形函数的数学性质，奠定了W-M分形函数广泛传播和适用的基础。后来，B.B.Mandelbrot、H.O.Peitgen等人提出了轮廓曲线具有统计自相似分形特征，可用W-M分形函数来刻画表征。1990年为了适合工程表面的应用，M.Majumdar和B.Bhushan提出了对原W-M分形函数的修正形式，简称M-B模型。其表达式如式(3)[9]所示。

式中， Z(x)为随机轮廓高度； 为轮廓的位置坐标；G为特征尺度系数，反映 Z(x)的幅值，它决定 Z(x)的尺寸；D为W-M分形曲线的分形维数，它描述函数 Z(x)在所有尺度上的不规则性，但不能确定 Z(x)的尺寸，即两个完全不同尺度上的分形曲线可以具有相同的分形维数；λn为轮廓的空间频率， 为大于1的常数，对于服从正态分布的随机轮廓， = 1.5可适用于高频密度及相位的随机性，由于粗糙度轮廓是非稳定的随机过程，轮廓结构的最低频率与粗糙度样本长度的关系为； nL是W-M分形函数的初始项，是整数； L1为粗糙度样本取样长度；n为样本取样长度上的取样个数，是整数。

2.2 W-M分形函数的MATLAB实现

由式(3)可知，W-M函数主要由D、G、、n所确定，同时要避开0λ=的点，另经大量计算发现n不可能取无穷大，也不需要取过大值，实际应用中一般为10 ～ 100， 则在[0.5, 0.8]区间内取值。

在Matlab中，D为1.5时的模拟程序如下(其他情况只需将程序中的D改成相应的分形维数值)：

subplot(2,2,1)

x=0.5:0.0001:0.8

c=0

for n=1:100

g=0.01,lambda=1.5, D=1.5

z=g.^ (D-1)* cos(2*pi*lambda.^n*x)/lambda.^ ((2-D)*n)

c=c+z

end

plot(x,c)

3 结果与分析

D为1.5，G分别为0.01、0.1、10和100时，W-M分形函数的模拟图如图1所示。

D为1.5， 分别为1.4、1.6、1.8和2.0时，W-M分形函数的模拟图如图2所示。

为验证结构函数法的适应性，考察了当 = 1.5时不同特征尺度系数(G值)条件下D为1.5的W-M曲线的实测值，其计算曲线见图3。用最小二乘法原理线性回归分析各数据点，结果见表1。

由图3可知，计算曲线呈线性相关。结合表1可以看出，结构函数法的D值计算曲线的相关系数都大于0.99，且波动仅为0.03%，这表明结构函数法具有十分显著的稳定性。此外，又选择了在G= 1，分别为1.4、1.6、1.7、1.8和2.0的条件下，理论D值为1.5时，分析结构函数法的准确性。其计算曲线如图4所示。用最小二乘法原理线性回归分析各数据点后的结果见表2。

图1 不同G值的W−M分形曲线Figure 1 W-M fractal curves having different G values

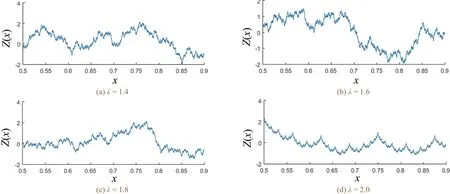
图2 不同λ值的W−M分形曲线Figure 2 W-M fractal curves having different λ values

图3 不同G值条件下W−M分形曲线的D值计算曲线(λ = 1.5)Figure 3 Plots for calculating the D values of the W-M fractal curves with different G values (λ = 1.5)

表1 不同G值条件下W−M分形曲线的实测D值(λ = 1.5)Table 1 Calculated D values of the W-M fractal curves with different G values (λ = 1.5)

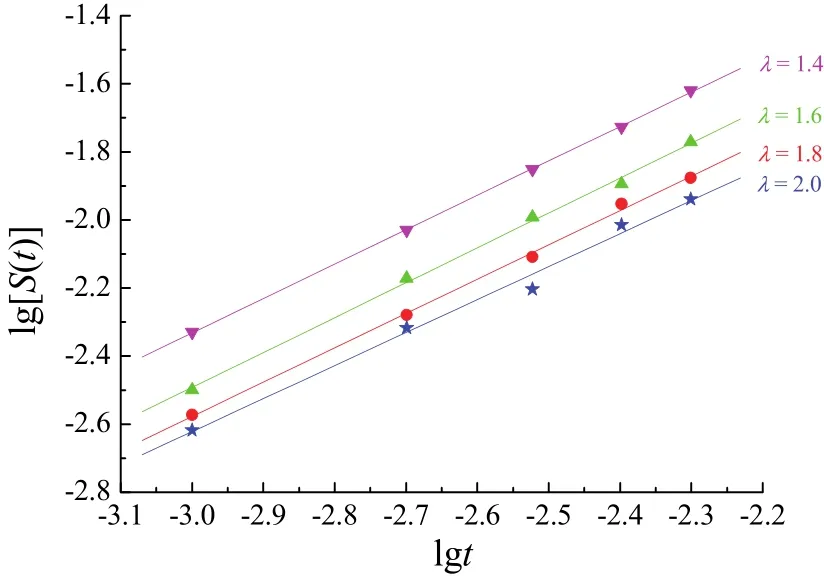
图4 不同λ值条件下W−M分形曲线的D值计算曲线(G = 1)Figure 4 Plots for calculating the D values of the W-M fractal curve with different λ values (G = 1)

表2 不同λ值条件下W−M分形曲线的实测D值(G = 1)Table 2 Calculated D values of the W-M fractal curves with different λ values (G = 1)

分析图4及表2不难发现，不同 值条件下，用结构函数法计算的D值的相对误差和误差波动都较小，平均误差仅为0.62%。这进一步说明结构函数法具有良好的适用性。

4 结论

结构函数法在计算具有不同空间频率相关参数和特性参数的标准表面轮廓曲线时，其相对误差分别介于0.04% ～ 0.07%与0.27% ～ 1.01%，平均相对误差分别为0.05%和0.62%。较低的相对误差表明结构函数法适用于测算不同特性曲线的分形维数。

[1]徐金来, 吴成宝, 刘钧泉.镀层表面形貌的分形维数定量表征[J].电镀与涂饰, 2009, 28 (5): 31-34.

[2]汪笑鹤, 徐滨士, 胡振峰, 等.n-Al2O3/Ni-Co纳米复合电刷镀层表面形貌的分形维数研究[J].电镀与涂饰, 2010, 29 (11): 33-36.

[3]郑金玲, 胡小芳. 镍−二氧化硅纳米复合镀层表面分形维数与显微硬度的关系[J].电镀与涂饰, 2011, 30 (9): 8-11.

[4]翁星星, 朱贤博.化学镀非晶镍−磷合金分形分析[J].电镀与涂饰, 2012, 31 (11): 28-31.

[5]王洪涛, 李艳, 朱华.具有分形特征的织构表面的润滑减摩性能研究[J].表面技术, 2016, 45 (9): 182-187.

[6]吴成宝, 田巨, 刘传生, 等.镀层表面轮廓曲线分形维数计算方法的评价[J].电镀与涂饰, 2017, 36 (8): 403-408.

[7]ZHONG L, ZENG F, XU G X.Comparison of fractal dimension calculation methods for channel bed profiles [J].Procedia Engineering, 2012, 28: 252-257.

[8]YUAN C Q, LI J, YAN X P, et al.The use of the fractal description to characterize engineering surfaces and wear particles [J].Wear, 2003, 255 (1/2/3/4/5/6):315-326.

[9]MAJUMDAR A, BHUSHAN B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J].Journal of Tribology, 1990, 112 (2):205-216.

[ 编辑：温靖邦 ]

《电镀与涂饰》学友录上线公告

欢迎加入《电镀与涂饰》学友录，本通讯录会免费赠阅《电镀与涂饰》杂志，请填写完整信息。

学友录内可免费发布招聘求职、供应采购等信息，资源共享，合作共赢！

Study on adaptability of structure function method for calculating the fractal dimension of surface profile curve of coating

WEI Jing, WU Cheng-bao*, TIAN Ju, CHEN Zheng-hua, LIU Chuan-sheng, GONG Yu, WANG Jian, LI Lu-yao

TQ153

B

1004 - 227X (2017) 17 - 0911 - 04

2017-07-02

2017-08-29

中国民用航空局2015年民航科技创新引导资金；广东省二类品牌专业建设项目；2017年广州民航职业技术学院校级科研项目。

魏静（1975-），女，四川成都人，硕士，副教授，主要从事民用飞机结构的研究。

吴成宝，副教授，(E-mail) wuchengbao@126.com。

10.19289/j.1004-227x.2017.17.002