不同湍流模式下钱塘江涌潮水流三维模拟

汪求顺，潘存鸿

(1. 浙江省水利河口研究院，浙江 杭州 310020; 2. 浙江省海洋规划设计研究院，浙江 杭州 310020; 3. 浙江省河口海岸重点实验室，浙江 杭州 310016)

不同湍流模式下钱塘江涌潮水流三维模拟

汪求顺1, 2, 3，潘存鸿1, 2, 3

(1. 浙江省水利河口研究院，浙江 杭州 310020; 2. 浙江省海洋规划设计研究院，浙江 杭州 310020; 3. 浙江省河口海岸重点实验室，浙江 杭州 310016)

钱塘江涌潮具有动力作用强和流速变化快等特点。涌潮水流紊动复杂，流速的垂向分布和紊动强度息息相关。通过涌潮水流实测资料的分析可以发现，涌潮作用下流速垂向分布在底部和上层存在差异。为研究涌潮作用下流速垂向分布的特征，应用基于非结构网格下有限体积法模型FVCOM对钱塘江涌潮河段水流运动进行三维数值模拟。考虑到涌潮紊动作用复杂且对流速的垂向分布起着重要影响，采用不同的湍流模式对涌潮传播过程中水流的运动特征开展研究。通过与涌潮河段实测资料的验证，复演涌潮到达前后水流运动特征，给出涌潮水流湍动能的变化过程。研究成果有助于深入认识涌潮水流紊动特征和流速的分布规律，为涌潮作用下物质输运的研究提供基础。

涌潮；三维模拟；湍动能；钱塘江河口；FVCOM

Abstract: The tidal bore in the Qiantang estuary has the characteristics of intense hydrodynamics and rapid-variation velocity. The turbulence of tidal bores is complicated, and turbulence intensity is closely relevant to the vertical distribution of velocity. It is found that the distribution of the velocity along the water depth is different at the bottom and the top layers under the tidal bore by the analysis of the field data. This study is to simulate the three-dimensional feature of the tidal bore in the Qiantang estuary based on the unstructured grids finite-volume method FVCOM model so as to investigate the distribution of velocity along the water depth. As the turbulence of the tidal bore is complicated and it plays an important role in the distribution of velocity, the tidal flows are studied during the propagation of tidal bores by different turbulence models. The movement of the flow is reproduced before and after the arrival of tidal bores by the calibration with the measured data, the time-varying process of turbulent kinetic energy is exhibited. The present results are helpful to deepen the understanding of turbulence characteristics and the distribution of velocity, and it will provide a basis for the study of mass transport.

Keywords: tidal bore; 3D simulation; turbulent kinetic energy; Qiantang estuary; FVCOM

目前，对于涌潮作用下二维水流运动的数值研究成果较多。潘存鸿等[1]通过守恒型浅水方程采用间断捕捉方法对钱塘江河口涌潮的平面运动特征进行了模拟。在涌潮水流现场实测数据的分析中可以发现，涌潮到达前后流速不仅在平面上存在突变，而且水深方向的流速在底部和上层存在差异。涌潮水流具有明显的时空梯度分布特征。为完整地反映涌潮水流的结构，需通过三维模型来复演水流的运动特征。李绍武等[2]通过建立三维潮流数学模型研究概化河道中涌潮水流运动。王灿星等[3]采用FLUENT软件对涌潮影响下的钱塘江三维水流结构进行了模拟。Liu等[4]基于无网格光滑粒子方法对涌潮的三维流场进行了模拟。谢东风等[5]基于FVCOM模型对钱塘江河口涌潮的三维运动进行了模拟，并指出底部糙率对流速垂向分布的准确模拟起着主要作用。陈永平等[6]在潮流模拟过程中选取不同涡黏系数类型研究三维水流的结构，结果表明垂向涡黏系数对水平流速的垂向分布起着重要作用。可以得出，涌潮作用下水流垂向分布不仅和底部糙率有关，还与湍流垂向紊动有着紧密联系。已有的涌潮作用下水流平面运动的数值研究表明，钱塘江河床糙率偏小[1]。当前对钱塘江河口涌潮作用下水流紊动特征的研究成果很少，对其进行深入研究有助于探讨水流的垂向分布机理。

涌潮在传播过程中会产生强烈的湍流紊动，国外学者通过物理模型试验、大涡模拟技术对涌潮作用下湍流过程进行了研究[7-9]。Xie和Pan[10]通过盐官站点涌潮水流的实测数据，对涌潮作用下水流的湍流紊动进行了初步研究，给出了雷诺应力的大小。湍流紊动和水流垂向分布有着紧密的联系。湍流紊动会引起水体湍动能的变化，进而影响水流的结构分布。熊伟等[11]在水动力方程中结合不同湍流模型研究了浅滩海域风暴作用下潮流的垂向结构。对于钱塘江涌潮河段，在强涌潮作用下，湍流紊动过程复杂，这对水体的对流扩散起着重要影响。为说明涌潮作用下水流在垂向上的分布差异，对涌潮水流紊动中湍动能的定量分析有助于认识涌潮水流的流速分布机理。

现有的研究准确地模拟了涌潮的平面运动特征，对钱塘江涌潮的形态进行了很好地复演，但反映涌潮水流垂向分布特征的数值研究很少。为准确地复演涌潮水流的垂向分布，应用基于非结构网格下有限体积法的开源模型FVCOM，通过结合不同的湍流模式，对钱塘江涌潮达到前后流速的分布进行研究，给出涌潮初始段和强涌潮段湍动能的变化过程。

1 三维数学模型

1.1控制方程

控制方程采用FVCOM模型中经雷诺时均的三维σ坐标下Navier-Stokes方程。为提高三维模型在实际河口区域的计算效率，考虑到垂向采用静压假定的三维模型在模拟涌潮时具有很好的精度[12]，因此垂向动量方程采用静压假定。

式中：t为时间；x，y和σ分别为水平和垂向坐标；ζ为水面的高度；u，v，w分别为x，y，σ方向流速；D为总水深；H为静水深；f为科氏常数；g为重力加速度；Am为水平紊动黏性系数；Km为垂向涡黏系数。考虑到水平紊动系数对流速分布的影响小[6]，采用Smagorinsky方程进行计算。湍流的垂向紊动对流速沿水深分布影响大，将通过不同湍流模式进行分析。

1.2湍流模式

1.2.1 M-Y模式

FVCOM模型中垂向紊动的默认湍流模式为Mellor-Yamada方程。该湍流模式的湍动能和混合长度的方程如下

式中：q2/2为湍动能；l为湍流混合长度；B1，E1，E2为模型闭合常数；Kq为湍流垂向扩散系数，即Kq=0.2lq；垂向涡黏系数Km=lqSm，Sm为稳定函数；壁面函数中的L=(ζ-z)-1+(H+z)-1；κ为卡门常数，即κ=0.4；Fq，Fl分别为湍动能和混合长度的水平扩散项。为减小水平扩散影响，两者取值均为0。

水面和底部的边界条件：

式中：uτs,uτb分别为水面和底部的摩阻流速。

1.2.2 k-ε模式

k-ε湍流模式适合高雷诺数下水流紊动的求解。为分析涌潮水流的强紊动特征，采用该湍流模式进行水体紊动强度的分析。对于k-ε湍流模型可表示为

式中：k为湍流动能；ε为湍流耗散率；垂向涡黏系数Km=cμk2/ε；cμ，c1，c2，k和ε分别为0.09、1.44、1.92、1.00和1.30。

水面条件：

底部的边界条件：

1.3水流边界

对于涌潮水流的表面，水平速度的垂向梯度为0。垂向速度按下式给出：

对于水流的底边界，水平流速的分布和水深、底部切应力以及垂向涡黏系数有关，按式(13)确定。垂向速度按式(14)计算。

式中：τbx,τby分别为x,y方向底部切应力。

底部切应力按如下关系进行计算：

式中：Cd为底部摩阻系数；ρ0为水的密度；ub,vb分别为x,y方向床面的流速。

在FVCOM模型中，底部摩阻系数默认采用式(16)。

式中：z0b为床面粗糙度，取为2.5d50，d50为床面泥沙的中值粒径；z1为近底层网格中心到底部的距离。

根据已有钱塘江河口涌潮水流的数值研究结果，钱塘江河床糙率偏小。在涌潮平面运动的数值模拟中，一般采用较小糙率系数的曼宁公式即式(17)进行底部摩阻系数的计算。

式中：n为曼宁糙率系数，反映床面粗糙程度。

1.4离散处理

考虑到有限体积法能保证计算区域物理量的守恒，模型控制方程采用有限体积法进行数值离散。对流项的空间离散采用二阶精度的计算格式，时间步进采用二阶精度的龙格库塔法，垂向速度采用隐式格式进行求解。模型能很好地计算水跃等强间断水动力问题[13]。该模型在模拟涌潮水流的突变等性质方面具有一定优势，将利用该开源模型研究不同湍流模式下钱塘江河口水流的三维运动特征。

2 模型验证

2.1模型计算范围

为模拟涌潮从生成到衰减过程的水流变化特征，模型计算区域从涌潮生成段的澉浦附近开始到衰减段的闸口。模型计算范围见图1，其中东西向长为89 120 m，南北向宽为28 840 m。涌潮传播速度和网格划分的分辨率有关，高分辨率网格能细化局部地形[5]。另外，受河口平面形态和沙坎影响，涌潮在传播到盐官时强度达到最大。为俘获涌潮传播过程中的最大流速，水平网格的分辨率从盐官区域的50 m向上下游边界逐渐增大到100～400 m。模型计算区域网格划分的单元为45 010个，节点为23 306个。

图1 模型计算范围和观测站点的位置Fig. 1 Computational domain and locations of measured stations

2007年10月25日12:00～30日12:00在钱塘江涌潮河段进行了12个站点潮流数据的测量，并利用潮位观测站点进行同步潮位的测量，潮位和潮流观测站点布置如图1所示。在无涌潮时每小时记录一次潮位数据，涌潮到达后每1～2分钟记录一次数据。对于潮流的观测，每个站位在水深大于4 m时使用垂向6点法进行测量，即分别位于表层(距离水面0.5 m)、0.2倍水深、0.4倍水深、0.6倍水深、0.8倍水深和底层(距离床面0.5 m)。无涌潮时，每小时记录一次流速数据，涌潮到达前后每分钟记录一次流速数据。

上、下游开边界根据实测潮位给定。模型计算开始时刻，区域内的潮位和流速均设为0。垂向分12层。采用模型中已有的内外模分裂算法，外模计算时间步长为0.1 s，内模为1.0 s。模型计算时段从2007年10月25日00:00开始到10月31日00:00结束，模型验证从计算后12小时即10月25日12:00开始以消除初始启动影响。考虑到涌潮水流模拟计算的耗时性，采用刀片服务器进行并行计算，对钱塘江从澉浦附近到闸口的涌潮河段进行三维水流模拟。

2.2数值验证

2.2.1 强涌潮生成

为复演盐官站强涌潮到达时间和水位的猛增过程，利用不同底部摩阻系数类型公式进行模型的率定。图2给出了不同类型阻力系数计算公式(16)和(17)中底摩阻系数在模型区域的取值分布范围。可以看出，在曼宁糙率系数n=0.009 5时，底摩阻系数分布在0.000 37～0.001 9之间。

考虑到模型的计算采用分裂算法，即三维模型通过二维模型得出的潮位ζ进行求解。而在二维模型中，底部摩阻的大小直接影响涌潮高度和到达时间的模拟结果。图3给出了利用不同底部切应力公式进行数值计算后盐官站点10月28日涌潮到达时刻水位的比较。从图3可以看出，在较大的底部摩阻系数下，盐官站涌潮到达时间落后于较小底摩阻系数下的结果。同时，生成的涌潮高度低于较小底摩阻系数下的潮位值。在三维模型的控制方程中，底部切应力作为二阶项对流速垂向分布影响大，但对水位和平面流速的影响小。结合M-Y湍流模式对计算时段中模型区域测量站点的潮位和各层潮流进行了验证。

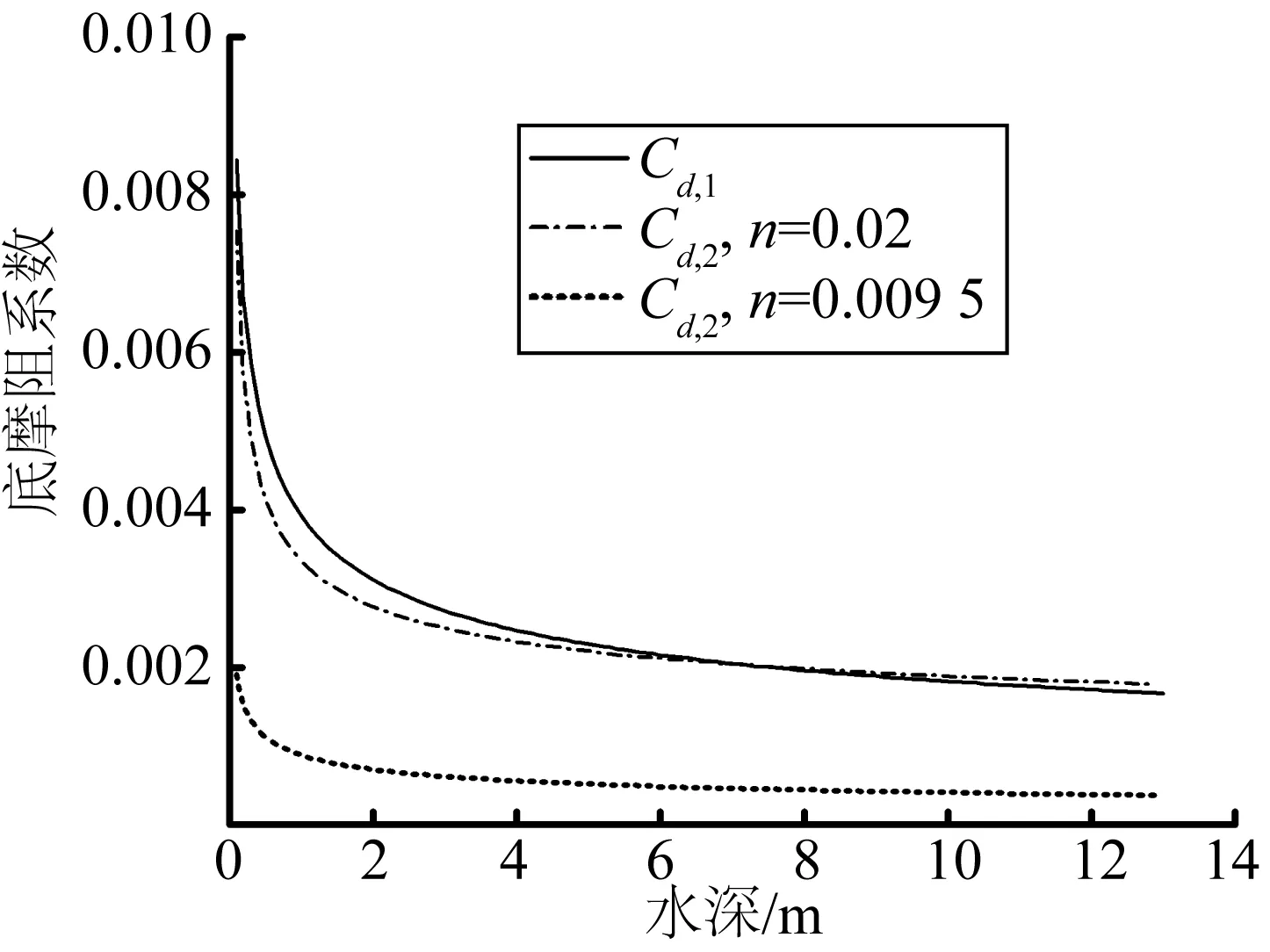
图2 不同类型底部摩阻系数的分布Fig. 2 Distribution of different types of bottom friction coefficient

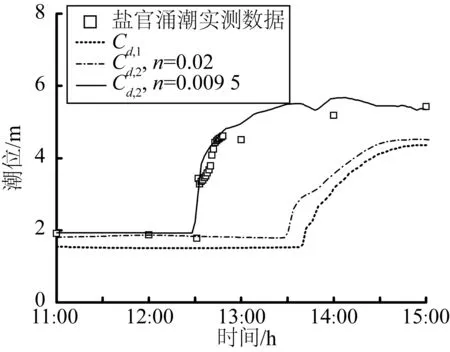
图3 涌潮到达时刻水位比较Fig. 3 Comparison of water level at the arrival time of tidal bore

2.2.2 潮位和潮流

为验证模型在计算涌潮传播过程中水流结果的可靠性，结合M-Y湍流模式对五天涨落潮过程中的全部测量站点的计算结果与实测资料进行了对比。图4为计算区域中强涌潮段盐官和大缺口站点的模型计算潮位与实测数据的验证结果，其中曼宁系数取为0.009 5。图中空心框点为实测潮位，实线为模型计算结果。

将模型计算的潮流流速和流向分别与观测数据中的表层、中层(0.6倍水深)和底层进行验证。图5和图6给出了曼宁系数取为0.025时强涌潮站点703和涌潮初始段站点712模型计算的流速和流向与实测数据的对比，其中空心圆点为实测流速，空心方点为实测流向，实线为模型计算结果。

图4 站点的潮位验证Fig. 4 Validation of tidal level at stations

图5 703站点的表、中和底层潮流验证Fig. 5 Validation of tidal current at station 703

图6 712站点的表、中和底层潮流验证Fig. 6 Validation of tidal current at station 712

从站点的潮位、潮流流速和流向的验证结果可以看出，各站点模型计算值和实测值的平均绝对误差较小。703站点表、中、底层流速的相对误差分别为13%、29%、15%；流向的相对误差分别为12%、18%、14%。712站点各层流速的相对误差分别为8%、6%和13%；流向的相对误差分别为13%、14%和16%。模型计算的表、中、底层流速和流向值与实测值基本一致。相对于先前学者的研究结果[5]，本文采用的三维模型能够更好地复演流速的垂向分布特征，较为准确地模拟钱塘江涌潮河段潮流各层变化。

3 数值结果分析

3.1不同湍流模式下涌潮水流的垂向分布

3.1.1 沿程分布

为说明不同湍流模式下水流运动的三维变化特征，提取了图1中模型计算区域盐官纵剖面1涌潮水流流速。图7给出了M-Y和k-ε湍流模式下盐官纵剖面在涌潮到达时流速的垂向分布(图中左侧为钱塘江河口的上游，右侧为下游)。从图7(a)可以看出，在涌潮到达前，上游河道的水位为2.1 m，水流以较小的速度向下游移动。在涨潮过程中随着下游水流向上游区域涌动，下游水流到达盐官段形成强涌潮，水位猛增到4.0 m。涌潮水流的上层流速达到3.5 m/s，并呈现由上层到底层减小的分布特征。从断面的沿程流速分布可以看出，涌潮形成的后方水流以更大的流速向上游运动，其后上部水体的最大流速可达到5.0 m/s，并在水深方向呈现梯度分布。从图7(b)可以看出，k-ε湍流模式在涌潮到达时水位猛增高度比M-Y湍流模式的计算结果偏小0.2 m。另外，k-ε湍流模式在计算涌潮到达同一点时比M-Y湍流模式慢1 000 m。同时，涌潮表面的水流速度低于M-Y湍流模式得出的结果。在强涌潮生成时，潮头后方存在流速较大的水流。由涌潮观测可知，涌潮过后，涨潮流速仍迅速增加，此类为快水现象。从流速的沿程分布可以看出，本文采用的模型能复演在涌潮作用下河段区域的快水。

图7 涌潮到达时刻盐官河段流速垂向分布Fig. 7 Profile velocity of Yanguan along the water depth at the arrival of tidal bores

3.1.2 不同时刻涌潮水流的垂向分布

图8给出了两种湍流模式下涌潮到达前后盐官站在不同时刻流速沿水深的分布，其中图8(a)为M-Y湍流模式计算结果，图8(b)为k-ε湍流模式计算结果。从图中可以看出，在13:30-13:50时刻，两种湍流模式得出的流速分布基本一致。在涌潮达到后的时刻14:00，M-Y湍流模式计算得出的潮位比k-ε湍流模式得出的结果偏高0.2 m。M-Y湍流模式计算得出的流速在14:00时刻比k-ε湍流模式得出的流速偏大。在1小时过后的最高潮位上，M-Y湍流模式计算得出的潮位比k-ε湍流模式得出的结果稍高0.1 m，流速的分布基本一致，沿水深分布存在梯度。在涌潮到达的一段时间内，表层水流以5.0 m/s的速度沿水深呈递减分布，并向上游运动。在15:30时刻以后，涌潮水流强度减弱，呈现一般涨潮流运动特征。潘存鸿等[1]指出在盐官段大于5.0 m/s快水现象出现在涌潮后15 min，持续时间能达到33 min。从涌潮过后不同时刻断面流速的分布可以看出，数学模型很好地模拟了强涌潮区域的快水，给出的盐官强涌潮区域的快水在水深方向存在分布梯度。本文采用的三维模型结合不同的湍流模式能很好地反映出涌潮水流沿水深分布的运动特征。

图8 不同时刻两种湍流模式下盐官站流速垂向分布Fig. 8 Distribution of time-series velocity at Yanguan under two types of turbulence models

图9 不同湍流模式下潮位过程和实测值的对比Fig. 9 Comparison of tidal level under two types of turbulence models

3.1.3 潮位和流速过程与实测值的对比

图9给出了两种湍流模式下盐官站潮位过程和实测值的对比。从图中可以看出，两种湍流模式均反映了涌潮到达时刻水位的猛增过程，但k-ε湍流模式得出涌潮到达时刻的结果比M-Y模式慢6 min。同时，在得到的水位高度上稍低于M-Y模式的结果。图10给出了两种湍流模式下盐官站流速过程和实测值的对比。两种湍流模式得出的流速变化基本一致，但在相位上k-ε湍流模式落后于M-Y湍流模式计算结果。这和涌潮作用下产生的湍流紊动有着紧密的关系。

图10 不同湍流模式下流速过程和实测值的对比Fig. 10 Comparison of velocity under two types of turbulence models

3.2湍动能

为反映不同湍流模式中涌潮作用下水流运动产生差异的内部机理，给出两种湍流模式下在涌潮开始生成和强涌潮处湍动能的变化过程。提取了图1中模型区域涌潮开始生成处的代表站点A和强涌潮处的代表站点盐官的湍动能。图11给出了涌潮开始生成处的代表点A在两种湍流模式下湍动能的变化。图12给出了强涌潮处盐官站点在两种湍流模式下湍动能的变化。

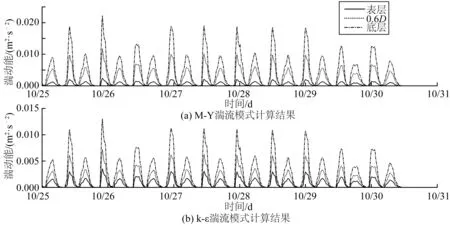
图11 涌潮初始生成处两种湍流模式下湍动能Fig. 11 Turbulent kinetic energy of two types of turbulence models at the initial formation period of tidal bores

从图11可以看出，在涌潮初始生成处，湍动能较小，呈现表层到底层增大的趋势。M-Y湍流模式计算得出的湍动能稍大于k-ε湍流模式的结果。从图12可以看出，在强涌潮生成处，湍动能增大到一个量级以上。M-Y湍流模式得出的湍动能呈现由表、中、底层增大的分布特征。k-ε湍流模式计算得出的湍动能表现为底层和中层较一致，表层小。两种湍流模式给出的湍动能在量级上差异不明显。在强涌潮段，k-ε湍流模式得出的湍动能较大，反映涌潮水流的脉动作用较为强烈。这说明了k-ε湍流模式在盐官段计算得出的涌潮到达时间稍慢于M-Y湍流模式结果的原因。另外，涌潮的强紊动特征使得k-ε湍流模式计算得出的涌潮高度稍低于M-Y湍流模式的计算结果。

图12 强涌潮处两种湍流模式下湍动能Fig. 12 Turbulent kinetic energy of two types of turbulence models under the strong tidal bore

为定量地表示两种湍流模式下湍动能的大小，表1和表2分别给出了M-Y湍流模式和k-ε湍流模式计算得出的最小、最大和平均湍动能。从两表中可以看出，在涌潮初始生成处，M-Y湍流模式计算得出的最大湍动能在中层和底层分别为0.011 7 m2/s2和0.022 2 m2/s2，大于k-ε湍流模式得出的结果。k-ε湍流模式在表层最大湍动能为0.003 5 m2/s2，大于M-Y湍流模式得出的结果。在强涌潮生成处，k-ε湍流模式在表、中和底层的湍动能均大于M-Y湍流模式计算值。可以得出，在涌潮水流的三维模拟中，k-ε湍流模式给出了较强的水流紊动特征，使得在涌潮水位和流速上稍小于M-Y湍流模式的计算结果。

表1M-Y模式计算湍动能

Tab.1TurbulentkineticenergybyturbulencemodelofMellor-Yamada(m2·s-2)

代表点表层中层底层最小最大平均值最小最大平均值最小最大平均值涌潮开始处A点2．18´10-60．00240．00066．78´10-60．01170．00266．51´10-60．02220．0047强涌潮处盐官站2．21´10-50．10760．01295．19´10-50．25110．03016．97´10-50．35490．0425

表2k-ε模式计算湍动能(m2·s-2)

Tab.2Turbulentkineticenergybyturbulencemodelofk-ε(m2·s-2)

代表点表层中层底层最小最大平均值最小最大平均值最小最大平均值涌潮开始处A点2．57´10-60．00350．00083．55´10-60．00720．00165．54´10-60．01300．0029强涌潮处盐官站9．49´10-50．33440．04141．06´10-40．47220．05848．40´10-50．49810．0617

4 结 语

基于有限体积法FVCOM模型，并结合湍流模式对钱塘江涌潮水流的三维运动进行了准确的数值模拟。从三维数值模拟结果的分析可以看出，采用的模型能很好地模拟涌潮到达前后流速的垂向变化特征。通过两种湍流模式下涌潮到达时间和涌潮高度等进行的数值研究分析结果，可以发现，k-ε湍流模式计算得出的涌潮达到时间稍迟、潮位稍低，两种模式计算的涌潮流速分布结果偏差较小，均能模拟涌潮水流三维运动特征。不同湍流模式给出的湍动能在量级上基本一致，在强涌潮作用下水流湍动能比涌潮初始生成段大一个量级以上。通过对钱塘江涌潮水流的三维模拟和湍动能的分析，能为深入认识涌潮水流运动提供技术手段，并为钱塘江河口物质输运提供研究基础。

[1] 潘存鸿, 林炳尧, 毛献忠. 钱塘江涌潮二维数值模拟[J]. 海洋工程，2007, 25(1): 50-56. (PAN Cunhong, LIN Bingyao, MAO Xianzhong. 2D numerical simulation of tidal bore in Qiantang River[J]. The Ocean Engineering, 2007, 25(1), 50-56. (in Chinese))

[2] 李绍武, 卢丽锋, 时钟. 河口准三维涌潮数学模型研究[J]. 水动力学研究与进展：A辑. 2004, 19(4): 407-415. (LI Shaowu, LU Lifeng, SHI Zhong. A quasi 3D numerical model for estuarine tidal bore[J]. Chinese Journal of Hydrodynamics, 2004, 19(4): 407-415. (in Chinese))

[3] 王灿星, 陈菊芳, 金晗辉, 等. 涌潮对钱塘江河道流场影响的三维数值模拟研究[J]. 水动力学研究与进展：A辑. 2012, 27(4): 367-375. (WANG Canxing, CHEN Jufang, JIN Hanhui, et al. Three-dimensional numerical simulation of tidal bore of Qiantang River[J].Chinese Journal of Hydrodynamics, 2012, 27(4): 367-375. (in Chinese))

[4] LIU H, LI J, SHAO S, et al. SPH modeling of tidal bore scenarios [J]. Natural Hazards, 2015, 75(2): 1247-1270.

[5] 谢东风, 潘存鸿, 吴修广. 基于FVCOM模式钱塘江河口涌潮三维数值模拟研究[J]. 海洋工程, 2011, 29(1): 47-52. (XIE Dongfen, PAN Cunhong, WU Xiuguang. Three-dimensional numerical modeling of tidal bore in Qiantang based on FVCOM[J]. The Ocean Engineering, 2011, 29(1), 47-52. (in Chinese))

[6] 陈永平, 刘家驹, 喻国华. 潮流数值模拟中紊动黏性系数的研究[J]. 河海大学学报：自然科学版, 2002, 30(1): 39-43. (CHEN Yongping, LIU Jiaju ,YU Guohua. A study on eddy viscosity coefficient in numerical tidal simulation[J]. Jounal of Hohai University, 2002, 30(1): 39-43. (in Chinese))

[7] CHANSON H, TAN K. Turbulent mixing of particles under tidal bores: An experimental analysis [J]. Journal of Hydraulic Research, 2010, 48(5): 641-649.

[8] DOCHERTY N J, CHANSON H. Physical modeling of unsteady turbulence in breaking tidal bores [J]. Journal of Hydraulic Engineering-ASCE, 2012, 138(5): 412-419.

[9] LU B P, CHANSON H, GLOCKNER S. Large eddy simulation of turbulence generated by a weak breaking tidal bore [J]. Environmental Fluid Mechanics, 2010, 10(5): 587-602.

[10] XIE Dongfeng, PAN Cunhong. A preliminary study of the turbulence features of the tidal bore in the Qiantang River, China [J]. Journal of Hydrodynamics, 2013, 25(6): 903-911.

[11] 熊伟, 朱志夏, 董佳, 等. 湍黏系数对浅滩海域三维风暴潮的影响[J]. 水利水运工程学报, 2014(6): 45-51. (XIONG Wei, ZHU Zhixia, DONG Jia, et al. Effects of turbulent viscosity coefficient on 3-D storm surge within shallow seas[J] Hydro-Science and Engineering, 2014(6): 45-51. (in Chinese))

[12] GUSEV A V, LYAPIDEVSKII V Y. Turbulent bore in a supercritical flow over an irregular bed [J]. Fluid Dynamics, 2005, 40(1): 54-61.

[13] HUANG H, CHEN C S, COWLES G W, et al. FVCOM validation experiments: Comparisons with ROMS for three idealized barotropic test problems [J]. Journal of Geophysical Research-Oceans, 2008, 113(C07): 1-14.

Three-dimensional simulation of tidal bore in the Qiantang estuary under different turbulence models

WANG Qiushun1, 2, 3, PAN Cunhong1, 2, 3

(1. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China; 2. Zhejiang Institute of Marine Planning and Design, Hangzhou 310020, China; 3. Key Laboratory of Estuarine and Coast of Zhejiang Province, Hangzhou 310016, China)

TV148

A

10.16483/j.issn.1005-9865.2017.01.009

1005-9865(2017)01-0080-10

2016-04-21

国家自然科学基金资助项目(51379190；41306082)

汪求顺(1984-)，男，安徽桐城人，博士，主要从事河口海岸动力学研究。E-mail:wangqiushun57@163.com