改进型中心管模型能量转换性能试验及样机设计

吴必军，李 猛, 4，陈天祥, 4，伍儒康, 4

(1.中国科学院可再生能源重点实验室，广东 广州 510640; 2. 广东省新能源和可再生能源研究开发与应用重点实验室，广东 广州 510640; 3. 中国科学院广州能源研究所，广东 广州 510640; 4. 中国科学院大学，北京 100049)

改进型中心管模型能量转换性能试验及样机设计

吴必军1, 2, 3，李 猛1, 2, 3, 4，陈天祥1, 2, 3, 4，伍儒康1, 2, 3, 4

(1.中国科学院可再生能源重点实验室，广东 广州 510640; 2. 广东省新能源和可再生能源研究开发与应用重点实验室，广东 广州 510640; 3. 中国科学院广州能源研究所，广东 广州 510640; 4. 中国科学院大学，北京 100049)

为了提高中心管振荡水柱波浪能利用技术能量转换效率，基于新的认识和目前常用的2.4米导航灯标，对中心管尾部设计了三种模型并在造波水槽中进行能量转换性能试验。试验结果表明：直管型中心管俘获宽度比最高达到了70.25%，但通频带宽度窄；加长喇叭口型中心管略好于喇叭口型中心管；在喷咀比为0.02条件下，加长喇叭口型中心管浮体有较高双峰俘获宽度比，波峰为40.0%，波谷为31.6%，通频带宽，为随机波下高效转换创造了条件。最高俘获宽度比和双峰通频带特性实验数据结果都优于历史文献值。根据试验数据对一些适合小型海洋仪器供电的样机进行了设计，设计的样机具有较高的性价比。

波浪能；中心管；振荡水柱；俘获宽度比；海洋仪器；波力发电

Abstract: In order to improve the energy conversion efficiency of the centre pipe energy conversion technology, three models with different bottom shapes based on the new understanding and the current 2.4 m wave power navigation light were designed for experimental study in the wave tank. The experimental results are presented. For the straight pipe buoy, the maximum capture width ratio (CWR) is 70.25%, but presents narrow bandwidth. The CWR of the lengthen-horn center pipe buoy is slightly better than that of the horn center pipe buoy. Under the condition of the nozzle ratio 0.02, the CWR of the lengthen-horn center pipe body presents higher double peaks, 40.0% at peak and 31.6% at trough. The curve of the CWR is relatively flat. The higher double-peak CWR of the lengthen-horn center pipe buoy will create conditions for high efficient conversion under random waves. The peak CWR and the bandwidth of those data are superior to that of the historical documents. Based on the experimental results, some prototypes for power supplies for oceanographic instruments have been presented. The prototypes are more cost-effective.

Keywords: wave energy; centre pipe; oscillating water column; capture width ratio; oceanographic instruments; wave power

二十世纪四十年代中期，日本的益田善雄[1]提出了中心管振荡水柱波力发电技术。基于该技术开发的航标灯用波力发电装置是目前世界上唯一一种波浪能商业化产品，也是将来海洋观测仪器供电的一个重要选择。中心管振荡水柱波力发电技术由一个轴对称旋转浮体、空气透平和发电机构成。轴对称旋转浮体中间掏空带有一根管道，管道内液面和空气透平之间形成一气室。该种技术具有结构简单、制造成本低、可维护性强、海生物附着影响小、可靠性高等优点。

影响中心管振荡水柱技术转换效率的因素很多，浮体的水下形状(凸形、平底形)、管道的大小和形状是一些重要因素[2]。早期能量转换理论研究往往采用一些简化形状，随着计算能力的大幅提升，目前对稍复杂形状的中心管技术也进行了数值计算研究[3-7]。这些理论研究给出了附加质量、阻尼系数、波浪激励力等，也预测到能量转换特性有双峰值出现，为实验研究提供了基础数据。国外实验研究成果资料查到的较少，较多的是国内实验研究成果。1982年吴雄建等[8]对多种尾部形状中心管浮标进行转换效率研究，效率出现了双峰值，但遗憾的是实验数据表明最高俘获宽度比(类似转换效率)不到5%。1983年蔡国民[9]研制了直径2.4米的波力发电浮标，进行了陆上和海上试验，海上试验表明从波浪能到电能的转换效率还不到1%。1984年吴藻华等[2]研究水下浮体形状对波能转换效率影响，俘获宽度比实验值最高约为16%，而且通频带较窄。同年Whittaker等[10]对一个直径3米、中心管直径0.7米的发电浮标1/10模型进行了试验，试验研究表明俘获宽度比最高达到了50%，但通频带很窄，阻尼变小后通频带变宽，出现了双峰值，但出现双峰值时俘获宽度比最高为11%左右。1987年，何明楷等[11]根据需求设计了最佳参数的波力发电灯浮标，试验研究发现中心管的长度较大是有利的，喷嘴比的影响也很大。1994年，黄国樑等[12]针对前期研究的发电浮标在波浪周期短、波高小发电量不能满足需求的条件下对2.4米浮标的发电性能进行了进一步试验研究，研究表明通过减少发电浮标质量移动了最佳响应波周期，但俘获宽度比未见提高，最高大概为14.6%，通过适当加长和加粗中心管可提高俘获宽度比，最高达到了25%。显然这期间试验研究结果最好的俘获宽度比为50%。由于学者们基于航标稳性要求，普遍认为该技术是浮体几乎不动，波浪能量仅靠气室内的水柱运动转换能量，理论上无法达到较高的转换效率。因此，从1994年后，有关中心管振荡水柱技术试验研究国内外鲜有文献报道。

文献表明，国内外对中心管技术的理论和实验都有一定的研究，得到了一些重要结论，但由于当时实验条件限制，只测试了一些峰值(比如中心管液位的最高值和最低值)，对中间过程采用正弦值假设，得到的气体流量等参数与实际(周期变化，不一定是正弦变化)有出入，数据不精准，而且实测的俘获宽度比最高不超过50%。另外，笔者认为，作为能量转换主体的浮体在波浪作用下是一个机械振动体，按照振动理论，有条件获得较大的机械能，中心管波力发电技术应该表现出比历史资料更高的转换效率。为此基于新的认识和直径2.4米、中心管直径0.7米、型号BHF2-2.4-0.7D1发电浮标，提高测量精准度，按5∶1比例进行缩小设计了三种不同中心管底部形状的振荡水柱式波能转换浮体，在水槽中测试其在不同波浪周期下的能量转换效率，以期得到比历史资料更好的实验成果，为低成本开发中心管振荡水柱波力发电装置提供基础数据。

1 实验装置及数据处理方法

试验是在造波水槽中进行的，水槽尺寸为1.2 m×1.2 m×50 m(宽×高×长)。水槽一端装有计算机控制的变频电源伺服电机驱动的推板式造波机，推板宽1.16 m，高1.2 m，可造规则波和不规则波；另一端为端部消波装置，水槽中间部分为试验段，通过此处的玻璃墙可以清楚地观察装置的运动情况。图1为实验装置示意图；图2是实验实物图。

在距离造波机大约8 m处装有一电容式浪高仪，可以测量入射波波高和周期；在距离造波机约17 m处放置试验模型，在模型气室顶部开有一气孔作为阻尼，安装有一只电容式浪高仪，用于测量气室内水位的相对波动；气室顶部还装有测压口，用PY301差压变送器测量气室内相对压力。入射波的波高数据由SDA1000传感器数据采集系统采集，由计算机控制，采样频率为20 Hz；气室内的水位变化和气压相对变化被相应的传感器获取，通过采集卡进行同步采样，由计算机控制，采样频率为16 Hz。

本实验模型输出的平均气动功率Pair由气室内外气体压力差和气室内液位算出。气室内液位由浪高仪测出，压力差由压力差传感器测出，其计算公式[13]：

式中：ΔPi为第i次采样时气室内压力差，Pa；hi,hi+1为第i和i+1次采样时气室内水位，m；S为气室水线截面积，m2；n为采样总次数；Δt为采样时间间隔，s。

入射波功率PW采用深水波计算公式，计算公式[13]：

式中：HO为入射波浪高，m；T为入射波周期，s；B为浮体迎波宽度，m。浪高仪测出波高和波周期。

俘获宽度比(capture width ratio，简称CWR)定义为：

气室平均气流量Qav：

气室平均气压ΔPav：

图1 实验装置简图Fig. 1 Diagram of the experiment device

图2 模型在水槽中的实验照片Fig. 2 Photo of model C in the wave tank

2 模型试验方案

影响中心管俘获宽度比的因素很多，包括入射波的周期、波高、中心管的形状、浮体的吃水深度等。主要探究中心管尾管结构对俘获宽度比的影响，参照浮标“BHF2-2.4-0.7D1”的尺寸进行缩小，缩尺比为5，得到直管口(A模型)，在此基础上设计了另外2个模型——喇叭口(B模型)和加长喇叭口(C模型)。三种试验模型简图、主要参数和实物如图3所示。

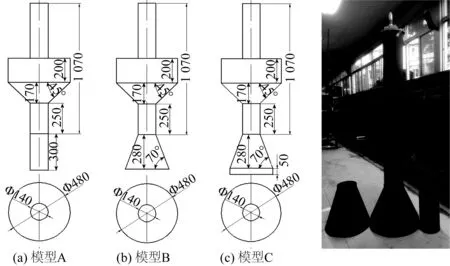
图3 三种模型简图和照片Fig. 3 Sketch of three models and the photo

为了节省成本，模型制作成可拆卸的，浮体上部分三个模型共用一个，尾部的不同部分制造成三个。为探索浮体吃水深度和喷咀比对俘获宽度比的影响，也设计了一些方案进行试验。总的试验方案如表1所示。为保证试验所测数据的准确性，提高试验的可信度，在每一个试验条件下都重复试验三次。

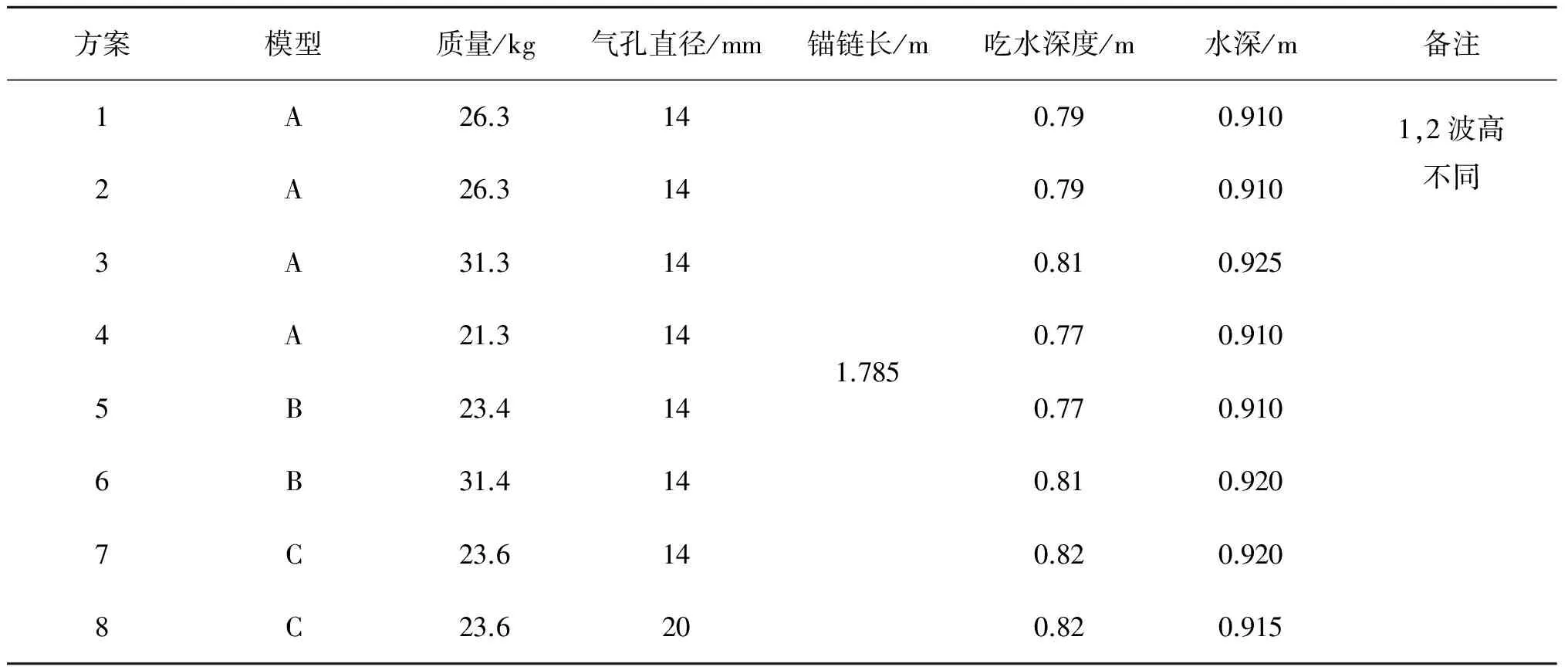
表1 试验方案Tab. 1 Test cases

3 模型试验结果

表1列出了实验方案，方案1～方案7喷气孔面积与气室面积之比(喷咀比)为0.01，而对于方案8，喷咀比为0.02，表2列出了测得最高俘获宽度比时的一些参数。在造波水槽中，推板运动的推程(推板运动范围的一半)和周期影响着波浪高度。

图4是在推程为20 mm条件下波高随周期的变化情况及在此波高下A模型的俘获宽度比，图中每个周期下测量3次，有3个值，分别用“1、2、3”表示，3个值有个平均值，用“average”表示(后面图5～图11含义一样)。图5是在推程为25 mm条件下波高随周期的变化情况及在此波高下A模型的俘获宽度比。图4俘获宽度比最高为49.97%，图5俘获宽度比最高为53.79%(见表2)。两者比较，不同波高得到的俘获宽度比略有不同，在同一周期下，恰当的波高可使装置获得较高的俘获宽度比。

图4 20 mm推程产生的波高及A模型俘获宽度比Fig. 4 Wave height caused by the 20 mm travel and the CWR of A model

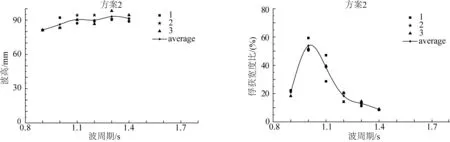
图5 25 mm推程产生的波高及A模型俘获宽度比Fig. 5 Wave height caused by the 25 mm travel and the CWR of A model

图6是吃水较深时A模型在对应波高下的俘获宽度比，此时俘获宽度比最高达到了70.25%(见表2)。图6造波波高偏小，是因为浮体运动接近共振，运动幅度过大，波高稍大会导致模型运动幅度过大，发生越浪现象。图7是吃水较浅时A模型在对应波高下的俘获宽度比，实验值最高为38.01%，几乎只是图6中最大值的一半。

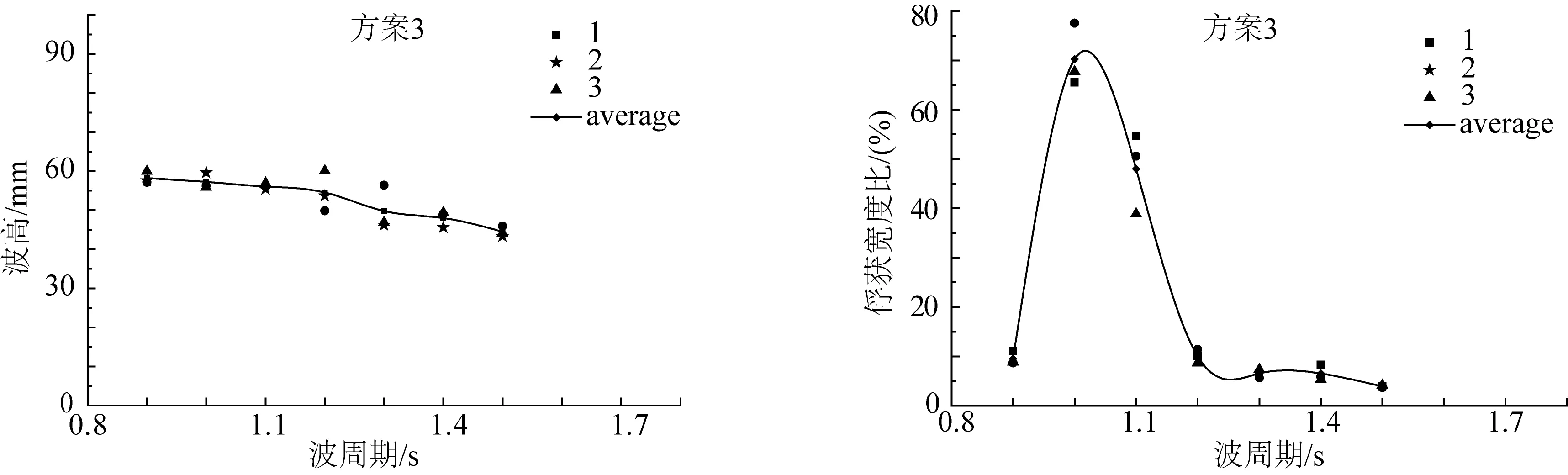
图6 入射波高及对应的A模型吃水较深时俘获宽度比Fig. 6 Incident wave height and the corresponding CWR of A model when deep draft

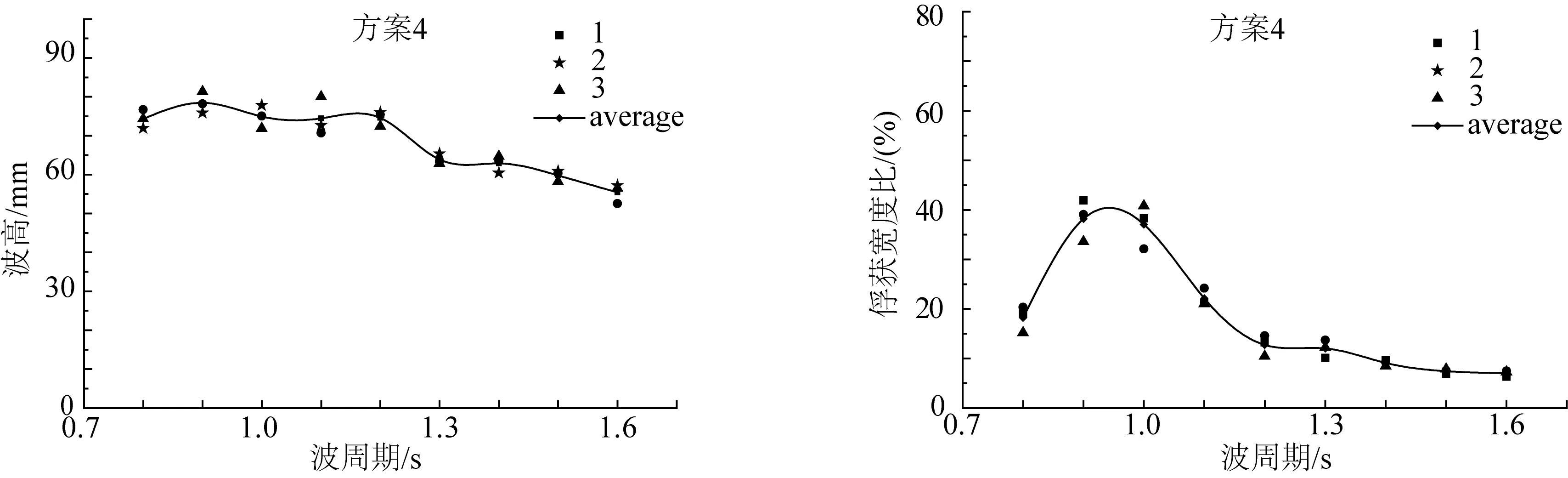
图7 入射波高及对应的A模型吃水较浅时俘获宽度比Fig. 7 Incident wave height and the corresponding CWR of A model when shallow draft

图8是吃水较浅时B模型在对应波高下的俘获宽度比，此时俘获宽度比最高达到了31.03%(见表2)，明显出现了双峰值，但波谷较低，大概为15%。图9是吃水较深时B模型在对应波高下的俘获宽度比，此时俘获宽度比最高达到了31.48%(见表2)，也明显出现了双峰值，波谷较高，大概为30%。图8和图9比较，质量增加，不仅俘获宽度比有所增加，而且峰值周期向着增大的方向发展。

图8 入射波高及B模型吃水较浅时的俘获宽度比Fig. 8 Incident wave height and the corresponding CWR of B model when shallow draft

图9 入射波高及B模型吃水较深时的俘获宽度比Fig. 9 Incident wave height and the corresponding CWR of B model when deep draft

图10是在喷咀比为0.01时C模型在对应波高下的俘获宽度比，也出现了双峰值，其俘获宽度比最大为30.91%(见表2)，波谷为22.57%。从表1可知，方案7的工况同方案5基本一致，此时图10俘获宽度比比图8整体上略有提高。图11是在喷咀比为0.02时C模型在对应波高下的俘获宽度比，也出现了双峰值，其俘获宽度比最大为40.15%(见表2)，波谷为31.6%，此值相比文献[4]几乎提高了4倍。

图10 入射波高及对应的C模型在喷咀比为0.01时的俘获宽度比Fig. 10 Incident wave height and the corresponding CWR of C model when the nozzle ratio is 0.01

图11 入射波高及对应的C模型在喷咀比为0.02时的俘获宽度比Fig. 11 Incident wave height and the corresponding CWR of C model when the nozzle ratio is 0.02

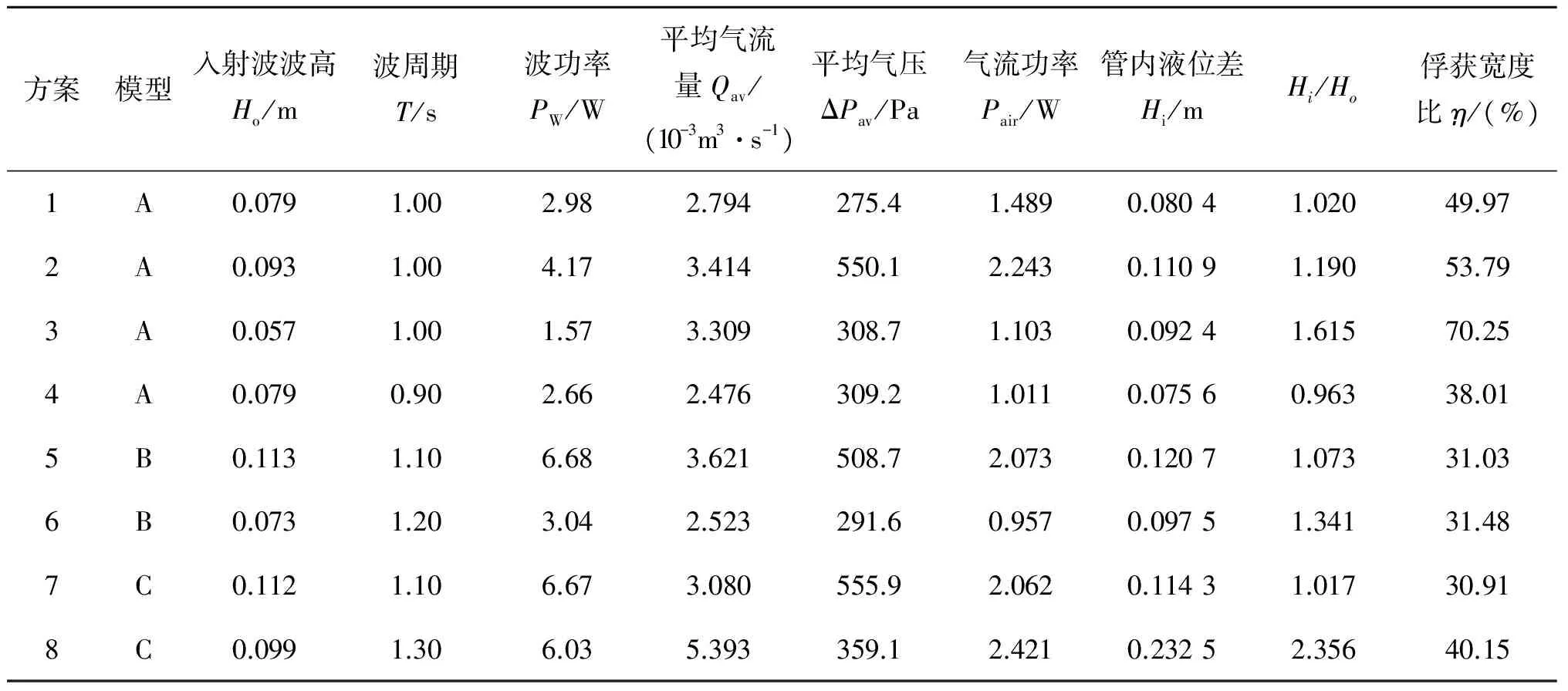
方案模型入射波波高Ho/m波周期T/s波功率PW/W平均气流量Qav/(10-3m3·s-1)平均气压ΔPav/Pa气流功率Pair/W管内液位差Hi/mHi/Ho俘获宽度比/(%)1A0．0791．002．982．794275．41．4890．08041．02049．972A0．0931．004．173．414550．12．2430．11091．19053．793A0．0571．001．573．309308．71．1030．09241．61570．254A0．0790．902．662．476309．21．0110．07560．96338．015B0．1131．106．683．621508．72．0730．12071．07331．036B0．0731．203．042．523291．60．9570．09751．34131．487C0．1121．106．673．080555．92．0620．11431．01730．918C0．0991．306．035．393359．12．4210．23252．35640．15

4 样机设计

基于文献[12]和上文的试验研究结果，设计了一些样机并进行比对，如表3所示。

表3 文献[12]设计的发电浮标特性与新型发电浮标特性比较Tab. 3 Features of the new wave power floating buoy and compared with that of the buoy designed in the literature [12]

文献[12]设计了一个波浪能发电浮体，浮体直径为2.4 m，中心管直径为0.7 m，质量为4 000 kg，在周期为2.7 s、波高为0.25 m时，入射波功率为405 W时输出气动功率为59 W。基于A模型，依据图6的模型测试结果和相似理论，当模型放大4倍时得到新型浮标1，新型浮标1直径为1.92 m，中心管直径为0.56 m，质量为2 003 kg，在波峰周期2.0 s、波高为0.23 m条件下，输入波功率为203 W，按波峰70.25%俘获宽度比计算，可输出气动功率为142 W，是文献资料59 W[12]的2.4倍。基于相似理论和图6可算出模型放大5倍时新型浮标2的气动输出功率，如表3所示。同理，基于C模型，依据图11的模型测试结果，当模型放大4倍时得到新型浮标3，新型浮标3直径为1.92 m，中心管直径为0.56 m，质量为1 510 kg，在波谷周期2.4 s、波高为0.4 m条件下，输入波功率为737 W，按波谷31.6%俘获宽度比计算，可输出气动功率为233 W，在同样2.4 s周期下，如果波高为0.25 m，可输出气动功率为91 W，是文献资料59 W[12]的1.54倍。如果透平机组的转换效率为40%，那么浮标可输出电功率为36.4 W，可满足一般海洋仪器耗电要求，更重要的是超过31.6%效率的区间大概为2.04～2.72 s，在不规则波下有较高的转换效率。同理可算出模型放大5倍时新型浮标4的气动输出功率，如表3所示。显然，新型浮标4输出气动功率在几乎相同条件下(波高0.25 m、周期2.7 s)是文献[12]浮标输出气动功率的的2.15倍，但质量减少了1 000 kg，如果波高提高到0.5 m，入射波功率提高了4倍，输出气动功率可达508 W，是文献[12]浮标输出气动功率的的8.6倍。相对历史资料而言，基于本文提供的试验研究成果进行波力发电浮标设计，得到的发电浮标较轻、尺度较小、输出功率相对大，有较高的经济效益。在不同海况使用、有不同供电需求的发电浮标可依据相似定律进行设计。

5 结 语

浮标的吃水深度、喷咀比、尾部形状等许多因素影响着中心管振荡水柱技术的俘获宽度比，适当地优化这些参数有利于提高该技术的俘获宽度比。模型试验表明，直管型模型俘获宽度比目前测试最高达到了70.25%，但响应周期窄，在波况比较规则的海区使用有较高的转换效率，适用于波浪周期比较单一的海区使用；加长喇叭口模型的俘获宽度比尽管最高值只达到了40.15%，但双峰值的出现极大地拓宽了通频带，有利于提高波力发电浮标在随机波条件下的转换效率。本文试验得到的最高俘获宽度比和双峰通频带特性都优于历史文献值，试验结果为降低中心管振荡水柱发电装置的建造成本和对应的布放成本提供了依据。

[1] HEATH T V. A review of oscillating water columns[J]. Philos Trans R Soc A-Math Phys Eng Sci, 2012, 370(1959):235-245.

[2] 吴藻华, 夏洪峰, 戴李民. 浮体形状对波能转换浮标性能的影响[J].海洋工程, 1984, 2 (4): 59-62.(WU Zaohua, XIA Hongfeng, DAI Limin. Floating body shape influence on the properties of wave energy conversion [J]. The Ocean Engineering, 1984, 2(4):59-62. (in Chinese))

[3] MCCORMICK M E. Analysis of a wave energy conversion buoy[J]. Journal of Hydronautics, 1974, 8(3): 77-82.

[4] WHITTAKER T J T, MCPEAKE F A. Design optimization of axi-symmetric tail tube buoys[M]//Hydrodynamics of Ocean Wave-Energy Utilization. 1985: 103-111.

[5] HONG D C, HONG S Y, HONG S W. Numerical study of the motions and drift force of a floating OWC device[J]. Ocean Engineering, 2004, 31(2): 139-164.

[6] ALVES M A, COSTA I R, SARMENTO A J N A, et al. Performance evaluation of an axysimmetric floating OWC[C]//Proceeding of the 20th International Offshore and Polar Engineering Conference. 2010: 856-862.

[7] GOMES R P F, HENRIQUES J C C, GATO L M C, et al. Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion[J]. Renewable Energy, 2012, 44: 328-339.

[8] 吴雄建, 糜振星, 等. 波浪发电浮标浮体的试验研究[J]. 新能源, 1982, 11(4): 31-37.(WU Xiongjian, MI Zhenxing, et al. Experimental study of the floating wave power body[J]. New Energy, 1982, 11(4):21-37. (in Chinese))

[9] 蔡国民. 灯浮标用波力发电装置[J]. 水运工程, 1983(4): 47-49. (CAI Guomin. Wave power device for navigation light[J]. Port & Waterway Engineering, 1983(4):47-49. (in Chinese))

[10] WHITTAKER T J, MCLLHAGGER D S, BARR A G. Wells turbines for navigation buoys[M]//Energy for Rural and Island Communities. 1984: 289-297.

[11] 何明楷, 陈加菁, 蔡丽华, 等. 选择大型波力发电灯浮标最佳参数的试验研究[J]. 海洋工程, 1987, 5 (4): 84-90. (HE Mingkai, CHEN Jiajing, CAI Lihua, et al. Experimental study on the optimal parameters of the large wave power navigating buoy [J]. The Ocean Engineering, 1987, 5(4):84-90. (in Chinese))

[12] 黄国樑, 冯伯俊, 刘天威, 等. 改进波浪发电浮标性能的试验研究[J]. 海洋工程, 1994, 12(1): 104-110. (HUANG Guoliang, FENG Bojun, LIU Tianwei, et al. An experimental study for improving the performance of a wave energy conversion buoy[J]. The Ocean Engineering, 1994, 12(1):104-110. (in Chinese))

[13] 梁贤光, 王伟, 杜彬, 等. 后弯管波力发电浮标模型性能试验研究[J]. 海洋工程, 1997, 15(3): 78-87. (LIANG Xianguang, WANG Wei, DU Bin, et al. Experimental research on performance of BBDB wave-activated generation device model[J] . The Ocean Engineering, 1997, 15(3):78-87. (in Chinese))

An experimental study on energy conversion of the modified centre pipe buoy and the design of prototypes

WU Bijun1, 2, 3, LI Meng1, 2, 3, 4, CHEN Tianxiang1, 2, 3, 4, WU Rukang1, 2, 3, 4

(1. Key Laboratory of Renewable Energy, Chinese Academy of Sciences, Guangzhou 510640, China; 2. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China; 3. Guangzhou Institute of Energy Conversion, CAS, Guangzhou 510640, China; 4. University of Chinese Academy of Sciences, Beijing 100049, China)

P743.2

A

10.16483/j.issn.1005-9865.2017.01.011

1005-9865(2017)01-0097-08

2016-03-02

国家自然科学基金(51579231；51276185)

吴必军(1965-)，男，研究员，博导，主要从事海洋波浪能转换技术研究。E-mail: wubj@ms.giec.ac.cn