基于小波分析的FastICA联合降噪方法在滚动轴承故障诊断中的应用研究

吴雅朋 王吉芳 徐小力 蒋章雷

北京信息科技大学现代测控技术教育部重点实验室，北京，100192

基于小波分析的FastICA联合降噪方法在滚动轴承故障诊断中的应用研究

吴雅朋 王吉芳 徐小力 蒋章雷

北京信息科技大学现代测控技术教育部重点实验室，北京，100192

采用小波分析方法进行振动信号降噪存在选取参数依靠经验的问题，采用独立分量分析(ICA)方法进行振动信号降噪存在欠定问题，为了避免小波降噪以及ICA方法单独使用的缺点，提出了将小波降噪分析和基于负熵的FastICA独立分量分析相结合来处理滚动轴承含噪振动信号的方法。首先对原始信号进行小波降噪处理，然后将处理后的信号与原始信号组成FastICA的输入矩阵，进行FastICA降噪处理，最后利用滚动轴承振动信号对该方法进行有效性验证。实验分析表明：该方法增大了振动信号的峭度值，达到了滚动轴承振动信号降噪的目的。

小波分析；独立分量分析；降噪；滚动轴承

0 引言

滚动轴承原始振动信号因受工作环境的影响而夹杂噪声，尤其是在轴承早期故障诊断中，信号通常都非常微弱，所以，信号降噪处理在提高滚动轴承振动信号故障诊断准确度中占据着重要地位。

在对振动信号进行降噪处理时，传统的降噪方法主要包括非线性滤波和线性滤波，其中最为典型的代表是中值滤波和Wiener滤波。传统去噪方法的不足之处在于：信号处理变换后的熵增高，无法刻画信号的非平稳性并且无法得到信号的相关性[1-2]。为了克服这些局限性，国内外学者在振动信号方面展开了大量的研究。钱征文等[3]提出了一种根据噪声信号的快速傅里叶变换结果来决定有效秩阶次，以降噪信号的信噪比和均方差大小为依据确定重构矩阵的结构奇异值分解方法。沈路等[4]研究了广义数学形态滤波器在脉冲噪声与随机噪声干扰下的降噪效果，成功将广义数学形态滤波器用于机械工程振动信号处理中，提高了信噪比，达到了提取信号细节和抑制噪声的目的。

本文提出小波分析和基于负熵的独立分量分析(FastICA)(以下简称“小波-FastICA”)联合降噪方法，该方法将采集到的单通道振动信号进行小波分析预处理，得到小波降噪信号，构建虚拟振动信号通道；将原始振动信号和虚拟振动信号组成输入矩阵，采用基于负熵的FastICA算法进行信号的降噪处理。

1 小波-FastICA联合降噪方法的基本原理

1.1小波分析信号处理方法

小波分析方法是一种窗口大小固定、形状可变的时频局部化信号分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低频率分辨率，即小波分析方法对信号具有自适应性。设长度为n的信号f(n)被噪声s(n)所污染，所测得的含噪声数据

x(n)=f(n)+s(n)

(1)

小波降噪处理的目的就是从含噪数据x(n)中得到信号f(n)的一个逼近信号，使其在某种误差下为f(n)的最优逼近[5]。

在设备的实际运转中，所获得的有用信号通常为一些低频信号或平稳信号，而噪声信号则表现出高频以及非平稳的特征。信号去噪的好坏取决于以下几个环节：小波基的选择、小波分解层数的确定、阈值函数以及阈值估计方法的选取。其中最关键的环节是如何选取阈值和如何对阈值进行量化，从某种程度上说，阈值的选择直接关系到信号去噪的优劣。对小波阈值降噪来说，其阈值的选择规则一般有以下几种：①固定阈值(sqtwolog)；②基于史坦的无偏似然估计原理(SURE)的自适应阈值选择(rigrsure)；③启发式阈值(heursure)；④极大极小值(minimaxi)。

将高斯白噪声作为一种信号进行去噪时发现，阈值规则②和④比较保守，当含噪声信号的高频信息有很小一部分在噪声范围内时，这两种阈值非常有用，可以将微弱的信号提取出来；而阈值规则①和③去噪比较完全，去噪时显得更为有效，但是很容易把有用信号的高频信号当作噪声而去除[6]。

在使用小波阈值降噪时，为了得到更好的去噪效果，不但要选择合适的小波函数，还要确定最佳的分解层数并选取合适的阈值。为了得到最好的去噪效果，需要改变所取的小波函数、分解层数和阈值选择方法，需要进行大量的对比仿真实验以找到最合适的方法，这样做费时费力，有时候还得不到合适的结果。大部分学者一般会根据自己的使用经验来选取各个参数，这难免会造成信号降噪效果不佳的状况。

1.2FastICA信号处理方法

独立分量分析(independent component analysis，ICA)方法是盲源分离中最常用的处理方法，它是一种从多个线性混合信号中分离出源信号的方法。线性混合信号分离过程中，可通过对分离结果的非高斯性度量来表示分离结果间的相互独立性，当非高斯性度量达到最大时，则表明已完成对各独立分量的分离，即当信号中各个成分间存在很强独立性时，分离结果对源信号可达到很好的估计效果[7]。

ICA模型可以简单描述为：设有n个独立的源信号U(t)=[U1(t)U2(t) …Un(t)]T，m个观测信号G(t)=[G1(t)G2(t) …Gm(t)]T，单路信号可表示为Gi(t)=si1U1(t)+si2U2(t)+…+sinUn(t),i=1,2,…,m,其矩阵表达形式为

(2)

G(t)=SU(t)

(3)

其中，S为m×n阶未知混合矩阵。ICA的根本问题在于：在混合矩阵S和源信号U(t)完全未知的情况下，需利用源信号先验知识，通过线性变换来实现盲信号分离。

ICA方法的使用基于以下假设条件[8]：①各个源信号之间相互统计独立，且最多只有一个为高斯分布；②观测信号的数目应该不小于源信号数目，即m≥n；③混合矩阵应该是广义可逆的。

由式(3)可知，如果能找到混合矩阵S的可逆矩阵V，即V=S-1，那么在观测信号G(t)已知的情况下，就可以估计出源信号：

(4)

考虑到系统消耗与速度问题，本文实际算法过程中采用了基于负熵的FastICA方法。

FastICA算法学习规则是寻找解决混合矩阵W使WTG(Y=WTG)具有最大非高斯性，可利用下式得出的负熵Ng(Y)的近似值来度量：

Ng(Y)={E[g(Y)]-E[g(YG)]}2

(5)式中，YG为与Y具有相同方差的高斯随机变量;E[·]为均值运算;g(·)为非线性函数，可取g(·)=tanh(a1y),取a1=1。

FastICA算法如下：首先,WTG的负熵最大近似值能通过对E[g(WTX)]进行优化来获得。根据Kuhn-Tucker条件，在E[g2(WTX)]=‖W‖2=1的约束下，E[g(WTX)]最优值能在满足下式的点上获得：

E[Gg(WTG)]+βW=0

(6)

(7)

式中，g′(·)为g(·)的导数。

在实际运用时，FastICA算法中的期望用它们的估计值来代替。

实际上，在运用FastICA算法时，必须满足ICA方法的3个使用假设条件，所以在解决观测信号数目不足等欠定问题时，FastICA无法准确分离出各个变量，这时候就需要与其他方法结合使用，来弥补自身算法的缺陷。本文将小波降噪算法和FastICA算法相结合来共同完成轴承振动信号的降噪处理。

1.3小波-FastICA联合降噪方法

小波分析对原始振动信号的处理结果和原始信号一起构成FastICA的输入矩阵，可以有效地弥补ICA只能应用于观测信号源数不少于信号源数的超定盲源分离的缺点，解决单通道ICA的欠定问题。因为原始振动信号已经进行过小波分析，所以可以有效地解决由于引入虚拟振动信号不当而造成的分离效果差的问题，从而提高FastICA的分离效率和分离精度。

小波-FastICA方法具体实现步骤如下：

(1)利用选定的小波阈值、阈值规则以及分解层数对原始信号进行小波去噪处理，得到处理后的振动信号；

(2)将原始振动信号和小波处理后的信号作为盲源分离输入矩阵，利用FastICA算法对原始信号进行分离，实现原始信号降噪的目的；

(3)分析降噪后信号的峭度值，比较小波和小波-FastICA降噪效果的优劣。

2 仿真信号降噪分析

2.1仿真信号的构建

构建仿真信号表示轴承故障含噪信号：

(8)

其中，轴承的固有频率fn=3 kHz，ωn=1/fn,位移y0=5 m/s2，阻尼系数δ=0.1，冲击故障发生的周期为0.01 s，采样频率fs=20 kHz,采样点数N=4096。用MATLAB软件中的wgn()函数给轴承故障仿真信号加入高斯噪声信号，加噪信号时域图见图1。

图1 轴承仿真振动信号时域图Fig.1 Time domain diagram of bearing simulation vibration signal

从轴承仿真振动信号时域图分析可知，该信号中含有较大的噪声信号，对故障特征的提取造成较大的干扰，因此后续降噪处理就尤其重要。

2.2仿真信号的处理

在对仿真信号进行小波降噪处理时，根据1.1节关于小波阈值选取规则的分析，首先根据表1的各种组合对仿真信号进行降噪处理。据表1可以得到384种小波降噪方法，分别对这些方法进行验算，发现使用rigrsure，选取软阈值，阈值尺度改变比例为sln，小波分解层数为5，小波基为sym6时，轴承仿真故障含噪信号降噪处理效果更加明显，如图2所示。将图2得到的小波处理降噪信号yd(t)，与原始信号y(t)组成FastICA分析的输入矩阵Z(t)(Z(t)=[y(t);yd(t)])，解决ICA分析的欠定问题，随后对输入矩阵Z(t)进行FastICA独立分量分析，得到图3所示的降噪信号时域图。

表1 小波降噪函数组合Tab.1 The combination of wavelet denoising function

图2 仿真信号小波降噪时域图Fig.2 Time domain diagram of simulation signal wavelet denoising

图3 仿真信号小波-FastICA降噪时域图Fig.3 Time domain diagram of simulation signal wavelet-FastICA denoising

2.3降噪性能的分析

峭度指标是量纲一参数，且它与轴承转速、尺寸、载荷等无关，对冲击信号特别敏感，特别适用于表面损伤类故障诊断。在轴承无故障运转时，由于各种不确定因素的影响，振动信号的幅值分布接近正态分布，峭度指标值K≈3;随着故障的出现和发展，振动信号中大幅值出现的概率密度增大，信号幅值的分布偏离正态分布，正态曲线出现偏斜或分散，峭度值也随之增大。峭度指标的绝对值越大，说明轴承越偏离其正常状态，故障越严重，当K>8时，则很可能出现了较大的故障[9]。对原始信号、小波降噪信号以及小波-FastICA降噪信号进行信号峭度值计算：

(9)

计算三种信号的峭度值分别为3.4267、8.0863、9.8562。可得三种仿真信号的峭度值逐渐增大，表明本文方法对信号的降噪取得预期效果，且对比分析图1～图3发现，仿真信号降噪效果明显，信号的故障冲击变得更加清晰，可以比较清楚地看出轴承有明显的故障。本文方法在轴承仿真故障振动信号降噪中可行，后续将用该方法对实际实验数据进行分析。

3 滚动轴承振动信号降噪分析

本文采用的滚动轴承振动信号实验数据来源于美国凯斯西储大学电气工程实验室的滚动轴承故障模拟实验台的轴承数据,滚动轴承故障模拟实验台如图4所示。

图4 滚动轴承故障模拟实验台Fig.4 Rolling bearing fault simulation experiment rig

该实验台主要由一个负载为2.33 kW的电动机、一个扭矩传感器和编码器、一个测试计，以及电子控制系统组成。实验中使用加速度传感器采集振动信号，通过使用磁性底座将传感器安放在电机壳体上。对于实验台滚动轴承，分别在内圈和外圈采用电火花加工的单点损伤法来获得轴承的局部损伤，损伤直径范围为0.18～0.71 mm，其中轴承外圈损伤点的位置相对于加载载荷方向为时钟3点钟、6点钟、12点钟3个不同位置，在0～2237.1 W(0～3马力)电机负载恒速(1720～1797 r/min)状态下运转，在驱动端轴承和风端轴承外壳垂直方向上测量加速度值[10]。

在1491.4 W(2马力)载荷情况下，截取驱动端轴承深沟球轴承SKF6205-2RS JEM故障信号作为实验数据。该轴承的结构尺寸如下：滚动体直径8.182 mm，内圈直径25.001 mm，接触角0°，外圈直径51.999 mm，滚动体数目为9。

故障原始振动信号分别为内圈故障、外圈故障(损伤点在3点钟方向,损伤直径0.21 mm)和正常振动原始数据，其数据长度均为6000，采样频率为12 kHz，可分别得到驱动端轴承三种原始振动信号时域图，如图5～图7所示。

图5 内圈故障原始振动信号时域图Fig.5 Time domain diagram of inner ring fault original vibration signal

图6 外圈故障原始振动信号时域图Fig.6 Time domain diagram of outer ring fault original vibration signal

图7 正常原始振动信号时域图Fig.7 Time domain diagram of normal original vibration signal

由驱动端轴承原始振动信号时域图可知，轴承内圈和外圈加速度有突变情况且具有一定的规律性，正常振动数据相对平滑，且该原始信号中存在大量的噪声信号。针对原始信号包含噪声较多的情况，采用本文所研究的方法进行信号去噪处理。

首先根据小波参数进行原始信号降噪处理，得到处理后的信号时域波形,如图8～图10所示;然后利用基于小波处理的FastICA去噪分析方法，得到如图11～图13所示的小波-FastICA联合降噪时域图。

图8 内圈故障振动信号小波降噪时域图Fig.8 Time domain diagram of inner ring fault vibration signals wavelet denoising

图9 外圈故障振动信号小波降噪时域图Fig.9 Time domain diagram of outer ring fault vibration signal wavelet denoising

图10 正常振动信号小波降噪时域图Fig.10 Time domain diagram of normal vibration signal wavelet denoising

图11 内圈振动信号小波-FastICA联合降噪时域图Fig.11 Time domain diagram of inner ring vibration signal wavelet-FastICA denoising

图12 外圈振动信号小波-FastICA联合降噪时域图Fig.12 Time domain diagram of outer ring vibration signal wavelet-FastICA denoising

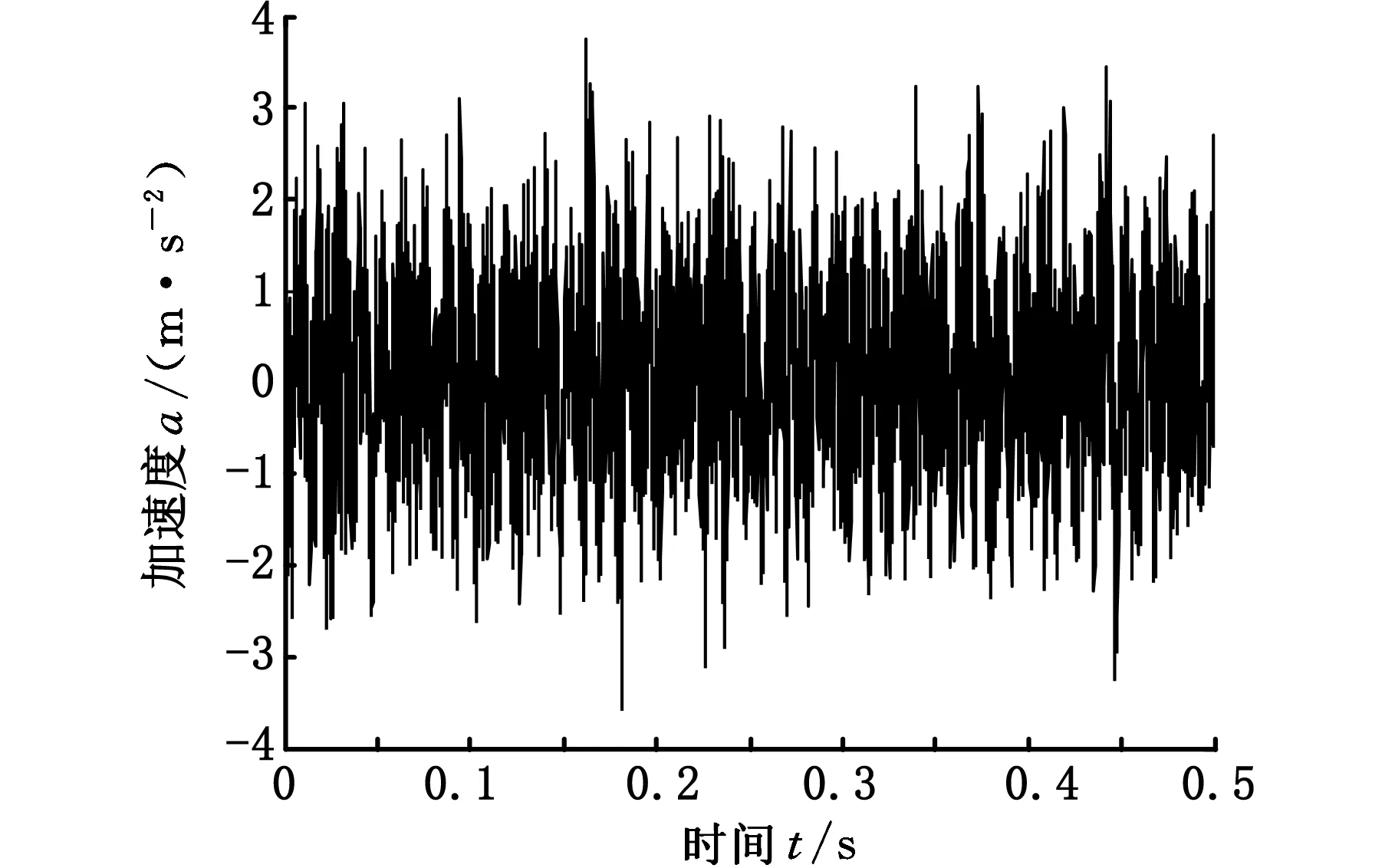
图13 正常振动信号小波-FastICA联合降噪时域图Fig.13 Time domain diagram of normal vibration signal wavelet-FastICA denoising

将图5、图8和图11时域图作为第一组，图6、图9和图12作为第二组，图7、图10、图13作为第三组，分别对每一组时域图进行对比分析，可知采用小波-FastICA联合降噪方法时，内外圈轴承振动故障信号冲击更加明显，而对于正常振动信号，时域信号振动规律性更加明显，符合正常信号振动规律。分别计算滚动轴承振动的原始信号、小波去噪信号以及小波-FastICA联合降噪信号的峭度值，结果如表2所示。

分析表2各峭度值可发现，对于正常信号，其峭度值均小于3，表明无故障特征，随着信号经过降噪处理，峭度值逐渐增大(依然小于3)，表明噪声信号得到有效去除；对于外圈信号，峭度值均在8附近，表明已经存在明显的故障特征；对于内圈信号，峭度值明显大于外圈故障信号峭度值，表明内圈故障比外圈故障严重；而经过去噪处理以后，三种信号的峭度值均有明显增大，表明滚动轴承振动信号所含噪声得到有效地去除，达到去噪效果。

表2 滚动轴承振动信号峭度值Tab.2 Kurtosis value of vibration signal ofrolling bearings

4 结语

本文通过MATLAB对滚动轴承故障振动信号进行仿真，采用小波对原始信号进行处理，将其处理结果与原始信号一起构建二维输入矩阵，输入到FastICA方法中进行分离，有效地解决了盲源分离中源信号数目欠定问题，最终使原始振动信号得到理想的降噪效果。该方法在实际滚动轴承故障振动信号去噪中的成功应用，表明该方法适于分析工程实践中轴承等振动信号，基于小波-FastICA的联合降噪方法计算步骤简单，原始信号经过该方法处理后，噪声得到一定程度的滤除。

[1] 高萍,祖静.基于MATLAB的小波去噪技术浅析[J].科技信息(学术研究),2006,12(11):45-48. GAO Ping,ZU Jing. The Elementary Analysis of Wavelet Denoising Technology Based on MATLAB[J]. Science and Technology Information (Academic Research),2006,12(11):45-48.

[2] 王楠,杜劲松.小波消噪在振动信号处理中的应用[J].仪器仪表学报,2001,22(4):225-226. WANG Nan,DU Jinsong. Application of Wavelet De-noising in Vibration Signal Processing[J]. Chinese Journal of Scientific Instrument,2001,22(4):225-226.

[3] 钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J].振动,测试与诊断,2011,31(4):459-463． QIAN Zhengwen, CHENG Li, LI Yinghong. Noise Reduction Based on Singular Value Decomposition[J].Journal of Vibration, Measurement & Diagnosis，2011,31(4):459-463.

[4] 沈路,周晓军,张文斌,等.广义数学形态滤波器的旋转机械振动信号降噪[J].振动与冲击,2009,28(9):70-73. SHEN Lu,ZHOU Xiaojun,ZHANG Wenbin,et al.De-noise for Vibration Signals of a Rotating Machinery Basedon Generalized Mathematical Morphological Filter[J].Journal of Vibration and Shock,2009,28(9):70-73.

[5] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005. SUN Yankui. Wavelet Analysis and Application[M].Beijing:China Machine Press,2005.

[6] 孔玲军.MATLAB小波分析超级学习手册[M].北京:人民邮电出版社,2014. KONG Lingjun. MATLAB Wavelet Analysis Super Learning Manual[M].Beijing:Post & Telecom Press,2014.

[7] GUO Yu,WU Xing,NA Jing,et al. Simultaneous Faults Identification of Rolling Element Bearings and Gears by Combining Kurtogram and Independent Component Analysis[J].Journal of Vibroengineering,2015,17(3):1341-1350.

[8] 郭卫,李好.独立分量分析(ICA)在齿轮箱故障诊断系统中的应用[J]. 组合机床与自动化加工技术,2009(2):74-80. GUO Wei, LI Hao. The Application of Independent Component Analysis(ICA) in the Fault Diagnosis System of Gear Case[J].Modular Machine Tool & Automatic Manufacturing Technique,2009(2):74-80.

[9] 袁云龙.基于峭度-小波包分析的滚动轴承故障诊断[J].新技术新工艺,2008(5):43-46. YUAN Yunlong.Fault Diagnosis of Rolling Bearing Based on Kurtosis-wavelet Packet Analysis[J].New Technology & New Process,2008(5):43-46.

[10] SMITH W A, RANDALL R B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: a Benchmark Study[J]. Mechanical Systems and Signal Processing，2015,64/65:100-131.

(编辑袁兴玲)

ApplicationResearchofFastICANoiseReductionMethodBasedonWaveletAnalysisinFaultDiagnosisofRollingBearing

WU Yapeng WANG Jifang XU Xiaoli JIANG Zhanglei

Beijing Information Science and Technology University,the Ministry of Education Key Laboratory of Modern Measurement and Control Technology, Beijing,100192

There is a problem of depending on experience of selecting parameters when wavelet analysis method is used to make noise reductions of vibration signals. And there is a problem of undetermined parameters when ICA method is used to make noise reduction of vibration signal. In order to avoid disadvantages of wavelet denoising and ICA method when they were used respectively. A method of wavelet denoising and FastICA independent component analysis based on negative entropy was proposed to deal with the noise signal of rolling bearings. Firstly, original signals were processed by wavelet denoising. Then the processing results were combined with the original signal to form input matrix of FastICA, and the FastICA noise reduction processes were performed. Finally, the effectiveness of the method was verified by vibration signal of rolling bearings. Experimental analysises show that this method improved the kurtosis of vibration signals and the purposes of noise reductions of vibrartion signals of rolling bearings was achieved.

wavelet analysis; independent component analisis(ICA); noise reduction; rolling bearing

2016-12-19

国家高技术研究发展计划(863计划)资助项目(2015AA043702)；北京市教委科研计划资助项目(KM201611232020)

TH212；TH213.3

10.3969/j.issn.1004-132X.2017.18.006

吴雅朋，男，1992年生。北京信息科技大学现代测控技术教育部重点实验室硕士研究生。研究方向为机电设备状态监测与故障诊断技术。王吉芳，女，1963年生。北京信息科技大学现代测控技术教育部重点实验室教授、博士。徐小力，男，1951年生。北京信息科技大学现代测控技术教育部重点实验室主任、教授、博士研究生导师。蒋章雷，男，1983年生。北京信息科技大学现代测控技术教育部重点实验室助理研究员、博士。