滚动轴承性能不确定性与可靠性评估

常 振 夏新涛,2 李云飞 刘红彬

1.河南科技大学机电工程学院，洛阳，4710032.河南科技大学机械装备先进制造河南省协同创新中心，洛阳，471003

滚动轴承性能不确定性与可靠性评估

常 振1夏新涛1,2李云飞1刘红彬1

1.河南科技大学机电工程学院，洛阳，4710032.河南科技大学机械装备先进制造河南省协同创新中心，洛阳，471003

以灰色系统理论和泊松计数过程为基础，对滚动轴承性能不确定性进行参数量化，并在设定阈值条件下研究不同工况下轴承性能可靠性，进而建立其性能不确定性与可靠性匹配序列，以寻找轴承服役期间两者之间的内在联系。根据轴承运转期间某属性时间序列，进行灰自助处理得到该属性的不确定性；然后参考设定阈值进行泊松计数，获得该时间序列的有效变异强度，进而得到其性能运转可靠性；最后分析不确定性与可靠性两者之间的灰关系。实验结果显示，滚动轴承性能不确定性与可靠性的演变状况可以被真实描述，两者归一化处理结果十分相像，有着明显的灰关系，各案例的实验结果保持良好的一致性。

滚动轴承；不确定性；可靠性；灰关系

0 引言

滚动轴承保持最低的不确定性及最高的可靠性，是主机系统实现最佳精度态势运行的基础。滚动轴承服役期间其性能时间序列包含不断变化的性能不确定性与可靠性轨迹的大量变异信息，可据此作出某些方面的评估与预报并及时对机械设备作出维护与诊断，避免不必要的损失[1-2]。

轴承运转期间,性能时间序列区间波动或间歇有着明显的不确定性，对轴承工作精度、平稳性、生产质量的影响随渗透率的增大而愈发突出；若不确定性增至一定程度，则会伴有产品失效概率与安全隐患的增加，其产品可靠性将逐渐下降。另外，产品能否在规定条件、规定时间内完成规定的功能，其可靠性起着至关重要的作用；并且，在可靠性变化时，产品性能不确定性可能早已显现出潜在的变化迹象。然而，性能不确定性与可靠性两者之间是否有联系及其关联程度的大小，国内外尚未有研究。本文基于灰关系[3-4]进行两属性系统关联性分析，这类研究通常依赖于已知分布与趋势等先验信息的传统统计学理论，而研究伴有非稳定性、非线性演变特征的滚动轴承振动、摩擦力矩等时间序列问题仍有困难[5-8]。

关于不确定性与可靠性方面的评估，以及基于灰关系的实际应用问题，人们进行了很多研究并取得了相应的成果。孙强等[9]根据不确定性属性特点，将不确定性分为四类：随机性、模糊性、灰性及混合不确定性，并分析了各类方法的研究现状与不足。KAUSCHINGER等[10]用经典Palmgren分析模型研究摩擦力矩分布特征，并得出滚动轴承摩擦力矩有着十分明显的不确定性。刘志成等[11]基于区间优化方法，构建出电焊结构疲劳寿命不确定性的分析模型。XIA等[12-13]基于乏信息系统理论，用灰自助法描述了滚动轴承摩擦力矩不确定性信息，并融合模糊集合理论和混沌原理，用模糊混沌法评估滚动轴承性能时间序列的非线性演变过程，进而挖掘其失效隐患。高攀东等[14]、朱德馨等[15]基于航空、高铁轴承小样本无失效数据，采用贝叶斯多层估计法建立可靠性寿命评估模型。GRASSO等[16]、ALI等[17]、KATSIFARAKIS等[18]提出数据驱动法来强化分析滚动轴承的故障振动信号，并根据滚动轴承运转期间实时测量的非线性的振动信号，实现了轴承的状态监测和故障诊断。SEHGAL等[19]和LI等[20]考虑各轴承组件之间的相互作用关系，提出了基于状态空间模型的可靠性预测方法，进而监测退化参数的概率密度分布演变信息及未来状态下可靠度的大小。刘英等[21]融合多个可靠性影响因素，并结合专家经验以及已知信息，提出一种基于区间灰色系统理论的可靠性综合评估方法。PANDA等[22]和KUMAR等[23]通过灰色关联分析，对加工制造过程进行参数优化和多响应问题处理。

本文根据轴承服役期间振动及摩擦力矩的性能时间序列，借助灰色系统理论和泊松计数过程，进行滚动轴承性能不确定性及其可靠性评估。

1 建立模型

1.1滚动轴承性能不确定性分析

轴承运转期间，某性能参数记录仪在设定时间间隔下采样一次，可得到性能时间序列，用向量X表示为

X=(x(1),x(2),…,x(t),…,x(T))

(1)

式中，X为滚动轴承性能信号原始数据；x(t)为X中的第t个数据，t=1, 2,…,T，其中T为X中的数据个数。

为满足灰预报模型GM(1,1)[24]关于x(t)≥0的要求，在式(1)中，若有x(t)<0，则人为地选取一个常数c，使得x(t)+c≥0。在实际分析时，X表示为

X=(x(1)+c,x(2)+c,…，x(T)+c)

(2)

从X中取与时刻t紧邻的前m个时刻的数据(包括时刻t的数据)，构成时刻t的动态分析子向量：

Xm=(xm(t-m+1)，xm(t-m+2)，…，xm(t))

(3)

t≥m

运用自助法[24]，在时刻t，从Xm中等概率可放回地随机抽取一个数，共抽取m次，可得到一个自助样本Y1，它有m个数据。按此方法重复执行B次，得到B个样本，可表示为

YBootstrap=(Y1,Y2,…,Yb,…,YB)

(4)

式中，Yb为第b(b=1,2,…,B)个自助样本；B为自助再抽样总次数，即自助样本的个数。

有

Yb=(yb(t-m+1),yb(t-m+2)，…,yb(t))

(5)

b= 1,2,…,B

根据灰预报模型GM(1,1)，设Yb的一次累加生成向量表示为

Xb=(xb(t-m+1),xb(t-m+2)，…，xb(t))

(6)

u=t-m+1,t-m+2,…,t

灰生成模型可以描述为如下的灰微分方程：

(7)

式中，c1、c2为待定系数。

用增量代替微分，表示为

(8)

式中,Δu取单位时间间隔1。

再设均值生成序列向量为

Zb=(zb(t-m+1),zb(t-m+2),…,zb(t))

(9)

zb(u)=0.5xb(u)+0.5xb(u-1)

在初始条件xb(t-m+1)=yb(t-m+1)下，灰微分方程的最小二乘解为

(10)

其中待定系数c1和c2表示为

(c1,c2)T=(DTD)-1DT(Yb)T

(11)

且有

D=(-Zb,I)T

(12)

I=(1,1，…,1)

(13)

然后由累减生成，可得到ω=t+1时刻的预测值

(14)

因此，在ω=t+1时刻，有B个数据，可表示为如下向量：

(15)

ω=t+1

由于B很大，根据式(15)可建立当前时刻关于属性xm的概率密度函数

fω=fω(xm)

(16)

其中，fω又叫作灰自助概率密度函数，描述轴承性能信号ω时刻的瞬时状态。

式(16)中，该瞬时状态信息包含有两个参数：t时刻的估计真值、估计区间。估计真值可表示为

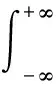
(17)

对于离散变量，式(17)可表示为

(18)

式中，X0为估计真值；L是数据组数(fω被分为L组)；l表示第l组，l=1,2,…,L；xml为第l组数据中的值；Fω(xml)为点xml的灰自助概率。

设显著性水平为α∈[0,1]，则置信水平为

P=(1-α)×100%

(19)

在t时刻，置信水平为P时，真值的估计区间为

[XL,XU]=[XL(ω),XU(ω)]=[Xα/2,X1-α/2]

(20)

式中，Xα/2为对应概率是α/2的参数值xm；X1-α/2为对应概率是1-α/2的参数值xm；XL为区间下边界，XU为区间上边界。

在t时刻的区间波动范围表示为

U=U(ω)=XU-XL

(21)

式中，U为估计不确定度，即在t时刻、置信水平为P时的瞬时不确定度。

评估过程中，假设总共有t=T个数据，如果有h个数据在估计区间[XL,XU]之外，则评估结果的可靠度可表示为

PR=[1-h/(T-m)]×100%

(22)

其中，PR表示用灰自助法进行预报评估的可靠程度。一般PR不等于置信水平P；由PR的定义可知，PR越大，不确定性的评估结果越好；在统计学与实践中，最好PR>P。

通常，置信水平P越大，在ω时刻的区间不确定性U越大。若P=100%，则U取得最大，结果最可信。但U越大，估计区间[XL,XU]越偏离真值，估计结果越失真，因此，定义

(23)

式中，Umean为动态平均不确定性。

考虑到最小不确定性，置信水平P应满足

fmin=min(Umean)

(24)

评估参数Umean是一个统计量，可作为随机波动状态不确定性的评价指标[25]。实际分析中，滚动轴承性能不确定性用Umean来表达，也可称为动态平均不确定性。根据式(23)和条件式(24)，最理想且可靠的评估结果是在PR=100%条件下，Umean为最小，即满足条件式(24)。

1.2滚动轴承性能可靠性原理

1.2.1计数过程

假设在滚动轴承某性能信号的时间序列X(式(1))中有s个数据越过性能阈值v，即落在区间[-v,v]之外，则X的变异强度θ表示为

(25)

1.2.2可靠性评估

任何计数过程均可用泊松过程描述：

(26)

式中，τ为单位时间，τ=1,2,…；n为失效事件发生的次数，n=0,1,…，即工作性能恶劣可能已造成轴承失效；Q为失效事件发生n次的概率。

由泊松过程可以获得事件发生的可靠度R。

在滚动轴承性能可靠度求取时n=0，即产品未发生失效前的概率；τ=1时为当前时间滚动轴承性能可靠度，即当前时间序列X的性能可靠度。根据式(26)可靠度表示为

R(θ)=exp(-θ)

(27)

则性能时间序列X的可靠度只是关于变异强度θ的函数，θ可由式(25)求得。在具体实施时，若可靠度不小于90%，则认为轴承性能是可靠的；否则不可靠。

1.3不确定性及可靠性的灰关系评估

1.3.1不确定性及可靠性矢量

根据式(23)、式(24)可求出每组性能时间序列的不确定性Umean，构成不确定性矢量Φ1，即

Φ1=(φ1(1)，φ1(2),…,φ1(n),…,φ1(N))

(28)

式中，φ1(n)为Φ1中的第n个数据，n=1,2,…,N，即Umean1,Umean2,…,UmeanN。

同样，根据式(27)可求出每组性能时间序列的可靠性R，构成可靠性矢量Φ2，即

Φ2=(φ2(1)，φ2(2),…,φ2(n),…,φ2(N))

(29)

式中，φ2(n)为Φ2中的第n个数据，n=1,2,…,N，即R1,R2,…,RN。

基于灰关系概念，对这两个数据序列之间的性能属性进行灰分析，可以有效监测滚动轴承性能不确定性及可靠性之间的关系。

1.3.2两个序列的灰关系分析

经典集合论的特征函数是基于二值逻辑0(假)与1(真)的，即系统之间的关系非真即假，不存在第三种情况;而工程应用中系统属性大都处于从真到假或从假至真变化的过渡状态。邓聚龙[24]基于灰色系统理论提出灰关系概念，用于解决内涵模糊而边界清晰的系统属性之间的相对关系。本文利用灰关系建立滚动轴承性能不确定性与可靠性之间的联系，然后结合灰置信水平分析两者之间的关联程度。

式(28)、式(29)中，Φ1和Φ2的样本分别为φ1(n)和φ2(n)，设

(30)

(31)

归一化处理得

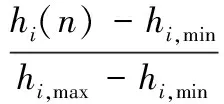
(32)

则有

Gi=(gi(n))

(33)

n=1,2,…,Ni∈(1,2)

式中，Gi为Φi的规范化生成序列。

对于归一化生成序列Gi，有

gi(n)∈[0,1]gi(1)=0gi(N)=1

(34)

在最少量信息原理下，对于任意的n=1,2,…,N，若Gi是规范化排序序列，则参考序列GΩ的元素可以是常数0，即

gΩ(n)=gΩ(N)=gΩ(1)=0

(35)

取分辨系数ε∈(0,1]，可得到灰关联系数的表达式

(36)

n=1,2,…,N

其中，ΔΩi(n)为灰差异信息，表示为

ΔΩi(n)=|gi(n)-gΩ(n)|

(37)

定义灰关联度为

(38)

定义两个排序序列Φ1和Φ2之间的灰差为

d1,2=|γΩ1-γΩ2|

(39)

根据灰差d1,2可得到序列Φ1和Φ2之间的基于灰关联度的相似系数r1,2，简称灰相似系数，表示为

r1,2=1-d1,2

(40)

则有

(41)

式中，V为灰相似矩阵，又称为灰关系属性，简称灰关系，且有0≤r1,2≤1。

给定Φ1和Φ2，对于ε∈(0,1]，总存在唯一的一个实数dmax=d1,2max，使得d1,2≤dmax，称dmax为最大灰差，相应的ε称为基于最大灰差的最优分辨系数。

定义基于两个数据序列Φ1和Φ2之间灰关系的属性权重为

(42)

式中，属性权重f1,2∈[0,1]，参数η∈[0,1]。

1.3.3灰置信水平求取

根据灰色系统的白化原理与对称原理，在给定准则下，默认λ为真元的代表。对于式(42)，给定Φ1和Φ2，取参数λ∈[0,1]为水平，若存在一个映射f1,2≥λ，则认为Φ1和Φ2具有相同的属性，即λ为研究对象从一个极端属性过渡到另一极端属性的边界，也叫模糊数。当λ=0.5时，研究对象的两实体模糊性达到最大，介于较难分辨的真和假之间；当λ>0.5时，Φ1和Φ2灰关系趋于清晰；当λ<0.5时，两事物关联度较小或两者之间差异大，所以取f0i=λ=0.5，认为不确定性序列Φ1和可靠性序列Φ2具有相同的属性。

设η∈[0,0.5]，由式(42)可得

dmax=(1-f1,2)η

(43)

令

P1,2=1-(1-λ)η=(1-0.5η)×100%

(44)

其中，P1，2为灰置信水平，又称为灰理论概率；P1,2描述了Φ1和Φ2属性相同的可信度；η值可由式(43)求得。灰置信水平取值越大，表明滚动轴承性能时间序列所对应的性能不确定性Φ1和可靠性Φ2之间的关系越紧密；反之，两者之间的关系越疏松。这表明轴承性能不确定性和可靠性两个不同属性之间的本质关系。具体实施时，可取f1,2=0.5，通过计算灰置信水平来评估两者关联程度。若灰置信水平不小于90%，则认为轴承性能不确定性与可靠性两者之间关系十分紧密；否则不紧密。

2 案例分析

2.1美国CaseWesternReserveUniversity的轴承振动时间序列(案例1)

该案例为轴承内沟道表面磨损引起振动加速度演变的仿真案例，数据来自美国Case Western Reserve University的轴承数据中心网站。待检测的轴承支撑着电动机的转轴，且驱动端轴承型号为SKF6205，用加速度传感器测量轴承振动加速度信号，轴承运转速度为1797 r/min，采样频率为12 kHz，采样后可得到轴承内圈沟道有损伤的故障数据，损伤直径分别为0 mm、0.1778 mm、0.5334 mm、0.7112 mm。所得轴承振动加速度的原始数据序列X如图1所示。

(a)振动序列X1(磨损直径为0 )

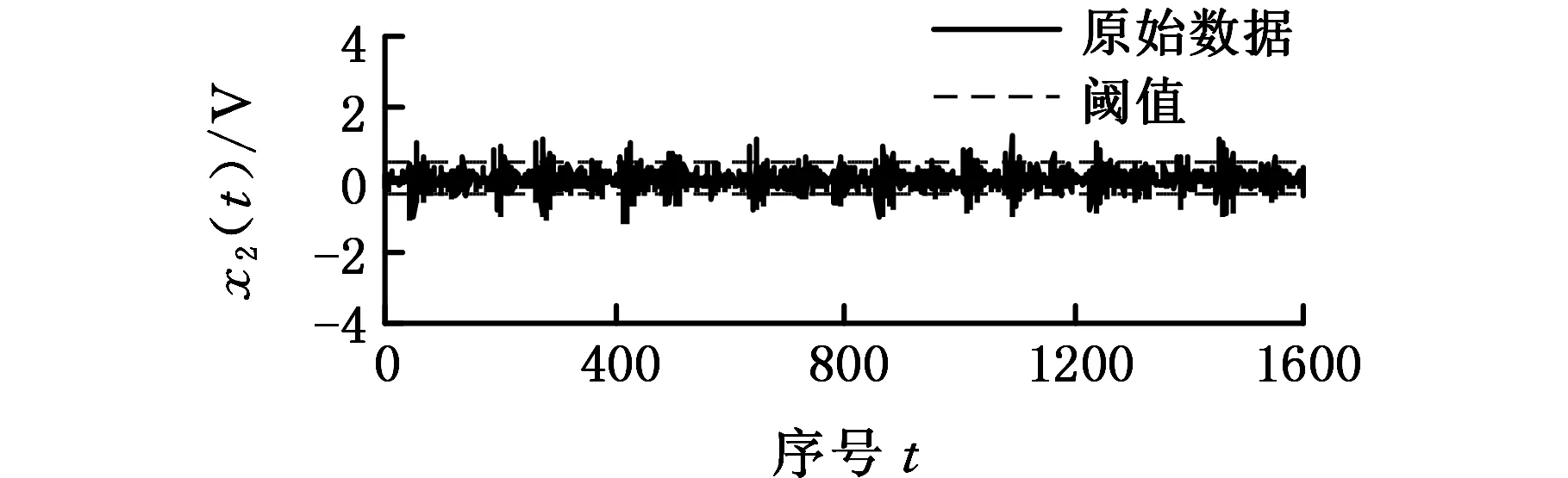
(b)振动序列X2(磨损直径为0.1778 mm)

(c)振动序列X3(磨损直径为0.5334 mm)

(d)振动序列X4(磨损直径为0.7112 mm)图1 轴承在不同磨损直径下的振动信号Fig. 1 Bearing vibration signals under different fault diameters

图1中的虚线为阈值c。由图1可知，随着磨损直径的增大，轴承振动状况愈加剧烈，区间波动越大；且超过阈值的时间个数越多，则变异强度会明显增加，进而失效概率会增大。

对时间序列X1、X2、X3、X4分别用灰自助法处理，在建立评估模型时，取自助评估因子m=5、自助再抽样次数B=1000、置信水平P=100%，根据式(1)～式(5)得到自助样本YBootstrap，由式(6)～式(20)求出下一时刻的估计真值X0、估计区间[XL,XU]，再根据式(21)～式(24)求出不同磨损直径下轴承振动性能不确定性Umean，结果见表1。

表1 轴承振动性能不确定性Umean和可靠性R(案例1)

分别对时间序列X1、X2、X3、X4设定阈值、计数处理，具体分析时取阈值c=0.4 V，即计算出原始数据超出±c的次数。由式(25)得到不同磨损直径下振动信号的变异强度，再由式(27)得到不同磨损直径下轴承振动性能可靠性R，结果见表1。

由表1可以看出，轴承振动性能不确定性Umean随磨损直径的增大而增大，但这种增大关系是非线性的。由计数过程得到超出阈值的次数s，同样s随磨损直径的增大而增加，因此变异强度逐渐增大，且这种增大关系也是非线性的。轴承振动性能可靠性随磨损直径的增大而逐渐下降，磨损直径为0.1778 mm、0.5334 mm、0.7112 mm时，其可靠性均小于90%，说明轴承恶性变异严重、性能不可靠且变化趋势与实际情况符合。由此说明不确定性的非线性增加会伴有可靠性的降低，两者之间存在负相关关系，但要判断这种关联程度的强弱，或实现两者之间的统一评价，就要利用灰关系理论。

轴承振动性能不确定性与其可靠性之间进行灰关系分析时，取参数f1,2=0.5，由表1可知两者之间为负相关，在计算时为使两者极性统一，应将其中一属性人为地添加负号，即得到两个矢量序列Φ1=(-0.2369, -1.5048, -2.3982, -4.4753)、Φ2=(1.00, 0.8759, 0.7334, 0.5485)，由式(30)～式(34)，可对两序列归一化处理，得到规范化生成序列G1和G2，结果如图2所示。

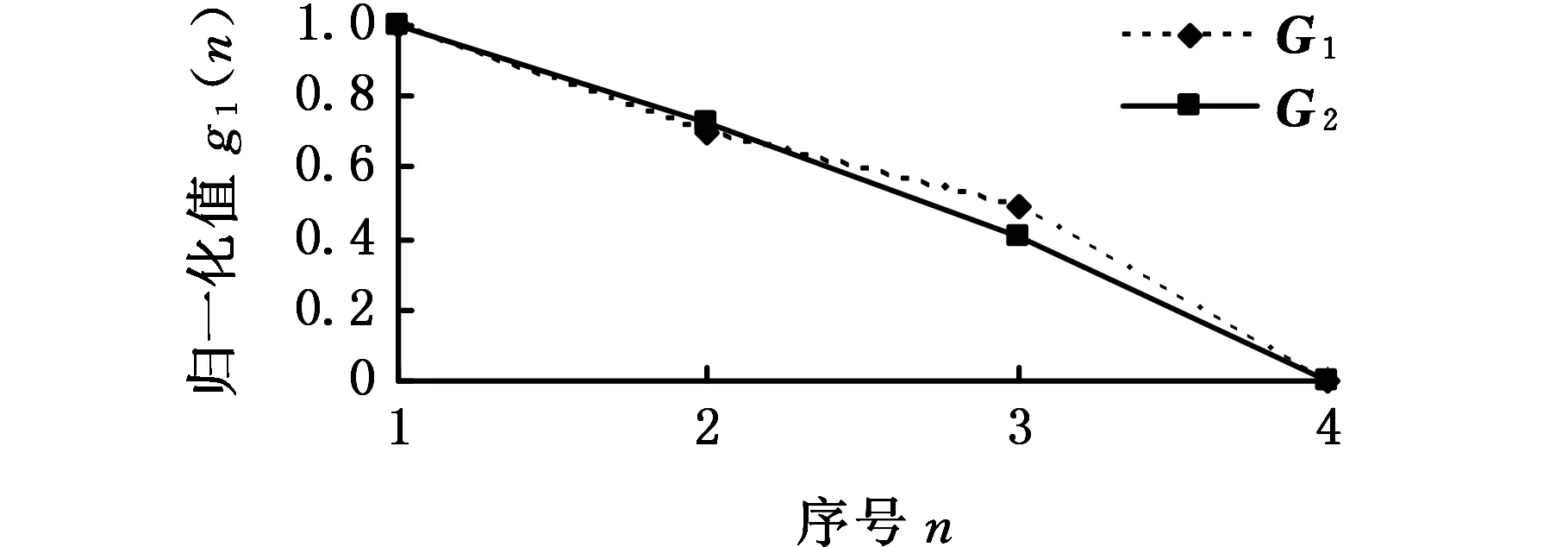
图2 Φ1和Φ2序列归一化处理结果(案例1)Fig. 2 Normalization processing results of seriesΦ1 and Φ2(case 1)

由图2可知，Φ1和Φ2两序列归一化处理后所得的规范化序列G1和G2十分相似，整体变化趋势一致，且几乎完全重合，这也说明了两序列关系紧密。为说明两序列关系紧密程度，在给定参数f1,2=0.5条件下，由式(35)～式(44)可求出两者之间的灰置信水平为99.08%≥90%，表明Φ1和Φ2两序列的关系紧密，说明轴承振动性能不确定性与其可靠性之间为负相关，有明显的灰关系，可信水平达到99.08%。该实验数据的分析结果有助于对滚动轴承振动特征进行研究。

2.2某机械装备的轴承振动加速时间序列(案例2)

该案例为监控滚动轴承振动性能随运转时间变化的案例，在监视某个机械装备运行期间，获得滚动轴承振动信号时间序列原始数据，如图3所示。由图3可知，随着轴承运转时间的延长，轴承振动状况愈加剧烈，区间波动越大，且超过阈值的次数越多。

图3 轴承振动信号时间序列矢量Fig. 3 Time series vector of bearing vibration signals

在建模分析之前，先对原始数据进行分组处理：将数据分为5组，每组400个，构成时间序列X1、X2、X3、X4、X5。建立评估模型时，取自助评估因子m=5，自助再抽样次数B=1000，置信水平P=100%，阈值c=0.35 V。同案例1，可求出不同时间段内轴承振动性能不确定性Umean和可靠性R，结果见表2。

表2 轴承振动性能不确定性Umean和可靠性R(案例2)

由表2可知，轴承振动性能不确定性Umean随运转时长的增加而增大，但这种增大关系同样是非线性的。由计数过程得到超出阈值的次数s，s随运转时长的增加而增加，因此变异强度逐渐增大，且这种增大关系也是非线性的。轴承振动性能可靠性随运转时长的增加而逐渐变小，时间序列X1、X2的可靠性均大于90%，表明轴承在时间段1～400、401～800之间工作性能可靠；时间序列X3、X4、X5的可靠性均小于90%，表明轴承在时间段801～1200、1201～1600、1601～2000之间工作性能不可靠。同样说明轴承不确定性的非线性增加会导致可靠性的降低，两者之间具有明显的负相关关系，根据灰关系理论可判定这种关联程度的强弱。

轴承振动性能不确定性与可靠性进行灰关系分析时，取参数f1,2=0.5，由表2可知两者为负相关。为使两者极性统一，在计算时将其中一属性添加负号，即得到两个矢量序列Φ1=(-0.5784, -0.6246, -1.5164, -2.3751, -4.5047)、Φ2=(1.00, 0.9753, 0.8187, 0.7012, 0.5798)，对两序列归一化处理，得到规范化生成序列G1和G2，结果如图4所示。

图4 Φ1和Φ2序列归一化处理结果(案例2)Fig.4 Normalization processing results of seriesΦ1 and Φ2(case 2)

由图4可知，Φ1和Φ2两序列归一化处理后所得的规范化序列G1和G2的整体变化趋势十分相似，但两者的重合程度不如案例1，即两者关系紧密程度不及案例1。为说明两序列的紧密程度，在给定参数f1,2=0.5条件下，求出两者之间的灰置信水平为95.27%≥90%，小于99.08%，所以Φ1和Φ2两序列的关联紧密，轴承振动性能不确定性与其可靠性之间为负相关关系，可信水平达到95.27%且小于案例1，验证了方法的准确性。该实验数据的分析结果显示，随着滚动轴承运转时间的延长，振动性能不确定性呈现出非线性增长趋势，可靠性呈现非线性降低趋势；且不确定性和可靠性之间存在明显的灰关系。

2.3轴承摩擦力矩时间序列(案例3)

该案例为大型滚动轴承摩擦力矩监测案例，且该大型轴承适用于较低转速工况。试验台由动力传动部件、转动盘部件、摩擦力传感器、应变仪、示波器等组成，测试过程中分别在3 r/min、7 r/min、12 r/min三种不同转速下完成，轴向载荷均为200 N。示波器采集数据样本，构成图5所示的摩擦力矩时间序列。

由图5可知，随着轴承转速的增大，摩擦力矩区间波动越大，且超过阈值的次数也越多。

由于原始数据分布不是在0 V上下波动，在建模分析之前，为准确得到阈值区间，先对原始数据求取均值，X01=0.0260 V，X02=0.0279 V，X03=0.0372 V。建立评估模型时，取自助评估因子m=5，自助再抽样次数B=1000，置信水平P=100%，阈值c=0.04 V，对应的阈值区间分别为(0.0260±0.04)V、(0.0279±0.04)V、(0.0372±0.04)V。同案例1、2，可求出不同时间段内轴承摩擦力矩性能不确定性Umean和可靠性R，结果见表3。

(a)时间序列X1(转速3 r/min)

(b)时间序列X2(转速7 r/min)

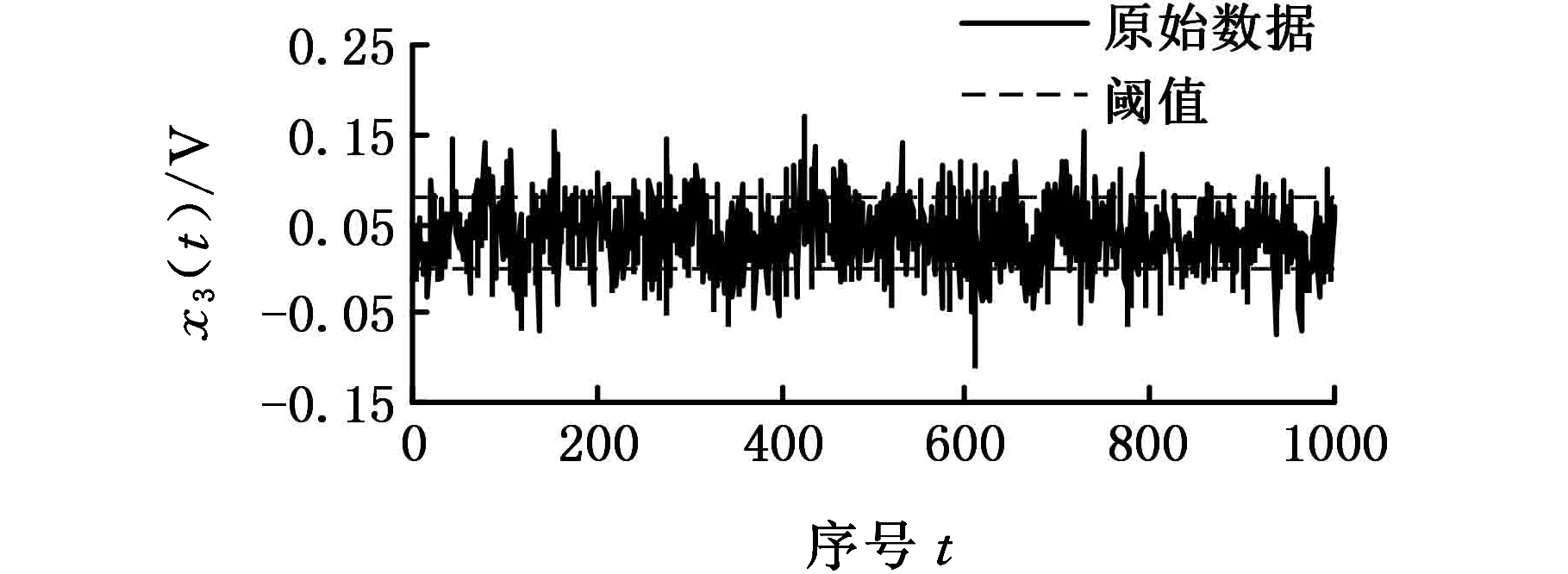
(c)时间序列X3(转速12 r/min)图5 轴承在不同转速下摩擦力矩信号Fig.5 Bearing friction torque signals under different rotational speeds

表3 轴承摩擦力矩不确定性Umean和可靠性R(案例3)

由表3可知，轴承摩擦力矩不确定性Umean随转速的增大而增大，但这种增大关系也是非线性的。由计数过程得到超出阈值的次数s，s同样随轴承转速的增大而增加，因此变异强度逐渐增大。轴承摩擦力矩性能可靠性随转速的增大而逐渐变小，由于该套轴承只适用于极小转速的工况，当转速达到12 r/min时，R=72.83%<90%，可靠性迅速降低，工作性能不可靠，说明不确定的增加会伴有可靠性的降低，两者之间具有明显的负相关关系，可借用灰关系进行关联判定。

对轴承摩擦力矩不确定性与可靠性进行灰关系分析时，取参数f1,2=0.5，由表3可知，两者之间为负相关关系。为使两者极性统一，计算时将其中一属性添加负号，即得到两个矢量序列Φ1=(-0.0838,-0.0970,-2143)、Φ2=(0.9792,0.9675,0.7283)，对两序列归一化处理，得到规范化生成序列G1和G2，结果如图6所示。

图6 Φ1和Φ2序列归一化处理结果(案例3)Fig.6 Normalization processing results of seriesΦ1 and Φ2(case 3)

由图6可知，Φ1和Φ2两序列归一化处理后所得的规范化序列G1和G2的整体变化趋势十分相似，且两者几乎完全重合，即两者关系十分紧密，且紧密程度高于案例2。为有力说明两序列的紧密程度，在给定参数f1,2=0.5条件下，求出两者之间的灰置信水平为99.55%≥90%。所以Φ1和Φ2两序列关联紧密，进而说明轴承摩擦力矩性能不确定性与可靠性之间为负相关关系，可信水平达到99.55%。该实验数据的分析结果显示，随着滚动轴承转速的增大，摩擦力矩性能不确定性呈现出非线性增长趋势，可靠性呈现非线性降低趋势；且不确定性和可靠性之间存在明显的灰关系。

显然，三个案例的建模分析均有效地反映出轴承振动与摩擦力矩性能的一般变化规律，准确地监测出轴承服役期间性能不确定性及可靠性演变轨迹，且两者之间存在紧密关系，均呈现出非线性的增大或减小趋势。三个案例单独进行且三者之间毫无联系，其性能不确定性与可靠性之间的灰置信水平是独立存在的，即三个灰置信水平结果的数值差异是必然存在的，但只要其数值大于一定值(90%)，便可说明滚动轴承的性能不确定性与可靠性之间存在紧密的灰关系。实验结果表明三个案例的灰置信水平均大于90%，最高达到99.55%，最低也高于95.00%，所以滚动轴承性能不确定性与可靠性关系紧密。因此所提方法可以有效地挖掘轴承性能时间序列的变化信息，通过分析其性能不确定性、可靠性以及两者之间的灰关系，可有效监测轴承内部已发生的潜在失效状况。

3 结论

(1)以灰自助原理求得的平均动态波动来量化滚动轴承性能不确定性，可很好地识别出轴承振动随磨损直径与时长的演变过程，以及摩擦力矩随转速变化的特征规律。

(2)计数过程求得的变异强度可有效表征滚动轴承性能时间序列变异程度，泊松方程准确预测出轴承性能可靠性的退变历程，进而实现早期故障征兆的识别与提取。

(3)轴承服役期间，其振动性能不确定性随转速与时长的增加呈现出非线性增长趋势，可靠性逐渐降低；其摩擦力矩不确定性随转速增加同样呈现出非线性增长趋势，可靠性也随之降低；不确定性或可靠性无论如何变化，两者之间均存在明显的灰关系，灰置信水平在95%以上。

(4)本文所提模型可以有效地同时监控轴承性能不确定性与可靠性的演变状况，且揭示出两者之间的内在联系并实现了统一评价。

[1] LONDHE N D, ARAKERE N K, HAFTKA R T. Reevaluation of Rolling Element Bearing Load-life Equation Based on Fatigue Endurance Data[J]. Tribology Transactions, 2015, 58(5):815-828.

[2] CAMCI F, MEDJAHER K, ZERHOUNI N, et al. Feature Evaluation for Effective Bearing Prognostics[J]. Quality & Reliability Engineering, 2013, 29(4):477-486.

[3] WANG Shuang, JIANG Xiumin, WANG Qian, et al. Experiment and Grey Relational Analysis of Seaweed Particle Combustion in a Fluidized Bed[J]. Energy Conversion & Management, 2013, 66(1):115-120.

[4] ZHOU Q, THAI V V. Fuzzy and Grey Theories in Failure Mode and Effect Analysis for Tanker Equipment Failure Prediction[J]. Safety Science, 2015, 83:74-79.

[5] KYDYRBEKULY A, KHAJIYEVA L, GULAMA-GARYP A Y, et al. Nonlinear Vibrations of a Rotor-fluid-foundation System Supported by Rolling Bearings[J]. Strojniski Vestnik, 2016, 62(6):351-362.

[6] MATS’KO I I, YAVORS’KYI I M, YUZEFOVYCH R M, et al. Stochastic Dynamic Model of the Vibration Signals of Rolling Bearing and Their Analysis[J]. Materials Science, 2014, 49(4):549-559.

[7] TONG V C, HONG S W. The Effect of Angular Misalignment on the Running Torques of Tapered Roller Bearings[J]. Tribology International, 2016, 95(4):76-85.

[8] DINDAR A, AKKOK M, CALISKAN M. Experimental Determination and Analytical Model of Friction Torque of a Double Row Roller Slewing Bearing [J]. Journal of Tribology, 2017,139(2):021503.

[9] 孙强, 岳继光. 基于不确定性的故障预测方法综述[J]. 控制与决策, 2014, 29(5):769-778. SUN Qiang, YUE Jiguang.Review on Fault Prognostic Methods Based on Uncertainty[J]. Control and Decision, 2014, 29(5):769-778.

[10] KAUSCHINGER B, SCHROEDER S. Uncertainties in Heat Loss Models of Rolling Bearings of Machine Tools [J]. Procedia CIRP, 2016, 46:107-110.

[11] 刘志成, 姜潮, 李源,等. 考虑焊点不确定性的车身点焊结构疲劳寿命优化[J]. 中国机械工程, 2015, 26(18):2544-2549. LIU Zhicheng, JIANG Chao, LI Yuan, et al. Fatigue Life Optimization for Spot-welded Structures of Vehicle Body Considering Uncertainty of Welding Spots[J]. China Mechanical Engineering, 2015, 26(18):2544-2549.

[12] XIA Xintao, CHEN Long, MENG Fannian. Uncertainty of Rolling Bearing Friction Torque as Data Series Using Grey Bootstrap Method[J]. Applied Mechanics & Materials, 2010, 44-47:1125-1129.

[13] XIA Xintao, CHEN Long. Fuzzy Chaos Method for Evaluation of Nonlinearly Evolutionary Process of Rolling Bearing Performance[J]. Measurement, 2013, 46(3):1349-1354.

[14] 高攀东, 沈雪瑾, 陈晓阳,等. 无失效数据下航空轴承的可靠性分析[J]. 航空动力学报, 2015, 30(8):1980-1987. GAO Pandong, SHEN Xuejin, CHEN Xiaoyang, et al. Reliability Analysis for Aircraft Bearing with Zero-failure Data[J]. Journal of Aerospace Power, 2015, 30(8):1980-1987.

[15] 朱德馨, 刘宏昭, 原大宁,等. 高速列车轴承可靠性试验时间的确定及可靠性寿命评估[J]. 中国机械工程, 2014, 25(21):2886-2891. ZHU Dexin, LIU Hongzhao, YUAN Daning, et al. Time Determination and Life Assessment of High-speed Railway Bearing Reliability Test[J]. China Mechanical Engineering, 2014, 25(21):2886-2891.

[16] GRASSO M, CHATTERTON S, PENNACCHI P, et al. A Data-driven Method to Enhance Vibration Signal Decomposition for Rolling Bearing Fault Analysis[J]. Mechanical Systems & Signal Processing, 2016, 81:126-147.

[17] ALI J B, FNAIECH N, SAIDI L, et al. Application of Empirical Mode Decomposition and Artificial Neural Network for Automatic Bearing Fault Diagnosis Based on Vibration Signals[J]. Applied Acoustics, 2015, 89(3):16-27.

[18] KATSIFARAKIS N, RIGA M, VOUKANTSIS D, et al. Computational Intelligence Methods for Rolling Bearing Fault Detection[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2016, 38(6):1565-1574.

[19] SEHGAL R, GANDHI O P, ANGRA S. Reliability Evaluation and Selection of Rolling Element Bearings[J]. Reliability Engineering & System Safety, 2000, 68(1):39-52.

[20] LI Hongkun, ZHANG Zhixin, LI Xiugang, et al. Reliability Prediction Method Based on State Space Model for Rolling Element Bearing[J]. Journal of Shanghai Jiaotong University (Science), 2015, 20(3):317-321.

[21] 刘英, 余武, 李岳,等. 基于区间灰色系统理论的可靠性分配[J]. 中国机械工程, 2015, 26(11):1521-1526. LIU Ying, YU Wu, LI Yue, et al. Reliability Allocation Based on Interval Analysis and Grey System Theory[J]. China Mechanical Engineering, 2015, 26(11):1521-1526.

[22] PANDA S, MISHRA D, BISWAL B B, et al. Optimization of Multiple Response Characteristics of EDM Process Using Taguchi-based Grey Relational Analysis and Modified PSO[J]. Journal of Advanced Manufacturing Systems, 2015, 14(3):123-148.

[23] KUMAR S S, UTHAYAKUMAR M, KUMARAN S T, et al. Parametric Optimization of Wire Electrical Discharge Machining on Aluminium Based Composites through Grey Relational Analysis[J]. Journal of Manufacturing Processes, 2015, 20:33-39.

[24] 邓聚龙.灰理论基础[M].武汉: 华中科技大学出版社, 2002: 50-200. DENG Julong. Grey Theory Basis[M]. Wuhan: Huazhong University of Science and Technology Press, 2002:50-200.

[25] XIA Xintao, CHEN Xiaoyang, ZHANG Yongzhen, et al. Grey Bootstrap Method of Evaluation of Uncertainty in Dynamic Measurement[J]. Measurement, 2008, 41(6):687-696.

(编辑王旻玥)

EvaluationofRollingBearingPerformanceUncertaintyandReliability

CHANG Zhen1XIA Xintao1,2LI Yunfei1LIU Hongbin1
1.Mechanical Engineering College,Henan University of Science and Technology,Luoyang,Henan,471003 2.Collaborative Innovation Center of Machinery Equipment Advanced Manufacturing of Henan Province,Henan University of Science and Technology,Luoyang, Henan,471003

Based on the grey system theory and Poisson counting process, the performance uncertainty of rolling bearings was quantified by a parameter, and the performance reliability of the bearings under different working conditions was analyzed via setting threshold value, then the performance matching sequences of uncertainty and reliability were established to find out the internal connection between the two items in bearing service processes. According to a property time series during the bearing operations, its uncertainty was obtained by grey bootstrap processing. Referencing the setting threshold to Poisson count, the time series effective variation strength was gained, then the performance reliability was acquired. Finally, the grey relation between uncertainty and reliability was analyzed. Experimental results show that the evolution information of rolling bearing performance uncertainty and reliability may be really described, the normalization processing results of the two are very similar and presenting obvious grey relation. The experimental results of various cases keep good consistency.

rolling bearing; uncertainty; reliability; grey relation

2017-02-27

国家自然科学基金资助项目(51475144,U1404517)；河南省自然科学基金资助项目(162300410065)

TH133；TB114

10.3969/j.issn.1004-132X.2017.18.010

常振，男，1992年生。河南科技大学机电工程学院硕士研究生。主要研究方向为滚动轴承性能可靠性、稳定性、不确定性等。夏新涛(通信作者)，男，1957年生。河南科技大学机电工程学院教授、博士研究生导师。E-mail: xiaxt1957@163.com。李云飞，男，1992年生。河南科技大学机电工程学院硕士研究生。刘红彬，男，1974年生。河南科技大学机电工程学院副教授、博士。