摇摆工况下错位瓦轴承支撑的转子系统动力学特性

张 磊 裴世源 徐 华 张亚宾 朱 杰

1.西安交通大学现代设计及转子轴承系统教育部重点实验室，西安，7100492.湖南崇德工业科技有限公司，湘潭,411228

摇摆工况下错位瓦轴承支撑的转子系统动力学特性

张 磊1裴世源1徐 华1张亚宾2朱 杰2

1.西安交通大学现代设计及转子轴承系统教育部重点实验室，西安，7100492.湖南崇德工业科技有限公司，湘潭,411228

基于轴承刚度和阻尼的分段线性化假设，建立了不同横摇角度的转子轴承模型；利用DLAP软件，耦合求解错位瓦轴承支撑的转子系统的动力学模型；采用特征值和特征向量、不平衡响应分析、稳定性分析和瞬态动力学分析等手段，研究了轴系的稳定性和安全性，并与正常工况下轴系的动力学特性对比，得到了摇摆工况下错位瓦轴承支撑的转子系统的动力学特性。

摇摆工况；错位瓦轴承；转子动力学；分段线性化

0 引言

舰船在海上航行时，海风波浪等各种扰动因素的冲击，会使舰船发生低频的横摇和纵摇等摇摆运动，尽管船体纵摇和横摇运动产生的振动频率远远低于舰船轴承转子系统的转速，但这些振动还是会通过轴承油膜力对舰船动力装置转子系统的动力学特性产生很大的影响，从而对轴承支撑的转子系统的稳定性产生影响。因此，为了提高舰船在倾斜摇摆等复杂海况下航行时的稳定性和安全性，很有必要针对摇摆工况下错位瓦轴承支撑的转子系统的动力学特性进行深入分析和研究。

关于转子轴承系统的动力学特性的研究，许多学者投入其中并在理论和实验研究方面取得了一系列成果。文献[1]用状态空间Newmark有限元瞬态响应分析方法研究了冲击激励作用下转子轴承系统的响应，并进行试验对比验证；文献[2]研究了周期性摆角运动对柔性转子轴承系统运行参数稳定性的影响；文献[3]研究了舰船纵横倾作用下转子轴承系统的动力学特性，得到了摇摆参数对系统动力学特性的影响；文献[4]研究了歪斜安装对组配轴承转子系统动力学特性的影响，发现合理利用轴承歪斜后的非均匀间隙特性，有助于改善系统运行的动力特性；文献[5]针对表面织构对转子轴承系统的稳定性影响进行了实验研究，发现合理的表面织构设计，可以有效提高径向滑动轴承支撑的转子系统的稳定性；文献[6]研究了机械密封对转子轴承系统动力学性能的影响，发现柔性的转子轴承系统端面密封的存在可使系统的一阶阻尼临界转速得到提高。

以上学者分别在不同工况条件下对转子轴承系统动力学特性进行研究，取得了有意义的成果，但是目前在摇摆工况下，针对错位瓦轴承支撑的转子系统的动力学特性的研究工作非常少。本文以某舰船发电机错位瓦转子轴承系统为例，研究错位瓦轴承的润滑特性，通过分析轴承的关键运行参数，证明错位瓦轴承在正常工况下的安全性；接着针对摇摆工况，利用轴承刚度和阻尼分段线性化假设，建立错位瓦轴承支撑的转子系统动力学模型，通过专业转子动力学软件DLAP耦合求解轴承转子系统动力学方程，详细研究了包括转子的临界转速、系统的稳定性分析、不平衡响应和瞬态动力学分析等动力学特性，从而验证错位瓦轴承转子系统的稳定性。

1 错位瓦轴承润滑特性

润滑特性分析是在正常工况下，采用本课题组研发的转子轴承系统计算软件DLAP求解包含瞬态项的Reynolds方程和温黏方程，研究错位瓦轴承的安全性。通过分析错位瓦轴承关键的运行参数如最小油膜厚度、最大油膜压力、温升、功耗和流量，判断轴承在正常工况下的安全性，并验证DLAP软件计算结果的正确性。

为研究轴承流体润滑系统的摩擦学性能，经典方法是借助有限元或有限差分等数值方法，通过求解Reynolds方程得到压力分布后，进而求得其他统计量，如摩擦力(矩)、承载力以及摩擦因数等。各种流体润滑问题都涉及在微小间隙中的黏性流动，描写这种物理现象的基本方程为Reynolds方程，它的普遍形式为

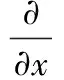
(1)

式中，h为油膜厚度，m；x为轴承周向展开方向的坐标，m；y为轴承轴向坐标，m；t为时间，s；p为油膜压力，Pa；u、v分别为轴颈相对轴瓦的相对速度的切向分量和径向分量；μ为润滑介质动力黏度，Pa·s；ρ为流体密度，kg/m3。

式(1)是典型的椭圆型偏微分方程，仅在特殊情况(如一维倾斜滑块)下才可能求得解析解，通常情况下无法用解析方法求解精确解。数值方法是求解该润滑问题的有效途径，本课题组自主研发了计算软件DLAP，采用有限元法求解包含瞬态项的Reynolds方程和温黏方程。虽然有限元计算过程较为复杂，但该方法计算过程中的每个模块均已成熟，如单元形函数的选择、单元刚度矩阵形成、整体刚度矩阵的组装以及代数方程组的求解等模块均已标准化,因此，采用有限元法对Reynolds方程进行求解比较合理。DLAP软件的润滑特性计算结果如图1所示。

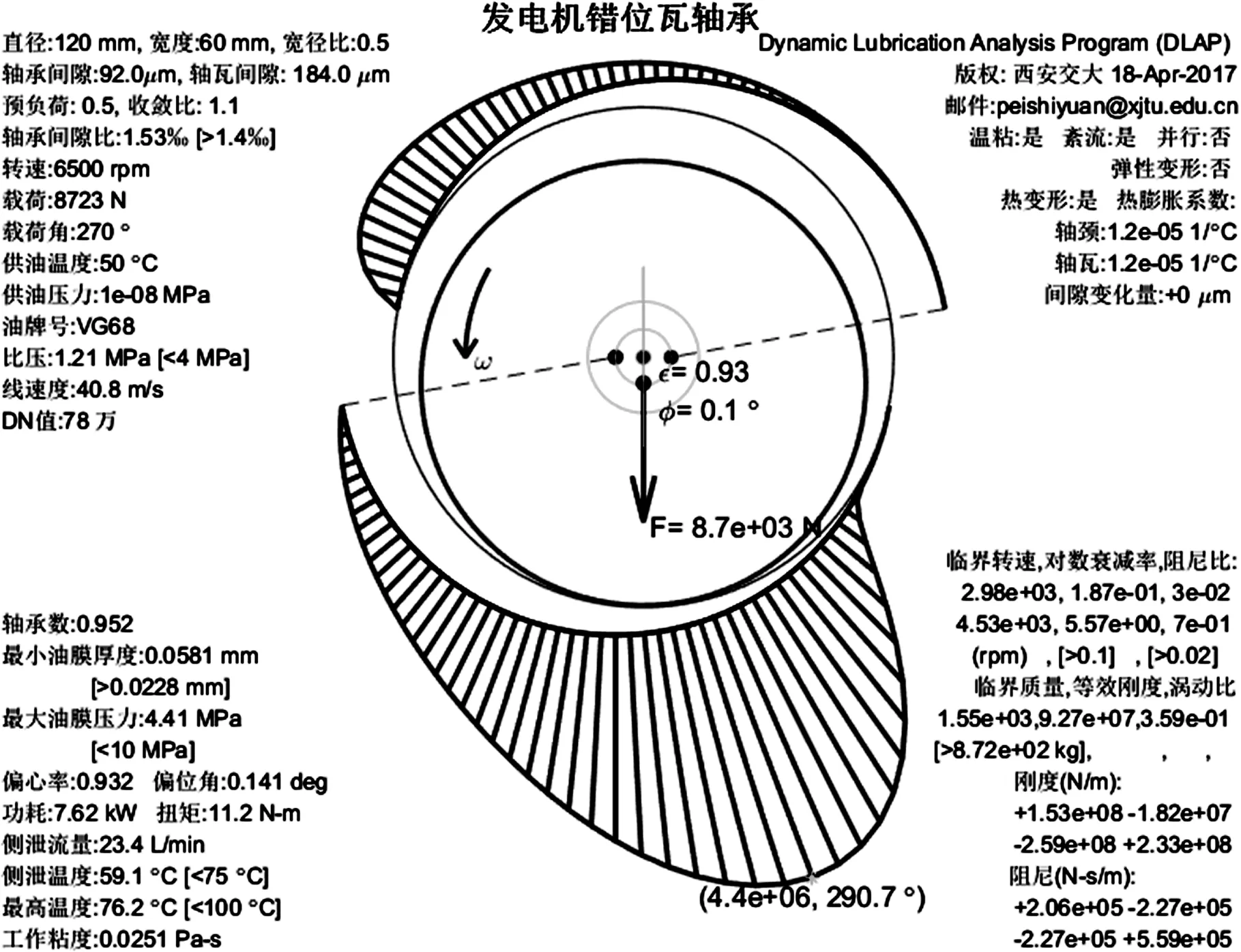
(a)6500 r/min

(b)7500 r/min图1 错位瓦轴承润滑特性参数Fig.1 Lubrication characteristic parameters of offset bearing

正常工况下根据表1的参数，利用DLAP软件对错位瓦轴承进行润滑特性计算分析，得到载荷竖直向下、转速n为6500 r/min和7500 r/min的计算结果，如表2所示。对计算结果进行对比分析，可以看出错位瓦轴承的温升、最小油膜厚度和流量均满足使用要求，该设计参数满足工况要求。

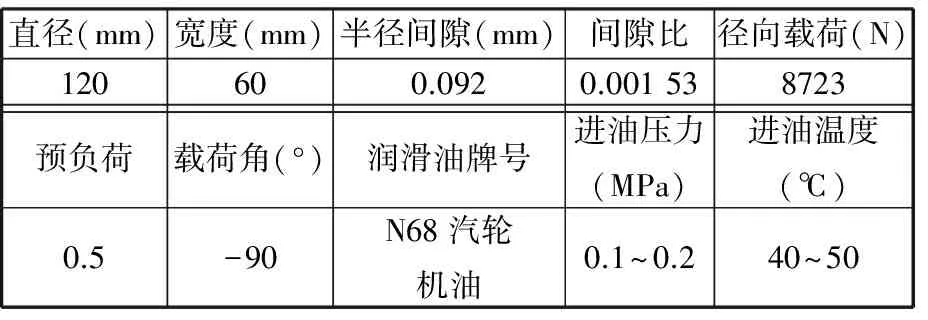
表1 错位瓦轴承参数

表2 计算结果

2 倾斜和摇摆环境

在海面停泊或航行的舰船由于波浪的强迫摇摆和舰船本身固有的摇摆，舰船动力装置轴承转子系统不可避免地随着舰船平台出现平移、旋转等运动，主要表现为倾斜环境和摇摆环境。

倾斜环境包括横倾和纵倾，横倾和纵倾这两种状态指舰船相对于设计水线具有横向倾斜的浮态和纵向倾斜的浮态。摇摆环境包括横摇和纵摇，横摇和纵摇这两种状态指舰船绕其横轴、纵轴所作的周期性角位移运动[7]。由于倾斜和摇摆的作用，安装在舰船上的设备在结构强度、工作性能和精度等方面会受到一定程度的影响。如破坏设备内部作用力平衡、改变轴承受力条件、液态介质溢出和仪表显示失常等。因此，为确保设备的可靠性，对于在倾斜和摇摆状态下性能受到影响或具有旋转运动、液态介质和重力不平衡运动系统的设备，要求进行倾斜和摇摆计算分析和试验，以考核、评定设备在此环境下工作的适应性和结构的完好性。

倾斜试验的严酷等级由倾斜角度和试验持续时间两个参数确定；摇摆试验的严酷等级由摇摆角度(纵摇、横摇、首摇)或线加速度幅值(纵荡、横荡、垂荡)、摇摆周期和试验持续时间等3个参数确定[8]。倾斜和摇摆环境严酷度的定量值根据需求和预测的倾斜和摇摆环境状态确定。本文使用GJB150.23A-2009标准中规定的水面舰船和潜艇设备的试验严酷等级来分析研究(表3)。

表3 中国海军舰船装备倾斜和摇摆环境严酷度

注：*表示具体角度由产品规范规定

图2 摇摆工况示意图Fig.2 Schematic of rolling condition

本文主要研究摇摆环境下，错位瓦轴承转子系统的动力学特性，由于纵摇±10°不会对转子的横向振动产生明显影响，所以重点考虑横摇±45°工况。图2为横摇工况示意图，外圈上下两个错位圆代表错位瓦轴承，中心圆代表轴颈，箭头代表横摇工况下轴颈受力方向。在正常工况，舰船不发生摇摆，受力方向不变,竖直向下(力为自身重力)；当处于摇摆工况时，转子轴承系统左右摇摆，受力方向竖直向下。可以假设转子轴承系统固定不动，受力方向在±45°范围内摆动，从而使摇摆工况得到合理的转化。

3 分段线性化假设

根据GJB 150.23A-2009标准，选择5 s内摇摆±45°的工况进行分析计算。竖直向下径向载荷在此横摇条件下，沿x和y方向载荷分量的变化如图3所示。利用DLAP软件逐步求解Reynolds方程,在时域采用RK方法逐步积分，计算摇摆工况下错位瓦轴承的轴心轨迹、最大油膜压力和最小油膜厚度的变化。计算结果如图4、图5所示。

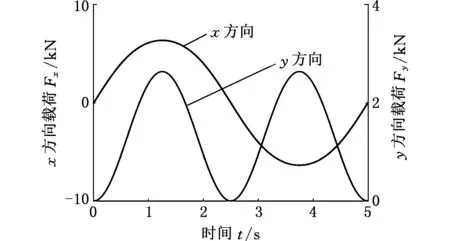
图3 摇摆工况轴承的载荷变化Fig.3 Load change of bearing under rolling condition

图4 摇摆工况下错位瓦轴承轴心轨迹Fig.4 Axis orbit of bearing under rolling condition

图4所示为摇摆工况下错位瓦轴承的轴心轨迹变化，其中实线圆为轴颈与轴承的间隙圆；曲线为轴心运动轨迹；圆点为轴心位置，它沿着曲线运动；箭头为受力方向，在摇摆工况下受力方向会在摇摆±45°范围摆动。通过观察轴心轨迹动态图可看出，摇摆工况下错位瓦轴承以纵摆为主，同时可以发现每个摇摆周期后，轴心均缓慢运动回到稳定平衡位置，并且轴心从平衡位置出发和返回的轨迹完全重合(轴心轨迹为一条曲线，而不是封闭圆)，因此转子的惯性效应不明显；由图5可知，摇摆工况下错位瓦轴承的油膜压力和最小油膜厚度变化平缓，证明错位瓦轴承适用于摇摆工况。

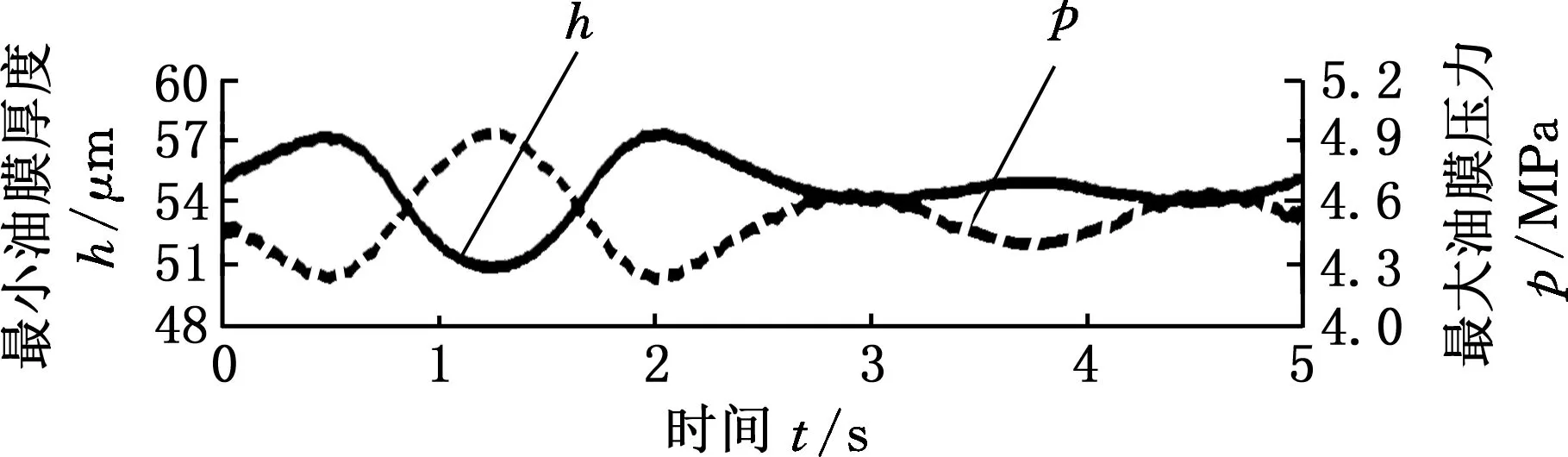
图5 摇摆工况下最大油膜压力和最小油膜厚度Fig.5 The maximum oil film pressure and the minimum oil film thickness under the rolling condition

由以上分析可得，轴心在整个摇摆周期内运动的惯性效应都不明显，因此可以把轴承的刚度和阻尼沿轴心轨迹线分段，在每一段轴承都有线性化的刚度和阻尼，这样既可以简化计算，也可以确保在不同的横摇角度下，分析转子动力学行为具有足够的精度。

具体做法是：假设轴心在-45°、-30°、-15°、15°、30°、45°不同的横摇角度为静平衡位置(转子在静平衡位置时轴承具有线性化的刚度和阻尼)，然后在这些横摇角度求解雷诺方程得到轴承的静特性，用小扰动法得到轴承在这些点的刚度和阻尼；再把轴心轨迹分段，以-45°、-30°、-15°、15°、30°、45°为中心，把轴心轨迹分为-45°～-37.5°、-37.5°～-22.5°、-22.5°～0°、0°～22.5°、22.5°～37.5°、37.5°～45°的6段，每一段的刚度和阻尼分别是以该段中心位置的横摇角度计算得到的刚度和阻尼。这样摇摆工况下的动态计算即可用静平衡位置的静态计算代替，在每一段具有确定的刚度和阻尼，省去了考虑轴心位置变化需要不断求解雷诺方程的过程，极大地简化了后续动力学计算。

4 转子动力学分析

动力学分析主要针对倾斜摇摆工况来研究舰船的动力装置转子轴承系统的动力学特性。通过建立错位瓦轴承支撑的转子系统动力学模型，利用DLAP软件，耦合求解滑动轴承和转子动力学模型，研究包括转子的临界转速、系统稳定性分析、不平衡响应和瞬态动力学分析等动力学特性。

4.1转子模型

根据舰船实际工况下转子工作数据，采用DLAP软件建立了错位瓦轴承支撑方案的转子模型，如图6所示。对于该转子轴承模型，采用转子自重作为静载荷计算轴承动特性系数；根据摇摆工况设置不同横摇角度，建立耦合求解错位瓦轴承和转子动力学的模型，进行转子动力学分析。错位瓦轴承的详细参数见表1。

图6 转子模型Fig.6 Rotor model

基于轴承刚度和阻尼的分段线性化假设，建立了两端轴承支撑的转子系统模型[9]。整个系统离散为26个节点，共25个单元。系统的振动微分方程为

式中，M为结构质量矩阵；C为阻尼矩阵；K为结构刚度矩阵；x为位移矩阵；F为载荷矩阵。

阻尼矩阵C考虑了陀螺效应和Rayleigh阻尼矩阵，Rayleigh阻尼矩阵为M和K的线性组合，即αM+βK，其中α和β是不依赖于频率的常数，它们与系统的阻尼系数和前两阶固有频率有关。F(t)由不平衡力和重力组成。不平衡力在下文不平衡响应分析中给出。

4.2轴承刚度和阻尼

轴承刚度和阻尼对转子的动力学特性具有决定性影响。确定转子轴承刚度和阻尼是计算转子-轴承系统临界转速的必须前提条件，因此需要首先求解轴承的刚度和阻尼。

4.2.1正常工况下轴承刚度和阻尼

本研究中，通过求解雷诺方程得到轴承的静特性，用小扰动法来求解线性化的刚度和阻尼。采用DLAP软件分析计算，得到正常工况下错位瓦轴承的刚度和阻尼随转速的变化情况如图7所示。

(a)刚度

(b)阻尼图 7 正常工况下错位瓦轴承刚度和阻尼Fig.7 Stiffness and damping of offset bearing under normal condition

图7a为轴承刚度随转速变化曲线，其中点是在不同转速下求解雷诺方程得到的刚度数据，Kxx曲线是x方向的刚度曲线，Kxy曲线是xy方向交叉刚度曲线，Kyx曲线是yx方向交叉刚度曲线，Kyy曲线是y方向的刚度曲线。图8、图9中的标注与图7相同。

以图7a中Kyy曲线为例,当转速为零时，轴心落在轴承底部，这时油膜厚度最小，油膜压力最大，刚度最大；随着转速的提高，轴心慢慢升高，远离轴承底部，油膜厚度增大，油膜压力减小，刚度也就逐渐减小；当轴心升高到接近轴承中心时，继续提高转速，轴心位置基本不变，刚度也基本不变。所以y方向刚度曲线趋势为先减小，然后基本趋于平稳。

4.2.2摇摆工况下轴承刚度和阻尼

根据实际倾斜摇摆工况和中国海军舰船装备倾斜和摇摆环境严酷度标准(表3)，基于轴承刚度和阻尼的分段线性化假设，分别建立横摇-30°、-15°、15°、30°的错位瓦轴承支撑的转子模型(横摇±45°计算过程和横摇±30°相同，而且横摇±30°可以满足实际工况要求)，利用DLAP软件计算倾斜摇摆工况下轴承刚度和阻尼，得到的计算结果如图8、图9所示。

4.3无阻尼临界转速

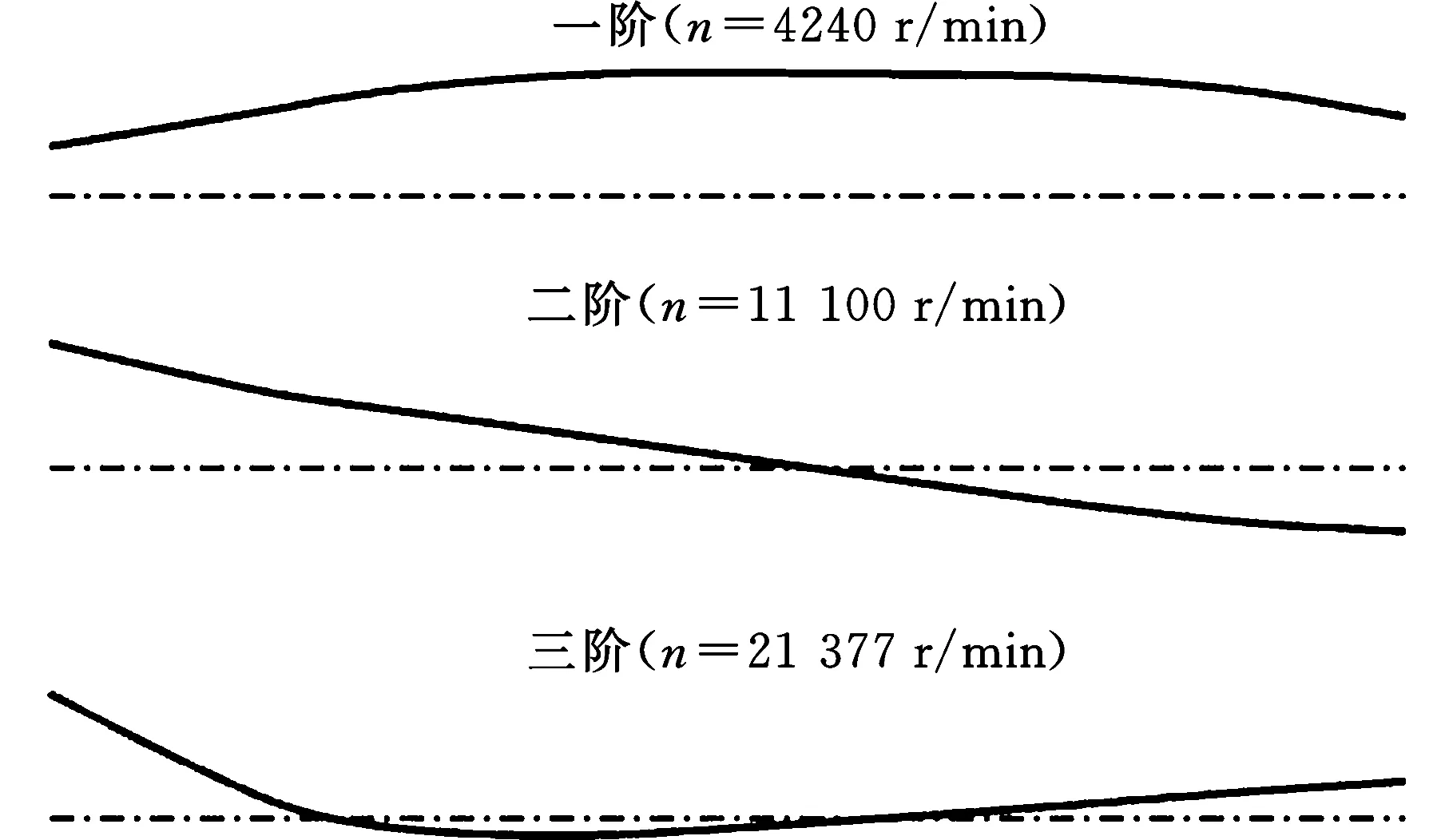
对转子系统进行无阻尼临界转速分析，轴承刚度分别取x和y方向的主刚度，得到转子的前三阶振型如图10所示，其中虚线为转子的平衡位置，实线为模态振型。

(a)横摇-30°

(b)横摇-15°

(c)横摇15°

(d)横摇30° 图8 摇摆工况下错位瓦轴承刚度Fig.8 Stiffness of offset bearing under rolling condition

由图10所示的x和y方向的动力学特性可知，第1阶振型中，转子中点无节点；在第2阶振型中，转子中点有一个节点；第3阶振型有2个节点。并且因为轴承在垂直和水平方向刚度不同，转子模态频没有重根，符合力学理论，验证了分析的正确性。

(a)横摇-30°

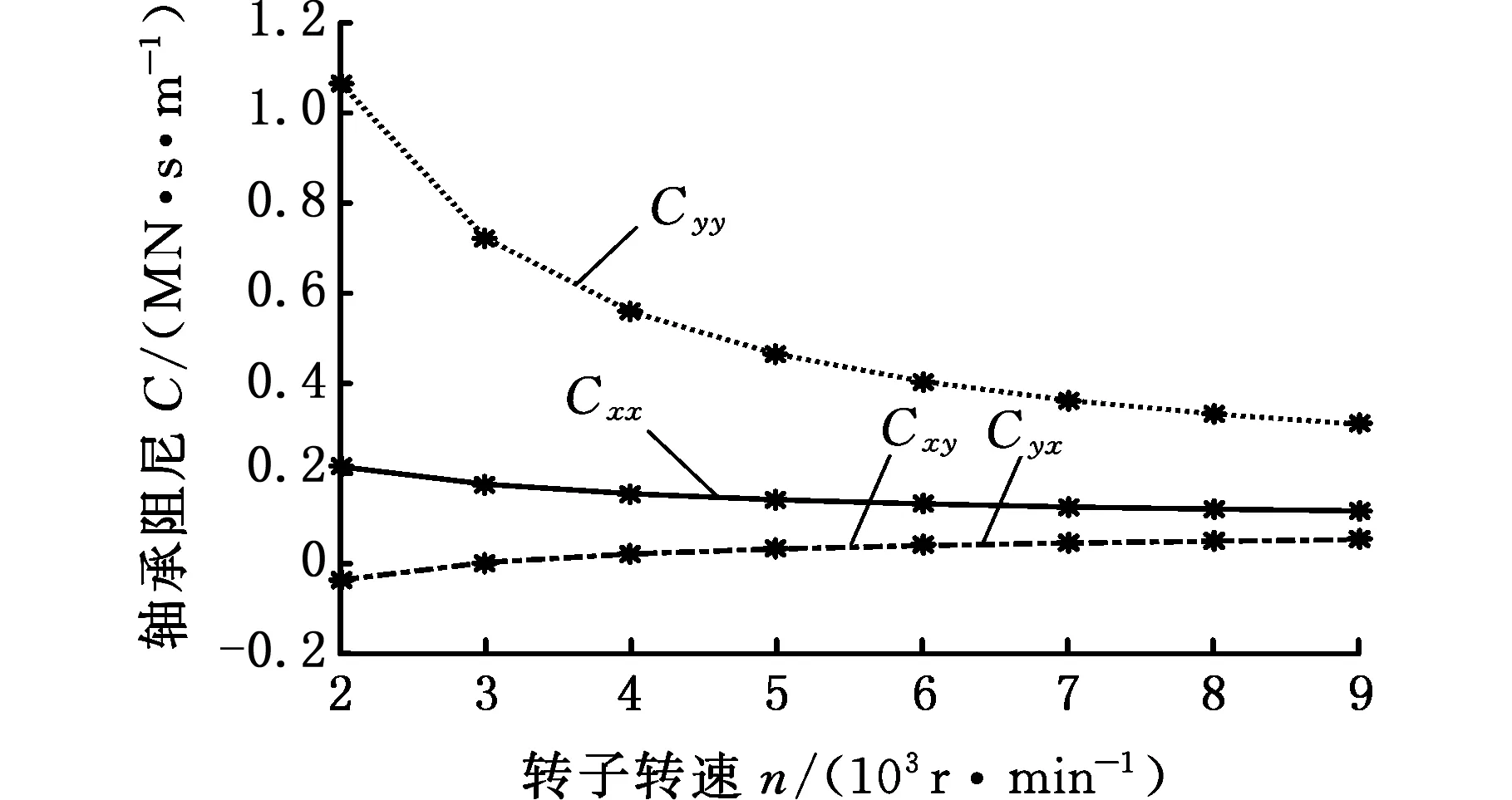
(b)横摇-15°

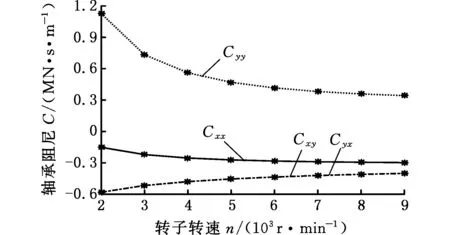
(c)横摇15°

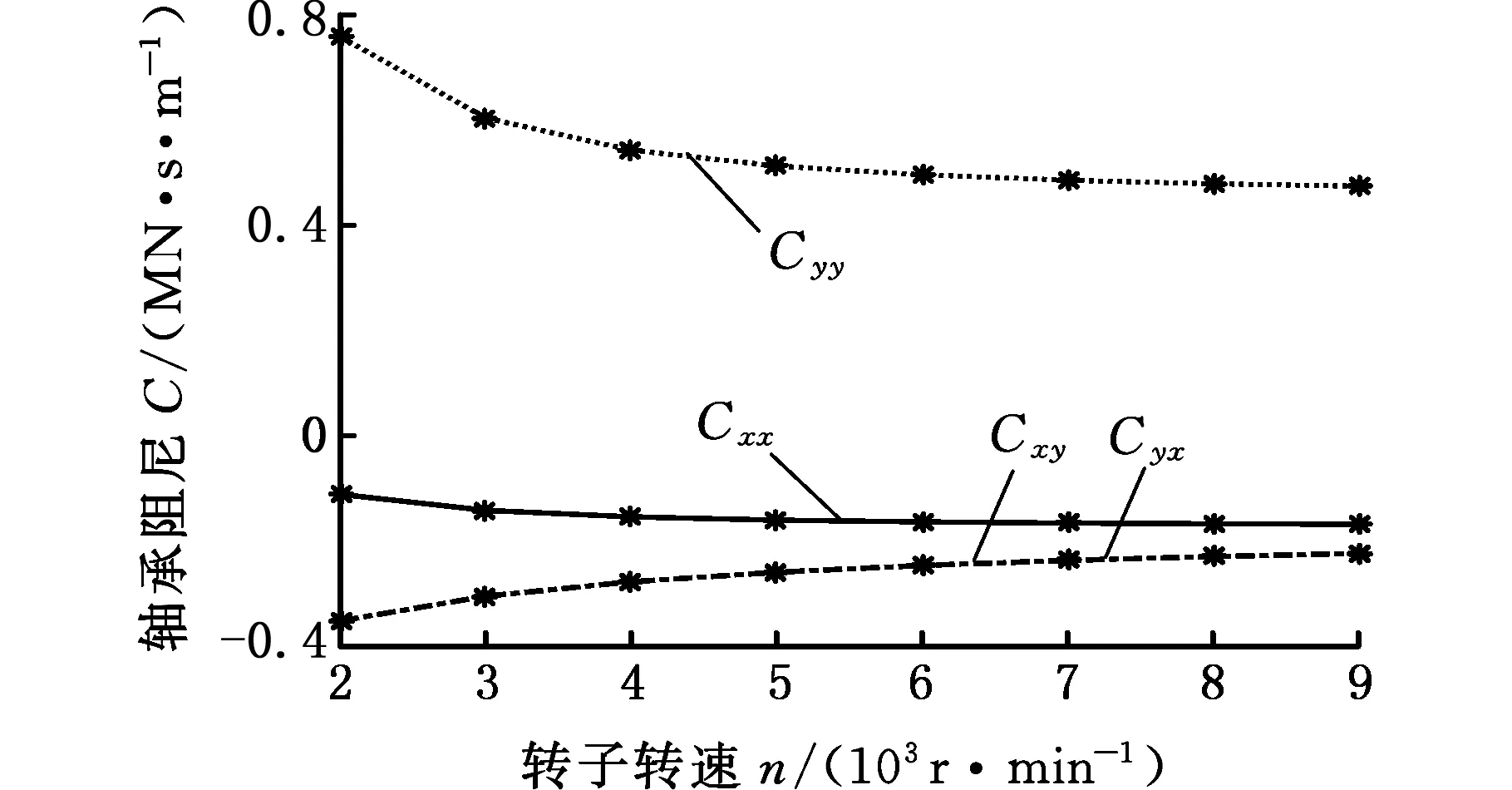
(d)横摇30° 图9 摇摆工况下错位瓦轴承阻尼Fig.9 Damping of offset bearing under rolling condition

由转子在6500 r/min下的临界转速及其振型可以看出，各阶临界转速与工作转速有足够大的隔离域值，转子在正常工况下运行不会出现共振或者过高的应力，验证了错位瓦轴承支撑的转子系统的安全性。

4.4无阻尼临界转速图与错位瓦轴承刚度

4.4.1正常工况下无阻尼临界转速图与错位瓦轴承刚度

(a)x方向主刚度的模态振型

(b)y方向主刚度的模态振型图10 错位瓦轴承支撑转子前三阶临界转速与模态振型Fig.10 The first three critical speeds and mode shapes of the rotor

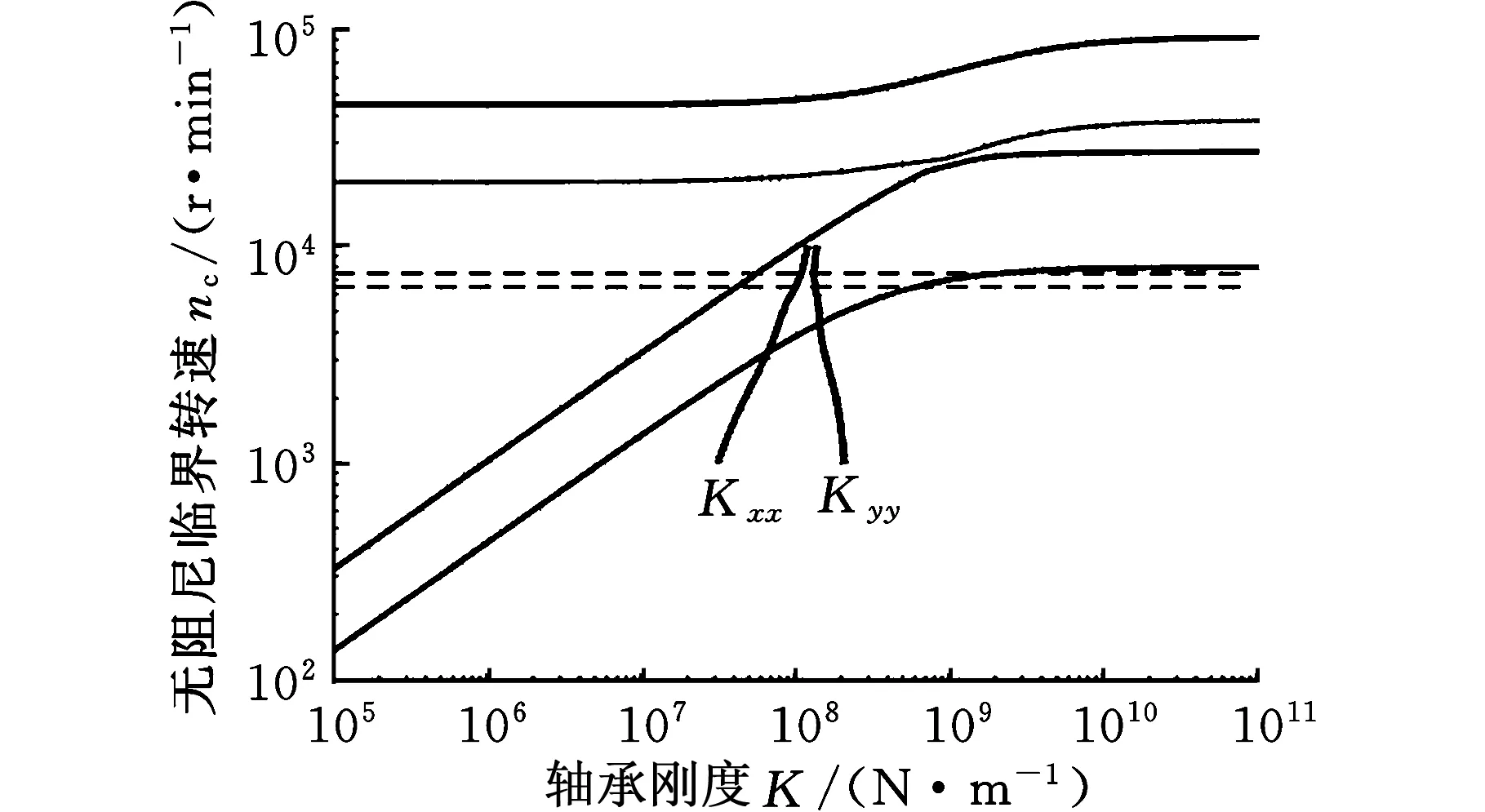
无阻尼临界转速随轴承支撑刚度的变化如图11所示。图11中4条实线曲线分别代表转子的前四阶临界转速，可以观察到随着轴承刚度的增大，各阶临界转速都升高；图11中，曲线Kxx、Kyy为通过图7得到的轴承x和y方向主刚度随转速变化曲线；两条虚线代表转子工作转速范围；刚度曲线和临界转速曲线的交点就是转子真实的临界转速值。图12曲线的意义和图11相同。

图11 正常工况下错位瓦轴承主刚度与无阻尼临界转速图Fig.11 Undamped critical speed and main bearing stiffness of offset bearing under normal condition

4.4.2摇摆工况下无阻尼临界转速图与错位瓦轴承刚度

通过图11和图12发现，在正常工况和摇摆工况下，临界转速曲线和刚度曲线的交点都在两条虚线的下方，也就是说，转子从启动至达到工作转速需要经过两个临界转速，但工作转速和临界转速有足够大的隔离裕度，所以转子转速越过临界转速后可以在工作转速下平稳运行。

(a)横摇-30°

(b)横摇-15°

(c)横摇15°

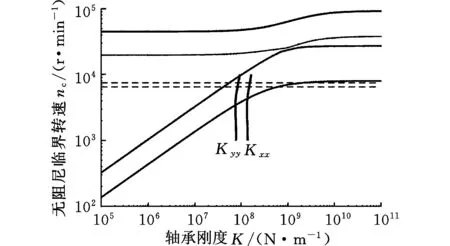
(d)横摇30°图12 摇摆工况下临界转速与错位瓦轴承主刚度Fig.12 Undamped critical speed and main bearing stiffness of offset bearing under rolling condition

4.5错位瓦轴承稳定性分析

根据API-684标准[10]，在工作转速内若对数衰减率大于0.1，表示系统具有足够的稳定裕度，无需进一步的稳定性分析；若对数衰减率小于0.1则系统稳定性不佳，需要做进一步分析；若对数衰减率小于0，则表示系统很可能发生失稳现象。对转子模型进行有阻尼特征值分析，可得到错位瓦轴承支撑方案下的对数衰减率，如图13所示。

图13 正常工况下错位瓦轴承支撑下转子的对数衰减率Fig.13 Logarithmic decay rate of the rotor supported by the offset bearing under normal condition

4.5.1正常工况下错位瓦轴承稳定性分析

如图13所示，在工作范围内错位瓦轴承支撑方案下的对数衰减率大于0.1，所以错位瓦轴承支撑的转子系统具有足够的稳定裕度。

4.5.2摇摆工况下错位瓦轴承稳定性分析

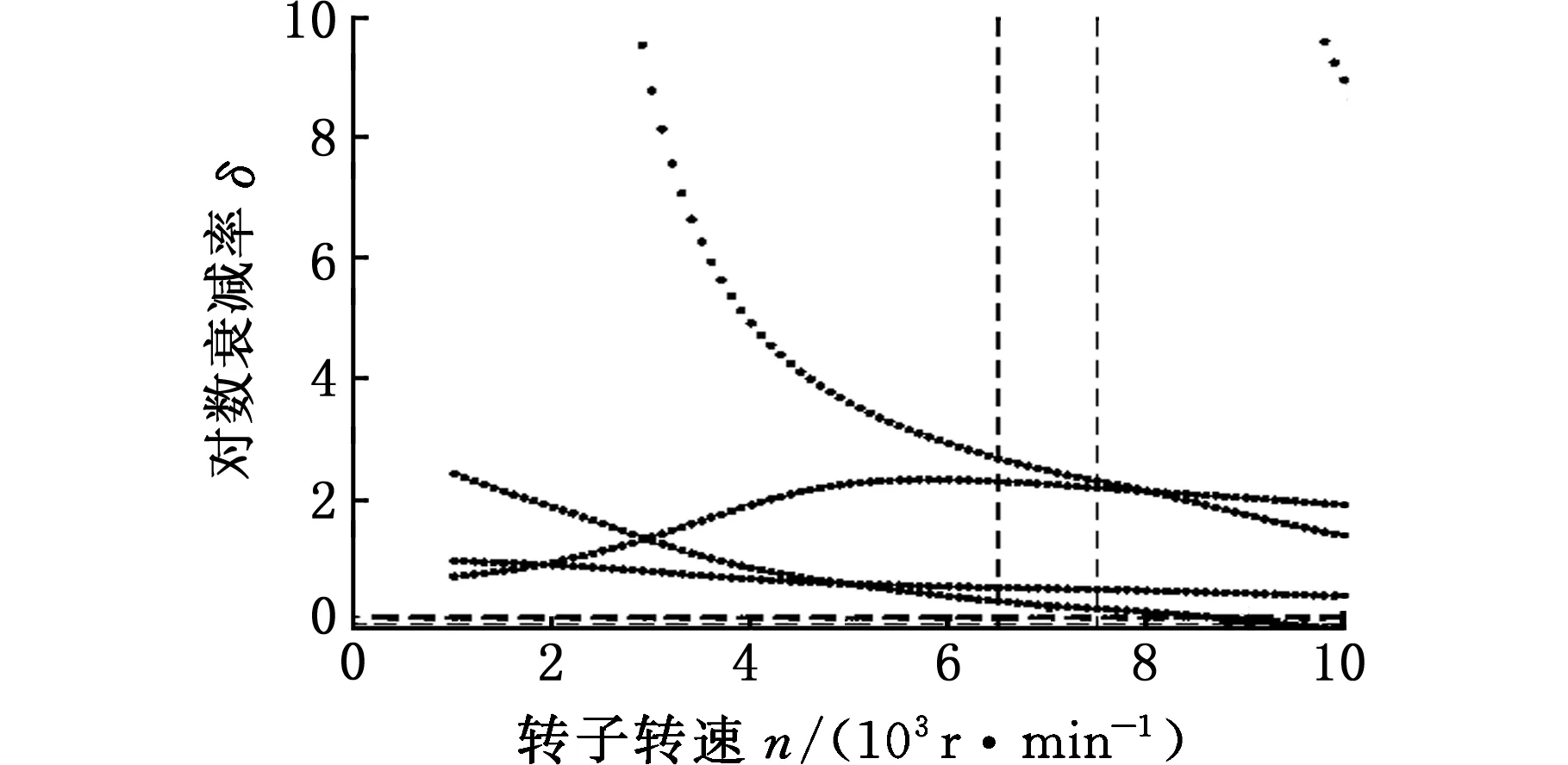
摇摆工况下，错位瓦轴承支撑转子的对数衰减率如图14所示。从图中观察到在6500～7500 r/min的工作范围内，对数衰减率全部大于0.1；在横摇-30°、15°情况下，转速大约为9500 r/min，远远超过工作转速时，才会出现对数衰减率小于0的情况，这表明在工作转速下系统具有足够的稳定裕度。

4.6不平衡响应分析

在转子动力学分析中稳态不平衡响应的计算与临界转速计算是同等重要的基本任务。不平衡响应分析也可以用来确定转子的临界转速，但它更重要的任务是求解转子系统在不平衡作用下的不平衡响应，分析研究如何限制最大不平衡响应。在不平衡响应计算结果中 ,可以得到转子在计算频域范围内的最大响应值 ,同时也可以得到工作转速范围内的最大响应值。

4.6.1正常工况下的不平衡响应分析

根据API-684标准计算可得转子的不平衡量限值为3.38 kg·mm，通过无阻尼临界转速和模态振型可知，在工作转速内，仅存在一阶临界转速，所以为了充分激发第一阶振型，在转子的中央位置16号节点添加不平衡量3.38 kg·mm。然后，在0～9000 r/min的范围内计算转子的不平衡响应。关于不平衡质量的大小和位置的更详细计算方法参阅API-684标准。对错位瓦轴承支撑的转子模型进行有阻尼谐响应分析，可得到各点转子的不平衡响应，其中前轴承处的x和y方向的位移随转速的变化如图15所示。

(a)横摇-30°

(b)横摇-15°

(c)横摇15°

(d)横摇30°图14 摇摆工况下错位瓦轴承支撑转子的对数衰减率Fig.14 Logarithmic decay rate of the rotor supported by the offset bearing under rolling condition

4.6.2摇摆工况下的不平衡响应分析

根据轴承刚度和阻尼分段线性化假设，分别对横摇-30°、-15°、15°、30°的错位瓦轴承支撑的转子模型进行有阻尼谐响应分析，可得到各点转子的不平衡响应，其中前轴承处的x和y方向的位移随转速的变化如图16所示。

由以上分析结果可以观察到前轴承6节点处x和y方向的位移随转速变化的曲线(Bode图)，从而得到共振的转速和振幅，如表4所示。在过临界转速时轴颈出现共振峰，正常工况下最大振幅峰值为5.37 μm ；在摇摆工况下，横摇-30°出现最大振幅峰值为7.79 μm；在工作转速6500～7500 r/min范围内，振幅都较小，符合工况要求。

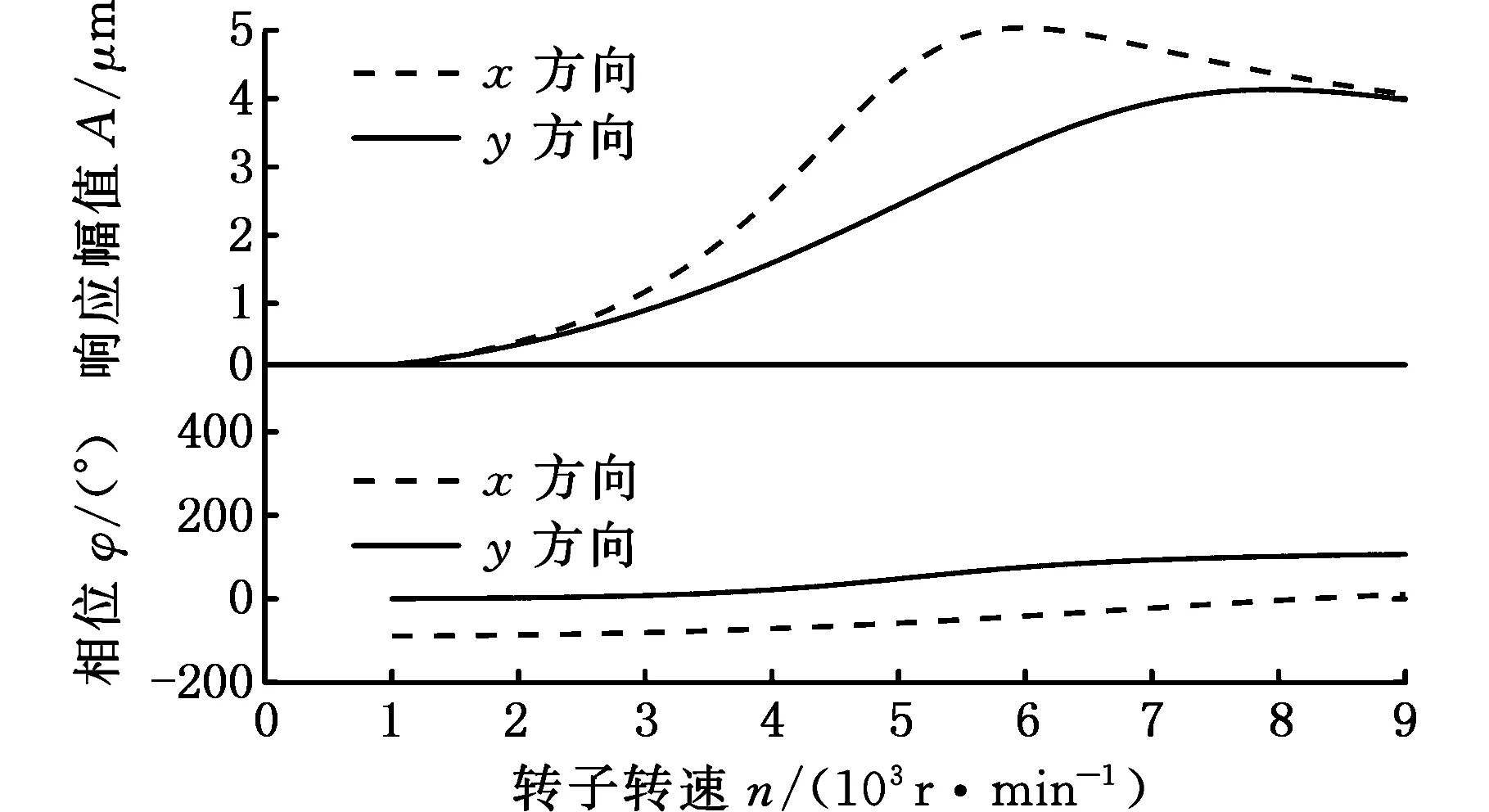
图15 正常工况下错位瓦轴承支撑转子的不平衡响应Fig.15 Unbalance response of the rotor supported by offset bearing under normal condition

(a)横摇-30°

(b)横摇-15°

(c)横摇15°

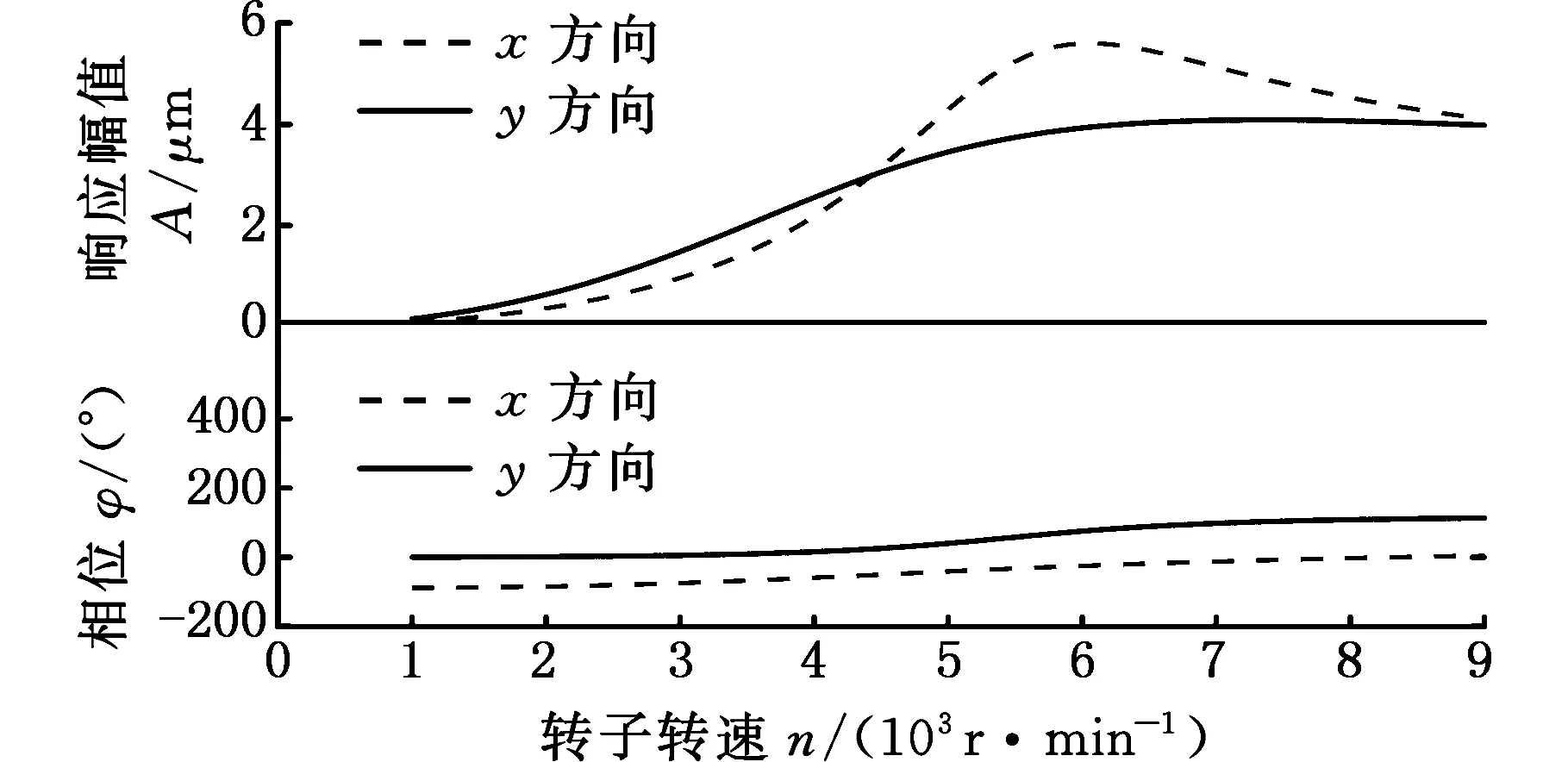
(d)横摇30°图16 摇摆工况下错位瓦轴承支撑转子的不平衡响应Fig.16 Unbalance response of the rotor supported by offset bearing under rolling condition

表4 不平衡响应幅值

由以上分析结果可知，在正常工况和摇摆工况下的幅频响应曲线峰值处放大系数AF都很小(小于1.5)，曲线变化很平缓，说明错位瓦轴承的阻尼特性好，具有较好的抗振性，有利于在摇摆工况下稳定运行。

4.7瞬态动力学响应

4.7.1正常工况下错位瓦轴承瞬态动力学响应

对转子模型进行全瞬态动力学分析可得到转子各点的位移随时间的变化，6500 r/min时前轴承处x和y方向的时域与频域分析如图17所示。

图17 正常工况下错位瓦轴承支撑轴颈处的时域与频域响应Fig.17 Transient dynamic response of the rotor supported by offset bearing under normal condition

4.7.2摇摆工况下错位瓦轴承瞬态动力学响应

摇摆工况下对转子模型进行全瞬态动力学分析，得到6500 r/min时前轴承处x和y方向的时域与频域分析如图18所示。

通过上面的瞬态动力学分析结果可以得到轴承支撑轴颈处的时域与频域响应。以轴承支撑处轴颈的振动为衡量标准，正常工况下，错位瓦支撑的轴颈振动很小，振幅约为5 μm，远小于间隙圆半径92 μm；摇摆工况下，轴承支撑处的轴颈的振动幅值约为6 μm，也远小于间隙圆半径，符合工况要求。

通过以上分析发现，在正常工况和摇摆工况下，轴颈的振动幅值都远小于间隙圆半径，轴颈振动属于小扰动，这验证了上文用小扰动法求解线性化的刚度阻尼的正确性，也证明了本文利用轴承刚度阻尼分段线性化假设来研究摇摆工况下转子轴承系统动力学特性的合理性。

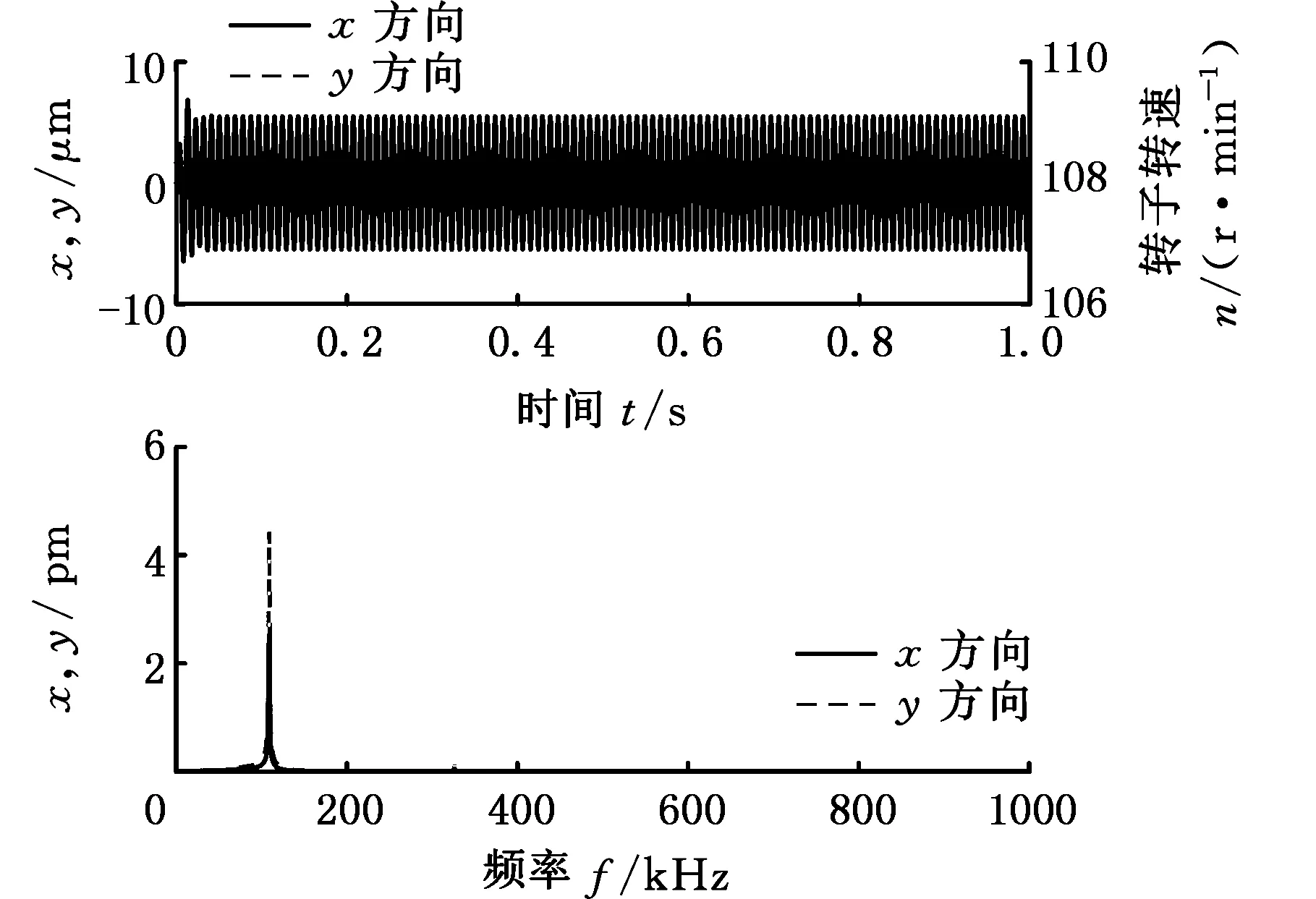
(a)横摇-30°

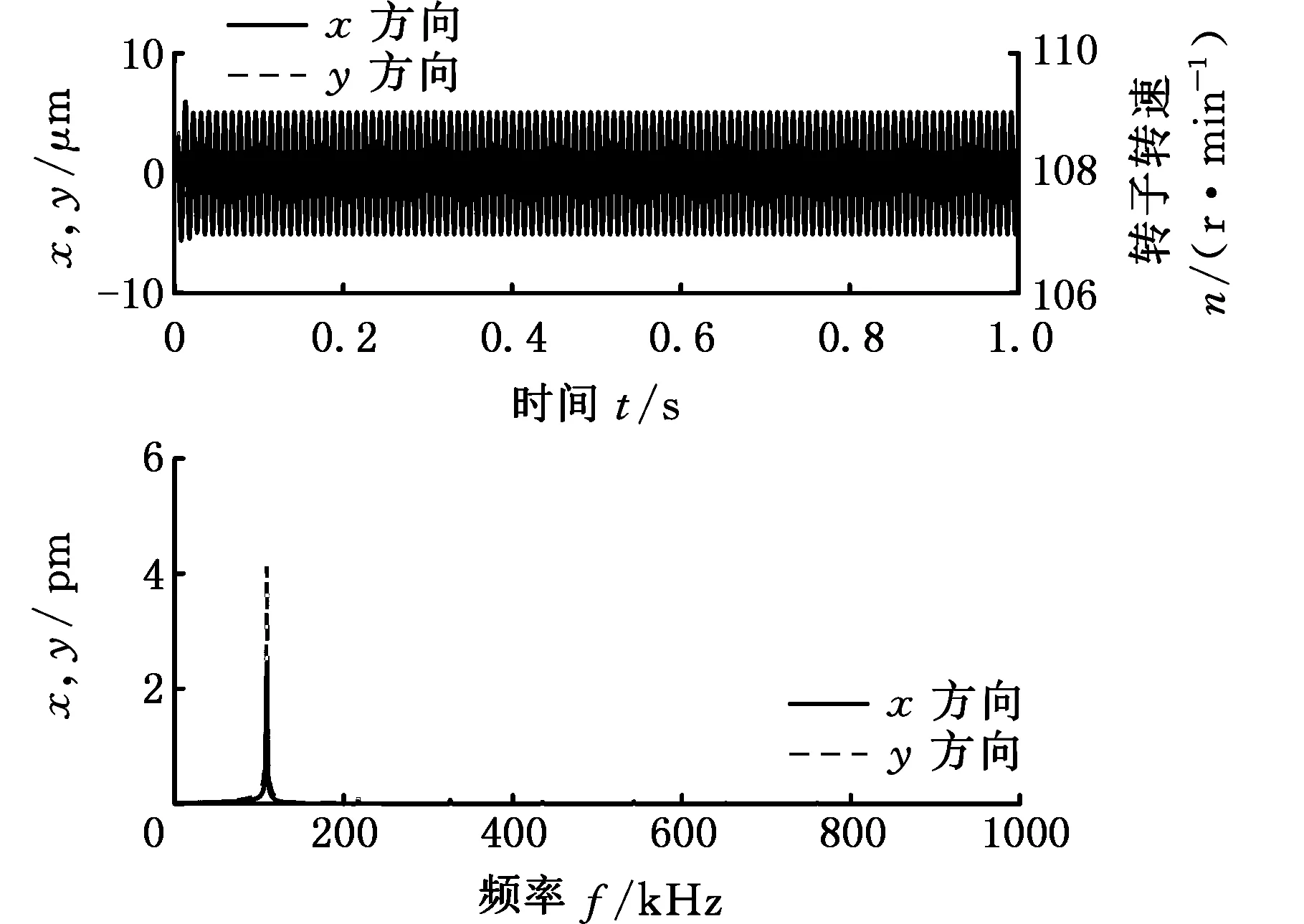
(b)横摇-15°

(c)横摇15°

(d)横摇30°图18 摇摆工况下错位瓦轴承支撑转子瞬态动力学响应Fig.18 Transient dynamic response of the rotor supported by offset bearing under rolling condition

5 结论

(1)在正常工况下进行润滑特性分析，错位瓦轴承的关键运行参数如最小油膜厚度、最大油膜压力、流量均满足使用要求，说明轴承参数满足工况要求；摇摆工况下，错位瓦轴承的最大油膜压力和最小油膜厚度变化平缓，证明错位瓦轴承适用于摇摆工况下工作。

(2)摇摆工况下，通过轴心轨迹的绘制发现转子在整个摇摆周期内惯性效应都不明显，因此可以沿着轴心轨迹对轴承刚度和阻尼进行分段线性化。这样不仅能够保证动力学分析的精度，而且将摇摆工况下的动态计算用静平衡位置的静态计算代替，在每一段具有确定的刚度和阻尼，省去了考虑轴心位置变化需要不断求解雷诺方程的过程，极大地简化了后续动力学计算。

(3)在工作转速下进行稳定性分析，结果表明，正常和摇摆工况的对数衰减率都大于0.1(API-684标准)，说明错位瓦轴承支撑的转子系统均具有足够的稳定裕度；不平衡响应分析的结果表明，在正常和摇摆工况下的幅频响应曲线变化平缓，说明错位瓦轴承具有很好的阻尼特性；瞬态动力学分析的结果表明，以错位瓦轴承支撑处的轴颈的振动为衡量标准，正常和摇摆工况，错位瓦轴承支撑的转子系统振动都很小，振幅远小于间隙圆半径(属于小扰动)，验证了上文用小扰动法求解线性化的刚度阻尼的正确性。综上可知，摇摆工况下，舰船机组选用错位瓦轴承，轴系具有较高的可靠性和稳定性。

[1] AN S L, KIM B O, KIM Y C. A Finite Element Transient Response Analysis Method of a Rotor-bearing System to Base Shock Excitations Using the State-Space Newmark Scheme and Comparisons with Experiments[J]. Journal of Sound & Vibration, 2006, 297(3/5):595-615.

[2] HAN Q, CHU F. Parametric Instability of Flexible Rotor-bearing System under Time-periodic Base Angular Motions[J]. Applied Mathematical Modelling, 2015, 39(15):4511-4522.

[3] 刘树鹏.舰船纵横倾作用下转子轴承系统动力学特性研究[D].哈尔滨：哈尔滨工业大学，2011. LIU Shupeng. Rotor Dynamic Characteristic of Rotor Bearing System for Ship with Vertical and Horizonal Swinging[D]. Harbin:Harbin Institute of Technology, 2011.

[4] 易均，刘恒，刘意，等.歪斜安装对组配轴承转子系统动力学特性影响[J].西安交通大学学报,2014,48(9):107-111. YI Jun, LIU Heng, LIU Yi, et al. Influence of Installed Outer Race on Nonlinear Dynamic Characteristics for Matched Bearings-Rotor System[J]. Journal of Xi’an Jiaotong University,2014,48(9):107-111.

[5] 王琳，裴世源，徐华.表面织构对转子轴承系统稳定性影响的实验研究[J]西安交通大学学报，2014,48(3):84-88. WANG Lin, PEI Shiyuan, XU Hua. Surface Texture Influence on Rotor-Bearing System Stability[J].Journal of Xi’an Jiaotong University,2014,48(3):84-88.

[6] 徐华，朱均.机械密封对转子轴承系统动力学性能的影响[J].西安交通大学学报,2004,38(7):665-670. XU Hua, ZHU Jun. Influence of the Mechanical Seals on the Dynamic Performance of Rotor Bearing System[J]. Journal of Xi’an Jiaotong University, 2004,38(7):665-670.

[7] 施建荣,施诗,张燕.论舰船装备倾斜和摇摆环境适应性与试验[J].装备环境工程,2011,8(4):41-44. SHI Jianrong, SHI Shi, ZHANG Yan. Discussion on Adaptability and Testing of Ship Equipment under Tilt and Swing Environment Condition[J]. Equipment Environmental Engineering, 2011,8(4):41-44.

[8] 黄国强.舰船机武器系统倾斜及摇摆实验方法探讨[J].航空标准化与质量,2012(4):12-13. HUANG Guoqiang. Discussion on the Experimental Method of Ship Machine Weapon System under Tilt and Swing Environment Condition[J]. Aeronautic Standardization Quality, 2012(4):12-13.

[9] 王正.转动机械的转子动力学设计[M].北京：清华大学出版社, 2015:76-97. WANG Zheng. Rotor Dynamic Design of Rotating Machinery[M]. Beijing:Tsinghua University Press, 2015:76-97.

[10] American Petroleum Institute. API 684-1996 Tutorial on the API Standard Paragraphs Covering Rotor Dynamics and Balancing:an Introduction to Lateral Critical and Train Torsional Analysis and Rotor Balancing[S]. Washington, D.C.:API Publication, 1996.

(编辑王旻玥)

DynamicsCharacteristicsofRotorSystemSupportedbyOffsetBearingsunderRollingConditions

ZHANG Lei1PEI Shiyuan1XU Hua1ZHANG Yabin2ZHU Jie2
1.Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System，Xi’an Jiaotong University，Xi’an，710049 2.Hunan SUND Industrial and Technological Co.,Ltd.，Xiangtan，Huaan,411228

Based on the assumption of piecewise linearization of bearing stiffnesses and dampings, a offset rotor-bearing model with different rolling angles was established. Using DLAP software, coupled solutions of the offset rotor-bearing system dynamics model was presented. By means of eigenvalue and eigenvector, unbalance response analysis, stability analysis and transient dynamics analysis, the stability and safety of the rotor-bearing system were studied, and compared with that under normal operating conditions. The dynamics characteristics of rotor system supported by offset bearings under rolling conditions were obtained.

rolling condition; offset bearing; rotor dynamics; piecewise linearization

2016-07-01

国家自然科学基金资助项目(51605367，51575421)；陕西省工业科技攻关项目(2015GY022)

TH113

10.3969/j.issn.1004-132X.2017.18.003

张磊，男，1988年生。西安交通大学机械工程学院博士研究生。主要研究方向为转子动力学、流体润滑理论、轴承智能控制。裴世源，男，1983年生。西安交通大学机械工程学院讲师。徐华，男，1956年生。西安交通大学机械学院教授、博士研究生导师。张亚宾，男，1981年生。湖南崇德工业科技有限公司工程师。朱杰，男，1981年生。湖南崇德工业科技有限公司总工程师。