关于Clapeyron 方程推导的探讨

刘 兴,赖 华,屈景年,曾荣英,李俊华

(衡阳师范学院化学与材料科学学院, 湖南 衡阳 421008)

关于Clapeyron方程推导的探讨

刘 兴,赖 华,屈景年,曾荣英,李俊华

(衡阳师范学院化学与材料科学学院,湖南衡阳421008)

Clapeyron 方程是物理化学中的一个重要方程, 本文从数学多元函数微分的角度出发，介绍了一种简洁、严密的Clapeyron 方程推导方法，对学习、研究该方程有一定参考意义。

Clapeyron 方程；多元函数；气液平衡； 数学

Clapeyron 方程是物理化学中的一个重要方程，在国内外公开出版的多种版本的物理化学教材中几乎都有介绍[1-3]。它是法国工程师Clapeyron 在1834年应用卡诺原理研究气-液平衡问题时提出的，这个时间早于热力学第二定律, 至今已有 l80多年的历史。该方程给出纯物质两相平衡的一般规律, 是定量讨论单组分体系两相平衡问题的理论基础, 其正确性已被实验、实践充分证明[4-6]。热力学第二定律成立以后, 人们用热力学方法推导出适用于纯物质封闭系统在任意温度 T(p)下, 任意两相的平衡的Clapeyron 方程。以下是现行大多物理化学教材对该方程的推导方法：

在T，p时某纯物质(单组分体系)达到两相平衡(用1，2分别表示两个相)，则:

G1=G2

(1)

若温度改变dT，相应地压力改变dp, 由此引起吉布斯自由能变化分别为dG1、dG2，变化后依然呈现两相平衡，即:

G1+dG1=G2+dG2

(2)

所以，

dG1=dG2

根据热力学基本公式

dG=-SdT+Vdp

(4)

得:

-S1dT+V1dP=-S2dT+V2dp

(5)

即，

(6)

所以，

(8)

(8)式即为著名的Clapeyron 方程，若发生变化的物质的量取1mol，则

(9)

如两相中有一相是气相(如气液平衡、气固平衡)，因为相同条件下，Vm(g)>>Vm(l)或Vm(s), △Vm≈Vm(g)，设气体为理想气体，则可代入理想气体状态方程，

(10)

即，

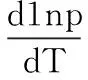
(11)

(11)式即为描述纯物质两相平衡体系压力与温度关系的Clausius-Clapeyron 方程。有文献指出, 由于两相平衡的单组分体系只有一个自由度, 即 T，p 中只能有一个独立变量，因此在(5) 式中多使用了一个自由度(T，p 均为独立变量), 存在着自变量使用不当的误解乃至争议[7-10]。文献[10]通过设计两步热力学过程对Clapeyorn方程的进行了推导，虽避免了独立变量的误解，但使问题复杂化了，不简明、不利于学生理解；文献[11]通过设计一个由两步可逆相变过程和两步等容可逆过程组成可逆循环，从可逆循环焓变和熵变导出了克拉贝龙方程，但推导过程比较繁琐，牵涉较多的计算与变换。

这里，我们介绍一个简单、严密的推导方法：

某纯物质达到两相平衡(用上标“1”、“2”分别表示两个相)，则在两相中的化学势相等，

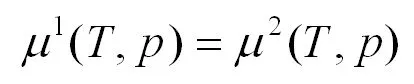
(12)

(13)

即，

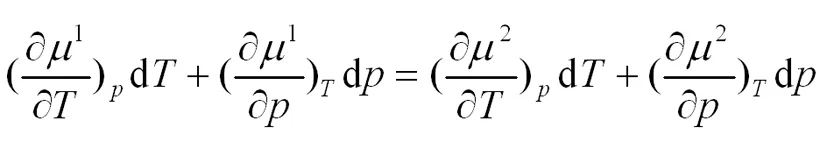
(14)由于

(15)

(16)

将上两式代入(14)式，

(17)

所以，

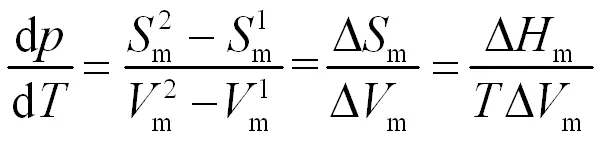
(18)

(18)式即Clapeyron 方程，上述(12)～(18)式的推导仅从数学多元函数微分的角度出发且过程简洁、明了、易懂，也不存在变量使用不当问题。此推导对教师教学和学生学习该公式有积极意义。

[1] 傅献彩,沈文霞,姚天扬，等. 物理化学[M]. 5版. 北京: 高等教育出版社, 2006.

[2] 天津大学物理化学教研室. 物理化学[M].4版. 北京: 高等教育出版社, 2001.

[3] 屈景年. 物理化学[M]. 北京: 中国人民大学出版社, 2009.

[4] 蒋风雷, 蔡雨萌, 邓立志, 等. 静态法和动态法测量乙醇饱和蒸气压的比较[J].大学化学, 2015, 30(4): 47-53.

[5] 王惠民. 液体在其正常沸点下的蒸发热计算[J].化学世界, 1993(2): 78-81.

[6] 王玉峰, 杜凤沛, 刘本才，等. 关于Clapeyron方程适用条件的讨论[J].大学化学, 2010, 25(2): 58-59.

[7] 郭余年, 赵凤云. 对公认的Clapeyron方程的推导的不同意见 [J].化学通报, 1995(11): 50-51.

[8] 郭余年, 朱毅瞥. 论如今公认的Clapeyron方程并非普遍成立之理由[J]. 化学通报, 1995(11): 52-53.

[10] 张常山, 俞柏恒, 叶静娴. Clapeyron方程推导的探讨[J]. 南京理工大学学报, 1999, 23(5): 474-476.

[11] 陈良坦, 蒋新征.利用循环法导出克拉贝龙方程 [J]. 大学化学, 2010, 25(4): 86-88.

(本文文献格式：刘兴,赖华,屈景年,等.关于Clapeyron方程推导的探讨[J].山东化工，2017，46(16)：171，173.)

Study on Deduction of Clapeyron Equation

Liu Xing*，Lai Hua，Qu Jingnian，Zeng Rongying，Li Junhua

(1 College of Chemistry and Material Science, Hengyang Normal University, Hengyang 421008, China)

Clapeyron equation is a significant equation in physical chemistry. In this paper, based on the point of multivariate function, a concise, rigorous method for deduction of Clapeyron equation is introduced. The present attempt is of great significance to learn and research this equation.

clapeyron equation；multivariate function；gas-liquid equilibrium；mathematics

O6-041

：A

：1008-021X(2017)16-0171-01

2017-05-23

衡阳师范学院教学改革研究项目(JYKT201512、JYKT201513)及湖南省自然科学基金项目(2016JJ6013).

刘 兴，湖南常宁人，博士、讲师，从事物理化学教学与研究。